hdu3739 Anti LIS[最小割]
长度为 n≤1000 的数列 ai,其中最长上升子序列的长度为 s。至少删去多少数使得最长上升子序列的长度小于 s。
其实这题和那个求有多少不重叠LIS是一样答案的.
先放个图。
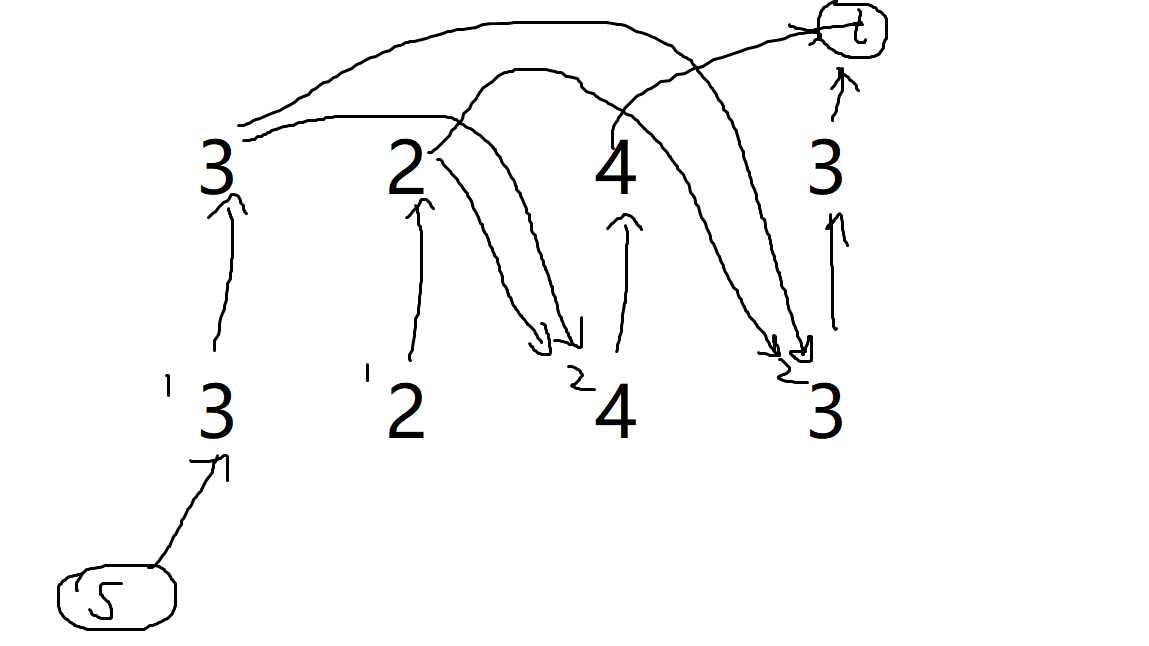
图丑别说我。
原网络的意思是从s到t是一条lis,那我们就对这个图进行破坏,求出一个最小割使它不连通即可。这里有几个问题。为什么是最小割?可以看出,删数操作就相当于把那个拆点间的边删掉,并且这种删法是最优的(看图想一想),比删入度,出度价值更少。那么就可以把删数想象为求最小割即最大流啦。最小割去掉后的数列不会再出现一个长s的lis吗?不会的,如果有,那删之前应该也是存在的,那就应该被删掉,与现在又出现矛盾,故不会出现。
1 #include<bits/stdc++.h> 2 using namespace std; 3 typedef long long ll; 4 typedef pair<int,int> pii; 5 template<typename T>inline char MIN(T&A,T B){return A>B?A=B,1:0;} 6 template<typename T>inline char MAX(T&A,T B){return A<B?A=B,1:0;} 7 template<typename T>inline T _min(T A,T B){return A<B?A:B;} 8 template<typename T>inline T _max(T A,T B){return A>B?A:B;} 9 template<typename T>inline T read(T&x){ 10 x=0;char c;while(!isdigit(c=getchar()))if(isalpha(c))return x=(int)c; 11 while(isdigit(c))x=(x<<1)+(x<<3)+(c^48),c=getchar();return x; 12 } 13 const int N=1000+7,M=500000+7,INF=0x3f3f3f3f; 14 int w[M<<1],v[M<<1],Next[M<<1],Head[N<<1],cur[N<<1],dis[N<<1],tot,s,t,n; 15 inline void Addedge(int x,int y,int z){ 16 v[++tot]=y,Next[tot]=Head[x],Head[x]=tot,w[tot]=z; 17 v[++tot]=x,Next[tot]=Head[y],Head[y]=tot,w[tot]=0; 18 } 19 #define y v[j] 20 inline char bfs(){ 21 queue<int> q;q.push(s),memset(dis,0,sizeof dis),dis[s]=1; 22 for(register int i=1;i<=(n<<1)+2;++i)cur[i]=Head[i]; 23 while(!q.empty()){ 24 int x=q.front();q.pop(); 25 for(register int j=Head[x];j;j=Next[j])if(w[j]&&!dis[y]){ 26 dis[y]=dis[x]+1,q.push(y); 27 if(y==t)return 1; 28 } 29 } 30 return 0; 31 } 32 int dinic(int x,int flow){ 33 if(!flow||x==t)return flow; 34 int rest=flow,k; 35 for(register int j=cur[x];j&&rest;cur[x]=j,j=Next[j])if(w[j]&&dis[y]==dis[x]+1){ 36 if(!(k=dinic(y,_min(rest,w[j]))))dis[y]=0; 37 rest-=k,w[j]-=k,w[j^1]+=k; 38 } 39 return flow-rest; 40 } 41 #undef y 42 int a[N],f[N],ans,maxflow,T; 43 44 int main(){//freopen("P2766.in","r",stdin);//freopen("P2766.txt","w",stdout); 45 read(T);while(T--){ 46 tot=1;read(n);s=(n<<1)+1,t=s+1,ans=maxflow=0; 47 memset(Head,0,sizeof Head); 48 for(register int i=1;i<=n;++i){ 49 read(a[i]);f[i]=1; 50 for(register int j=1;j<i;++j)if(a[j]<a[i])MAX(f[i],f[j]+1); 51 for(register int j=1;j<i;++j)if(a[j]<a[i]&&f[j]+1==f[i])Addedge(j+n,i,1); 52 MAX(ans,f[i]);Addedge(i,i+n,1);if(f[i]==1)Addedge(s,i,1); 53 } 54 for(register int i=1;i<=n;++i)if(f[i]==ans)Addedge(i+n,t,1); 55 while(bfs())maxflow+=dinic(s,INF); 56 printf("%d\n",maxflow); 57 } 58 return 0; 59 }

