#专题练习# 网络流
#最大流
#最大流建图#
#最小割建图#
最大和=全局和-舍弃和,而舍弃和=最小割=最大流。
有些时候,我们面临的选择过于复杂,要直接建图跑出最优解不太容易。这时候我们可以反向求解,画出流图,求最小割。图中总流量- 最小割= 最优解。
1. HDU 6598—— Harmonious Army
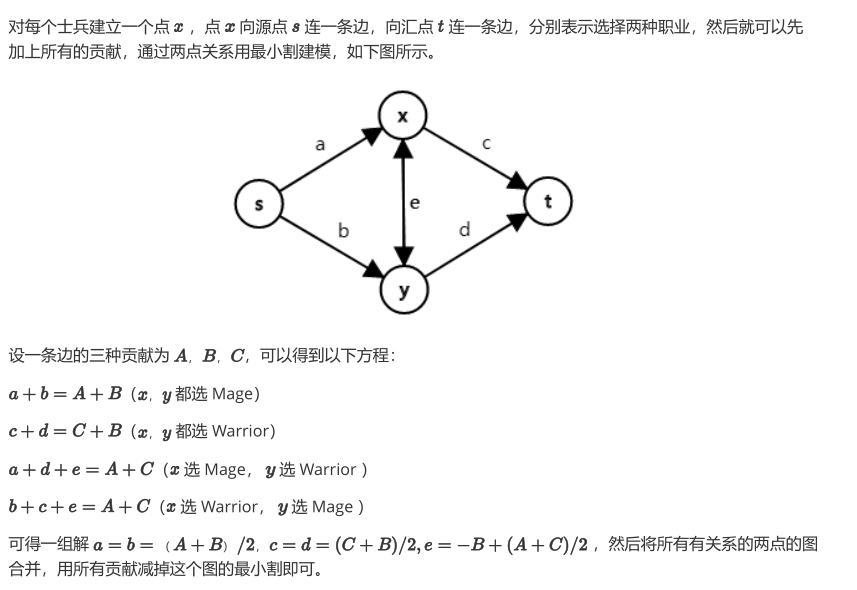
你是一个军队的将领,战争临近,你要操练你的士兵。你有N 个士兵,每个士兵可以在战士或法师里选择其中的一个职业。但是,对于某两个相识的人来说,他们的组合会产生不同的奇妙的结果。对于Xi 和 Xj 两名士兵,如果两个人都是战士,那么会产生a 数值的战斗力;如果两个人都是法师,会产生b (b= a/ 4+ c/ 3) 数值的战斗力;如果是战士+ 法师的搭配,则会产生c 点战斗力。现在给你N 个战士之间的关系和数值,你能帮将军计算出最优搭配下最大的战斗力吗?
Q:一眼看上去就像个最大流,然而......到最后都没把图建出来。
A:看了题解后醍醐灌顶,之前建图的时候一直执着于直接最大流跑出结果,没想到可以先求出最小割再减去的作法。
题目让我们在每个士兵的两种选择和可能导致的三种组队情况中,计算出可得的最大收益;换个思路其实就是让我们求出舍弃另外两种组队方式的最小损失。那么便是构出队内两个人之间战斗力的计算图,然后计算最小割求出两个低收益方案的和,然后从总收益和中减去这一部分。
+++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
有朋友问我上面的方程怎么来的?我第一次看题解的时候也卡住了,不过仔细一想就能发现上面的方程其实就是四种最小割的具体情况。
/* A:两个人都选择战士的收益;C:两个人都选择法师的收益;B:一战士一法师的收益 ;B= A/ 4+ C/ 3; */
/* a:士兵X做战士的收益;b:士兵X做法师的收益;c:士兵Y做战士的收益;d:士兵Y做法师的收益 */
对上图中的方程做一个解释:
我们要求上图的最小割,由我下面的证明可知:我们求得的每一个最小割都是相应情况下我们舍弃的两种低收益组合的收益和。故,
①最小割为a+ b:这种情况下a+ b< c+ d,图左半部分的流量小于右半部分。故我们选择了保留右半部分(两者都选择法师,保留了C),删掉左半部分使图不连通(两者都不做战士,这就同时丢掉了A和B)。故最小割(a+ b) 等于舍弃的收益A+ B。
②最小割为c+ d:这种情况下a+ b> c+ d,图左半部分的流量大于右半部分。故我们选择了保留左半部分(两者都选择战士,保留了A),删掉右半部分使图不连通(两者都不做法师,这就同时丢掉了C和B)。故最小割(c+ d) 等于舍弃的收益C+ B。
③最小割为a+ d+ e:这种情况下a+ e< b&& d+ e< c,即 a<<< c。图中的c 远远大于a。故我们选择了保留左半部分的b和右半部分的c (士兵X选择法师士兵Y选择战士,保留了B),删掉a, d, e使图不连通(士兵X不做战士Y不做法师,丢掉了A和C)。故最小割(a+ d+ e) 等于舍弃的收益A+ C。
④最小割为b+ c+ e:这种情况下b+ e< a&& c+ e< d,即 a>>> c。图中的a 远远大于c。故我们选择了保留左半部分的a和右半部分的d (士兵X选择战士士兵Y选择法师,保留了B),删掉b, c, e使图不连通(士兵X不做法师Y不做战士,丢掉了A和C)。故最小割(b+ c+ e) 等于舍弃的收益A+ C。
+++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
以求出最小割做减法求得最大收益的思路,我们进行分析:
图中总流量Sum= A+ B+ C;
①假设(x, y)两人都为战士收益最大,则可知A> C&& A> B;则我们求得的最小割的大小为S= min(A+ B,C+ B)= min(A, C)+ B= C+ B;,故而减去最小割得:Sum- S= A;为收益最大的组合。
②假设(x, y)两人都为法师收益最大,则可知C> A&& C> B;则我们求得的最小割的大小为S= min(A+ B,C+ B)= min(A, C)+ B= A+ B;,故而减去最小割得:Sum- S= C;为收益最大的组合。
③根据题目描述:B= A/ 4+ C/ 3;故不可能出现B> A&& B> C 的情况,故上两种情况恒成立。且因为(A+ C> A+ B|| A+ C> C+ B)恒为真,故上面的min()中可以忽略 (A+ C)。
综上所述,最小割思路符合题意。
1 /*建图*/ 2 scanf("%d %d", &n, &m); 3 int s= 0, t= n+ 1; 4 for (int i= 0; i< m; i ++) 5 { 6 /* 7 0 --> 源点 8 1~ n ---> n个士兵 9 n+ 1 ---> 汇点 10 */ 11 scanf("%d %d %lf %lf %lf", &u, &v, &a, &b, &c); 12 Add_ENode(s, u, (a+b)/2); 13 Add_ENode(s, v, (a+b)/2); 14 Add_ENode(u, t, (b+c)/2); 15 Add_ENode(v, t, (b+c)/2); 16 Add_ENode(u, v, -b+(a+c)/2); 17 Add_ENode(v, u, -b+(a+c)/2); 18 }
完整的代码在补题报告里:https://www.cnblogs.com/Amaris-diana/p/11228766.html
2.洛谷P2774—— 方格取数问题
题目描述
在一个有 m*n 个方格的棋盘中,每个方格中有一个正整数。现要从方格中取数,使任意 2 个数所在方格没有公共边,且取出的数的总和最大。试设计一个满足要求的取数算法。对于给定的方格棋盘,按照取数要求编程找出总和最大的数。
输入格式
第 1 行有 2 个正整数 m 和 n,分别表示棋盘的行数和列数。接下来的 m 行,每行有 n 个正整数,表示棋盘方格中的数。
输出格式
程序运行结束时,将取数的最大总和输出。
Q:题意很好理解。
A:同样是计算最小割再减去,不过建图时要仔细考虑。
+++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
首先根据题意给方格染色,给相邻的方格染上黑、白两种不同的颜色。
源点连向每一个黑色的点,流量为这个点的值;同理,每一个白色的点都连向汇点,流量为这个点的值。
每一个黑色的点都连向与它相临的白色的点,流量为INF。
最后,根据最小割最大流定理求得最小割;最大和= 全局和- 最小割求解。
+++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++

1 #include<algorithm> 2 #include<cstring> 3 #include<cstdio> 4 #include<queue> 5 using namespace std; 6 const int maxv= 510; 7 const int maxe= 60000; 8 const int INF= 0x3f3f3f3f; 9 struct ENode 10 { 11 int to; 12 int c; //容量; 13 int Next; 14 }; 15 ENode edegs[maxe]; 16 int Head[maxv], tnt; 17 void Add_ENode(int a, int b, int c) 18 { 19 /**建边*/ 20 edegs[++ tnt].to= b; 21 edegs[tnt].c= c; 22 edegs[tnt].Next= Head[a]; 23 Head[a]= tnt; 24 edegs[++ tnt].to= a; 25 edegs[tnt].c= 0; 26 edegs[tnt].Next= Head[b]; 27 Head[b]= tnt; 28 } 29 void into() 30 { 31 /**初始化*/ 32 memset(Head, -1, sizeof(Head)); 33 tnt= -1; 34 } 35 36 int level[maxv]; 37 bool bfs_level(int s, int t) 38 { 39 memset(level, 0, sizeof level); //所有点的等级初始化为-1; 40 level[s] = 1; //源点的等级为1; 41 queue<int> q; //队列que:按序保存已搜索到的点; 42 q.push(s); //先将源点s 加入队列; 43 44 while (!q.empty()) 45 { 46 int u = q.front(); //取出队首元素; 47 q.pop(); 48 for (int k = Head[u]; k!= -1; k = edegs[k].Next) 49 { 50 /*遍历,查找到之前未找到的、可抵达的点便加入队列*/ 51 int v = edegs[k].to; 52 if (level[v] || ! edegs[k].c) continue; 53 level[v] = level[u] + 1; //深度 +1; 54 q.push(v); 55 } 56 } 57 return level[t]; 58 } 59 60 int dfs(int now, int c_max, int t) 61 { 62 /**DFS 实现多路增广*/ 63 /*now:起点;c_max:从源点s到节点now的最大流量;t:汇点、dfs结束的终点*/ 64 if (now == t) return c_max; //当now== t时,c_max便是要求的最大流; 65 int ret = 0; 66 for (int k = Head[now]; c_max && k!= -1; k = edegs[k].Next) 67 { 68 int v = edegs[k].to; 69 if (level[v]== level[now]+ 1&& edegs[k].c) 70 { 71 int f = dfs(v, min(c_max, edegs[k].c), t); 72 edegs[k].c-= f; 73 edegs[k^ 1].c+= f; 74 ret+= f; 75 c_max-= f; 76 } 77 } 78 if (!ret) level[now] = 0; 79 return ret; 80 } 81 int dinic(int s, int t) 82 { 83 int ret = 0; 84 while (bfs_level(s, t)) 85 { 86 ret += dfs(s, INF, t); 87 } 88 return ret; 89 } 90 91 int detx[4]= {1, -1, 0, 0}; 92 int dety[4]= {0, 0, 1, -1}; 93 int main() 94 { 95 int n, m; 96 int w; 97 scanf("%d %d", &n, &m); 98 int s= 0, t= n* m+ 1; 99 into(); 100 int sum= 0; 101 for (int i= 1; i<= n; i ++) 102 { 103 for (int j= 1; j<= m; j ++) 104 { 105 int p= (i- 1)* m+ j; 106 scanf("%d", &w); 107 sum+= w; 108 if ((i+ j)% 2== 1) Add_ENode(s, p, w); 109 else Add_ENode(p, t, w); 110 } 111 } 112 for (int i= 1; i<= n; i ++) 113 { 114 for (int j= 1; j<= m; j ++) 115 { 116 if ((i+ j)% 2== 0) continue; 117 int p= (i- 1)* m+ j; 118 for (int k= 0; k< 4; k ++) 119 { 120 int nx= i+ detx[k]; 121 int ny= j+ dety[k]; 122 if (nx< 1|| nx> n|| ny< 1|| ny> m) continue; 123 int np= (nx- 1)* m+ ny; 124 Add_ENode(p, np, INF); 125 } 126 } 127 } 128 int answer= dinic(s, t); 129 sum-= answer; 130 printf("%d\n", sum); 131 return 0; 132 }
#二分图匹配#
1. 洛谷 P2756 飞行员配对方案问题
题目描述
英国皇家空军从沦陷国征募了大量外籍飞行员。由皇家空军派出的每一架飞机都需要配备在航行技能和语言上能互相配合的2 名飞行员,其中1 名是英国飞行员,另1名是外籍飞行员。在众多的飞行员中,每一名外籍飞行员都可以与其他若干名英国飞行员很好地配合。如何选择配对飞行的飞行员才能使一次派出最多的飞机。对于给定的外籍飞行员与英国飞行员的配合情况,试设计一个算法找出最佳飞行员配对方案,使皇家空军一次能派出最多的飞机。
对于给定的外籍飞行员与英国飞行员的配合情况,编程找出一个最佳飞行员配对方案,使皇家空军一次能派出最多的飞机。
输入格式
第 1 行有 2 个正整数 m 和 n。n 是皇家空军的飞行员总数(n<100);m 是外籍飞行员数(m<=n)。外籍飞行员编号为 1~m;英国飞行员编号为 m+1~n。
接下来每行有 2 个正整数 i 和 j,表示外籍飞行员 i 可以和英国飞行员 j 配合。最后以 2个" -1" 结束。
输出格式
第 1 行是最佳飞行员配对方案一次能派出的最多的飞机数 M。接下来 M 行是最佳飞行员配对方案。每行有 2个正整数 i 和 j,表示在最佳飞行员配对方案中,飞行员 i 和飞行员 j 配对。如果所求的最佳飞行员配对方案不存在,则输出‘No Solution!’。
Q:有N名飞行员,其中M名为外籍飞行员,剩下的都为英国飞行员。每一架飞机都要求一个外籍+一位英国飞行员搭档驾驶,现给出可能的人员搭配,问你最多能找到有多少组合法的组合?
A:一个模板式的二分图匹配,唯一例外的就是需要额外输出配对的组合;但这并不麻烦,只要遍历每一个 外籍飞行员->英国飞行员 的单向边,边的容量小于初值的便是我们要找的一对组合。

1 #include<algorithm> 2 #include<cstring> 3 #include<cstdio> 4 #include<queue> 5 using namespace std; 6 const int maxv= 510; 7 const int maxe= 60000; 8 const int INF= 0x3f3f3f3f; 9 struct ENode 10 { 11 int to; 12 int c; //容量; 13 int Next; 14 }; 15 ENode edegs[maxe]; 16 int Head[maxv], tnt; 17 void Add_ENode(int a, int b, int c) 18 { 19 /**建边*/ 20 edegs[++ tnt].to= b; 21 edegs[tnt].c= c; 22 edegs[tnt].Next= Head[a]; 23 Head[a]= tnt; 24 edegs[++ tnt].to= a; 25 edegs[tnt].c= 0; 26 edegs[tnt].Next= Head[b]; 27 Head[b]= tnt; 28 } 29 void into() 30 { 31 /**初始化*/ 32 memset(Head, -1, sizeof(Head)); 33 tnt= -1; 34 } 35 36 int level[maxv]; 37 bool bfs_level(int s, int t) 38 { 39 memset(level, 0, sizeof level); //所有点的等级初始化为-1; 40 level[s] = 1; //源点的等级为1; 41 queue<int> q; //队列que:按序保存已搜索到的点; 42 q.push(s); //先将源点s 加入队列; 43 44 while (!q.empty()) 45 { 46 int u = q.front(); //取出队首元素; 47 q.pop(); 48 for (int k = Head[u]; k!= -1; k = edegs[k].Next) 49 { 50 /*遍历,查找到之前未找到的、可抵达的点便加入队列*/ 51 int v = edegs[k].to; 52 if (level[v] || ! edegs[k].c) continue; 53 level[v] = level[u] + 1; //深度 +1; 54 q.push(v); 55 } 56 } 57 return level[t]; 58 } 59 60 int dfs(int now, int c_max, int t) 61 { 62 /**DFS 实现多路增广*/ 63 /*now:起点;c_max:从源点s到节点now的最大流量;t:汇点、dfs结束的终点*/ 64 if (now == t) return c_max; //当now== t时,c_max便是要求的最大流; 65 int ret = 0; 66 for (int k = Head[now]; c_max && k!= -1; k = edegs[k].Next) 67 { 68 int v = edegs[k].to; 69 if (level[v]== level[now]+ 1&& edegs[k].c) 70 { 71 int f = dfs(v, min(c_max, edegs[k].c), t); 72 edegs[k].c-= f; 73 edegs[k^ 1].c+= f; 74 ret+= f; 75 c_max-= f; 76 } 77 } 78 if (!ret) level[now] = 0; 79 return ret; 80 } 81 int dinic(int s, int t) 82 { 83 int ret = 0; 84 while (bfs_level(s, t)) 85 { 86 ret += dfs(s, INF, t); 87 } 88 return ret; 89 } 90 91 int main() 92 { 93 int n, m; 94 scanf("%d %d", &m, &n); 95 int s= 0, t= n+ m+ 1; 96 into(); 97 for (int i= 1; i<= m; i ++) 98 { 99 Add_ENode(s, i, 1); 100 } 101 for (int i= m+ 1; i<= n; i ++) 102 { 103 Add_ENode(i, t, 1); 104 } 105 int a, b; 106 while (~ scanf("%d %d", &a, &b)) 107 { 108 if (a== -1&& b== -1) break; 109 if (a> b) swap(a, b); 110 Add_ENode(a, b, INF); 111 } 112 int answer= dinic(s, t); 113 printf("%d\n", answer); 114 for (int i= 1; i<= m; i ++) 115 { 116 for (int k = Head[i]; k!= -1; k = edegs[k].Next) 117 { 118 int v = edegs[k].to; 119 // printf("--> %d %d %d\n", i, v, edegs[k].c); 120 if (v!= s&& edegs[k].c!= INF) 121 { 122 printf("%d %d\n", i, v); 123 } 124 } 125 } 126 /*输出结果*/ 127 return 0; 128 }
end;






