2019暑假杭电训练赛(补题及笔记)
第一场
1005.Path
多年后,杰瑞爱上了一个女孩,他经常走很长时间去看望她。但是,因为他花太多的时间和他的女朋友在一起,汤姆觉得被忽视了,想阻止他去看她。经过对小区的研究,Tom发现小区正好由n栋房屋组成,其中一些房屋与直路相连。去看望他的女朋友,杰瑞需要从他的房子1开始,沿着最短路径,到达n。现在汤姆想要阻碍一些道路,使杰瑞走更长的时间到达女孩的家中,他发现阻塞道路的成本等于它的长度。现在他想知道使杰里走得更长所需的最低总成本。注意,如果Jerry一开始不能到他女朋友家,答案显然是零。而且你不需要保证在堵住了一些边之后,仍然有一条路从杰里的家到他女朋友的家。
Q:用最短的花费使最短路径变成。
A:实际上就是要找到所有可能的最短路径,然后做最小割。首先,求出最短路径,然后遍历边集,找到所有 Dis[v]== Dis[u]+ cost的边,构建一个图G'(用于求最大流的图,记得建回退边)。然后跑最大流得到结果(一个图的最小割等于这个图的最大流)。【代码:侯曜辉】

1 #include<algorithm> 2 #include<iostream> 3 #include<cstring> 4 #include<cstdio> 5 #include<queue> 6 using namespace std; 7 typedef long long LL; 8 const int maxv= 10010; 9 const int maxe= 40010; 10 const LL inf= 0x3f3f3f3f3f3f3f3f; 11 12 struct ENode 13 { 14 int from; 15 int to; 16 LL w; 17 int Next; 18 }; 19 ENode edegs[maxe]; 20 int Head[maxv], tnt; 21 void init() 22 { 23 memset(Head, -1, sizeof(Head)); 24 tnt= -1; 25 } 26 void Add_ENode(int a, int b, LL w) 27 { 28 ++ tnt; 29 edegs[tnt].from= a; 30 edegs[tnt].to= b; 31 edegs[tnt].w= w; 32 edegs[tnt].Next= Head[a]; 33 Head[a]= tnt; 34 } 35 36 LL dis[maxv]; 37 struct cmpx 38 { 39 bool operator() (int &a, int &b) const 40 { 41 return dis[a]- dis[b]> 0; 42 } 43 }; 44 void Dijkstra(int x) 45 { 46 priority_queue<int, vector<int>, cmpx> q; 47 memset(dis, inf, sizeof(dis)); 48 dis[x]= 0; 49 q.push(x); 50 51 while (! q.empty()) 52 { 53 int u= q.top(); 54 q.pop(); 55 56 for (int k= Head[u]; k!= -1; k= edegs[k].Next) 57 { 58 int v= edegs[k].to; 59 if (dis[v]> dis[u]+ edegs[k].w ) 60 { 61 dis[v]= dis[u]+ edegs[k].w; 62 q.push(v); 63 } 64 } 65 } 66 } 67 68 /*建新图,跑最大流*/ 69 ENode edegs1[maxe]; 70 int Head1[maxv], tnt1; 71 void init1() 72 { 73 memset(Head1, -1, sizeof(Head1)); 74 tnt1= -1; 75 } 76 void Add_ENode1(int a, int b,LL w) 77 { 78 ++ tnt1; 79 edegs1[tnt1].from= a; 80 edegs1[tnt1].to= b; 81 edegs1[tnt1].w= w; 82 edegs1[tnt1].Next= Head1[a]; 83 Head1[a]= tnt1; 84 ++ tnt1; 85 edegs1[tnt1].from= b; 86 edegs1[tnt1].to= a; 87 edegs1[tnt1].w= 0; 88 edegs1[tnt1].Next= Head1[b]; 89 Head1[b]= tnt1; 90 } 91 void Dijk2(int n) 92 { 93 init1(); 94 for (int u= 1; u<= n; u ++) 95 { 96 for (int k= Head[u]; k!= -1; k= edegs[k].Next) 97 { 98 int v= edegs[k].to; 99 if (dis[v]== dis[u]+ edegs[k].w ) 100 { 101 Add_ENode1(u, v, edegs[k].w); 102 } 103 } 104 } 105 } 106 int level[maxv]; 107 bool bfs_level (int s, int t) 108 { 109 memset(level, -1, sizeof(level)); //所有点的等级初始化为-1; 110 level[s]= 1; //源点的等级为1; 111 int que[maxv]; //队列que:按序保存已搜索到的点; 112 int iq= 0; 113 que[iq ++]= s; //先将源点s 加入队列; 114 for (int i= 0; i< iq; i ++) 115 { 116 int u= que[i]; //取出队首元素; 117 if (u== t) 118 { 119 /*找到汇点t,返回*/ 120 return true; 121 } 122 for (int k= Head1[u]; k!= -1; k= edegs1[k].Next) 123 { 124 /*遍历,查找到之前未找到的、可抵达的点便加入队列*/ 125 int v= edegs1[k].to; 126 if (-1== level[v]&& edegs1[k].w) 127 { 128 level[v]= level[u]+ 1; //深度 +1; 129 que[iq ++]= v; 130 } 131 } 132 } 133 return false; 134 } 135 LL dfs(int now, LL c_max, int t) 136 { 137 /**DFS 实现多路增广*/ 138 /*now:起点;c_max:从源点s到节点now的最大流量;t:汇点、dfs结束的终点*/ 139 if (now== t) return c_max; //当now== t时,c_max便是要求的最大流; 140 LL ret= 0, f; 141 for (int k= Head1[now]; k!= -1; k= edegs1[k].Next) 142 { 143 if (edegs1[k].w&& level[edegs1[k] .to]== level[now]+ 1) 144 { 145 /**/ 146 f= dfs(edegs1[k].to, min(c_max- ret, edegs1[k].w), t); 147 edegs1[k].w-= f; 148 edegs1[k^1].w+= f; 149 ret+= f; 150 if(ret== c_max) return ret; 151 } 152 } 153 return ret; 154 } 155 LL dinic(int s, int t) 156 { 157 LL ans= 0; 158 while(bfs_level(s, t)) 159 { 160 ans+= dfs(s, inf, t); 161 } 162 return ans; 163 } 164 165 int main() 166 { 167 int t; 168 int n, m; 169 scanf("%d", &t); 170 while (t --) 171 { 172 scanf("%d %d", &n, &m); 173 init(); 174 int a, b; 175 LL w; 176 for (int i= 0; i< m; i ++) 177 { 178 scanf("%d %d %lld", &a, &b, &w); 179 Add_ENode(a, b, w); 180 } 181 int start= 1, endd= n; 182 // scanf("%d %d", &start, &endd); 183 Dijkstra(start); 184 LL ans; 185 if (dis[n]== inf) ans= 0; 186 else 187 { 188 Dijk2(n); 189 // cout << dis[n] << " " << tnt1 << endl; 190 // for (int i= 0; i<= tnt1; i ++) 191 // { 192 // cout << edegs1[i].from << "--->" << edegs1[i].to << "--->" << edegs1[i].w << endl; 193 // } 194 ans= dinic(start, endd); 195 } 196 197 printf("%lld\n", ans); 198 } 199 return 0; 200 }
1002.
第二场
1008. Harmonious Army —— HDU 6598
你是一个军队的将领,战争临近,你要操练你的士兵。你有N 个士兵,每个士兵可以在战士或法师里选择其中的一个职业。但是,对于某两个相识的人来说,他们的组合会产生不同的奇妙的结果。对于Xi 和 Xj 两名士兵,如果两个人都是战士,那么会产生a 数值的战斗力;如果两个人都是法师,会产生b (b= a/ 4+ c/ 3) 数值的战斗力;如果是战士+ 法师的搭配,则会产生c 点战斗力。现在给你N 个战士之间的关系和数值,你能帮将军计算出最优搭配下最大的战斗力吗?
Q:一眼看上去就像个最大流,然而......到最后都没把图建出来。
A:看了题解后醍醐灌顶,之前建图的时候一直执着于直接最大流跑出结果,没有反向思考这种先求出最小割然后再减去得到结果的作法。这道题让我们在每个士兵的两种选择和可能导致的三种组队情况中,计算出可得的最大收益;换个思路其实就是让我们求出舍弃另外两种组队方式的最小损失。那么便是构出队内两个人之间战斗力的计算图,然后计算最小割,然后从总收益和中减去这一部分。
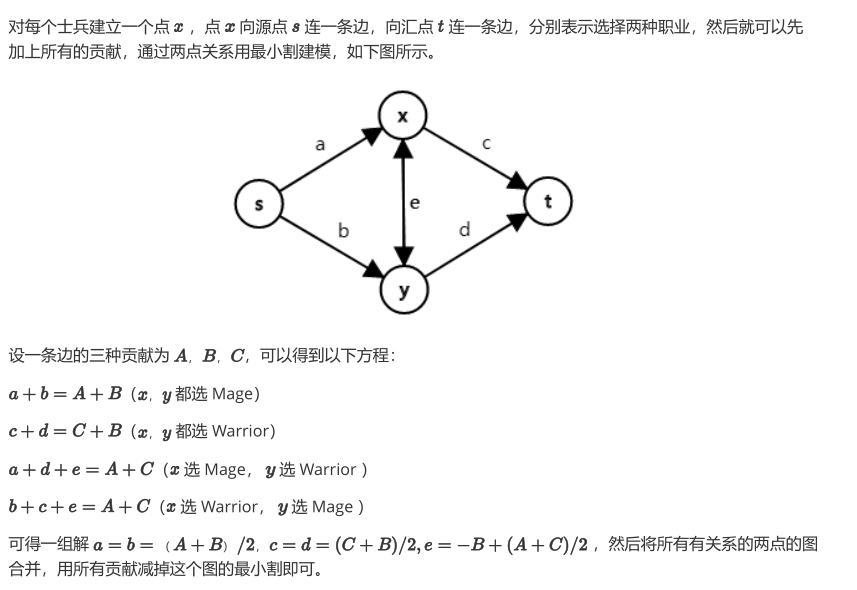
+++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
有朋友问我上面的方程怎么来的?我第一次看题解的时候也卡住了,不过仔细一想就能发现上面的方程其实就是四种最小割的具体情况。
/* A:两个人都选择战士的收益;C:两个人都选择法师的收益;B:一战士一法师的收益 ;B= A/ 4+ C/ 3; */
/* a:士兵X做战士的收益;b:士兵X做法师的收益;c:士兵Y做战士的收益;d:士兵Y做法师的收益 */
对上图中的方程做一个解释:
我们要求上图的最小割,由我下面的证明可知:我们求得的每一个最小割都是相应情况下我们舍弃的两种低收益组合的收益和。故,
①最小割为a+ b:这种情况下a+ b< c+ d,图左半部分的流量小于右半部分。故我们选择了保留右半部分(两者都选择法师,保留了C),删掉左半部分使图不连通(两者都不做战士,这就同时丢掉了A和B)。故最小割(a+ b) 等于舍弃的收益A+ B。
②最小割为c+ d:这种情况下a+ b> c+ d,图左半部分的流量大于右半部分。故我们选择了保留左半部分(两者都选择战士,保留了A),删掉右半部分使图不连通(两者都不做法师,这就同时丢掉了C和B)。故最小割(c+ d) 等于舍弃的收益C+ B。
③最小割为a+ d+ e:这种情况下a+ e< b&& d+ e< c,即 a<<< c。图中的c 远远大于a。故我们选择了保留左半部分的b和右半部分的c (士兵X选择法师士兵Y选择战士,保留了B),删掉a, d, e使图不连通(士兵X不做战士Y不做法师,丢掉了A和C)。故最小割(a+ d+ e) 等于舍弃的收益A+ C。
④最小割为b+ c+ e:这种情况下b+ e< a&& c+ e< d,即 a>>> c。图中的a 远远大于c。故我们选择了保留左半部分的a和右半部分的d (士兵X选择战士士兵Y选择法师,保留了B),删掉b, c, e使图不连通(士兵X不做法师Y不做战士,丢掉了A和C)。故最小割(b+ c+ e) 等于舍弃的收益A+ C。
+++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
以求出最小割做减法求得最大收益的思路,我们进行分析:
Sum= A+ B+ C;
①假设(x, y)两人都为战士收益最大,则可知A> C&& A> B;则我们求得的最小割的大小为S= min(A+ B,C+ B)= min(A, C)+ B= C+ B;,故而减去最小割得:Sum- S= A;为收益最大的组合。
②假设(x, y)两人都为法师收益最大,则可知C> A&& C> B;则我们求得的最小割的大小为S= min(A+ B,C+ B)= min(A, C)+ B= A+ B;,故而减去最小割得:Sum- S= C;为收益最大的组合。
③根据题目描述:B= A/ 4+ C/ 3;故不可能出现B> A&& B> C 的情况,故上两种情况恒成立。且因为(A+ C> A+ B|| A+ C> C+ B)恒为真,故上面的min()中可以忽略 (A+ C)。
综上所述,最小割思路符合题意。
(唯一要槽的就是——为什么链式前向星存图数组没开够在hduoj反馈的错误会是TLE啊真是跪了orz, 找了一个小时问题心都碎了)

1 #include<algorithm> 2 #include<cstring> 3 #include<cstdio> 4 using namespace std; 5 const int MAX_V= 510; 6 const int MAX_E= 4000000; 7 const double INF= 99999999999.000; 8 struct ENode 9 { 10 int to; 11 double c; //容量; 12 int Next; 13 }; 14 ENode edegs[MAX_E]; 15 int Head[MAX_V], tnt; 16 void Add_ENode(int a, int b, double c) 17 { 18 /**建边*/ 19 edegs[++ tnt].to= b; 20 edegs[tnt].c= c; 21 edegs[tnt].Next= Head[a]; 22 Head[a]= tnt; 23 edegs[++ tnt].to= a; 24 edegs[tnt].c= 0; 25 edegs[tnt].Next= Head[b]; 26 Head[b]= tnt; 27 } 28 void into() 29 { 30 /**初始化*/ 31 memset(Head, -1, sizeof(Head)); 32 tnt= -1; 33 } 34 35 int level[MAX_V]; 36 bool bfs_level (int s, int t) 37 { 38 memset(level, -1, sizeof(level)); //所有点的等级初始化为-1; 39 level[s]= 1; //源点的等级为1; 40 int que[MAX_V]; //队列que:按序保存已搜索到的点; 41 int iq= 0; 42 que[iq ++]= s; //先将源点s 加入队列; 43 for (int i= 0; i< iq; i ++) 44 { 45 int u= que[i]; //取出队首元素; 46 if (u== t) 47 { 48 /*找到汇点t,返回*/ 49 return true; 50 } 51 for (int k= Head[u]; k!= -1; k= edegs[k].Next) 52 { 53 /*遍历,查找到之前未找到的、可抵达的点便加入队列*/ 54 int v= edegs[k].to; 55 if (-1== level[v]&& 0< edegs[k].c) 56 { 57 level[v]= level[u]+ 1; //深度 +1; 58 que[iq ++]= v; 59 } 60 } 61 } 62 return false; 63 } 64 double dfs(int now, double c_max, int t) 65 { 66 /**DFS 实现多路增广*/ 67 /*now:起点;c_max:从源点s到节点now的最大流量;t:汇点、dfs结束的终点*/ 68 if (now== t) return c_max; //当now== t时,c_max便是要求的最大流; 69 double ret= 0, f; 70 for (int k= Head[now]; k!= -1; k= edegs[k].Next) 71 { 72 if (0< edegs[k].c&& level[edegs[k] .to]== level[now]+ 1) 73 { 74 /**/ 75 f= dfs(edegs[k].to, min(c_max- ret, edegs[k].c), t); 76 edegs[k].c-= f; 77 edegs[k^1].c+= f; 78 ret+= f; 79 if(ret== c_max) return ret; 80 } 81 } 82 return ret; 83 } 84 double dinic(int s, int t) 85 { 86 double ans= 0; 87 while(bfs_level(s, t)) 88 { 89 ans+= dfs(s, INF, t); 90 } 91 return ans; 92 } 93 94 int main() 95 { 96 int n, m; 97 int u, v; 98 double a, b, c; 99 while(~ scanf("%d %d", &n, &m)) 100 { 101 into(); 102 double sum= 0; 103 int s= 0; 104 int t= n+ 1; 105 for (int i= 0; i< m; i ++) 106 { 107 /* 108 0 --> 源点 109 1~ n ---> n个士兵 110 n+ 1 ---> 汇点 111 */ 112 scanf("%d %d %lf %lf %lf", &u, &v, &a, &b, &c); 113 sum += a; 114 sum += b; 115 sum += c; 116 /*士兵之间建流量为无限的双向边*/ 117 Add_ENode(s, u, (a+b)/2); 118 Add_ENode(s, v, (a+b)/2); 119 Add_ENode(u, t, (b+c)/2); 120 Add_ENode(v, t, (b+c)/2); 121 Add_ENode(u, v, -b+(a+c)/2); 122 Add_ENode(v, u, -b+(a+c)/2); 123 } 124 double answer= dinic(s, t); 125 long long ans= (long long)sum- answer; 126 printf("%lld\n", ans); 127 /*输出结果*/ 128 } 129 return 0; 130 }
end;






