计算几何——认识基本object:点、线、面 。
认识基本object:点、线、面
一、点
点用P(x, y)来表示;如:
1 typedef pair<double, double> _pair; 2 _pair point[MAXN];
二、线
①两点式
L: (y- y1)/ (y2- y1)= (x- x1)/ (x2- x1).
需要条件:用于已知两点坐标的情况。P1(x1, y1); P2(x2, y2);
在使用上几乎没有什么缺点。
1 typedef pair<double, double> _pair; 2 _pair point[MAXN]; 3 typedef pair<_pair, _pair> _line; 4 /*两点确定一条直线; _pair P1; _pair P2;*/ 5 _line Line[MAXN];
②斜截式
L: y= kx+ b;
需要条件:用于已知斜率和y轴截距。k; b;
优点:能够简单 快速&直观 的推出关系式,如计算两条直线交点。
缺点:一些特殊情况不适用,如当k 不存在时。
③点斜式
L: y- y1= k(x- x1);
需要条件:用于已知斜率和一点坐标的情况。k; P1(x1, y1);
缺点:同样依赖于斜率,当斜率不存在时不适用。
④截距式
L: (x/ a)+ (y/ b)= 1;
需要条件:用于已知所有截距的情况。x轴截距a; y轴截距b;
⑤一般式
L: ax+ by+ c= 0;
缺点:除了求交点或点到直线距离,其他方面都是缺点。不推荐使用。
三、面
1、圆
用圆心O(x, y)和半径R 来表示
1 typedef pair<double, double> _pair; 2 _pair point[MAXN]; 3 typedef pair<_pair, double> _round; 4 /*圆心_pair O; 半径double R*/ 5 _round Round[MAXN];
2、半平面 (待填)
用一个向量来表示 半平面,向量逆时针的方向为半平面的内部。
1 typedef pair<double, double> _pair; 2 typedef pair<_pair, _pair> _line; 3 /*确定一条向量; 向量OP:_pair O; _pair P;*/
Ps:平面内的一条直线把这个平面分成两部分,每一部分对这个平面来说,都叫做半平面。包括这条直线的半平面叫做闭半平面,否则叫做开半平面。
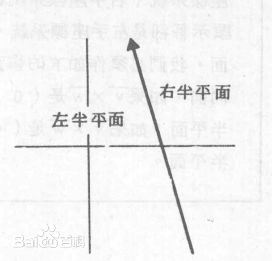
Ps: 一般的,我们默认向量的逆时针方向为半平面的内部。上图中即为向量的左半平面。
end;





