图论其一：图的存储

图的存储

　　图的存储大致分为三类：邻接矩阵，前向星，邻接表。

 

邻接矩阵

　　邻接矩阵是表示图的数据结构中最简单也是最常用的一种，对于一个有N个点的图，建立一个N* N的矩阵，这个矩阵的第i 行第j 列的值表示V_i 到V_j 的距离。

　　邻接矩阵需要初始化，map[i ][i ]= 0, map[i ][j ]= inf。对每组输入的V_i ，V_j 和 W_ij ，赋值为map[i ][j ]= W_ij 。

   

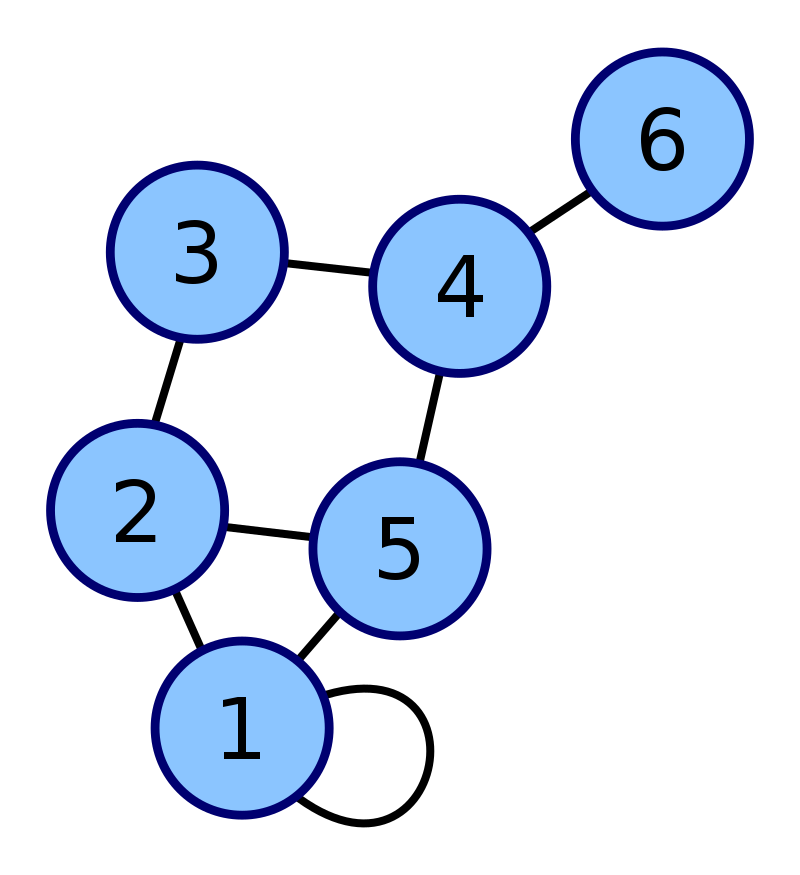
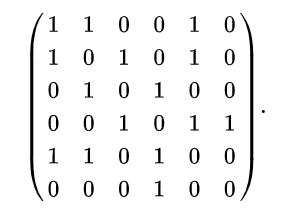
【图源维基百科】

　　上图中两点间有边连接则为1 ，否则为0 。无向图中不用考虑边的方向。

　　对于一个N个点，M条边的图，邻接矩阵的初始化需要O(N²)的时间，建图需要O(M)的时间；总的时间复杂度是O(N²)，空间复杂度也是O(N²)。

　　邻接矩阵的优点是实现简单，可以直接查询两点之间是否有边和边的权值；缺点是遍历效率极低，并且不能储存重边；初始化效率低；当N比较大时(>=1E+5)，建一个邻接矩阵的思路是不现实的；且对于稀疏图(E< N*logN)，邻接矩阵的空间利用效率不高，会造成大量浪费。

 

 

前向星

　　前向星的构造方式非常简单，读入每条边的信息^①，将边存放在数组中^②，把数组中的边按照起点顺序排序^③，前向星就构造完成了。为了查询方便，常用一个数组存储起点为V_i 的第一条边的位置。

　　①存储结构和比较函数

const int maxn= 1E+5;

struct Node
{
    int from;       //起点;
    int to;         //终点;
    int w;          //权;
};
bool cmpx (Node a, Node b)
{
    if (a.from== b.from&& a.to== b.to) return a.w- b.w< 0;
    if (a.from== b.from) return a.to- b.to< 0;
    return a.from- b.from< 0;
}
Node ENode[maxn];   //边集;
int Head[maxn];     //记录每个起点的第一条边的位置;

Node类型用来保存边；所有的边都存放进ENode[ ]中；Head[ ]存储从V_i 出发的第一条边的地址；cmpx按照 from> to> w 的优先级， 以从小到大的顺序对ENode[ ]里的边排序；

　　②数据输入

    int n, m;
    cin >>n >>m;
    int a, b, w;
    //有向图建图;
    for (int i = 0; i < m; i ++)
    {
        cin >>a >>b >>w;
        ENode[i].from= a;
        ENode[i].to= b;
        ENode[i].w= w;
    }
    sort(ENode, ENode+ m, cmpx);
    memset(Head, -1, sizeof(Head));//如果一个点出发没有边的话,Head[]= -1;
    Head[ENode[0].from ]= 0;
    for (int i = 1; i < m; i ++)
    {
        if (ENode[i].from!= ENode[i- 1].from ) Head[ENode[i].from ]= i;
    }

要注意的是，无向图时，一条边需要保存两边；

    int n, m;
    cin >>n >>m;
    int a, b, w;
    //无向图建图;
    for (int i = 0; i < m* 2; i ++)
    {
        cin >>a >>b >>w;
        ENode[i].from= a;
        ENode[i].to= b;
        ENode[i].w= w;
        ++ i;       //无向图需要存两次边,各自从一个起点出发;
        ENode[i].from= b;
        ENode[i].to= a;
        ENode[i].w= w;
    }
    sort(ENode, ENode+ m*2, cmpx);
    memset(Head, -1, sizeof(Head));//如果一个点出发没有边的话,Head[]= -1;
    Head[ENode[0].from ]= 0;
    for (int i = 1; i < m* 2; i ++)
    {
        if (ENode[i].from!= ENode[i- 1].from ) Head[ENode[i].from ]= i;
    }

 

　　③遍历

    for (int j= 1; j <= n; j ++) //从编号为1 的点开始;
    {
        for (int k= Head[j]; ENode[k].from== j&& k< m; k ++)
        {
            cout <<k <<":" <<ENode[k].from <<" " <<ENode[k].to <<" " <<ENode[k].w <<endl;
        }
    }

注意无向图的边数是m* 2；

    //遍历;
    for (int j= 1; j <= n; j ++) //从编号为1 的点开始;
    {
        for (int k= Head[j]; ENode[k].from== j&& k< m* 2; k ++)
        {
            cout <<k <<":" <<ENode[k].from <<" " <<ENode[k].to <<" " <<ENode[k].w <<endl;
        }
    }

 

然后我们来举个例子，以下面的数据为例：

5 5
1 2 4
1 3 5
1 4 6
1 5 7
2 3 8

我们来做一些修改，将无向图遍历代码改为：

    //遍历;
    for (int j= 1; j <= n; j ++) //从编号为1 的点开始;
    {
        cout <<j <<": ";
        for (int k= Head[j]; ENode[k].from== j&& k< m* 2; k ++)
        {
            cout <<"-->" <<ENode[k].to <<" ";
        }
        cout << endl;
    }

我们会看到：

我们能看到，对于从1 这个点出发的每一条边，都按照终点的大小从小到大排序了；

 由于涉及排序，所以前向星的构造时间复杂度与使用的排序算法有关，一般情况下时间复杂度为O(M*logM)，空间复杂度为O(M+N)；

前向星的优点在于可以应对非常多的情况，可以存储重边；但缺点在于不能直接判断任意两点间是否有边，而且排序需要浪费一些时间。

 ps：对于判断两点间是否存在边的问题，个人认为，由于前向星对从V_i 出发的每一条边都按照终点进行了排序，故可以使用二分进行查找；

#include<iostream>
#include<algorithm>
#include<cstdio>
#include<cstring>
using namespace std;
const int maxn= 1E+5;

struct Node
{
    int from;       //起点;
    int to;         //终点;
    int w;          //权;
};
bool cmpx (Node a, Node b)
{
    if (a.from== b.from&& a.to== b.to) return a.w- b.w< 0;
    if (a.from== b.from) return a.to- b.to< 0;
    return a.from- b.from< 0;
}
Node ENode[maxn];   //边集;
int Head[maxn];     //记录每个起点的第一条边的位置;
int main()
{
    int n, m;
    cin >>n >>m;
    int a, b, w;
    //无向图建图;
    for (int i = 0; i < m* 2; i ++)
    {
        cin >>a >>b >>w;
        ENode[i].from= a;
        ENode[i].to= b;
        ENode[i].w= w;
        ++ i;       //无向图需要存两次边,各自从一个起点出发;
        ENode[i].from= b;
        ENode[i].to= a;
        ENode[i].w= w;
    }
    sort(ENode, ENode+ m*2, cmpx);
    memset(Head, -1, sizeof(Head));//如果一个点出发没有边的话,Head[]= -1;
    Head[ENode[0].from ]= 0;
    for (int i = 1; i < m* 2; i ++)
    {
        if (ENode[i].from!= ENode[i- 1].from ) Head[ENode[i].from ]= i;
    }
    //遍历;
    for (int j= 1; j <= n; j ++) //从编号为1 的点开始;
    {
        for (int k= Head[j]; ENode[k].from== j&& k< m* 2; k ++)
        {
            cout <<k <<":" <<ENode[k].from <<" " <<ENode[k].to <<" " <<ENode[k].w <<endl;
        }
    }
    return 0;
}

 

 

邻接表

　　邻接表是图的一种链式存储结构。对于图中的每个顶点V_i ，把所有邻接于V_i 的顶点Vj 链成一个单链表，这个单链表称为顶点V_i 的邻接表。

　　邻接表有三种实现方式：动态建表实现，vector模拟链表实现和静态链表实现(链式前向星)；

动态建表

　　①储存结构(以无向图为例)

const int maxn= 1E+5;

struct ENode           //邻接表节点,边节点;
{
    int to;            //终点，边指向的点;
    int w;             //权;
    ENode * next;      //指向下一条边的指针;
};
struct VNode
{
    int from;          //起点表节点,点节点;
    ENode * first= NULL;     //表头指针，指向此点邻接表的第一个边节点;
};
VNode Adj[maxn];       //存储所有的点节点;

ENode是边类型，保存一条边的属性，是单链表的节点；next指针指向下一条边；

VNode是点类型，保存邻接表的表头，是单链表的起点；first指针指向单链表(V_i的邻接表)的第一个边节点。

　　②数据输入

    int n, m;
    cin >>n >>m;
    int a, b, w;
    //无向图建图;
    for (int i = 0; i < m; i ++)
    {
        cin >>a >>b >>w;
        ENode * p1= new ENode();
        p1->to= b;
        p1->w= w;
        p1->next= Adj[a].first;
        Adj[a].first= p1;
        ENode * p2= new ENode();
        p2->to= a;
        p2->w= w;
        p2->next= Adj[b].first;
        Adj[b].first= p2;
    }

同样，无向图要记得存两次边。

　　③遍历

    for (int i = 1;i <= n; i ++)
    {
        cout << i << ": ";
        for (ENode * k = Adj[i].first; k != NULL; k= k->next )
        {
            cout <<"-->" << k->to << " ";
        }
        cout << endl;
    }

以上面的例子测试程序：

可以看到，以1 出发，-->5 -->4 -->3 -->2; 这个顺序刚好与我们输入时的顺序相反，这是链式存储的特点；

　　对于无向图的邻接表，顶点V_i的入度恰好是第i个链表中的节点数；而在有向图中第i个链表的节点数只是V_i的出度。为了求入度，必须遍历整个邻接表或者建立一个逆邻接表(以V_i 为边终点的邻接表)。

　　对于动态建立的邻接表，他的时间效率是O(M)，空间效率也是O(M)。动态建表，不会浪费多余的空间，需要多少申请多少，但这些内存的释放就是个问题了(why?)。另外，一次申请内存和随机申请相比，再申请内存总量相同的情况下，前者明显消耗的时间更少，这也是邻接表的缺点之一。判断两个顶点V_i 和V_j 之间是否连接，需要搜索两条链表。

#include<iostream>
#include<algorithm>
#include<cstdio>
#include<cstring>
using namespace std;
const int maxn= 1E+5;

struct ENode           //邻接表节点,边节点;
{
    int to;            //终点，边指向的点;
    int w;             //权;
    ENode * next;      //指向下一条边的指针;
};
struct VNode
{
    int from;          //起点表节点,点节点;
    ENode * first= NULL;     //表头指针，指向此点邻接表的第一个边节点;
};
VNode Adj[maxn];       //存储所有的点节点;
int main()
{
    int n, m;
    cin >>n >>m;
    int a, b, w;
    //无向图建图;
    for (int i = 0; i < m; i ++)
    {
        cin >>a >>b >>w;
        ENode * p1= new ENode();
        p1->to= b;
        p1->w= w;
        p1->next= Adj[a].first;
        Adj[a].first= p1;
        ENode * p2= new ENode();
        p2->to= a;
        p2->w= w;
        p2->next= Adj[b].first;
        Adj[b].first= p2;
    }
    //遍历;
    for (int i = 1;i <= n; i ++)
    {
        cout << i << ": ";
        for (ENode * k = Adj[i].first; k != NULL; k= k->next )
        {
            cout <<"-->" << k->to << " ";
        }
        cout << endl;
    }
    return 0;
}

 

vector模拟链表

　　指用vector来模拟(代替)链表而实现邻接表。

　　①存储结构

const int maxn= 1E+5;

struct ENode           //邻接表节点,边节点;
{
    int to;            //终点，边指向的点;
    int w;             //权;
};
vector<ENode> Adj[maxn];

　　②数据输入

    int n, m;
    cin >>n >>m;
    int a, b, w;
    //无向图建图;
    for (int i = 0; i < m; i ++)
    {
        cin >>a >>b >>w;
        ENode e1, e2;
        e1.to= b;
        e1.w= w;
        Adj[a].push_back(e1);
        e2.to= a;
        e2.w= w;
        Adj[b].push_back(e2);
    }

　　③遍历

    for (int i = 1;i <= n; i ++)
    {
        cout << i << ": ";
        for (vector<ENode>::iterator it= Adj[i].begin(); it!= Adj[i].end(); it ++ )
        {
            ENode e= *it;
            cout <<"-->" <<e.to <<" ";
        }
        cout << endl;
    }

以上面的例子测试程序：

以1 出发，-->2 -->3 -->4 -->5; 这个顺序刚好与我们输入时的顺序相同，这是vector模拟与链式存储的不同；

和前一种实际的区别不大，可能优势是好写吧。

#include<iostream>
#include<algorithm>
#include<vector>
#include<cstdio>
#include<cstring>
using namespace std;
const int maxn= 1E+5;

struct ENode           //邻接表节点,边节点;
{
    int to;            //终点，边指向的点;
    int w;             //权;
};
vector<ENode> Adj[maxn];
int main()
{
    int n, m;
    cin >>n >>m;
    int a, b, w;
    //无向图建图;
    for (int i = 0; i < m; i ++)
    {
        cin >>a >>b >>w;
        ENode e1, e2;
        e1.to= b;
        e1.w= w;
        Adj[a].push_back(e1);
        e2.to= a;
        e2.w= w;
        Adj[b].push_back(e2);
    }
    //遍历;
    for (int i = 1;i <= n; i ++)
    {
        cout << i << ": ";
        for (vector<ENode>::iterator it= Adj[i].begin(); it!= Adj[i].end(); it ++ )
        {
            ENode e= *it;
            cout <<"-->" <<e.to <<" ";
        }
        cout << endl;
    }
    return 0;
}

 

静态链表(链式前向星)

　　邻接表的静态建表存储图的方式，也称链式前向星。链式前向星最开始是基于前向星，以提高其构造效率为目的设计的存储方式，最终形成的数据却是一个变形的邻接表。

　　链式前向星采用数组模拟链表的方式实现邻接表的功能，并且使用很少的额外空间，可以是说目前建图和遍历效率最高的存储方式。

　　①存储结构

const int maxn= 1E+5;

struct ENode           //邻接表节点,边节点;
{
    int to;            //终点，边指向的点;
    int w;             //权;
    int next;          //记录下一条边在ENode[]数组中的位置;
};
ENode Edegs[maxn];     //存放所有的边;
int Head[maxn];        //记录点Vi的第一条边在ENode中的位置;

ENode与之前在邻接表中的相似，都是保存边的属性，唯一不同的应该是"next指针"不再是指针类型，而是换成了int类型，储存的是下一条边在Edegs[ ]中的地址;

Head[ ]与在前向星中的功能相同，保存V_i 的第一条边在Edegs[ ]中的地址;

　　②数据输入

    int n, m;
    cin >>n >>m;
    int a, b, w;
    //无向图建图;
    memset(Head, -1, sizeof(Head));
    for (int i = 0; i < m* 2; i ++)
    {
        cin >>a >>b >>w;
        Edegs[i].to= b;
        Edegs[i].w= w;
        Edegs[i].next= Head[a];
        Head[a]= i;
        ++ i;          //无向图边存第二次;
        Edegs[i].to= a;
        Edegs[i].w= w;
        Edegs[i].next= Head[b];
        Head[b]= i;
    }

没什么特别的，记得每次更新Head[ ]即可；

　　③遍历

    //遍历;
    for (int i = 1;i <= n; i ++)
    {
        cout << i << ": ";
        for (int j= Head[i]; j!= -1; j= Edegs[j].next )
        {
            cout <<"-->" <<Edegs[j].to <<" ";
        }
        cout << endl;
    }

用上面的例子检验：

可以看出：

a. 以1 出发，-->5 -->4 -->3 -->2; 顺序与我们输入时的顺序相反，这是链式存储的特点，所以链式前向星对边的储存继承了邻接表(链式结构);

b.同样由上面看出，前向星原本对边排序的特性并没有保留下来(是否可以尝试继承呢？算了吧，少了排序省了好多时间呢 /笑)。

c.影响是？缺失了排序的原因是，使用链式的方式对同源的边进行连接，使之前对同一起点的边连续存放的必要性丢失，当然要找特定的边也更不好找了qaq。

#include<iostream>
#include<algorithm>
#include<vector>
#include<cstdio>
#include<cstring>
using namespace std;
const int maxn= 1E+5;

struct ENode           //邻接表节点,边节点;
{
    int to;            //终点，边指向的点;
    int w;             //权;
    int next;          //记录下一条边在ENode[]数组中的位置;
};
ENode Edegs[maxn];     //存放所有的边;
int Head[maxn];        //记录点Vi的第一条边在ENode中的位置;
int main()
{
    int n, m;
    cin >>n >>m;
    int a, b, w;
    //无向图建图;
    memset(Head, -1, sizeof(Head));
    for (int i = 0; i < m* 2; i ++)
    {
        cin >>a >>b >>w;
        Edegs[i].to= b;
        Edegs[i].w= w;
        Edegs[i].next= Head[a];
        Head[a]= i;
        ++ i;          //无向图边存第二次;
        Edegs[i].to= a;
        Edegs[i].w= w;
        Edegs[i].next= Head[b];
        Head[b]= i;
    }
    //遍历;
    for (int i = 1;i <= n; i ++)
    {
        cout << i << ": ";
        for (int j= Head[i]; j!= -1; j= Edegs[j].next )
        {
            cout <<"-->" <<Edegs[j].to <<" ";
        }
        cout << endl;
    }
    return 0;
}

 

谢谢各位看到最后。