【计算几何】二维凸包——Graham's Scan法

1 #include<algorithm> 2 #include<iostream> 3 #include<cstring> 4 #include<cstdio> 5 #include<cmath> 6 using namespace std; 7 const int maxn= 10010; 8 9 struct _point 10 { 11 double x, y; 12 _point (double _x= 0, double _y= 0) 13 { 14 x= _x; 15 y= _y; 16 } 17 /*friend: 修饰词:友元函数*/ 18 friend inline _point operator + (const _point &a, const _point &b) 19 { 20 return _point(a.x+ b.x, a.y+ b.y ); 21 } 22 friend inline _point operator - (const _point &a, const _point &b) 23 { 24 return _point(a.x- b.x, a.y- b.y ); 25 } 26 friend inline double operator * (const _point &a, const _point &b) 27 { 28 /*叉乘,求叉积*/ 29 /*x1y2- x2y1*/ 30 return (a.x* b.y)- (b.x* a.y); 31 } 32 }; 33 _point point[maxn]; 34 _point In_Bag[maxn]; 35 36 double getDis(_point a,_point b) 37 { 38 return sqrt((a.x-b.x)*(a.x-b.x)+(a.y-b.y)*(a.y-b.y)); 39 } 40 bool cmpx (const _point &a,const _point &b) 41 { 42 /*极角按逆时针排序(顺时针的点排在前面便是逆时针排序)*/ 43 /*叉积等于0,两向量平行*/ 44 double k= (a- point[0])* (b- point[0]); 45 return 0== k? (getDis(a, point[0])- getDis(b, point[0])<= 0): k< 0; 46 } 47 48 int cnt; //凸包集里点的个数; 49 void Graham_Scan(int n) 50 { 51 cnt= -1; 52 In_Bag[++ cnt]= point[0]; 53 for(int i= 1; i< n; i ++) 54 { 55 while(cnt&& (point[i]- In_Bag[cnt])* (In_Bag[cnt]-In_Bag[cnt- 1])< 0 ) 56 { 57 /*当In_Bag中至少有基点和另一点时(cnt>= 1)*/ 58 /*逆时针扫描时,如果向量{pn- 1, pn}与{pn, pn+ 1}的叉积为负,则将上一点删除*/ 59 /*顺时针扫描判断是否为正*/ 60 -- cnt; 61 } 62 In_Bag[++ cnt]= point[i]; 63 } 64 } 65 66 int main() 67 { 68 int n; 69 double xx, yy; 70 while (~ scanf("%d", &n)) 71 { 72 for (int i= 0; i< n; i ++) 73 { 74 scanf("%lf %lf", &xx, &yy); 75 if (i) 76 { 77 if (yy< point[0].y|| (yy== point[0].y&& xx< point[0].x)) 78 { 79 double tmp= yy; 80 yy= point[0].y; 81 point[0].y= tmp; 82 tmp= xx; 83 xx= point[0].x; 84 point[0].x= tmp; 85 } 86 } 87 point[i].x= xx; 88 point[i].y= yy; 89 } 90 sort(point+ 1, point+ n, cmpx); 91 Graham_Scan(n); 92 93 /*求凸包周长*/ 94 double Dis= 0; 95 // cout << "********************" << endl; 96 // for (int i= 0; i<= cnt; i ++) 97 // { 98 // cout << In_Bag[i].x << " " << In_Bag[i].y << endl; 99 // } 100 for (int i= 0; i<= cnt; i ++) 101 { 102 Dis+= getDis(In_Bag[i], In_Bag[(i+ 1)% (cnt+ 1)]); 103 } 104 printf("%.2f\n", Dis); 105 } 106 return 0; 107 }
凸包
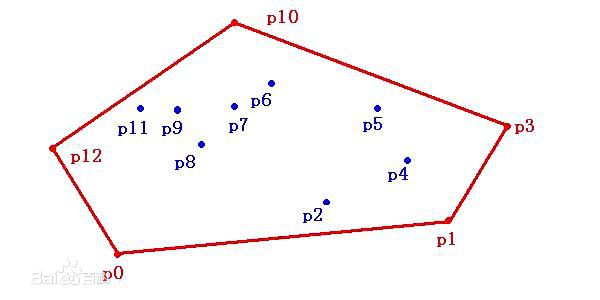
点集Q的凸包(convex hull)是指一个最小凸多边形,满足Q中的点或者在多边形边上或者在其内。右图中由红色线段表示的多边形就是点集Q={p0,p1,...p12}的凸包。
一组平面上的点,求一个包含所有点的最小的凸多边形,这就是凸包问题了。这可以形象地想成这样:在地上放置一些不可移动的木桩,用一根绳子把他们尽量紧地圈起来,并且为凸边形,这就是凸包了。
数学定义:设S为欧几里得空间Rn的任意子集。包含S的最小凸集称为S的凸包,记作conv(S)。
【百度百科】https://baike.baidu.com/item/%E5%87%B8%E5%8C%85/179150?fr=aladdin
以下内容基本照搬。
凸包最常用的凸包算法是Graham扫描法和Jarvis步进法
①Graham's Scan法
这个算法是由数学大师葛立恒(Graham)发明的。
⒈ 在所有点中选取y坐标最小的一点H,当作基点。如果存在多个点的y坐标都为最小值,则选取x坐标最小的一点。坐标相同的点应排除。
2.然后按照其它各点p和基点构成的向量<H,p>;与x轴的夹角进行排序,夹角由大至小进行顺时针扫描,反之则进行逆时针扫描。实现中无需求得夹角,只需根据余弦定理求出向量夹角的余弦值即可。
以下图为例,基点为H,根据夹角由小至大排序后依次为H,K,C,D,L,F,G,E,I,B,A,J。下面进行逆时针扫描。
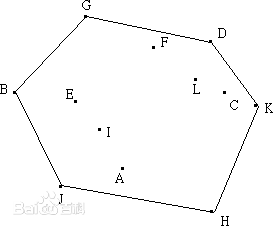
3.线段<H,K>;一定在凸包上,接着加入C。假设线段<K,C>;也在凸包上,因为就H,K,C三点而言,它们的凸包就是由此三点所组成。但是接下来加入D时会发现,线段<K,D>;才会在凸包上,所以将线段<K,C>;排除,C点不可能是凸包。即当加入一点时,必须考虑到前面的线段是否在凸包上。从基点开始,凸包上每条相临的线段的旋转方向应该一致,并与扫描的方向相反。如果发现新加的点使得新线段与上线段的旋转方向发生变化,则可判定上一点必然不在凸包上。实现时可用向量叉积进行判断,设新加入的点为Pn+1,上一点为Pn,再上一点为Pn-1 。顺时针扫描时,如果向量{Pn-1 ,Pn}与{Pn,Pn+1}的叉积为正(逆时针扫描判断是否为负),则将上一点删除。删除过程需要回溯,将之前所有叉积符号相反的点都删除,然后将新点加入凸包。
4.在上图中,加入K点时,由于线段<H,C>要旋转到<H,K>的角度,为顺时针旋转,所以C点不在凸包上,应该删除,保留K点。接着加入D点,由于线段<K,D>要旋转到<H,K>的角度,为逆时针旋转,故D点保留。按照上述步骤进行扫描,直到点集中所有的点都遍历完成,即得到凸包。
向量的叉积
向量积,数学中又称外积、叉积,物理中称矢积、叉乘,是一种在向量空间中向量的二元运算。与点积不同,它的运算结果是一个向量而不是一个标量。并且两个向量的叉积与这两个向量和垂直。
两个向量a和b的叉积写作a×b(有时也被写成a∧b,避免和字母x混淆)。
向量积|c|= |a×b|= |a||b|sin<a,b>;c的方向遵守右手定则。c是垂直a、b所在平面,且以|b|·sinθ为高、|a|为底的平行四边形的面积。
c = a×b=(x1y2- x2y1);
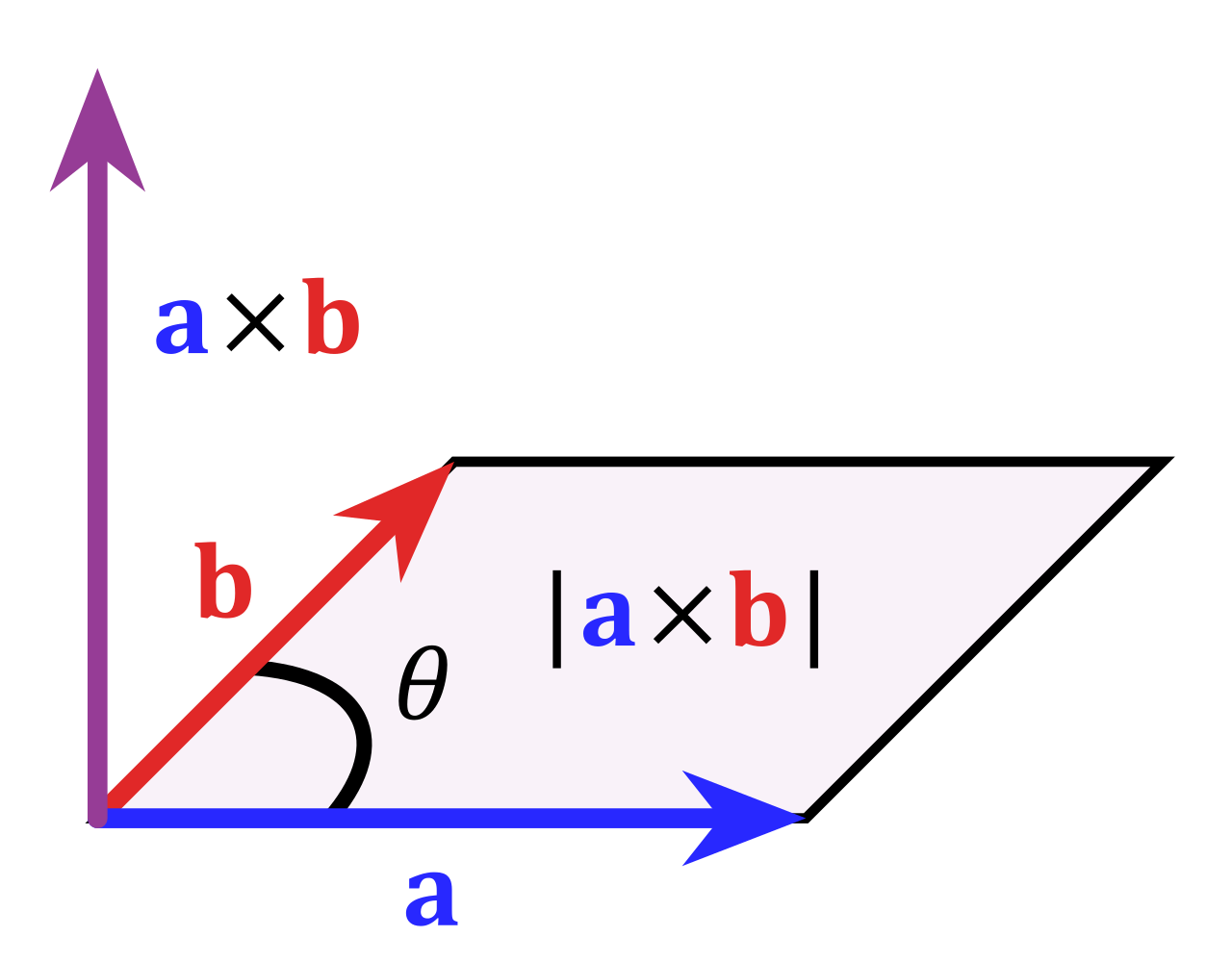
【图源维基百科】
维基百科中向量积解释:https://en.wikipedia.org/wiki/Cross_product
下面放一个例子吧;
【洛谷】P2742 【模板】二维凸包 / [USACO5.1]圈奶牛Fencing the Cows
题目描述
农夫约翰想要建造一个围栏用来围住他的奶牛,可是他资金匮乏。他建造的围栏必须包括他的奶牛喜欢吃草的所有地点。对于给出的这些地点的坐标,计算最短的能够围住这些点的围栏的长度。
输入格式:
输入数据的第一行包括一个整数 N。N(0 <= N <= 10,000)表示农夫约翰想要围住的放牧点的数目。接下来 N 行,每行由两个实数组成,Xi 和 Yi,对应平面上的放牧点坐标(-1,000,000 <= Xi,Yi <= 1,000,000)。数字用小数表示。
输出格式:
输出必须包括一个实数,表示必须的围栏的长度。答案保留两位小数。
这是一道二维凸包模板题。我按上面的步骤一点点拆分一下。
首先两个pair数组,分别存放所有的点和位于凸包上的点。
const int maxn = 10005; typedef pair<double, double> _pair; _pair point[maxn]; _pair In_Bag[maxn];
之所以用pair是因为二维坐标刚好两个点,有便宜不占嘿嘿嘿。
然后一些基本的计算几何公式;
计算两点间距离。
double Get_Dis (_pair point1, _pair point2) { //计算两点间距离 return sqrt(((point1.first- point2.first)* (point1.first- point2.first) ) + ((point1.second- point2.second)* (point1.second- point2.second) ) ); }
计算叉积。
double Get_axb (_pair a_point1, _pair a_point2, _pair b_point1, _pair b_point2) { //计算两条向量的叉积 //向量a= a_point1 --> a_point2= a_point2- a_point1; //向量b= b_point1 --> b_point2= b_point2- b_point1; //叉积axb= (a.x* b.y)- (b.x* a.y); //a.x= a_point2.x- a_point1.x; a.y= a_point2.y- a_point1.y; return (((a_point2.first- a_point1.first)* (b_point2.second- b_point1.second) ) - ((b_point2.first- b_point1.first)* (a_point2.second- a_point1.second) ) ); }
计算向量a和x轴所成角的余弦值。
double Get_Cos (_pair point1, _pair point2) { //计算向量a(point1-->point2) 的余弦值; point2.first-= point1.first; //把point1看作坐标原点(0, 0); point2.second-= point1.second; //则point2的坐标为(P2.x- P1.x, P2.y- P1.y); point1.first= 0; point1.second= 0; _pair point3; //在X轴上找一点P3,做直角三角形; point3.first= point2.first; //P3.x= P2.x; point3.second= 0; //P3.y= P1.y= 0; double Dis_P1_P2= Get_Dis(point1, point2); //计算直角三角形的斜边长,即P1P2之间的距离; return point3.first/ Dis_P1_P2; //邻边/ 斜边; }
确定了基点后,围绕基点对其余点排序(按余弦值),判断函数cmp。
bool cmpx_1 (_pair a, _pair b) { //小于运算(按与基点P0所成向量的余弦值大小,余弦值越大越优先;cosx在[0,Pi]内从1到-1,减函数; //排序后,按逆时针方向遍历点集; _pair tmp = point[0]; //基点; double Cos_a = Get_Cos(tmp, a); //求出a,b的余弦值; double Cos_b = Get_Cos(tmp, b); return Cos_a- Cos_b> 0; //余弦值越大越优先(越大逆时针遍历越靠前); }
主函数中,在输入时先确定基点point[0],然后对其余点按逆时针顺序排序。
for (int i = 0; i < n; i ++) { cin >> x >> y; if (i ) { if (y< point[0].second|| (y== point[0].second&& x< point[0].first) ) { double tmp= y; y= point[0].second; point[0].second= tmp; tmp= x; x= point[0].first; point[0].first= tmp; } } point[i].first= x; point[i].second= y; } sort(point+ 1, point+ n, cmpx_1);
对排序后的点集,判断是否加入In_Bag[]。
int cnt= -1; //cnt -->In_Bag[]中最后一位元素的数组下标; In_Bag[++ cnt]= point[0]; for (int i = 1; i < n; i ++) //从point[1]开始; { while (cnt&& Get_axb(In_Bag[cnt- 1], In_Bag[cnt], In_Bag[cnt], point[i])< 0 ) { //当In_Bag中至少有基点和另一点时(cnt>= 1时); //逆时针扫描时,如果向量{Pn-1, Pn}与{Pn, Pn+1}的叉积为负,则将上一点删除; //(顺时针扫描判断是否为正) -- cnt; } In_Bag[++ cnt]= point[i]; }
最后把所有点首尾相连,算出距离和即可。
double Dis = 0; for (int i= 0; i<= cnt; i ++) { Dis+= Get_Dis(In_Bag[i], In_Bag[(i+ 1)% (cnt+ 1)]); } printf("%.2f\n", Dis);
谢谢各位能看到最后嘿嘿。
完整的代码在这里。




