集成学习多样性的数学分析 —— 误差分歧分解

 

1、集成学习背景

假定我们用个体学习器h₁, h₂, ..., h_T通过加权平均法结合产生集成来完成回归学习任务f：R^d => R：

                                                      

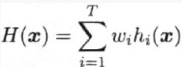
2、分歧（ambiguiry）

个体学习器h_i的分歧

对示例x，定义学习器h_i的分歧为：

　　                        

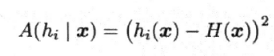
集成的分歧

对示例x，定义集成的分歧为：

                         

 

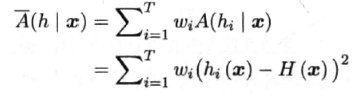
集成分歧表征了个体学习器在样本x上的不一致性，即在一定程度上反映了个体学习器的多样性。

3、个体学习器h_i和集成H的平方误差

个体学习器hi的平方误差：

                       

 

 

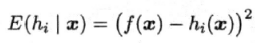
 个体学习器误的加权平均值 ：

                        

 

 

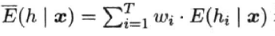
 集成H的平方误差：

　　　　　      

---

 

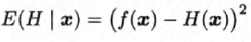
4、误差-分歧分解（error-ambiguity decomposition）

step 1

将平方误差带入集成分歧中得：

                            

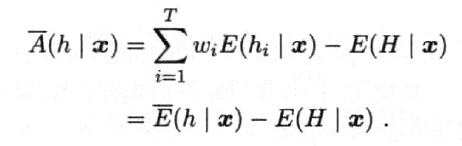
该式对所有样本x均成立。

step 2

令 p(x) 表示样本的概率密度，则在全样本上有（对step 1式两边对x积分）：

            

 

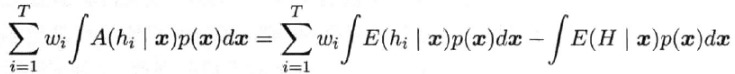
step 3

个体学习器h_i在全样本上的泛化误差：

              

个体学习器h_i泛化误差的加权均值：

             

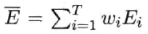
个体学习器h_i在全样本上的分歧项：

               

个体学习器h_i的加权分歧值：

               

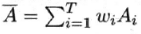
 集成的泛化误差：

               

 

step 4

集成的泛化误差E（误差-分歧分解）：

　　     

 

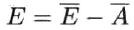
这个式子指出：

　　个体学习器准确性越高、多样性越大，则集成越好。

 

上面这个分析首先由[Krogh and Vedelsby, 1995]给出，称为误差-分歧分解。

Remark

　　看到这，大家可能回想：如果直接把 作为优化目标来求解，不就能得到最优的集成了？

　　遗憾的是，现实任务中很难直接对该式进行优化，不仅由于它们是定义在整个样本空间上，还由于不是一个可直接操作的多样性度量，它仅在集成构造好之后才能进行估计。

 

　　需要注意的是，上面的推导过程只适用于回归学习，难以直接推广到分类学习任务上去。