模式识别 —— 线性判别函数决策面的数学知识

以下问题均是基于二分类：

1、线性判别函数

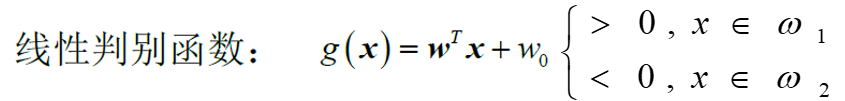
    若 g(x) = 0，则x落在分类面H上。

 

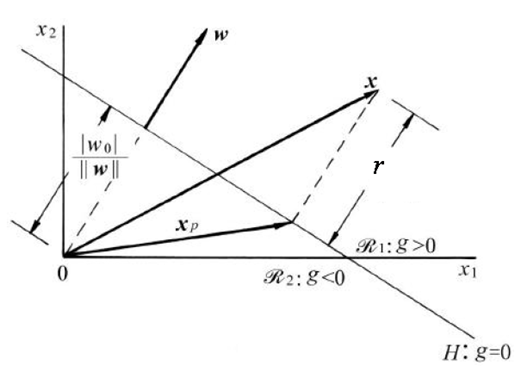
2、w 是 决策面g(x) = 0 的法向量

假设 x₁ 和 x₂ 都落在决策面H上，则 g(x₁) = g(x₂) = 0

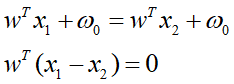
这说明：w和超平面H上任一向量正交，即w时H的法向量。

 

当x在R₁中时，g(x) > 0，决策面的法向量指向R₁，R₁中的所有x在H的正侧；

当x在R₂中时，g(x) < 0，决策面的法向量的反方向指向R₂，R₂中的所有x在H的负侧。

 

3、样本x与超平面H的距离r

 

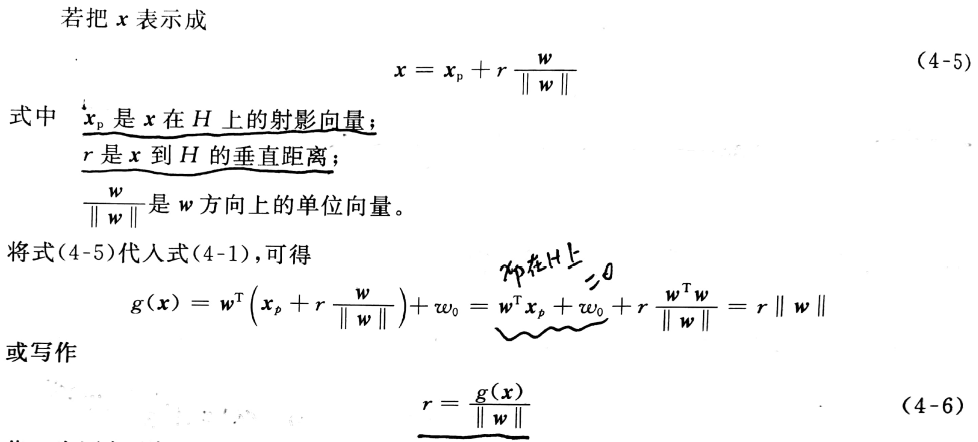
4、原点x₀与超平面H的距离r₀

 图4-1即标题序号2中的大图。

 

5、超平面H的方向和位置的决定因素

利用线性判别函数进行决策，就是用一个超平面把特征空间分割成两个决策区域。

超平面的方向：权向量w

超平面的位置：阈值权w₀