编译原理（四）语法分析之自顶向下分析

语法分析之自顶向下分析

说明：以老师PPT为标准，借鉴部分教材内容，AlvinZH学习笔记。

基本过程分析

1. 一般方法：对任一字符串，试图用一切可能的方法，从树根节点（开始符号）出发，根据文法自上而下地为输入符号串建立一棵语法树。直观理解为从开始符号出发，依据规则建立推导序列，最后推至目标字符串。

2. 特点：分析过程是带有预测的，是一种试探过程。试探失败就会出现回溯问题，降低了分析的效率。

3. 存在问题：左递归问题、回溯问题。

问题一：左递归问题

1. 左递归文法：文法规则中有形如 \(U::=U···\) 或 $ U=+>U···$。

为什么自顶向下分析不能处理左递归？
答：试想，若遇到非终结符U时，尝试用该规则右部 "U···" 去匹配字符串，下一步又要匹配U，又要尝试用用该规则右部 "U···" 右部去匹配，无限循环无终止。

2. 消除左递归

（1）直接消除左递归：令扩充的BNF表示法改写文法规则。例如对于规则 \(E∷= E + T | T\)，改写为 \(E∷= T { + T }\)。（提醒一下，这里是正则文法表达，不是正则表达式，重复别写成了(+T)*）。

如何改写？方法如下：

• 规则一：提（前缀）公因子。对于 \(U∷= x y | x w |….| x z\)，改写为U∷= x ( y | w |….| z )。
• 规则二：对于 \(U∷= x | y |…| z | U v\)，改写为 $ ( x | y |…| z ) { v }$。具有一个直接左递归的右部，可直接改写为重复。

注意：

①对于规则 \(U::=x|xy\)， 应该改写成 \(U ::= x (y | ε)\)，而不是 \(U ::= x (ε | y)\)，因为这个神奇的 \(ε\) 总是作为最后的选择，约定其可以与任何字符相匹配（还没懂？如果放前面，那它可以和U匹配，岂不还是左递归？）。

②作用：不仅有助于消除直接左递归，而且有助于压缩文法的长度，使我们更加有效地分析句子。

通过以上两条规则，就能消除文法的直接左递归，并且保证文法的等价性。

（2）将左递归改写成右递归

• 规则三：对于 \(P∷= P α | β\)，可改写为 \(P ::= βP' , P' ::= αP' | ε\)。

（3）教材中提及一个算法，可以消除一般的左递归（不存在产生式形如 \(A::=A\) 或 \(A::= ε\)），看伪代码理解起来还真有点难，不过理解一下跟着的拿到例题，其实不过是对于不存在直接左递归的产生式直接代入其他产生式化简罢了，有一点点像把正则文法转换成正则表达式的感觉（依然得记得扩展BNF与正则式的区别）。

【例题】消除规则 \(E∷= E + T | T\) 的左递归。

解：方法一：利用规则二，直接改写成 \(E ::= T {+T}\)。

方法二：利用规则三，改为右递归，\(E ::=ET' , E' ::= +TE' | ε\)。

问题二：回溯问题

1. 原因：某个非终结符号的规则其右部有多个选择，并根据所面临的输入符号不能准确地确定所要的产生式，就可能出现回溯。回溯的后果是效率极低且代价极高，具体一点就是写不出代码。效率低的原因是语法分析要重做，精确定位，尝试的语法处理工作需要推倒重来。

2. 如何避免回溯？大家注意了，第一个重要的集合就要出现了，它就是——FIRST()集合！

FIRST集合定义：在不具有左递归的文法G中，U∈Vn，有规则形如 U::= α1 | α2 | ... | αn，则有 FIRST(αi) = {a | αi =*> a... , a∈Vt}。

如何理解这个FIRST集合呢？中文名叫做首字符集，意思是如果选择从 \(α_i\) 出发，最后可以推到很多终结符号串（个人认为写成句子好理解一些），取得这些符号串的第一个字符组成FIRST集。对于之后LL分析法中非终结符的FIRST集合也是这样理解的，不过在这里我们求得是每个右部选择的FIRST集。

3. 好了，问题来了那怎么用上这个FIRST集呢？结合定义以及回溯出现的原因，为何避免回溯，必须保证每一步的选择是对的（如果之后匹配不上，可直接判定不是文法的句子二不需要犹豫是不是当初选择错了），因此文法需保证：

对于文法中的任意一个非终结符，若其规则右部存在多个选择，各个选择推出的终结符号串的头符号集两两不相交。（必要条件）

4. 新的问题，万一文法不符合上述条件，我非要用自顶向下怎么办？不是不可以，两种方法如下：

（1）对文法再次进行改写加工。注意文法的先行条件：不具有左递归。在此基础上，只需要对不满足条件的产生式的多个规则右部反复提取左因子，最后总是可以做到符合上述条件的。

举个栗子，\(U ::= xV | xW\)，明显FIRST(xV)与FIRST(xW)相交，改写成 \(U ::= x(V |W)\)就可以了（当然非终结符 V 和 W 也要重点关注一下）。

（2）超前扫描：对于不满足上述条件的文法，采用超前扫描的方法，即向前侦察各输入符号串的第二个、第三个符号来确定要选择的目标。

本质上来讲也有回溯的味道，因此比第一种方法费时，但是读的仅仅是向前侦察情况，不作任何语义处理工作。

问题总结

在不采取超前扫描的前提下实现不带回溯的自顶向下分析，对文法需要满足两个条件：

• 文法是非左递归的；
• 对文法的任一非终结符，若其规则右部有多个选择时，各选择所推出的终结符号串的首符号集合要两两不相交。

注意：书中也提到了满足这两个条件有可能构造，意味着上述两个条件是必要条件，不是充要条件。为什么？个人认为在LL分析法中再次提到了这个问题，与另一个重要的集合 FOLLOW集 有关，但是在那里说的是判断LL(1)文法的充要条件，不知道有没有什么区别。

递归子程序法（递归下降分析法）

1. 方法：对文法的每一个非终结符都编一个分析子程序，完成对该非终结符语法成分的分析与识别任务。当根据文法和当时的输入符号预测到要用某个非终结符去匹配输入串时，就调用该非终结符的分析程序。

为何名为递归下降？由于这是自顶向下分析方法，且子程序的调用过程中允许（直接或间接的）递归调用。

2. 要求：消除左递归。允许存在右递归和自嵌入式递归。

3. 递归子程序法对应的是最左推导过程。方法比较简单，UI大作业中也要求用到了，这里不再多说了。

LL（1）分析法

1. 为何名为LL（1）？

• LL：自左向右扫描、自左向右地分析和匹配输入串。分析过程表现为最左推导的性质。
• （1）：分析过程中，美进行一步推导，只要向前查看一个输入符号，便能确定当前应选择的产生式。

2. LL分析程序构造及分析过程

（1）LL（1）分析器组成：分析表、执行程序 (总控程序）、符号栈 （分析栈）。

• 分析表是一个二维矩阵M，M[A,a] = A::=αi 或者 error，表示非终结符A遇到当前字符为a时，应该使用哪一个右部去匹配，或者出错。
• 符号栈：开始状态、工作状态、出错状态、结束状态。
• 执行程序：算法暂不描述。

注意： 对于M[A,a] = A::=αi，此时应该将A退出符号栈，并将 αi 逆序压入栈中（为了符合最左推导的要求）。

（2）举个例子，算了，直接说如何构造分析表吧！

3. LL（1）分析表的构造

（1）\(α\) 的头符号集 FIRST(α)。假定 \(α\) 是文法G的任意符号串，即 \(α∈V^*\)，则有 \(FIRST(α) = {a | α =*> a···, a∈V_t}\)。特别的，若有 \(α =*> ε\)，则规定 \(ε ∈ FIRST(α)\)。

如何理解FIRST(α)？简单来说，FIRST(α)就是由 \(α\) 可能推导出的所有符号串的第一个终结符号或可能的 \(ε\) 组成的集合。

（2）\(A\) 的后继符号集 FOLLOW(A)。对于文法G的任何非终结符A，开始符号为S，定义：\(FOLLOW(A) = {a | S =*> ···Aa···, a∈V_t}\)。特别的，若 \(S =*> ···A\)，则 #∈FOLLOW(S)。

如何理解FOLLOW(A)？单词英文意思就是跟随，简单来说，FOLLOW(A)是所有句型中紧跟在A之后的非终结符或#组成的集合。

（3）构造FIRST集合

算法说明：对于文法G中的每一个字符X∈V，计算FIRST(X)，反复应用如下规则，直至FIRST集不再增大。

• 若 \(X∈V_t\)，则 \(FIRST(X) = {X}\) 。
• 若 \(X∈V_n\)，且存在 \(X→aα\) 产生式（a∈Vt），则 \(a∈FIRST(X)\)。若有 \(X→ε\)，则 \(ε ∈ FIRST(X)\)。
• 若存在 \(X→Y1Y2...Yk\) 产生式，若 \(Y1∈V_n\)，则FIRST(Y1)中所有非 \(ε\) 符号加进FIRST(X)。对于一切 \(2≤ i ≤k\)，若 \(Y1\)、\(Y_2\)、...、\(Y_{i-1}\) 均为非终结符，且 \(ε ∈ FIRST(Y_{1~i-1})\)，则FIRST(Yi)中的非 \(ε\) 符号加进FIRST(X)。特别地，若对于所有 \(Y_{1~k}\)，都有 \(ε ∈ Y_{1~k}\)，则 $ε ∈ FIRST(X)。

理解与应用：

• 一般来说，求解FIRST集合是从最后一个产生式开始往上推。当然，最后还得正序检查一遍，防止递归造成不完整。
• 算法第三点看起来很长，其实很好理解，记住FIRST(X)集合的定义——头符号集，尽可能找到所有可能出现在X推出符号串的非终结符或 \(ε\) 集合。

（4）构造FOLLOW集合

算法说明：对于文法G中每一个非终结符A，计算FOLLOW(A)，反复应用如下规则，直至FOLLOw集不再增大。

• 若A为开始符号S，则#∈FOLLOW(A)。
• 若 \(A ::= αBβ\)，且\(β ≠ ε\)，则将FIRST(β)中一切非 \(ε\) 符号加进FOLLOW(A)。
• 若 \(A ::= αBβ\)，若有 \(ε ∈ FIRST(β)\)，则FOLLOW(A)中一切符号加进FOLLOW(B)。

理解与应用：

• 注意到 \(ε\) 是不会出现在FOLLOW集合中的。
• 还是一句话，记住定义。FOLLOW(A)表示A的后继符号集，意思是A后面可能会出现的所有终结符或#集合。

（5）构建LL（1）分析表

在求出了每一个产生式的个候选式的FIRST集以及每一个非终结符的FOLLOW集之后，文法G的LL（1）分析表构造算法如下：对于文法G的每一个产生式A→α

• 对FIRST(α)中的每个终结符a，置 \(M[A,a] = A→α\)。
• 若 \(ε ∈ FIRST(α)\)，则对FOLLOW(A)中的每一个符号b，置 \(M[A,b] = A→ε\)。
• M中所有不满足上述两条的位置置为空，即error。

（6）实例分析

例：已知文法G[E]：①\(E∷= T E’\)；②\(E’∷= + T E’ | ε\)；③\(T∷= F T’\)；④\(T’∷= * F T’ | ε\)；⑤\(F∷= ( E ) | i\)。构造LL（1）分析表。

解：（1）求FIRST集：（从下往上）

FIRST((E)) = { ( } ，FIRST( i ) = { i }；
FIRST(*FT’) = { * }，FIRST( ε ) = { ε }；
FIRST(FT’) = { ( , i }；
FIRST(+TE’) = { + };
FIRST(TE’) = { ( , i };

（2）求FOLLOW集：（从上往下）

FOLLOW(E) = { # , ) }；
FOLLOW(E’) = { # , ) }；
FOLLOW(T) = { + , ) , # }；
FOLLOW(T’) = FOLLOW(T) = { + , ) , # }；
FOLLOW(F) = { * , + , ) , # }；

（3）构造分析表

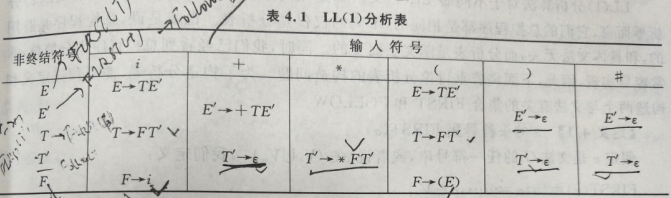
（4）分析句子

（只分析了一半，看懂了就行）

4. LL（1）文法

（1）若文法G构造出的LL（1）分析表M不含有多重定义元素，称之为LL（1）文法。LL（1）文法是无二义的。由某LL（1）文法产生的语言称为LL（1）语言。

可以证明，如果G是左递归或二义的，那么M至少含有一个多重定义入口。

（2）充要条件：一个文法G是LL（1）文法，当且仅当对于G的每一个非终结符A的任意两条不同规则 \(A ::= α | β\)，下了条件成立：

• FIRST(α) ∩ FIRST(β) = Ф；
• 若 \(β =*> ε\)，则FIRST(α) ∩ FOLLOW(A) = Ф。

（3）重要结论

• 任何LL（1）文法都是无二义性的。
• 若文法中含有左递归规则，则必然是非LL（1）文法。
• 存在一种算法，它能判断一个文法是否是LL（1）文法。（利用充要条件）
• 存在一种算法，它能判定两个LL（1）文法是否产生相同语言（即等价）。（比较LL(1)分析表）
• 不存在算法，它能判定任意的上下文无关语言是否由LL（1）文法产生。
• 非LL（1）语言是存在的。
• 有些文法可以从非LL(1)文法改写为LL(1)文法，但并不是所有的非LL(1)文法都能改写为LL(1)文法。

证明一下？同学你这是要我的命，快去看看自底向上分析吧！

引用说明

- 邵老师课堂PDF
- 《编译原理级编译程序构造》