AGC008_E Next or Nextnext

图片搬运来源
https://blog.csdn.net/litble/article/details/83118814

题面翻译
题面给定一个长度为N的序列p，问有多少种长度为N的排列q，符合以下条件：对于每个1<=i<=N,满足\(q_i=p_i || q_{q_i}=p_i\)。

思路
我们先定义一张有向图，它是由一个序列a构造出来的，其中图中的每条边\(u->v\)，都满足\(a_u=v\)，简单来说，就是对于这个序列，\(i\)向\(a_i\)连边。
然后我们再反过来考虑题目。我们现在手上有一个排列q，它会符合哪些序列呢？
显然对于一个排列构造出来的图一定是多个环。我们先举个例子，画出其中的一个环。

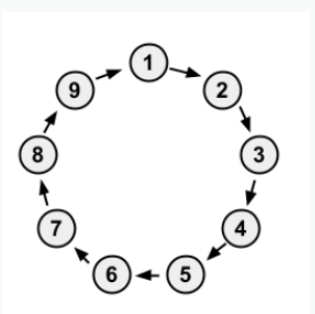
那么对于原序列p，有四种情况：

1.所有的\(p_i\)均为\(i\)所指的点（即均满足\(q_i=p_i\))，环不变。

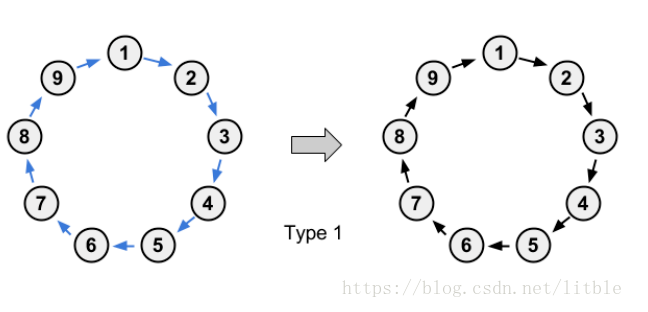
2.所有的\(p_i\)均为\(q_i\)所指的点（即均满足\(q_{q_i}=p_i\)），且环的大小为奇数，环的大小不变，每个点的指向有所改变。

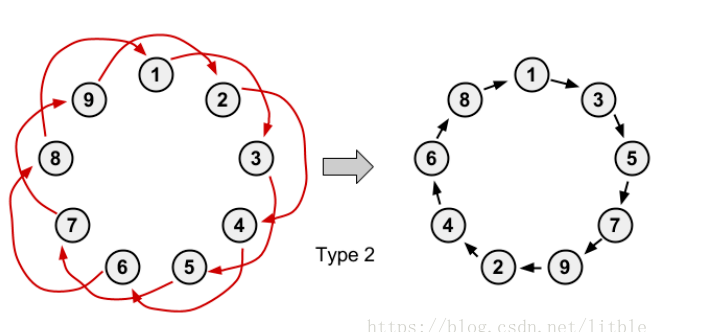
3.所有的\(p_i\)均为\(q_i\)所指的点（即均满足\(q_{q_i}=p_i\)），且环的大小为偶数，分裂成两个大小相同的环。

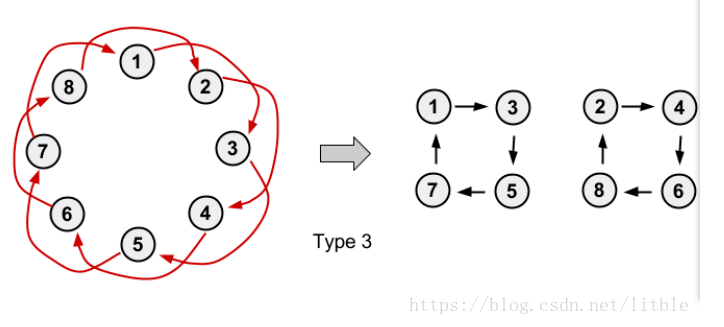
4.部分\(p_i\)满足为\(i\)所指，部分\(p_i\)满足为\(q_i\)所指，演变成一个由一个环和多个链组成的基环内向树。

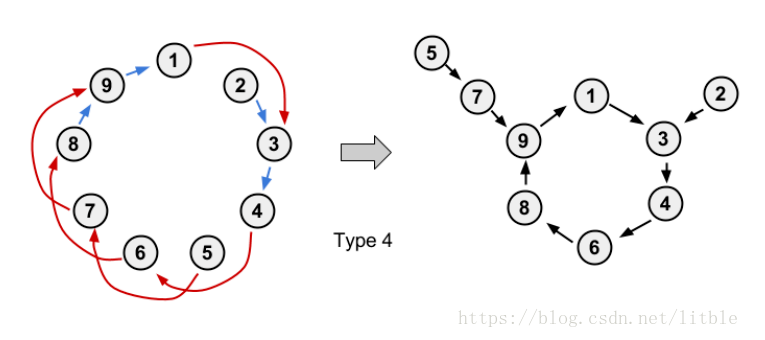
但是现在我们只知道\(p_i\)构成的图，如何推出\(q_i\)？
对于环，把长度相同的放在一起做个dp，转移直接枚举他们的变化情况。
对于一棵基环内向树，我们考虑每个挂在环上的链，如何把它们塞到环里面去，而且相邻两个点中间最多间隔一个点?大致如下图：

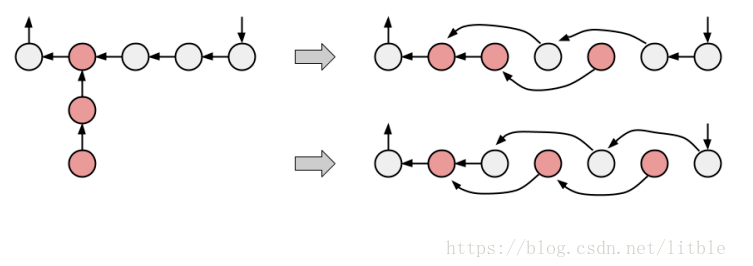
我们设这条链到下一条链之间有\(l_2\)条边，这条链有\(l_1\)条边，那么塞进链的方案数为：

\[\begin{cases}0&l_1>l_2\\ 1&,l_1=l_2\\ 2&,l_1<l_2\end{cases} \]

然后我们乘一乘即可算出答案。

#include<cmath>
#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
using namespace std;
const int maxn=1e5;
const int mod=1e9+7;
int n,cnt,ans=1;
int a[maxn+8],deg[maxn+8],vis[maxn+8],cir[maxn+8],l1[maxn+8],l2[maxn+8],sum[maxn+8];
int f[maxn+8];
bool tree[maxn+8];

int read()
{
    int x=0,f=1;char ch=getchar();
    for (;ch<'0'||ch>'9';ch=getchar()) if (ch=='-') f=-1;
    for (;ch>='0'&&ch<='9';ch=getchar()) x=x*10+ch-'0';
    return x*f;
}

void solve(int x)
{
    int siz_line=0;
    while(!cir[x]) siz_line++,x=a[x];
    l1[x]=siz_line;
    tree[cir[x]]=1;
    siz_line=1,x=a[x];
    while(deg[x]!=2) siz_line++,x=a[x];
    l2[x]=siz_line;
}

int main()
{
    n=read();
    for (int i=1;i<=n;i++) a[i]=read(),deg[a[i]]++;
    for (int i=1;i<=n;i++)
	{
	    if (vis[i]) continue;
	    int x=i;
	    while(!vis[x]) vis[x]=i,x=a[x];
	    if (vis[x]!=i) continue;
	    ++cnt;
	    while(!cir[x]) cir[x]=cnt,x=a[x];
	}
    memset(vis,0,sizeof(vis));
    for (int i=1;i<=n;i++) if (deg[i]>(1+(cir[i]>0))) {puts("0");return 0;}
    for (int i=1;i<=n;i++) if (!deg[i]) solve(i);
    for (int i=1;i<=n;i++)
	if (l1[i]) ans=1ll*ans*((l2[i]>=l1[i])+(l2[i]>l1[i]))%mod;
    for (int i=1;i<=n;i++)
	{
	    if (!cir[i]) continue;
	    if (tree[cir[i]]) continue;
	    if (vis[i]) continue;
	    int x=i,siz=0;while(!vis[x]) siz++,vis[x]=1,x=a[x];
	    sum[siz]++;
	}
    for (int i=1;i<=n;i++)
	{
	    if (!sum[i]) continue;
	    //printf("%d %d\n",i,sum[i]);
	    f[0]=1;
	    for (int j=1;j<=sum[i];j++)
		{
		    f[j]=f[j-1];
		    if (i>1&&(i&1)) f[j]=(f[j]+f[j-1])%mod;
		    if (j>1) f[j]=(f[j]+1ll*f[j-2]*(j-1)%mod*i%mod)%mod;
		}
	    ans=1ll*ans*f[sum[i]]%mod;
	}
    printf("%d\n",ans);
    return 0;
}