AGC006_B Median Pyramid Easy
图片搬运来源:官方
题面翻译
有一个n层的金字塔,从上往下数第i层有2*i-1个格子,呈中心对齐状。对于金字塔上的每个格子填的数(不包括第n层上的),它等于下面一层的对应位置上和向左一格的位置上,以及向右一格的位置上的三个数的中位数。那么当我们确定第n层上的数时,整个金字塔每个位置上的数也就确定了。如下图:
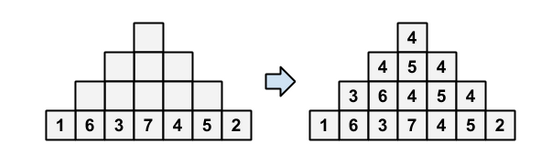
给定第一层的格子上的数,构造一种第n层的填数方案满足此
条件。
思路
手玩好题呀。
对于金字塔的某一层,如果存在某两个相邻的格子上填了相同的数,那么这两个格子向上所有对应的位置上都会是这个数,如下图:
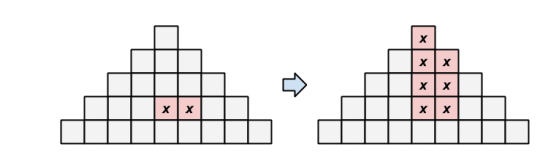
那么就很好构造了。我们只要满足第n-1层中心线与其向右一格的位置上均为给定的数,其余的位置随便填就行。至于具体细节可以自己思考一下,或者详见代码。
#include<cmath>
#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
using namespace std;
const int maxn=1e5;
int n,x;
int a[maxn*2+8];
int read()
{
int x=0,f=1;char ch=getchar();
for (;ch<'0'||ch>'9';ch=getchar()) if (ch=='-') f=-1;
for (;ch>='0'&&ch<='9';ch=getchar()) x=x*10+ch-'0';
return x*f;
}
int main()
{
n=read(),x=read();
if (x==1||x==2*n-1)
{
puts("No");
return 0;
}
if (n==2)
{
puts("Yes");
puts("1 2 3");
return 0;
}
a[n]=x;
if (x==2)
{
a[n-1]=x+1,a[n+1]=x-1,a[n+2]=x+2;
int now=1;
for (int i=1;i<n-1;i++)
{
if (now==x-1) now=x+3;
a[i]=now++;
}
for (int i=n+3;i<2*n;i++)
{
if (now==x-1) now=x+3;
a[i]=now++;
}
}
else
{
a[n-1]=x-1,a[n+1]=x+1,a[n+2]=x-2;
int now=1;
for (int i=1;i<n-1;i++)
{
if (now==x-2) now=x+2;
a[i]=now++;
}
for (int i=n+3;i<2*n;i++)
{
if (now==x-2) now=x+2;
a[i]=now++;
}
}
puts("Yes");
for (int i=1;i<2*n;i++) printf("%d ",a[i]);puts("");
return 0;
}



【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】凌霞软件回馈社区,博客园 & 1Panel & Halo 联合会员上线
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】博客园社区专享云产品让利特惠,阿里云新客6.5折上折
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步