斯特林数与幂
参考资料：
https://www.luogu.com.cn/blog/chtholly-willem/solution-p5408
https://blog.csdn.net/guizhiyu/article/details/108336789
上升幂和下降幂
\[x^{\overline{n}}=x(x+1)...(x+n-1)
\]
\[x^{\underline{n}}=x(x-1)...(x-n+1)
\]
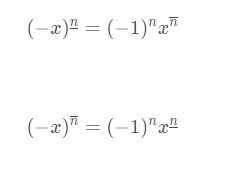
第二斯特林数
把n个有标号的球放进k个无标号的箱子里
\[S_2(n,k)=S_2(n-1,k-1)+kS_2(n-1,k)
\]
\[\sum\limits^n_{i=0}\left[\begin{matrix}n\\i\end{matrix}\right]x^i=x^{\overline{n}}
\]
考虑组合意义
\(x^n\)即为有\(x\)种颜色，\(n\)种球的方案数
枚举具体用了多少种颜色即可得到，\(x^n\)和第二类斯特林数的转化
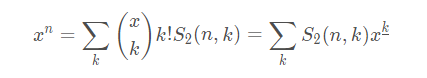
容斥有多少种颜色没用即可得到
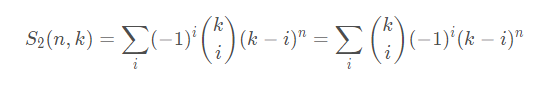
可以卷积优化得到一行的第二类斯特林数
第一类斯特林数
把n个有标号的球放进k个环里
\[S_1(n,k)=S_1(n-1,k-1)+kS_1(n-1\,k)
\]
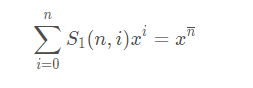
可以通过归纳法证明
通过对上升幂的倍增，可以得到一行的第一类斯特林数
原理：
\[x^{\overline{2n}}=x^{\overline{n}}(x+n)^{\overline{n}}
\]
