LOJ6212（博弈论）

 

 

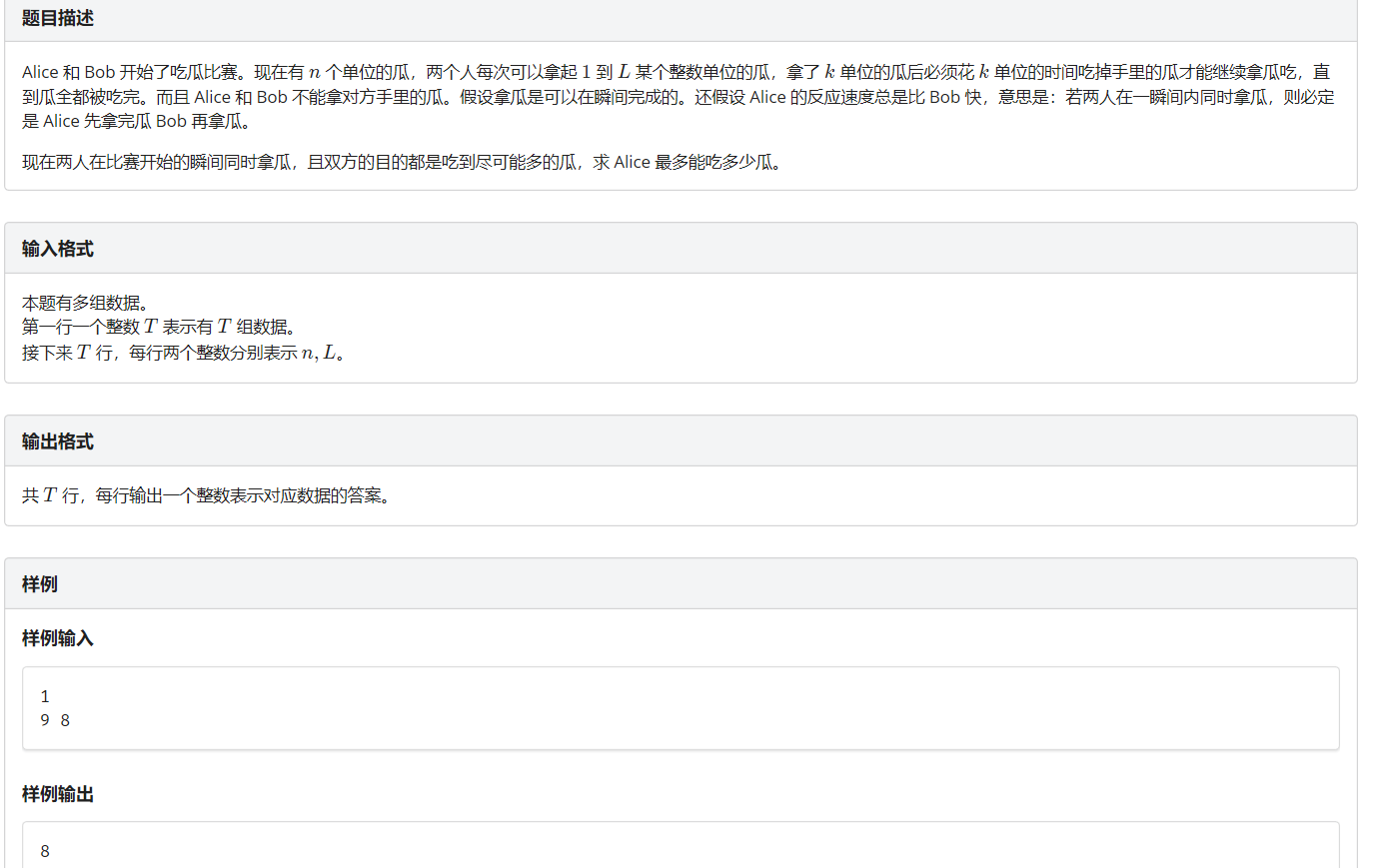
n <= L 和 n <= 2L 情况显然，一次就能取完；

分析 n > 2L 时：

Alice手速太快，Bob同学是弱势群体，所以Bob肯定不能单纯地模仿Alice，那样顶多是平手（n要是无限他俩还真就平手了）。那么他的反超策略就是：先跟着Alice，然后关键时机（瓜快没了，马上就能结束战斗）比Alice少拿一个，最后留出一分钟空闲再狠狠抓一把；

但是Alice不傻的，她不能给Bob反超的机会，所以在即将到达2L这个决胜负边界时她是要注意好分寸的，由于Bob之前一直学着她拿，一旦这次她拿多了（>1个）导致n < 2L，那Bob就可以使出“悄咪咪模仿到比Alice少1时怒抓L个”之术，这之后留给Alice的就不到L个了，Alice就败了。

鉴于二位都是明白人，所以不失一般性地，在n > 2L这段时间，不妨理解为他们的博弈就是你摸一我摸一的疯狂试探。

然后我们会发现一直拿到n == 2L时：开局时的n如果是偶数，那他们都是平手的，然后一人一大把，平局了，Alice总共吃瓜n/2个；开局时的n如果是奇数，Alice此时多拿一个，然后一人一大把结束战斗。这种情况Bob也没办法的，Alice手速快，还每次只拿一个，Bob就算多拿，Alice也能秒速跟上然后反手超过。

最后ans为Alice的吃瓜数就是ceil（n/2）了。

 

#include <cstdio>
#define ll long long
#define R(x) scanf("%lld", &x)
#define W(x) printf("%lld\n", x)

int main() {
    ll T, n, l;
    R(T);
    while (T--) {
        R(n), R(l);
        if (n <= l)
            W(n);
        else if (n <= 2 * l)
            W(l);
        else
            W((n + 1) / 2);
    }
    return 0;
}