FOJ 2200 cleaning（数学解法）

题目：

N个人围成一圈在讨论大扫除的事情，需要选出K个人。但是每个人与他距离为2的人存在矛盾，所以这K个人中任意两个人的距离不能为2，他们想知道共有多少种方法。

Input

第一行包含一个数T(T<=100)，表示测试数据的个数。

接下来每行有两个数N，K，N表示人数，K表示需要的人数(1<=N<=1000,1<=K<=N)。

Output

输出满足题意的方案数，方案数很大，所以请输出方案数mod 1,000,000,007 后的结果。

Sample Input

2
4 2
8 3

Sample Output

4
16

思路：
  现在想一想解法：
1。环形DP！！！
作者写过了，发现主要有两种方法：
1）讨论线性情况，于是发现只要讨论一下交接处即可
code：

#include<iostream>
#include<cstdio>
#include<cstring>
#include<cmath>
#include<algorithm>
#define LL long long
#define mod 1000000007
using namespace std;

LL dp[1010][1010],a[10][10];

inline int read(){
    int s=0,w=1;
    char c=getchar();
    for (;!isdigit(c);c=getchar()) if (c=='-') w=-1;
    for (;isdigit(c);c=getchar()) s=(s<<1)+(s<<3)+(c^48);
    return s*w;
}

inline void begin(){
    memset(dp,0,sizeof(dp));
    dp[1][0]=dp[1][1]=dp[0][0]=1;
    dp[2][0]=1;dp[2][1]=2;dp[2][2]=1;
    dp[3][0]=1;dp[3][1]=3;dp[3][2]=2;
    for (int i=4;i<=1000;i++){
        dp[i][0]=1,dp[i][1]=i;
        for (int j=2;j<=i;j++){
            dp[i][j]=dp[i-1][j]+dp[i-3][j-1];
            dp[i][j]%=mod;
            dp[i][j]+=dp[i-4][j-2];
            dp[i][j]%=mod;
        }
    }
    a[1][1]=1;a[2][1]=1;a[2][2]=1;
    a[3][1]=3;a[3][2]=3;a[4][1]=4;
    a[4][2]=4;a[5][1]=1;a[5][2]=5;
}

int main(){
    begin();
    int n=read();
    for (int i=1;i<=n;i++){
        int x=read(),y=read();
        if (x<6){
            printf("%d\n",a[x][y]);
        }
        else{
            LL ans=0;
            ans=ans+dp[x-2][y]+dp[x-6][y-2]*3+dp[x-5][y-1]*2;
            ans%=mod;
            printf("%lld\n",ans);            
        }
    }
    return 0;
}

2）拆环：用循环队列来极解，但作者未写过。

...

2。数学解法：

相信在座的各位大佬一定学过组合数学。这题其实可以分n的奇偶性讨论，奇数时则辗转合成一条新环，再套一下公式（竞赛书里有的，在下就不推了 懒~~）。

万能母公式：

 

 

 

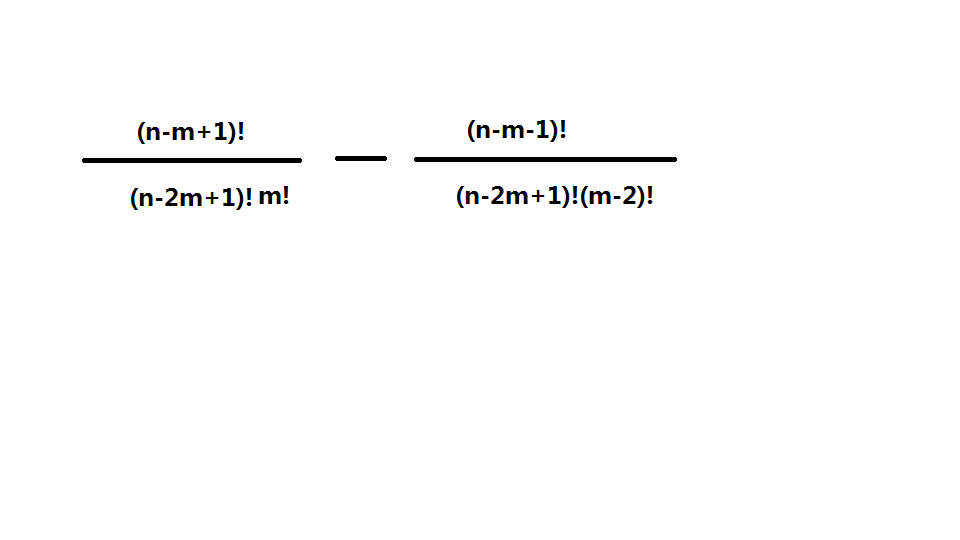
 但是好麻烦，要用到乘法逆元。

于是就想到了化简一波。

 

 

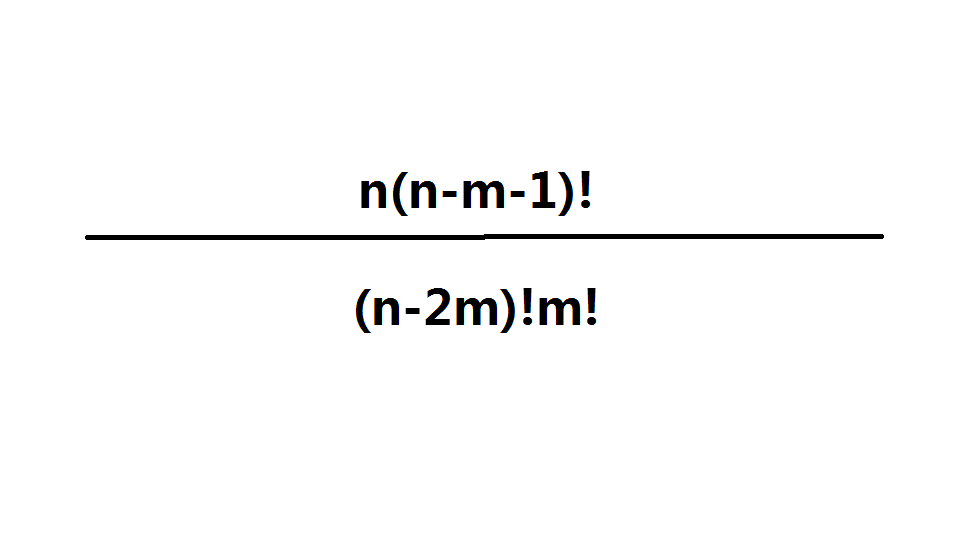
 so~~

还是不会呀。

但考虑到1000的巨弱数据，我们就想到了用唯一分解定理，化为指数运算，于是~~~

再用快速幂和桶就可以AC了！！！！

#include<iostream>
#include<cstdio>
#include<cstring>
#include<cmath>
#include<algorithm>
#define mod 1000000007
#define LL long long
using namespace std;

int a[1010],b[1010][200],fac[1010][200],cnt;

int poww(int x,int y){
    int ret=1;
    while(y){
        if(y&1) ret=1ll*ret*x%mod;
        x=1ll*x*x%mod;
        y>>=1;
    }
    return ret;
}

void Prime(int n){
    bool prime[n+10];
    memset(prime,0,sizeof(prime));
    for (int i=2;i<=n;i++){
        if (!prime[i]){
            a[++cnt]=i;
        }
        for (int j=2;j*i<=n;j++) prime[i*j]=1;
    }
    for (int i=2;i<=n;i++){
        for (int j=1;j<=cnt;j++){
            fac[i][j]=fac[i-1][j];
            if (i%a[j]==0){
                int k=i;
                while (k%a[j]==0){
                    k/=a[j],b[i][j]++,fac[i][j]++;
                }
            }
        }
            
    }
}

int get(int n,int m,int i){
    return b[n][i]+fac[n-m-1][i]-fac[n-2*m][i]-fac[m][i];
}

int main(){
    cnt=0;
    int T,n,m;
    Prime(1000);
    scanf("%d",&T);
    while (T--){
        scanf("%d%d",&n,&m);
        if (m*2>n){
            printf("0\n");
        }
        else{
            if (n%2==1){
                LL ans=1;
                for (int i=1;i<=cnt;i++){
                     int x=get(n,m,i);
                    ans*=poww(a[i],x),ans%=mod;
                }
                printf("%lld\n",ans);
            }
            if (n%2==0){
                LL ans=0;
                for (int j=0;j<=m;j++){
                    if (j>n/4||m-j>n/4) continue;
                    LL ans1=1;
                    for (int i=1;i<=cnt;i++){
                        int x=get(n/2,j,i)+get(n/2,m-j,i);
                        ans1*=poww(a[i],x),ans1%=mod;
                    } 
                    ans+=ans1,ans%=mod;
                }
                printf("%lld\n",ans);
            }
        }
        
    }
    return 0;
}