Image Processing and Computer Vision_Review：Local Invariant Feature Detectors: A Survey——2007.11

翻译

局部不变特征探测器：一项调查

摘要 -在本次调查中，我们概述了不变兴趣点探测器，它们如何随着时间的推移而发展，它们如何工作，以及它们各自的优点和缺点。我们首先定义理想局部特征检测器的属性。接下来是对过去四十年中根据不同类别的特征提取方法组织的文献的概述。然后，我们对选择的方法进行更详细的分析，这些方法对研究领域产生了特别重大的影响。最后总结并展望未来的研究方向。

1引言

在本节中，我们将讨论局部（不变）特征的本质。这个词我们的意思是什么？使用局部特征有什么好处？我们可以用它们做什么？理想的局部特征会是什么样的？这些是我们试图回答的一些问题。

1.1什么是局部特征？
局部特征是一种图像模式，它与其邻近区域不同。它通常与图像属性或多个属性的同时更改相关联，尽管它不一定完全针对此更改进行局部化。通常考虑的图像属性是强度，颜色和纹理。图1.1显示了轮廓图像（左）和灰度值图像（右）中局部特征的一些示例。局部特征可以是点，也可以是边缘或小图像块。通常，一些测量是从以局部特征为中心的区域获取并转换成描述符。然后，描述符可用于各种应用程序。

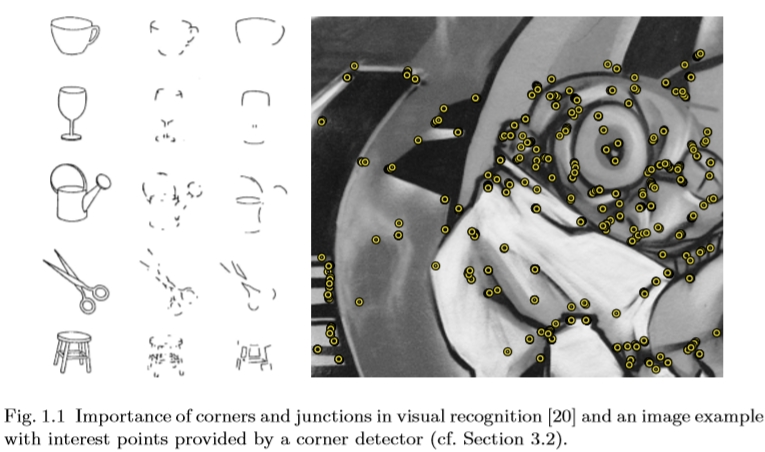
图1.1视觉识别中角点和交叉点的重要性[20]以及由角点检测器提供的感兴趣点的图像示例（参见第3.2节）。

1.2为什么局部特征？
正如前言中简要讨论的那样，局部（不变）特征是一种特征强大的工具，已成功应用于各种系统和应用程序中。
在下文中，我们基于它们的可能用途区分三大类特征检测器。它并非详尽无遗或是对探测器进行分类的唯一方法，但它强调了使用场景所需的不同属性。首先，人们可能对特定类型的局部特征感兴趣，因为它们可能在特定应用的有限上下文中具有特定的语义解释。例如，在航拍图像中检测到的边缘通常对应于道路;斑点检测可用于识别某些检查任务中的杂质;这些是已经提出局部特征检测器的第一个应用。其次，人们可能对局部特征感兴趣，因为它们提供了一组有限的良好局部化和单独识别的锚点。实际表示的特征并不是真正相关的，只要它们的位置可以准确地并且以稳定的方式随时间确定。这例如是大多数匹配或跟踪应用中的情况，尤其是用于相机校准或3D重建。其他应用领域包括姿势估计，图像对齐或镶嵌。这里的典型示例是KLT跟踪器[228]中使用的特征。最后，一组局部特征可以用作鲁棒的图像表示，其允许识别对象或场景而无需分割。同样，这些特征实际上代表什么并不重要。它们甚至不必精确地进行局部化，因为目标不是在个体基础上匹配它们，而是分析它们的统计数据。这种利用局部特征的方式首先在[213]和[210]的开创性工作中报道，并且很快变得非常流行，特别是在物体识别的背景下（对于特定物体以及类别水平识别）。其他应用领域包括场景分类，纹理分析，图像检索和视频挖掘。

显然，上述三个类别中的每一个都强加了自己的约束，并且在一个不同的问题的背景下，一个应用程序的良好特征可能是无用的。在为手头的应用搜索合适的特征检测器时，可以考虑这些类别。在本次调查中，我们主要关注第二个，尤其是第三个应用场景。
最后，值得注意的是，在人类视觉系统的物体识别环境中也证明了局部特征的重要性[20]。更准确地说，实验表明，从图像中去除角点会阻碍人类识别，而去除大部分直边信息则不会。如图1.1所示。

1.3关于术语的几点注释
在我们更详细地讨论特征检测器之前，让我们解释一下文献中常用的一些术语。

1.3.1探测器或提取器？

传统上，术语检测器已用于指代从图像中提取特征的工具，例如角点，斑点或边缘检测器。然而，这只有在事先清楚图像中的角点，斑点或边缘是什么时才有意义，因此可以说“错误检测”或“错过检测”。这仅适用于前面提到的第一种使用场景，不是最后两个，提取器可能在语义上更正确。仍然，术语检测器被广泛使用。因此，我们也坚持这个术语。

1.3.2不变量或协变量？
类似的讨论适用于“不变”或“协变”的使用。如果在从该族转换应用于其参数时其值不会改变，则该函数在某个转换族下是不变的。函数在与变换通信时是协变的，即，将变换应用于函数的参数具有与将变换应用于函数输出相同的效果。一些例子可能有助于解释这种差异。 2D表面的区域在2D旋转下是不变的，因为旋转2D表面不会使其变得更小或更大。但是，在相同的变换族中，表面的主轴惯性的方向是协变的，因为旋转2D表面将以完全相同的方式影响其主轴的方向。基于这些定义，很明显所谓的局部尺度和/或不变的特征实际上只是协变的。另一方面，由于归一化步骤，从它们派生的描述符通常是不变的。由于术语局部不变特征被广泛使用，我们在本调查中使用“不变量”。

1.3.3旋转不变或各向同性？

如果函数在所有方向上表现相同，则在特定点处是各向同性的。这个术语适用于例如纹理，不应与旋转不变性相混淆。

1.3.4兴趣点，区域或局部特征？

在某种程度上，理想的局部特征将是几何中定义的点：在空间中具有位置但没有空间范围。然而，在实践中，图像是离散的，最小的空间单位是像素，离散化效应起着重要作用。为了定位图像中的特征，需要分析局部像素邻域，为所有局部特征提供一些隐含的空间范围。对于一些应用（例如，相机校准或3D重建），在进一步处理中完全忽略该空间范围，并且仅使用从特征提取过程导出的位置（该位置有时被确定为子像素精度）。在这些情况下，通常使用术语兴趣点。

然而，在大多数应用中，还需要描述这些特征，使得它们可以被识别和匹配，并且这又需要像素的局部邻域。通常，这个邻域等于用于局部化该特征的邻域，但不一定是这种情况。在这种情况下，通常使用术语区域而不是兴趣点。但是，要注意：当使用局部像素邻域来描述兴趣点时，特征提取过程不仅要确定兴趣点的位置，还要确定该局部邻域的大小和可能的形状。特别是在几何变形的情况下，这显著地使过程复杂化，因为尺寸和形状必须以不变（协变）方式确定。
在本次调查中，我们更倾向于使用术语局部特征，它可以是点，区域甚至是边缘区段。

1.4理想局部特征的性质
局部特征通常具有空间范围，即上述像素的局部邻域。与经典分割相比，这可以是图像的任何子集。区域边界不必对应于图像外观的变化，例如颜色或纹理。而且，多个区域可能重叠，并且图像的“不感兴趣”部分（例如均匀区域）可以保持未被覆盖。

理想情况下，人们希望这些局部特征对应于语义上有意义的对象部分。然而，在实践中，这是不可行的，因为这需要对场景内容进行高级解释，这在早期阶段是不可用的。相反，探测器直接根据基础强度模式选择局部特征。

好的特征应该具有以下属性：
•可重复性：给定在不同观看条件下拍摄的同一物体或场景的两个图像，在两个图像中都可以找到在两个图像中可见的场景部分上检测到的高比例的特征。
•独特性/信息性：检测到的特征背后的强度模式应显示出很多变化，以便可以区分和匹配特征。
•局部性：特征应该是局部的，以便降低遮挡的可能性，并允许在不同观察条件下拍摄的两个图像之间的几何和光度变形的简单模型近似（例如，基于局部平面度假设）。
•数量：检测到的要素数量应足够大，以便即使在小物体上也能检测到合理数量的要素。但是，最佳特征数量取决于应用程序。理想情况下，检测到的特征的数量应该通过简单直观的阈值在大范围内适应。特征的密度应该反映图像的信息内容，以提供紧凑的图像表示。
•准确度：检测到的特征应在图像位置，尺度和可能的形状方面进行精确定位。
•效率：优选地，检测新图像中的特征应该允许对时间要求严格的应用。

可重复性，可以说是所有属性中最重要的属性，可以通过两种不同的方式实现：通过不变性或稳健性。
•不变性：当预期出现大的变形时，首选方法是在可能的情况下以数学方式对这些进行建模，然后开发不受这些数学变换影响的特征检测方法。
•稳健性：在变形相对较小的情况下，通常会使特征检测方法对这种变形不太敏感，即检测的准确性可能会降低，但不会大幅降低。使用鲁棒性解决的典型变形是图像噪声，离散化效应，压缩伪像，模糊等。通常通过包括更强的鲁棒性来克服用于获得不变性的数学模型的几何和光度偏差。

1.4.1讨论
显然，这些不同特性的重要性取决于实际的应用和设置，并且需要做出妥协。
在所有应用场景中都需要可重复性，它直接取决于其他属性，如不变性，鲁棒性，数量等。根据应用的增加或减少它们可能会导致更高的可重复性。
独特性和局部性是竞争属性，无法同时实现：特征越局部化，底层强度模式中可用信息越少，正确匹配它就越难，特别是在数据库应用程序中，有许多候选特征需要匹配至。另一方面，在平面物体和/或纯旋转相机的情况下（例如，在图像拼接应用中），图像通过全局单应性相关，并且没有遮挡或深度不连续的问题。在这些条件下，可以毫无问题地增加局部特征的大小，从而产生更高的独特性。
类似地，增加的不变性水平通常导致独特性降低，因为一些图像测量用于提升变换的自由度。类似的规则适用于鲁棒性与独特性，因为通常忽略一些信息（被视为噪声）以实现稳健性。因此，对于给定应用程序所需的不变性或稳健性水平有一个清晰的想法是很重要的。很难同时实现高不变性和鲁棒性，并且不适应应用的不变性可能对结果产生负面影响。

精确度在来自运动应用的宽基线匹配，配准和结构中尤其重要，其中需要精确对应以例如估计对极几何或校准相机设置。
数量在某些类级对象或场景识别方法中特别有用，其中密集地覆盖感兴趣的对象是至关重要的。另一方面，大多数情况下，大量特征对计算时间产生负面影响，应保持在限制范围内。稳健性对于对象类识别也是必不可少的，因为不可能在数学上对类内变化进行建模，因此不可能完全不变。对于这些应用，准确的局部化不太重要。通过具有额外的鲁棒描述符，可以抵消特征检测器的不准确定位的影响，直到某一点，这产生了不受小定位误差影响的特征向量。

1.5全局与局部特征
局部不变特征不仅允许在查看条件，遮挡和图像混乱（宽基线匹配）的大变化的情况下找到对应关系，而且还产生用于图像检索和对象或场景识别任务的图像内容的有趣描述（两者都是对于特定对象和类别）。为了将其置于上下文中，我们简要总结了一些计算图像表示的替代策略，包括全局特征，图像片段以及特征的详尽和随机抽样。

1.5.1全局特征
在图像检索领域，已经提出了许多全局特征来描述图像内容，其中颜色直方图及其变化作为典型示例[237]。这种方法效果令人惊讶，至少对于具有独特颜色的图像，只要它是用户感兴趣的整个图像的整体构图，而不是前景对象。实际上，全局特征无法区分前景和背景，并将来自两个部分的信息混合在一起。

全局特征也被用于对象识别，从而产生了第一种基于外观的方法来解决这一具有挑战性的问题。 Turk和Pentland [245]以及后来的Murase和Nayar [160]提出计算一组模型图像的主成分分析，并将投影用作前几个主成分作为描述符。与之前尝试的基于几何的纯方法相比，新颖的基于外观的方法的结果是惊人的。可以突然识别出全新的自然物体。然而，基于全局描述，图像混乱和遮挡再次形成主要问题，将系统的有用性限制于具有干净背景的情况或者可以分割对象的情况，例如，依赖于运动信息。

1.5.2图像分段
克服全局特征的限制的方法是将图像分割成有限数量的区域或片段，每个这样的区域对应于单个对象或其一部分。这种方法最著名的例子是[31]中提出的blobworld系统，它根据颜色和纹理对图像进行分割，然后在数据库中搜索具有相似“图像斑点”的图像。基于纹理分割的示例是广泛的[208]中描述的基线匹配工作。
然而，这引起了鸡与蛋的问题，因为图像分割本身是一项非常具有挑战性的任务，这通常需要对图像内容有高层次的理解。对于通用对象，颜色和纹理提示不足以获得有意义的分割。

1.5.3采样特征
处理全局特征或图像分割遇到的问题的方法是在每个位置和比例下详尽地对图像的不同子部分进行采样。对于每个这样的图像子部分，然后可以计算全局特征。该方法也称为基于滑动窗口的方法。它在人脸检测方面特别受欢迎，但也被用于识别特定对象或特定对象类，如行人或汽车。

通过关注图像的子部分，这些方法能够在查询和模型之间找到相似之处，尽管背景会发生变化，即使对象仅占整个图像区域的一小部分。在缺点方面，他们仍然无法应对部分遮挡，并且允许的形状可变性小于基于局部特征的方法可行的形状可变性。然而，到目前为止，最大的缺点是这种方法的效率低下。必须分析图像的每个子部分，从而为每个图像生成数千甚至数百个特征。这需要极其有效的方法，这些方法显著限制了可能的应用范围。

为了克服复杂性问题，使用图像块的更稀疏的固定网格采样（例如，[30,62,246,257]）。然而，难以实现这些特征的几何变形的不变性。该方法可以容忍由于在可能的位置，尺度，姿势等上进行密集采样而导致的一些变形，但是各个特征不是不变的。这种方法的一个例子是多尺度兴趣点。因此，当目标是找到图像之间的精确对应时，不能使用它们。但是，对于某些应用，例如场景分类或纹理识别，它们可能是足够的。在[62]中，在场景分类工作的背景下，使用固定的补丁网格而不是以兴趣点为中心的补丁报告更好的结果。这可以通过密集覆盖以及在固定网格方法中也考虑均匀区域（例如，天空）的事实来解释，这使得表示更加完整。这种密集的覆盖也在[66]中被利用，其中在特定对象识别的上下文中在一组局部不变特征之上使用固定的补丁网格，其中后者提供一组初始对应，然后引导为前者建立通信。

类似地，不是使用固定的贴片网格，也可以使用图像块的随机采样（例如，[97,132,169]）。这使得斑块的数量，尺度或形状的范围以及它们的空间分布具有更大的灵活性。基于随机图像块，在[132]中示出了良好的场景识别结果。与固定网格采样的情况一样，这可以通过忽略特征的定位属性的密集覆盖来解释。随机补丁实际上是密集补丁的子集，主要用于降低复杂性。它们的可重复性很差，因此它们作为常规特征的补充而不是作为独立的方法更好地工作。
最后，为了克服复杂性问题，同时仍然提供比随机定位更好的大量特征[140,146]，提出从边缘均匀地采样特征。这被证明对于处理由边和曲线很好地表示的线性物体是有用的。

1.6本次调查概述
本调查文章由两部分组成。首先，在第2节中，我们回顾了文献中的局部不变特征检测器，从计算机视觉的早期阶段到最近的演变。接下来，我们将更详细地描述一些选定的代表性方法。我们基于图像中提取的特征类型以相对直观的方式构造方法。这样做，我们区分角点检测器（第3节），斑点检测器（第4节）和区域检测器（第5节）。此外，我们添加了一个关于各种探测器的部分，这些探测器是以计算效率的方式设计的（第6节）。有了这种结构，我们希望读者能够轻松找到对他/她的应用最有用的探测器类型。我们通过对不同方法的定性比较和对未来工作的讨论来结束调查（第7节）。
对于那些不熟悉局部不变特征检测器的新手读者，我们建议首先跳过第2节。本节主要是为更高级的读者添加的，以进一步了解这个领域是如何演变的，最重要的趋势是什么，并为早期的工作添加指针。

2 文献中的局部特征

在本节中，我们概述了文献中提出的局部特征检测器，从图像处理和模式识别的早期开始到现在的最新技术。

2.1简介
关于局部特征检测的文献很多，可以追溯到1954年，当时Attneave [6]首次观察到形状信息集中在具有高曲率的主要点上。不可能详细描述50多年研究的每一项贡献。相反，我们提供了文献的指针，感兴趣的读者可以发现更多。本部分的主要目标是让读者了解所提出的各种好主意，特别是在互联网时代之前。很多时候，这些被忽视然后重新发明。我们希望对所有为当前最新技术做出贡献的研究人员给予适当的信任。

2.1.1局部特征的早期工作

重要的是要提到这个研究领域的开端以及在观察角点和交汇点在视觉识别中的重要性之后出现的第一批出版物[6]（见图1.1）。从那以后，已经提出了大量算法来提取在数字形状上计算的各种函数的极值处的兴趣点。而且，早期在图像处理和视觉模式识别领域中已经理解，直线和直角的交叉点是人造结构的强烈指示。这些特征已经用于线描图像[72]和光子学[149]的第一系列应用中。 Rosenfeld [191]以及Duda和Hart [58]及其后期版本的数字图像处理专着的第一部专着有助于建立一个完善的理论基础领域。

2.1.2概述
我们确定了许多重要的研究方向，并相应地构建了本节的各个小节。首先，许多作者研究了弯曲轮廓的曲率。他们的工作在2.2节中描述。其他人直接分析图像强度，例如，基于衍生物或具有高方差的区域。这是第2.3节的主题。另一项研究受到人类视觉系统的启发，旨在重现人类大脑的过程 - 见2.4节。第2.5节讨论了侧重于颜色信息利用的方法，而第2.6节描述了基于模型的方法。最近，存在一种趋势，即具有针对各种几何变换的不变性的特征检测，包括多尺度方法和尺度或者不变的方法。这些将在第2.7节中讨论。在2.8节中，我们关注基于分段的方法，第2.9节描述了基于机器学习技术的方法。最后，第2.10节概述了文献中提出的不同评估和比较方案。

2.2基于轮廓曲率的方法

第一类兴趣点检测器是基于轮廓曲率的方法。最初，这些主要应用于线条图，分段恒定区和cad-cam图像而不是自然场景。重点尤其是点定位的准确性。它们在20世纪70年代末和1980年代的大部分时间里最受欢迎。

2.2.1高曲率点
轮廓交叉点和交叉点通常会导致双向信号变化。因此，检测特征的良好策略包括沿高轮廓的轮廓提取点。模拟曲线的曲率定义为单位切向量相对于弧长变化的速率。轮廓通常以点链编码或使用样条以参数形式表示。

已经开发了几种技术，包括检测和链接边缘，以便通过分析链码[205]，找到曲率的最大值[108,136,152]，方向的变化[83]或变化来找到链中的角。外观[42]。其他人避免链接边缘，而是寻找曲率的最大值[254]或在渐变大的地方改变方向[104]。
在[193,195,196,197]中提出了几种基于灰度梯度和数字曲线角度变化检测边缘的方法。用于线绘图像的其他解决方案包括用于检测链编码平面曲线中的角的方法[73,74]。在这些工作中，一个点的角度的度量是基于沿链的连续段位置之间的平均角度差异。
特征提取的一种通用方法是直接通过角度或角点检测来检测主要点，使用各种方案来近似离散曲率，例如余弦[192,193]或局部曲率[18,74]，其将角定义为平均值的不连续性曲线斜率。其他参数表示如B样条曲线通常用于渲染计算机图形，压缩和编码，CAD-CAM系统以及曲线拟合和形状描述[175]中的曲线。在[108]中，三次多项式与曲线相关，并且在这种曲线中检测到不连续性以定位兴趣点。在[85]中使用线图像的样条近似与动态编程技术结合以找到样条的结。 [164]中提出了线图的伪编码和获得兴趣点的复杂矢量图。

在[207]中，基于每个点处相对于其直接邻居的局部离散曲率的迭代平均，在最大全局曲率处计算主导点。在[3]中，基于与在链码上计算的样本协方差矩阵的特征值特征向量结构相关联的几何和统计特性来定义切向偏差和离散曲线的曲率。另一种方法是获得数字曲线的分段线性多边形近似，受到对质量的限制[60,174,176]。实际上，在[174]中已经指出，具有可变断点的分段线性多边形近似将倾向于将顶点定位在实际角点处。这些点大致对应于多边形的相邻线段的实际或外推交叉点。在[91]中探讨了类似的想法。最近，[95]估计了两条线的参数与两个与角点相邻的区段。如果参数在统计上显著不同，则声明一个角。类似的方法是通过遵循图像梯度最大值或最小值并找到边缘图中的间隙来识别边缘交叉和交叉点[19]。

2.2.2处理规模
通过曲率估计的拐角检测方法通常使用一组参数来消除轮廓噪声并获得给定比例的拐角，尽管可以在多个自然尺度处找到物体拐角。为了解决这个问题，一些探测器在一定范围的参数内迭代地应用它们的算法，选择出现在一组固定迭代中的点。点的稳定性和检测所花费的时间与迭代次数密切相关。

在[207]中可以找到通过平均方案处理离散化和尺度问题的初步尝试。 [5]中提出的曲率原始草图（CPS）是沿着轮廓的曲率显著变化的尺度空间表示。这些变化被分类为基本或复合基元，例如角，平滑关节，末端，曲柄，凸起和凹痕。在不同的比例下检测特征，导致对象轮廓的多尺度表示。在[151,152]和后来的[86]中探讨了类似的想法，其中进行曲率尺度空间分析以找到局部的曲线尺度。它们在曲线的光点上找到并以参数形式表示形状。在[108,136]中也提出了基于B样条的算法。一般的想法是将B样条曲线固定到曲线上，然后直接从B样条系数测量每个点周围的曲率。

处理用于检测数字闭合曲线上的主导点的比例的另一算法[238]由来自[193]的角度检测过程激发。它们表明，主要点的检测主要依赖于支撑区域的精确确定，而不是离散曲率的估计。首先，确定基于其局部属性的每个点的支持区域。然后计算每个点的相对曲率[238]或局部对称性[170]的量度。高斯滤波器是点检测中最常用的滤波器。然而，如果高斯滤波器的比例太小，则结果可能包括一些冗余点，这些冗余点是不必要的细节，即由于噪声。如果比例太大，则支撑区域较小的点将趋于平滑。为了解决固定尺度高斯滤波中存在的问题，在[4,181]中提出了基于多尺度离散曲率表示和搜索的尺度空间过程。该方案基于稳定性标准，该标准指出拐角的存在必须与在大多数尺度下可观察到的曲率最大值一致。在[199]中研究了曲线的自然尺度，以避免在整个尺度范围内曲线的穷举表示。在[119,120]中还提出了一种成功的具有理论公式的高斯滤波器选择机制。

在[264]中，提出了一种用于临界点检测的非线性算法。他们建立了一套设计点检测算法的标准，以克服曲率近似和高斯滤波引起的问题。边界平滑的另一种方法是基于曲率估计的模拟退火[233]。在[152]中，角点位于边缘的绝对曲率的最大值处。通过多个曲率比例级别跟踪角点以改善定位。 Chang和Horng [33]提出了一种使用巢移动平均滤波器检测角点的算法[33]。通过计算模糊图像的差异并观察高曲率点的偏移来在曲线上检测角。可以在[125,199,200]中找到用于确定曲线的自然尺度的各种方法的更详细分析。

2.2.3讨论
虽然理论上在模拟曲线上有很好的基础，但在离散曲线的情况下，轮廓曲率计算的鲁棒性较差[194,238]。在[259]中研究了数字曲率估计中可能的误差源。
此外，上述探测器的目标不同于我们现在通常使用的探测器的目标。如果方法检测到圆形形状上的角点，交叉点处的多个角点等，则被认为是不利的。此时，使用了更加严格的兴趣点/角点定义，其中仅对应于3D中的真实角点的点被认为是相关的。如今，在大多数实际的兴趣点应用中，重点是稳健，稳定和独特的点，无论它们是否与真正的角点相对应（另见我们之前在1.2节中的讨论）。
由于复杂性和鲁棒性问题，最近（过去十年）该领域的活动较少，而直接基于图像强度的方法引起了更多关注。

2.3基于强度的方法
基于图像强度的方法仅具有弱假设并且通常适用于宽范围的图像。其中许多方法基于一阶和二阶灰度值导数，而其他方法则使用启发式方法找到高方差区域。

2.3.1不同的方法

基于Hessian的方法。早期基于强度的探测器之一是由Beaude提出的基于旋转不变的基于Hessian的探测器[16]。它探讨了强度表面的二阶泰勒展开，尤其是Hessian矩阵（包含二阶导数）。该矩阵的行列式达到图像中类似blob的结构的最大值。有关此方法的更详细说明，请参见第4.1节。它已在[57]和[266]中得到了扩展，其中兴趣点位于连接拐角周围的Hessian行列式的局部极值的曲线的过零点处。

类似地，可以通过计算图像表面的高斯曲率，即图像亮度中的鞍点来定位高曲率点。在[104]中，局部二次曲面与图像强度函数无关。表面参数用于确定梯度大小和梯度方向的变化率。得到的检测器使用由图像梯度缩放的二阶导数计算的等光线曲率，使其对噪声更加鲁棒。在[61,229]中提出了类似的想法。
[168,167,224]和后来的[83]中的详细研究表明，[16,57,104,163,266]的探测器都对图像执行相同的测量，并且根据基于标准的可靠性相对较低。关于局部化精度。然而，当其他特征属性变得更加重要时，Hessian矩阵的轨迹和行列式在后来成功地用于规模和兴趣点检测器[121,143]的不变扩展。
基于梯度的方法。基于fitortorder导数的局部特征检测也用于各种应用中。在移动机器人导航的背景下[154,155,156]首次介绍了在方向方差测量的局部最大值处返回点的角点检测器。它是[41]中探讨的自相关函数的启发式实现。所提出的角点检测器调查图像中的局部窗口并确定由于在各个方向上将窗口移动几个像素而导致的强度的平均变化。这个想法在[69,70]中进一步采用，并通过在所谓的第二矩矩阵中使用一阶导数来形式化，以探索方向图像强度变化的局部统计。该方法将角点候选检测和定位分开，以提高子像素精度的精度，但代价是计算复杂度更高。 Harris和Stephens [84]通过对平均强度方差进行分析扩展，改进了Moravec [155]的方法。这导致用Sobel导数和高斯窗口计算的第二矩矩阵。引入了基于该矩阵的行列式和轨迹的函数，其考虑了矩阵的特征值。这种探测器现在被广泛称为Harris探测器或Plessey探测器1，可能是最著名的兴趣点探测器。它在3.2节中有更详细的描述。它已经在许多论文中得到了扩展，例如，通过使用高斯导数[212]，一阶和二阶导数的组合[263]，或基于边缘的第二矩矩阵[45]，但基本思想保持不变。

哈里斯探测器也在[167]中进行了研究，并证明对于L结是最佳的。基于ffine图像变形的假设，[228]中的分析得出结论：使用自相关矩阵的最小特征值作为角强度函数更方便。
最近，基于尺度空间理论[115,117]，第二矩矩阵也被采用来通过参数化高斯滤波器并根据比例对其进行归一化来改变变化[59]。此外，哈里斯探测器在[13,142,209]中使用拉普拉斯算子和第二矩矩阵的特征值在[13,142,209]中进行了扩展搜索，其灵感来自于林德伯格的开创性工作[117,118]（参见章节） 3.4详情）。
来自[263]的方法执行对第二矩矩阵及其近似的计算的分析。通过仅计算两个平滑图像而不是先前所需的三个图像来实现速度增加。关于如何从二阶矩阵[84,101,167,228]计算角部强度已经提出了许多其他建议，并且这些已经被证明等同于各种矩阵规范[102,265]。在[102]中也提出了对具有多维像素的图像的推广。

在[242]中，Harris角点检测器被扩展为在比纯翻译更一般的变换下产生稳定的特征。为此，在旋转，缩放，直到完全变换的情况下研究自相关函数。

2.3.2强度变化
基于强度变化的不同类别的方法应用数学形态学来提取高曲率点。在[36]中研究了使用形态学开放算子检测到的二元图像中形状边界曲率的零交叉。数学形态学也用于从[107,114,168]中的边缘提取凸点和凹点。后来在[262]中提出了一种基于形态残差和角点特征分析的并行算法。
另一种方法[173]表明，对于兴趣点，小邻域的中值与角点值明显不同。因此，中心和中位数之间强度的差异给出了角点的强烈指示。但是，此方法无法处理更复杂的连接或平滑边缘。
根据[82]的早期工作，在[232]中引入了一个简单而有效的探测器SUSAN。它计算邻域内与中心像素强度相似的像素分数。然后可以通过对该度量进行阈值处理并选择局部最小值来对角进行定位。重心的位置用于消除误报。有关SUSAN探测器的更多详细信息，请参见第3.3节。在[112,240]中探讨了类似的想法，其中考虑了圆上的像素并将其与贴片的中心进行比较。
最近，[203]提出了FAST检测器。如果可以在点周围的固定半径圆周上找到一组足够大的像素，使得这些像素比中心点明显更亮（相对更暗），则将点分类为角。高效的分类基于决策树。有关FAST的更多详细信息，请参见第6.3节。

在[127]中已经探索了局部径向对称来识别兴趣点，并且还提出了其实时实现。在特征点提取的背景下，还研究了小波变换，并在[35,111,218]中基于多分辨率分析获得了成功的结果。

2.3.3显著性
显著性的概念已被用于许多计算机视觉算法中。使用边缘检测器来提取对象描述的早期方法体现了边缘比图像的其他部分更显著的想法。对显著性的更明确的使用可以分为专注于低级局部特征的那些（例如，[215]），以及那些计算低级特征的显著分组的那些（例如，[223]）;虽然有些方法在两个层面都有效（例如，[147]）。
[211]中提出的技术基于特定图像上的描述符向量的最大化。这些突出点是物体上几乎唯一的点。因此，它们最大化了对象之间的区别。相关方法[253]识别用于自动生成统计形状/外观模型的显著特征。该方法旨在选择那些不太可能不匹配的特征。从图像生成的多维特征空间中的低密度区域被分类为非常突出。
在[79]中提出了一种基于区域内图像强度的可变性或复杂性的理论上更成熟的方法。它受到视觉显著性和信息内容的推动，我们将在下一节进行修订。 [79]的方法在局部信号复杂性或不可预测性方面决定了显著性;更具体地说，建议使用局部属性的Shannon熵。我们的想法是找出一个高度复杂的点邻域作为显著性或信息内容的度量。该方法测量在点邻域中计算的灰度值直方图的熵的变化。搜索扩展到比例[98]和ffine [99]参数化区域，从而提供区域邻域的位置，比例和形状。有关详细讨论，请参阅第4.3节。

2.4生物学上可行的方法
前面部分提出的大多数系统主要关注兴趣点定位的准确性。这在将参数曲线设置为控制点或图像匹配以恢复几何图形的背景下非常重要。相比之下，本节回顾的生物学合理方法主要是在人工智能和视觉识别的背景下提出的。他们中的大多数没有特定的应用目的，他们的主要目标是模拟人类大脑的过程。在认知心理学和计算机视觉中已经讨论了许多人类视觉注意力或显著性模型。然而，绝大多数只是理论上的兴趣，只有少数在实际图像上实施和测试。

2.4.1特征检测作为预注意阶段的一部分
归因于Neisser [165]，人类早期视觉的主要模型之一是它包含一个预先注意力和注意力的阶段。用于特征检测的生物学上合理的方法通常指的是场景的某些部分在人类视觉系统的早期阶段具有预先注意力的特征并且产生某种形式的即时响应的想法。在预注意阶段，仅检测到“弹出”特征。这些是图像的局部区域，其呈现某种形式的空间不连续性。在关注阶段，找到这些特征之间的关系，并进行分组。该模型广泛影响计算机视觉社区（主要通过Marr [133]的工作），并反映在经典的计算机视觉方法 - 特征检测和感知分组，其次是模型匹配和通信搜索。在神经生理学和心理学研究取得进展之后，关注模型中的活动开始于20世纪80年代中期。

[87,198]提出了一种受神经生物学机制启发的方法。他们使用类似过滤器的Gabor来计算信号的局部能量。该能量的一阶和二阶导数的最大值表示存在兴趣点。在[131,186]中进一步探讨了使用来自不同尺度的Gabor滤波器响应的想法。 [182]中提出的方法是由心理物理实验推动的。它们计算每个图像像素在不同方向上的信号的对称分数。然后选择具有显著对称性的区域作为兴趣点。

[96]中介绍了纹理识别理论和文本作为简单局部结构（如斑点，角点，交汇点，线端等）的概念。他认为，关于纹理分布的统计数据在识别中起着重要作用。简单文本的提取是在预注意阶段和关注阶段的关系构建中完成的。在[241]中提出了基于这些原理的特征整合理论。他将区别特征可以直接定位在特征图中的析取案例和仅通过同时处理各种特征图来提取特征的联合案例区分开来。该模型通过结合自下而上和自上而下的感兴趣测量来实现[32]。自下而上方法合并各种要素图并查找有趣事件，而在自上而下过程中，利用有关目标的知识。
上述系统的主要目标是提供计算上可信的视觉注意模型。他们的兴趣主要是理论。然而，一旦神经网络等机器学习技术变得足够成熟，这些系统就成为真实图像实用解决方案的灵感来源。在[206]中，图像处理操作符与注意力模型相结合，使其适用于更逼真的图像。他将拉普拉斯高斯（LoG）运算符应用于特征映射，以对接收场进行建模并增强有趣事件。在多个尺度上分析图像。来自[78]的方法使用一组特征模板并将它们与图像相关联以产生特征图，然后用LoG增强特征图。时间导数用于检测移动物体。

Koch和Ullman [105]提出了一种非常具有视觉注意力的计算模型，它解释了几种心理物理现象。他们提出建立一组基于方向，颜色，视差和运动的地图，并通过提取与其邻域明显不同的位置来模拟横向抑制机制。然后将来自不同地图的信息合并到单个显著图中。使用赢家通吃（WTA）网络使用金字塔策略以分层方式选择地图中的活动位置。 [105,241]中提出的假设首先在[34]中实现。在[49]中提出了类似的WTA模型实现。

在[223]中通过对诸如轮廓片段之类的局部信息进行分组来研究诸如物体轮廓之类的全局显著结构的提取，但是没有涉及预注意视觉。

2.4.2非均匀分辨率和粗到细处理
在生物学上合理的模型中也研究了视网膜的非均匀分辨率和粗到细处理策略。这些主要通过尺度空间技术[9,10,187,255]进行模拟。然而，这些系统主要集中在工程和实时方面，而不是生物学上的合理性。在[27]中提出了在尺度空间中执行兴趣点检测的第一个系统之一。他们建立了一个拉普拉斯金字塔，用于粗略到特征选择。模板用于局部化LoG空间中的对象。模板也被用于构建特征图，然后通过加权和[39]进行组合。在[76]中设计的系统中使用了高斯（DoG）滤波器来加速计算。
在[81]中开发的生物启发系统探索了使用基于DoG滤波器的边界和兴趣点检测器以及设置高斯（DOOG）的方向性差来模拟V1中的简单单元的想法。

[130]中提出的系统主要涉及[96]早期研究的纹理分类。特征提取部分使用基于定向内核（DoG和DOOG）的一组过滤器来生成类似于[81]的特征映射。下一阶段对应于WTA机制，以抑制弱反应和模拟横向抑制。最后，合并所有响应以检测纹理边界。

2.4.3空间事件检测
稳健的统计数据也被用于检测一组图像基元中的异常值。这个想法是基于这样的观察：纹理可以用它们的统计数据来表示，违反这些统计数据的位置代表有趣的事件。例如，纹理基元在[148]中使用直方图和RANSAC由许多属性表示。
在[23]中使用了在不同尺度下从DoG的零交叉计算的特征图的一阶统计量。对于每个点，然后构建梯度方向的直方图，并且将局部直方图组合成全局的直方图，其在精神上与更近的SIFT描述符[124,126]类似。然后将局部直方图与全局直方图进行比较以提供感兴趣的度量。
在[172]中提出了另一种统计模型。它们测量距感兴趣点的距离范围内的边缘密度，以构建边缘分布直方图。这个想法后来在[17]的形状上下文描述符中使用。
在[92]中首先发现了仅对在其接受场内终止的边缘和条形作出反应的细胞。在[87,260]中提出了一种基于视觉皮层中这种终止细胞模型的角点检测算法。此外，基于颜色对手过程，以生物学上合理的方式将终止细胞的概念推广到颜色通道[260]。
最新的视觉注意系统也受早期灵长类视觉系统的推动，见[94]。在局部空间不连续处检测到的强度，颜色和方向的多尺度图像特征被组合成单个地形显著图，并且神经网络根据显著性选择位置。

可以在[162,221,222]中找到遵循来自[185]的模型的视觉皮层V1的其他视觉识别系统。这些方法试图从视觉皮层实现简单和复杂的细胞，这些细胞是多尺度Gabor和edgel检测器，然后是局部最大值选择方法。

2.5基于颜色的方法
颜色提供可用于特征提取过程的其他信息。在上一节中回顾的几种生物学上可行的方法使用颜色来构建显著图[93,94,105,260]。
鉴于哈里斯角的高性能[84]，在[80,153]中引入了第二矩矩阵到RGB颜色空间的直接扩展，在Harris角提取过程中引入了颜色信息。
在[250]中提出了基于颜色显著性的突出点检测。显著点是显著性图的最大值，它表示点邻域中颜色衍生物的独特性。在相关工作[217]中，他们认为基于颜色的突出点的独特性远高于强度突出点。相邻像素之间的颜色比用于获得与照明无关的衍生物，这导致对照明变化更稳健的颜色兴趣点。基于颜色的大多数提出的方法是基于强度变化的方法的简单扩展。颜色梯度通常用于增强或验证强度变化，以便增加特征检测器的稳定性，但像素强度仍然是特征检测的主要信息源。

2.6基于模型的方法

已经有一些尝试通过基于差异几何技术[82]或轮廓曲率[53]给出图像中角点的形式表示来进行角点检测的分析研究。例如，发现灰度角点可以作为最陡的灰度斜率线上的最大平面曲率点[82,188]。在[180]中研究了最佳函数的解析表达式，其中图像的卷积在角点具有显著的值。

[82,201]中提出的方法假设一个角类似于模糊的楔形，并通过将其设置为局部图像来找到楔形的特征（振幅，角度和模糊）。在[188]中使用了多个多边结的模型。假设结是由均匀区域形成的。参数化掩模用于确定强度结构，包括位置，方向，强度，模糊和边缘。然后在检测期间使残余物最小化。如果参数的良好初始化，精度很高。通过使用不同的模糊函数和初始化参数的方法，在[52]中改进了[188]中方法的效率。在[137,171]中也考虑了将角模型拟合到图像数据。对于每个可能的线的交叉点，基于假设角的角度，方向和比例来构造模板。然后将模板与感兴趣点的小邻域中的图像匹配以验证模型。在[128]中还描述了一种用于定位鞍点的基于模板的方法，其中角点对应于鞍脊和鞍谷结构的交叉点。

在[113]中建立了一组轮廓点的模糊模式，并且角点检测被表征为模式的模糊分类问题。

在[54,266]中提出了其他基于模型的方法，旨在提高基于Hessian的角点检测器的检测精度[16]。为此，分析了角点探测器对尺度空间理论模型的响应。据观察，操作员在不同尺度上的响应沿着平分线移动。值得注意的是，这种观察对于流行的Harris角点探测器也是有效的[84]。然后根据两个响应计算拐角的确切位置，这两个响应指示平分线及其与拉普拉斯响应的过零点的交点。还使用了一个ffine变换来对图像进行角点模型[22]。

在[77]中提出了一种不同的基于模型的方法。对于每种类型的特征，开发参数模型以表征图像中的局部强度。将强度分布投影到一组正交Zernike矩生成多项式上用于估计模型参数并生成特征图。

一种有趣的技术是通过使用广义霍夫变换[51,226]来设置参数化模型来找到角点。在具有提取边缘的图像中，每个角点的参数空间中出现两条线，并且峰值出现在交叉处。在[229]中考虑了模板形式的真实角模型。应用了相似性度量和几种替代匹配方案。通过合并不同匹配技术的输出，提高了检测和定位精度。
通常，在上述方法中仅考虑相对简单的特征模型，并且对多边形以外的图像的推广不明显。复杂性也是这种方法的主要缺点。

2.7走向视点不变方法
到目前为止所描述的大多数探测器以单一尺度提取特征，由探测器的内部参数确定。在20世纪90年代末，随着局部特征越来越多地用于广泛的基线匹配和物体识别，人们越来越需要能够应对尺度变化或甚至更普遍的视点变化的特征。

2.7.1多尺度方法
到目前为止所描述的大多数探测器以单一尺度提取特征，由探测器的内部参数确定。为了处理尺度变化，一种简单的方法包括在一系列尺度上提取点并将所有这些点一起使用来表示图像。这被称为多尺度或多分辨率方法[48]。

在[59]中，提出了哈里斯算子的尺度改编版本。在多个尺度上应用的Harris函数的局部最大值处检测兴趣点。由于使用归一化导数，对于在不同尺度下检测到的点，获得了相当的角度测量强度，使得可以使用单个阈值来拒绝所有尺度上较少的重要角点。这种适应规模的探测器显著提高了尺度变化下兴趣点的可重复性。另一方面，当给出关于两个图像之间的比例变化的先验知识时，可以调整检测器以便仅在所选择的比例下提取兴趣点。这产生了一组点，对于这些点，相应的定位和比例完美地反映了图像之间的实际尺度变化。

一般而言，多尺度方法可以解决与特征密集采样相同的问题（参见第1.5节）。它们不能很好地应对在一系列尺度上存在局部图像结构的情况，这导致在该范围内的每个尺度处检测到多个兴趣点。因此，有许多点代表相同的结构，但具有稍微不同的定位和规模。大量的点增加了匹配和识别的模糊性和计算复杂性。因此，在算法的进一步步骤中，需要用于选择精确对应和验证结果的有效方法。与来自运动应用的结构相比，这在识别的上下文中不是问题，其中单个点可以具有多个正确的匹配。

2.7.2尺度不变的探测器
为了克服许多重叠检测的问题，典型的多尺度方法，已经引入了尺度不变的方法。这些会自动确定局部特征的位置和比例。在这种情况下，特征通常是圆形区域。
许多现有方法在图像的3D表示（x，y和scale）中搜索最大值。这种在尺度空间中检测局部特征的想法是在20世纪80年代早期引入的[47]。金字塔表示用低通滤波器计算。如果特征点处于周围3D立方体的局部最大值并且其绝对值高于某个阈值，则检测该特征点。从那时起，已经提出了许多用于在尺度空间中选择点的方法。现有方法主要不同于用于建立尺度空间表示的差异表达式。

在[116,120]中应用归一化的LoG函数来构建尺度空间表示并搜索3D最大值。通过用增加大小的高斯核的导数平滑高分辨率图像来构建尺度空间表示。通过在比例空间中选择局部最大值来执行自动比例选择（参见第3.4节）。 LoG算子是圆对称的。因此，旋转自然是不变的。它也适用于检测斑点状结构。 [138]中的实验评估显示该特征非常适合自动比例选择。 [24]也探讨了具有自动尺度选择的兴趣点探测器的尺度不变性。在[24]的组合框架中还提出了具有自动尺度选择的角点检测和斑点检测，用于特征跟踪，适应空间和时间尺寸变化。针对局部化而优化的兴趣点标准不必与用于优化量表的兴趣点标准相同。在[138]中，引入了尺度变化的角点检测器，压痕Harris-Laplace和尺度不变的斑点检测器，创造了Hessian-Laplace。在这些方法中，位置和比例被迭代更新直到收敛[143]。更多细节可以在3.4和4.2节中找到。
在[126]中介绍了一种基于DoG滤波器构建的尺度空间金字塔中基于局部三维极值的目标识别的高效算法。金字塔表示中的局部3D极值确定了兴趣点的定位和尺度。该方法将在6.1节中进一步讨论。

2.7.3一个不变的方法
一个不变的不变量检测器可以看作是尺度不变的检测器对非均匀缩放和偏斜的概括，即在两个正交方向上具有不同的缩放因子并且没有保持角度。非均匀缩放不仅影响定位和尺度，还影响特征局部结构的形状。因此，在显著变换的情况下，尺度不变的检测器失效。

在过去[50,90,204]中经常提到一种不变的特征检测，匹配和识别。在这里，我们专注于处理不变兴趣点检测的方法。
一类方法涉及在ffine和透视变换下的定位精度。在[2]中提出了一种用于角定位的ffine不变算法，该算法建立在[54]中的观察上。应用ffine形态多尺度分析来提取角点。角的演变由线性函数给出，该线性函数由检测点与真实角的距离和距离形成。基于多尺度点沿平分线移动并且角度指示真实位置的假设来计算拐角的位置和方向。然而，在自然场景中，角点可以采取任何形式的双向信号变化，并且在实践中，点的演变很少遵循平分线。因此，该方法的适用性限于类似多边形的世界。
其他方法涉及同时检测局部结构的位置，大小和形状。 [247]中介绍的方法，铸造的EBR（基于边缘的区域）从哈里斯角和附近的交叉边开始。沿着边缘移动的两个点与Harris点一起确定平行四边形。这些点停在平行四边形所覆盖的一些光度量纹理到达极值的位置。该方法可以归类为基于模型的方法，因为它在图像中寻找特定的结构，尽管不像2.6节中描述的大多数方法那样严格。更多细节可以在第3.5节中找到。在[12]中已经探索了类似的方案。

在[248]中也提出了基于强度的方法（IBR，基于强度的区域）。它始于提取局部强度极值。研究了从局部极值发出的光线的强度分布。在该地方的每条射线上放置一个标记，其中强度分布显著变化。最后，将椭圆固定到由标记确定的区域。该方法将在5.1节中进一步讨论。在精神上有点相似的是[134]中提出并在下一节中描述的最大稳定极值区域或MSER。

在[121]中，在纹理形状的背景下，引入了使用迭代方案找到类似blob的不变特征的方法。基于形状适应固定点的不变性的该方法也用于估计来自双目数据的表面取向（来自视差梯度的形状）。该算法探索了第二矩矩阵的性质，并迭代估计局部模式的变形。它有效地估计了将补丁投影到第二矩矩阵的特征值相等的帧的变换。这项工作为其他几种不变的探测器提供了理论背景。
它与Harris角点检测器结合使用，用于[13]中的匹配，[109]中的手跟踪，指纹识别[1]以及[208]中纹理区域的完整再现。在[13]中，使用Harris检测器在几个尺度上提取兴趣点，然后使用来自[118]的迭代过程使区域的形状适应于局部图像结构。这允许为给定的固定尺度和位置提取ffine不变描述符 - 也就是说，点的比例和位置不是以不变的方式提取的。此外，多尺度Harris检测器提取在相邻尺度水平重复的许多点。这增加了不匹配的可能性和复杂性。
[141]中引入的Harris-Laplace检测器在[142,209]中通过[13,118,121]中提出的算法进行了归一化。该检测器具有相同的缺点，因为点的初始位置和比例不是以不变的方式提取的，尽管视图之间的均匀比例变化由尺度不变的Harris-Laplace检测器处理。

超越了变革。在[236]中引入了一种甚至超出了ffine变换并且对于投影变换不变的方案。然而，在局部范围内，视角效应通常是可以忽略的。更具破坏性的是非平面性或非刚性变形的影响。这就是为什么在[251]中基于等价类的定义提出了将局部特征的使用扩展到非平面表面的理论框架。然而，在实践中，它们仅在直角上显示结果。同时，通过在3D空间中嵌入图像作为2D表面并利用测地距离，在[122]中开发了对于一般变形不变的方法。

2.8基于分段的方法
在特征提取的背景下也采用了分割技术。这些方法或者应用于找到均匀区域以定位其边界上的连接点，或者直接将这些区域用作局部特征。对于通用特征提取问题，考虑了大多数基于低级像素分组的自下而上分割，尽管在某些特定任务中也可以应用自上而下的方法。尽管在分割问题的分析和形式化方面已经取得了重大进展，但在一般情况下仍然是一个未解决的问题。由于可能的特征点组的大搜索空间，特别是在基于多个图像提示的算法中，最佳分割通常是难以处理的。此外，即使对于同一图像，多种最佳分割的定义也使得它难以解决。尽管如此，已经开发了几种使用基于分割的兴趣区域的系统，尤其是在检索，匹配和识别的背景下。
在计算机视觉的早期，图像的多边形近似在场景分析和医学图像分析中很受欢迎[9,25,58]。这些算法通常涉及边缘检测和后续边缘跟踪以进行区域识别。在[63,64]中，图片的顶点被定义为在三个或更多个分段区域中共同的那些点。它可以被视为使用分割提取兴趣点的第一次尝试之一。在[123]中使用将贴片简单分割成两个区域，并将区域与第一个角进行比较。不幸的是，这两个区域的假设使得该方法的有用性受到限制。

另一组方法通过分割来表示真实图像[129]。表现良好的图像分割方法基于图形切割，其中图形表示连接的图像像素[21,75,225,227]。这些方法允许以所需的细节水平获得分割。尽管语义分割不可靠，但过度分割图像可以产生许多与对象相关的区域。这种方法在[31,46]中进行了探索，它对图像检索问题特别有吸引力，其目标是通过具有相似属性的区域找到相似的图像。在[44]中，目标是创建关注均匀区域的兴趣运算符，并计算这些区域的局部图像描述符。使用基于内核的优化方法在多个特征空间上执行分割。这些区域可以单独描述并用于识别，但它们的独特性很低。这个方向最近引起了更多的兴趣，一些方法使用自下而上的分割来提取感兴趣区域或所谓的超像素[159,184]（另见第5.3节）。

通常，该表示的缺点在于分割结果仍然不稳定并且不足以处理大量图像。在[134]中采用了成功解决这些问题的方法。使用分水岭分割算法提取最大稳定极值区域（MSER）。该方法提取在宽范围的阈值内稳定的均匀强度区域。然后用具有相同形状的椭圆替换这些区域，直到二阶。最近，在[177]中引入了该方法的变体，其通过使用区域等照度来处理模糊区域边界的问题。从某种意义上说，这种方法也类似于5.1节中描述的IBR方法，因为提取了非常相似的区域。有关MSER的更多详细信息，请参见第5.2节。该方法在[56,161]中进行了扩展，其中树状表示图像中的分水岭演化。

2.9基于机器学习的方法
机器学习领域的进步和可用计算能力的增加允许学习技术进入特征提取域。从训练示例中学习局部特征的属性然后使用该信息来提取其他图像中的特征的想法已经在视觉社区中存在了一段时间，但直到最近它才更广泛地用于实际应用中。这些方法的成功归因于这样一个事实，即由分类器提供的效率变得比检测精度更令人满意。

在[37,55]中，训练神经网络以识别边缘在一定程度上靠近图像块中心的角点。这适用于边缘检测后的图像。 [244]中探讨了类似的想法，以提高数字曲线曲率测量的稳定性。
决策树[178]也已成功用于兴趣点检测任务。在[202,203]中采用了在中心点和相邻点[173,232,240]之间使用强度差异的想法。他们构建了一个决策树，将点邻域分为角点[203]。他们的工作主要关注的是测试许多可能差异中的一小部分的效率，并且树经过培训以优化它。 [203]的方法也扩展了LoG滤波器以检测[112]中的多尺度点。他们使用基于个体兴趣点在透视投影图像上的可重复性的特征选择技术。
[11]中描述了一种混合方法，它集成了遗传算法和决策树学习，以便提取识别复杂视觉概念的辨别特征。在[243]中，兴趣点检测被提出作为优化问题。他们使用基于遗传编程的学习方法构建运算符以提取特征。学习兴趣点算子的问题是在[103]中提出的，其中人眼运动被研究以找到固定点并训练SVM分类器。
可以容易地将特征检测问题概括为分类问题，并且对由一个或多个经典检测器的组合提供的图像示例训练识别系统。任何机器学习方法都可以用于此。在[15]中使用Haar类似于使用积分图像实现近似多尺度导数的滤波器。

自然延伸将使用Viola和Jones [252]的学习方案成功应用于人脸检测，以便有效地对兴趣点进行分类。基于机器学习的方法在定位，尺度和形状估计方面的准确性通常低于通用检测器[84,134,143]，但在物体识别的背景下，效率通常更有益。

2.10评估
鉴于众多兴趣点方法，早期就确定了对独立绩效评估的需求，并且在过去三十年中已经进行了许多实验测试。使用了各种实验框架和标准。 [205]中提出了基于链编码曲线的角点检测技术的第一次比较。在早期的论文中，通常只进行目视检查[104]。其他人进行了更多的定量评估，为单个图像或小测试数据提供分数[57,266]。
角点探测器通常在人工生成的图像上进行测试，这些图像具有不同角度，长度，对比度，噪声，模糊等不同类型的交叉点[41,179]。使用不同的光度和几何变换来生成测试数据并评估[37,100,124,128]中的角点检测器。这种方法简化了评估过程，但无法对在实际应用场景中影响探测器性能的所有噪声和变形进行建模，因此性能结果往往过于乐观。在[150]中采用了一种不同的方法。在那里，性能比较被认为是一般的识别问题。角度在变换后的图像上手动注释，并且使用类似于检测率和召回的一致性和准确度等度量来评估检测器。

在[88]中，从多面体对象中提取点集，并且使用投影不变量来计算对角的坐标的约束。他们估计从点坐标到该流形的距离的方差，与相机参数和物体姿态无关。非线性差分用于消除噪声，[188]的方法比[104]中提出的方法更好。在[40]中也研究了使用平面不变量的想法来评估基于边缘的角点探测器。特征的理论特性和定位精度也在[54,88,188,189,190]中基于参数L角进行了测试。模型来评估定位精度。此外，一个随机的角点生成器已被用于测试定位误差[261]。

在[238]中评估了现有技术的基于曲线的探测器[3,74,193,197,207]。检测到的主要点的质量的定量测量被定义为数字曲线和从兴趣点近似的多边形之间的逐点误差。所报告的尺度调整方法的性能比其他方法更好。
重复率和信息含量测量在[83]中介绍。如果它有两个主要特性，它们会认为图像中的一个点很有趣：独特性和不变性。这意味着一个点应该与其直接邻居区分开来。此外，关于预期的几何和辐射畸变，兴趣点的位置和选择应该是不变的。从一组被调查的探测器[57,84,104,232,266]，Harris [84]和后来描述为SUSAN [232]的角点表现最佳。
在[215]中进行了基于重复性和由描述符的熵测量的信息内容的几个兴趣点检测器的系统评估。评估表明，修改后的Harris探测器可以在具有不同几何变换的图像对上提供最稳定的结果。在[218]中还评估了图像检索环境中的重复率和信息含量，以表明基于小波的凸点提取算法优于Harris检测器[84]。
在[43]中引入了角点数和精度标准的一致性作为评估标准。这克服了有利于提供更多特征的检测器的可重复性标准的问题。相反，引入的标准有利于提供相似数量的点的检测器，而不管物体变换如何，即使图像中的细节数量随着比例和分辨率而变化。将几个检测器[84,104,152,232]与为[152]的修改实现报告的最佳性能进行比较。

跟踪和在跟踪期间检测到角的帧数用于比较[239,240]中的检测器。同样Bae等人。 [8]使用相关和匹配来找到帧之间的重复角点，并将它们的数字与参考帧进行比较。
在[144,145]中已经对常用的特征检测器和描述符进行了广泛的评估。对不同几何变换相关的平面场景的图像对的可重复性计算了不同的现有技术规模和一个不变的检测器。基于分水岭分割的MSER区域检测器[134]在各种结构化场景中表现出最高的准确性和稳定性。 Mikolajczyk和Tuytelaars [145]收集的数据成为评估兴趣点探测器和描述符的标准基准.2

2见http://www.robots.ox.ac.uk/~vgg/research/a ffine。

最近，在[71,157,158]中，在跨越视点和照明条件匹配3D对象特征的背景下，已经研究了来自[144,145]的特征检测器和描述符的性能。基于交叉极线约束的方法自动提供地面实况对应。在这次评估中，[143]中介绍的ffi不变检测器对视点变化最为稳健。来自[124]的DoG探测器在基于自然3D场景图像的类似评估中被报道为最佳[256]。

还使用对象类别训练数据在[99,139,235]的识别环境中评估特征检测器，其中直接对应不能自动验证。在[139]中测量了聚类特性和特征聚类的紧凑性。一些特定的识别任务，如行人检测也被用来比较[220]中不同特征的表现。

3 角点探测器

在文献中已经提出了大量的角点检测器方法。为了引导读者找到适合于给定应用的方法，已经基于基础提取技术（例如，基于图像导数，形态或几何）以及基于不变性水平（翻译）选择了代表性方法。和旋转，缩放或不变量。对于每个类别，我们描述了一些最佳性能和代表性方法的特征提取过程。

3.1简介
重要的是要注意，这里使用的术语角有一个特定的含义。检测到的点对应于具有高曲率的2D图像中的点。这些不一定对应于3D角的投影。在各种类型的连接处，高度纹理化的表面，遮挡边界等处发现角。对于许多实际应用，这是足够的，因为目标是具有一组稳定且可重复的特征。这些是否是真正的角点被认为是无关紧要的。

我们从基于衍生物的方法开始本节，Harris角点检测器，在3.2节中描述。接下来，我们解释SUSAN探测器的基本思想（第3.3节），这是一个基于高效形态学算子的方法的例子。然后我们继续研究具有更高水平不变性的探测器，从Harris探测器的尺度和不变的扩展开始：Harris-Laplace和Harris-A ffine（3.4节）。接下来是第3.5节中对EdgeBased区域的讨论。最后，我们以简短的讨论结束本节（第3.6节）。

3.2哈里斯探测器
Harris和Stephens [84]提出的Harris探测器基于第二矩矩阵，也称为自相关矩阵，通常用于特征检测和描述局部图像结构。该矩阵描述了点的局部邻域中的梯度分布：

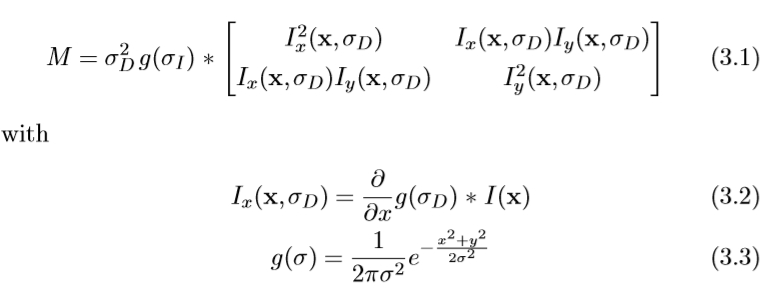
用具有尺度σD的高斯核（the differentiation scale 差异量表）计算局部图像导数。然后通过用高斯尺度窗σI（积分尺度）平滑，在该点附近对导数进行平均。该矩阵的特征值表示在由σI定义的点周围的邻域中的两个正交方向上的主要信号变化。基于该属性，可以找到角点作为图像中图像信号在两个方向上显著变化的位置，或者换句话说，两个特征值都很大。在实践中，Harris建议对角度使用以下度量，它将两个特征值组合在一个度量中并且计算成本更低：

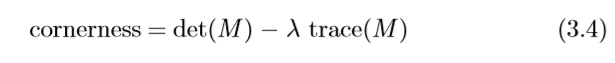
用det（M）表示行列式和trace（M）表示矩阵M的迹，λ的典型值是0.04。由于矩阵的行列式等于其特征值的乘积并且迹线对应于和，因此很明显，角度度量的高值对应于两个特征值都很大。使用迹线添加第二项会降低操作员对强直线轮廓的响应。此外，基于行列式和轨迹计算该度量在计算上要比实际计算特征值要求低。这似乎现在不那么重要了，但是在1988年，当计算资源仍然非常有限时，它很重要。

角提取过程的后续阶段如图3.1所示。给定原始图像 I（x，y）（左上），第一步包括计算一阶导数 Ix 和 Iy（左下）。接下来，获取这些梯度图像的产物（右下）。然后，用高斯核对图像进行平滑处理。这些图像包含Hessian矩阵的不同元素，然后按照公式（3.4）（右上角）将最终步骤组合成角度度量。

图3.1第二矩矩阵和Harris角度测量的分量图。

当用作兴趣点检测器时，使用非最大抑制来提取角度函数的局部最大值。这些点是平移和旋转不变的。而且，它们在不同的照明条件下是稳定的。在对不同兴趣点检测器[214,215]的比较研究中，Harris角被证明是最可重复且最具信息性的。另外，它们可以非常精确：子像素精度可以通过局部最大值附近的角度函数的二次近似来实现。

3.2.1讨论
图3.2显示了使用此度量检测到的两个通过旋转相关的示例图像的角点。请注意，找到的特征对应于图像中显示强度图案中的二维变化的位置。这些可能对应于真正的“角点”，但探测器也可以在其他结构上，例如T形接头，高曲率点等。这同样适用于本章所述的所有其他角点探测器。当需要真正的角点时，基于模型的方法肯定更合适。

图3.2旋转图像示例中检测到的Harris角。

从图中可以看出，在旋转版本（右图）中也发现了许多但并非所有在原始图像中检测到的特征（左）。换句话说，Harris检测器在旋转下的可重复性很高。另外，通常在提供信息的位置处发现特征，即，强度模式具有高度可变性。这使得它们更具有辨别力，更容易引入通信。

3.3 SUSAN探测器
SUSAN角点探测器由Smith和Brady [232]引入，并依赖于一种不同的技术。不是评估可能对噪声敏感且计算上更昂贵的局部梯度，而是使用形态学方法。
SUSAN代表最小的Univalue Segment Assimilating Nucleus，是一种通用的低级图像处理技术，除角点检测外，还用于边缘检测和噪声抑制。基本原理如下（另见图3.3）。对于图像中的每个像素，我们考虑围绕它的固定半径的圆形邻域。中心像素称为核，其强度值用作参考。然后，该圆形邻域内的所有其他像素被划分为两类，这取决于它们是否具有与核相似的“相似”强度值或“不同”强度值。通过这种方式，每个图像点都与其相关联，具有相似亮度的局部区域（铸造的usan），其相对大小包含关于该点处图像结构的重要信息（也见图3.3）。在图像的或多或少的均匀部分中，具有相似亮度的局部区域几乎覆盖整个圆形邻域。在近边缘处，该比率下降至50％，并且在拐角附近它进一步降低至约25％。因此，可以将角检测为图像中的位置，其中在局部邻域中具有相似强度值的像素的数量达到局部最小值并且低于预定阈值。为了使该方法更稳健，与核更接近的像素接收更高的权重。此外，一组规则用于抑制定性“坏”特征。然后从剩余的候选者中选择SUSAN（最小的用户）的局部最小值。检测到的SUSAN角的示例如图3.4所示。

图3.3通过将圆形邻域分成“相似”（橙色）和“不相似”（蓝色）区域来检测SUSAN角。角点位于“相似”区域（usan）的相对面积达到低于特定阈值的局部最小值的位置。

图3.4为示例图像找到的SUSAN角。

3.3.1讨论
所发现的特征显示出这种（人工旋转的）图像的高重复性。但是，许多特征都位于边缘结构上而不是角点上。对于这些点，定位对噪声敏感。而且，基于边缘的点也不太具有辨别力。

到目前为止描述的两个检测器仅在平移和旋转下是不变的。这意味着仅当图像通过平移和/或旋转相关时才在相应位置处检测角。在接下来的部分中，我们将描述具有更高水平的视点不变性的探测器，它可以承受尺度变化甚至变形。除了在变换图像之间更好地匹配之外，这些还具有在一系列尺度或形状上检测特征的优点。
或者，可以通过使用多尺度方法获得该效果。在这种情况下，不是尺度不变的检测器以不同的比例（即，在平滑和采样之后）被施加到输入图像。

3.4 Harris-Laplace / A ffine
Mikolajczyk和Schmid开发了一种尺度不变的角点探测器，称为Harris-Laplace，以及一种不变的角点探测器，被称为Harris-A ffine [143]。

3.4.1哈里斯 - 拉普拉斯
Harris-Laplace以多尺度Harris角点检测器作为初始化来确定局部特征的位置。然后根据Lindeberg等人提出的比例选择确定特征尺度。 [116,120]。我们的想法是选择局部结构的特征尺度，给定的函数在尺度上达到极值（见图3.5）。所选择的比例在定量意义上是特征性的，因为它测量特征检测算子和局部图像结构之间存在最大相似性的比例。因此，区域的大小与每个点的图像分辨率无关地选择。正如Harris-Laplace所说，拉普拉斯算子用于比例选择。这已被证明在[141]和[38]的实验比较中给出了最好的结果。这些结果可以通过拉普拉斯核的圆形来解释，当其尺度适应于局部图像结构的尺度时，其作为匹配滤波器[58]。

图3.5特征尺度示例。顶行显示使用不同缩放拍摄的图像。底行显示拉普拉斯算子对两个对应点的比例的响应。左图像和右图像的特征尺度分别为10.1和3.9。比例的比率对应于两个图像之间的比例因子（2.5）。顶行中显示区域的半径等于所选比例的3倍。

图3.6显示了通过应用Harris-Laplace检测器获得的尺度不变的局部特征，用于通过尺度变化相关的同一场景的两个图像。为了不使图像过载，仅显示在两个图像中检测到的一些相应区域。类似的选择机制已用于本调查中显示的所有后续图像对。

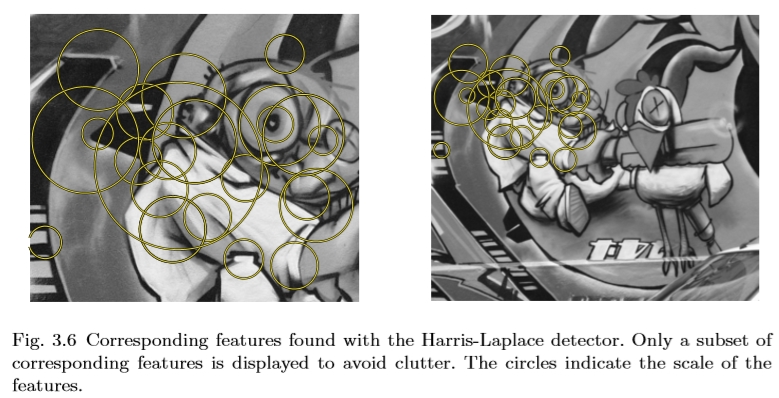
图3.6 Harris-Laplace探测器的相应特征。仅显示相应特征的子集以避免混乱。圆圈表示特征的比例。

3.4.2 Harris-Affine
给定一组基于哈里斯 - 拉普拉斯检测方案在其特征尺度上提取的初始点，如Lindeberg等人提出的椭圆形区域的迭代估计。 [118,121]允许获得一个不变的角点。这些是椭圆形，而不是圆形区域。该程序包括以下步骤：
（1）用Harris-Laplace检测器检测初始区域。
（2）用第二矩矩阵估计一个ffine形状。
（3）将ffine区域标准化为圆形区域。
（4）重新检测标准化图像中的新位置和比例。
（5）如果新点的第二矩矩阵的特征值不相等，则转到步骤2。
迭代如图3.7所示。

图3.7在存在ffine变换（顶部和底部行）的情况下迭代检测一个不变的兴趣点。第一列显示用于初始化的点。连续列显示迭代1,2,3和4之后的点和区域。注意，区域在4次迭代后会聚到相应的图像区域。

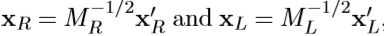第二矩矩阵的特征值（见等式（3.3））用于测量点邻域的形状。更确切地说，我们确定将点邻域的强度模式投影到具有相等特征值的强度模式的变换。该变换由第二矩矩阵的平方根给出。可以证明，如果两个点xR和xL的邻域通过变换相关，则它们的归一化版本通过简单相关旋转 [13,121]。该过程如图3.8所示。在归一化帧中计算的矩阵ML和MR也是旋转矩阵。注意，旋转保持图像块的特征值比，因此，可以仅确定旋转因子的变形。

图3.8说明使用第二矩矩阵进行归一化的图。用矩阵变换图像坐标。

假定第二矩矩阵的行列式大于零并且信噪比足够大，则可以将ffine形状的估计应用于任何初始点。因此，我们可以使用这种技术来估计Harris-Laplace探测器提供的初始区域的形状。

Harris-A ffine探测器在同一场景的两幅图像上的输出如图3.9所示。除了比例之外，区域的形状现在也适合于下面的强度图案，以便尽管由视点改变引起的变形确保覆盖物体表面的相同部分。

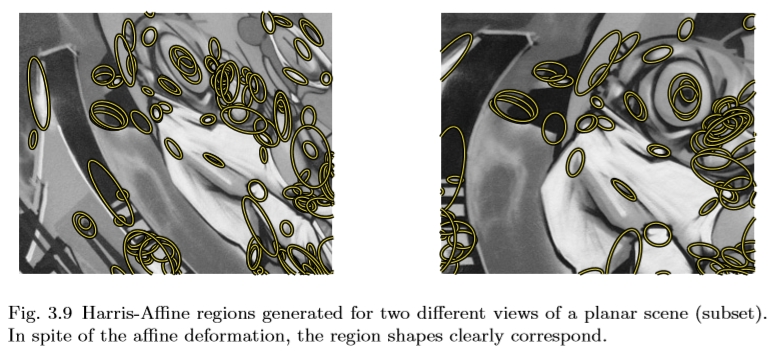
图3.9为平面场景（子集）的两个不同视图生成的Harris-A ffine区域。尽管有变形，但区域形状明显对应。

3.5基于边缘的区域
获得ffine不变性的更具启发性的技术是利用通常可以在Harris角点附近找到的边缘的几何形状。 Tuytelaars和Van Gool [247,249]提出了这种方法。这种方法背后的基本原理是边缘通常是相当稳定的图像特征，可以在一系列视点，比例和照明变化中检测到。此外，通过利用边缘几何形状，问题的维度可以显著降低。实际上，如下所示，通过利用附近的边缘几何形状，可以将所有可能的函数（或4D，一旦中心点固定）的6D搜索问题简化为一维问题。在实践中，我们从Harris角点p（参见第3.2节）[84]和附近边缘开始，用Canny边缘检测器[29]提取。为了提高尺度变化的稳健性，这些基本特征在多个尺度上提取。两个点p1和p2沿着边缘沿两个方向远离拐角，如图3.10所示。它们的相对速度通过相对不变的参数l1和l2的相等性来耦合：

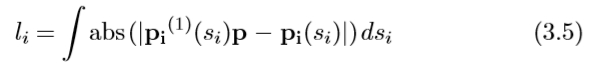
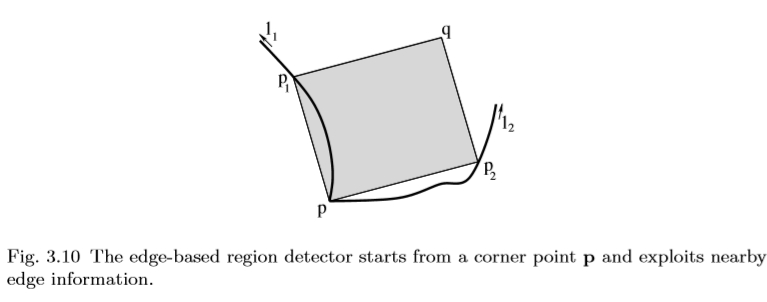
图3.10基于边缘的区域检测器从角点p开始并利用附近的边缘信息。

使用si任意曲线参数（在两个方向上，i = 1,2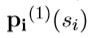），相对于si的绝对导数，abs（）绝对值和| ...决定因素。该条件规定接头（p，p1）和边缘之间以及接头（p，p2）和边缘之间的区域保持相同。从现在开始，我们只是在引用l1 = l2时使用l。
对于每个值l，两个点p1（l）和p2（l）连同角点p define平行四边形Ω（l）：由矢量和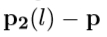跨越的平行四边形（见图3.10）。这产生了作为l的函数的一维平行四边形区域。从该1D族中选择一个（或几个）平行四边形，其中以下光度量的纹理通过极值。

图3.11最初检测到的基于边缘的区域（子集）的区域形状。

为n阶，（p + q）th度矩在区域Ω（l）上计算，pg为该区域的重心，用强度 I（x，y）加权，q为平行四边形的角与角点p相反（见图3.10）。添加了这些公式中的第二个因子，以确保在强度组合下的不变性。
对于直边，沿整个边缘 l = 0。在这种情况下，组合公式（3.7）中给出的两个光度量，并且两个函数达到最小值的位置被用来确定参数s1和s2。而且，不是依赖于Harris角点检测，而是可以使用直线交点。检测到的区域示例如图3.11所示。

3.5.1从平行四边形到椭圆形

请注意，使用此方法找到的区域是平行四边形。这与许多其他不变的检测器（例如基于第二力矩矩的检测器）形成对比，输出形状是椭圆形。为了比较的均匀性和便利性，有时将这些平行四边形区域转换成椭圆形是有利的。这可以通过选择具有与最初检测到的区域相同的十二阶矩的椭圆来实现，这是一种非常协变的构造方法。使用此过程生成的椭圆区域如图3.12所示。请注意，在此转换过程中会丢失一些信息，因为椭圆具有旋转自由度，这是在原始表示中固定的。

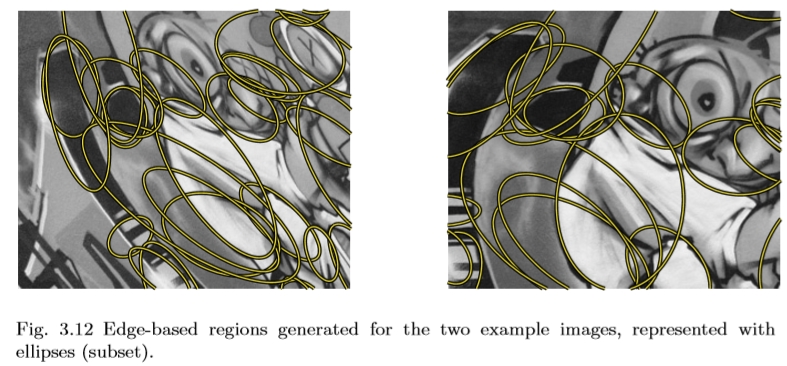
图3.12为两个示例图像生成的基于边缘的区域，用省略号（子集）表示。

3.6讨论
本章描述了几种角点检测方法。如前所述，基于角点的特征不一定对应于3D世界中的真实角点。实际上，目标是提取稳定的特征，即使观察条件发生变化也能很好地匹配。
在许多独立评估中，Harris探测器被认为是最稳定的探测器[83,138,215]。这种方法还有多尺度和规模以及不变的不变扩展。它是提供大量特征的便捷工具。或者，可以使用SUSAN检测器。它更有效但对噪声更敏感。第6.3节描述了使用机器学习技术的优化SUSAN检测器。如2.2和2.3节中所讨论的，基于轮廓的角点检测器适用于线描图像，但在自然界中基于强度的方法基本上更稳定。

重要的是要注意，在局部平面区域的情况下，并且假设相机距离物体相对较远，该变换模型仅适用于视点变化。然而，通常在物体边界附近发现拐角，因为这是通常发生强度变化的地方。因此，区域提取过程通常基于对非平面结构的测量，例如包括对象的背景或另一个面。在这些情况下，视点不变性将受到限制，并且对背景变化的鲁棒性也会受到影响。 [251]的工作表明了一种可能的出路。搜索像EBR这样的区域边界的探测器受这种现象的影响较小。然后可以通过检测到的轮廓界定测量区域，从而在许多实际情况中排除非平面部分。

从积极的方面来说，与其他类型的特征相比，角点通常更好地定位在图像平面中。该定位精度对于某些应用是重要的，例如，用于相机校准或3D重建。然而，它们的尺度并没有得到很好的定义，因为角度结构在很大范围内变化很小。尺度选择仍然适用于Harris探测器的原因是特征点不是精确地定位在角点边缘而是略微位于角点内部结构体。

4斑点探测器

在角点之后，第二个最直观的局部特征是blob。正如前一节中的情况一样，我们选择了一些在许多应用程序中证明成功的方法，并更详细地描述了这些方法。这些方法通常为前一章讨论的方法提供补充特征。我们从基于衍生的方法开始：Hessian检测器（第4.1节）。接下来，我们考虑这种方法的尺度不变和ffine不变扩展，创造了Hessian-Laplace和Hessian-A ffine（第4.2节）。最后，我们描述了显著区域探测器，它基于强度概率分布的熵（第4.3节）。我们以简短的讨论结束本章。

4.1 Hessian探测器
从图像强度函数I（x）的泰勒展开发出的第二个2×2矩阵是Hessian矩阵：

与 Ixx 等二阶高斯平滑图像导数。这些通过描述等值面的法线如何变化来编码形状信息。因此，它们捕获局部图像结构的重要属性。特别有趣的是基于行列式的过滤器和该矩阵的轨迹。后者通常被称为拉普拉斯算子。两种测量的局部最大值可用于检测图像中的斑点状结构[16]。

拉普拉斯算子是一个可分离的线性滤波器，可以用高斯差分滤波器（DoG）滤波器近似得到。拉普拉斯滤波器在斑点提取的背景下有一个主要缺点。通常在轮廓或直边附近发现局部最大值，其中信号变化仅在一个方向上[138]。这些最大值不太稳定，因为它们的定位对噪声或相邻纹理的微小变化更敏感。在发现用于恢复图像变换的对应关系的背景下，这主要是一个问题。解决这个问题的一种更复杂的方法是选择一个位置和尺度，其中Hessian矩阵的轨迹和行列式同时呈现局部极值。
这产生了点，对于这些点，二阶导数检测两个正交方向上的信号变化。在Harris探测器中探索了类似的想法，尽管只有一阶导数。
基于Hessian矩阵的特征检测过程如图4.1所示。给定原始图像（左上），首先计算二阶高斯平滑图像导数（下部），然后将其组合成Hessian的行列式（右上）。

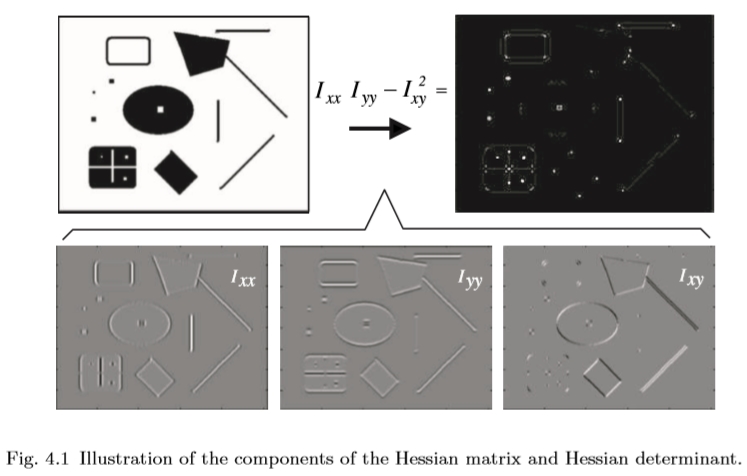
图4.1 Hessian矩阵和Hessian行列式的分量图。

图4.2显示了使用Hessian行列式检测到的示例图像对的兴趣点。二阶导数是对称滤波器，因此它们在信号变化最显著的点上给出了微弱的响应。因此，最大值定位在脊和斑点处，其中高斯核σD的大小与斑点结构的大小匹配。

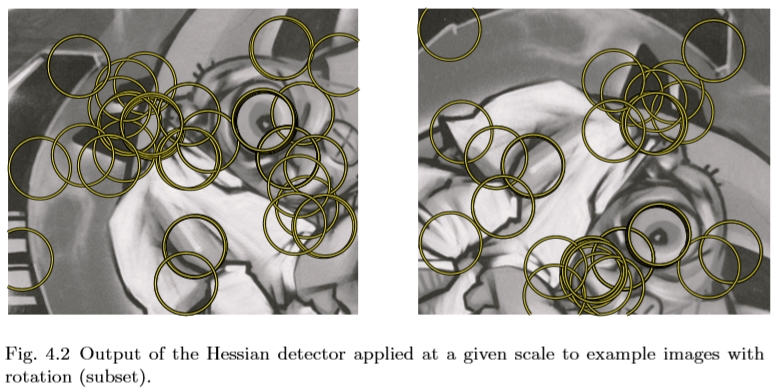
图4.2以给定比例应用的Hessian检测器输出到具有旋转（子集）的示例图像。

4.2 Hessian-Laplace / Affine
Hessian-Laplace和Hessian-Affine探测器在精神上与他们基于Harris的对手Harris-Laplace和Harris-A ffine相似，

Hessian-Laplace和Hessian-A ffine探测器在精神上类似于他们的基于Harris的对应物Harris-Laplace和Harris-A ffine，在3.4节中描述，除了它们从Hessian的决定因素而不是Harris角点开始。这将方法转换为视点不变的斑点检测器。它们也是由Mikolajczyk和Schmid [143]提出的，并且是对他们基于Harris的对应物的补充，因为它们对图像中的不同类型的特征作出反应。图4.3和4.4分别显示了尺度不变的Hessian-Laplace和一个不变的Hessian-A ffine的检测结果的一个例子。

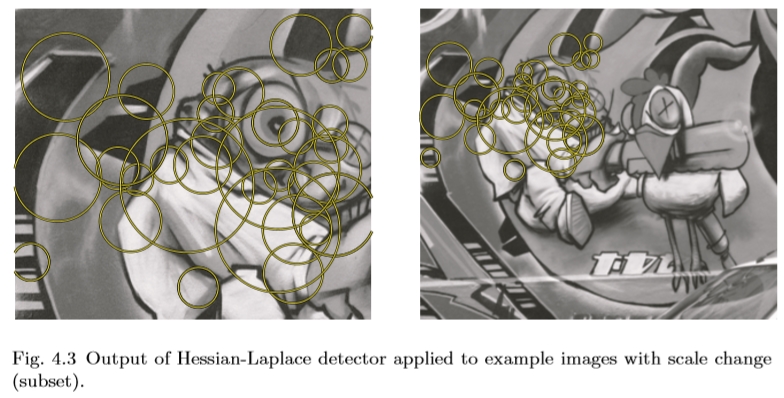
图4.3应用于具有尺度变化（子集）的示例图像的Hessian-Laplace检测器的输出。

图4.4为示例场景（子集）的两个视图生成的Hessian-Affine区域。

与基于Harris的探测器一样，使用Hessian-Laplace探测器找到的区域数量可以通过对Hessian行列式以及拉普拉斯响应进行阈值处理来控制。通常，可以提取大量特征，从而实现图像的良好覆盖，这是基于Hessian的检测器的优点之一。
此外，该探测器还能以细微的比例响应一些角点结构（见图4.1）。然而，返回的位置比Harris点更适合于尺度估计，这是因为基于二阶高斯导数使用类似的空间和尺度定位滤波器。

这项工作的可能扩展之一是探索Hessian矩阵，以使用由该矩阵的特征值编码的其他形状信息。

4.3突出区域

Kadir和Brady [98]提出的显著区域检测器不是建立在图像中的衍生信息上，而是受信息理论的启发。这个特征检测器背后的基本思想是寻找显著特征，其中显著性被定义为局部复杂性或不可预测性。它通过局部图像区域内的强度值的概率分布函数的熵来测量。然而，仅仅考虑熵并不能准确地定位尺度上的特征，因此作为附加标准，特征的尺度空间中的自相异性被添加为额外的加权函数，有利于良好定位的复杂特征。检测以两个步骤进行：首先，在每个像素x处，在一定范围的标度s上评估概率分布p（I）的熵H.

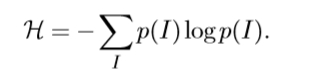
基于围绕x的半径s的圆形邻域中的强度分布，经验地估计概率分布p（I）。记录熵的局部最大值。这些是候选显著区域。其次，对于每个候选显著区域，p（I）相对于标度s的导数的大小被计算为

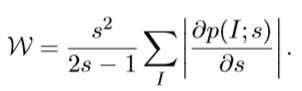
然后将显著性Y计算为

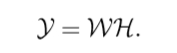
整个图像上的候选显著区域按其显著性Y排序，并保留排名前P的区域。还提出了一种不变的检测器版本，其中同时寻找尺度s上的局部最大值和形状参数（取向θ和椭圆区域的主轴与短轴λ的比率）。但是，这严重减慢了计算速度。使用ffine不变版本的检测区域示例如图4.5所示。关于这种方法的更多细节可以在[99]中找到。

图4.5为两个示例图像找到的与视点（子集）变化相关的显著区域。

4.3.1讨论
由于加权因子测量了比例尺上的自相异性，因此探测器通常依赖于图像中的斑点状结构。这就是为什么我们将该方法编目为blob检测器的原因。但请注意，与其他斑点探测器相比，斑点的对比度对检测没有任何影响。
使用此方法找到的特征数量通常相对较低。与许多其他检测器不同，由于基于熵的标准，所提取的特征的排名是有意义的，其中从最顶部的标准是最稳定的。该属性已经在类别级对象识别的背景下进行了探索，特别是与分类器结合，其中复杂性在很大程度上取决于特征的数量（例如，[65]）。

4.4讨论

Blob检测器已广泛应用于不同的应用领域。除了上述方法之外，DoG（高斯的差异）[124]和SURF（加速的鲁棒特征）[15]也可以编目为斑点检测器。然而，由于他们的提取过程都集中在效率上，我们将他们的讨论推迟到第6节。
第5节中描述的一些方法也与blob检测器具有共同的特征。特别是IBR（基于强度的区域）[248]和MSER（最大稳定的极值区域）[134]经常在图像中找到斑点状结构。然而，除了类似blob的结构外，它们还可以检测到其他更不规则形状的图案，我们认为这些图案具有独特的性质。

Blob探测器在某种意义上与角探测器互补。因此，它们经常一起使用。通过使用多个互补特征检测器，可以更好地覆盖图像，并且性能变得更少地依赖于实际图像内容。这已经被利用，例如在[110,140,231]中。
通常，类似斑点的结构往往不像角点那样精确地定位在图像平面中，尽管它们的比例和形状比角点更好地定义。角点的位置可以由单个点识别，而斑点只能通过其边界来定位，这些边界通常是不规则的。另一方面，角点的比例估计是不明确的，例如边缘的交叉点存在于宽范围的尺度上。然而，斑点的边界，即使是不规则的，也可以很好地估计斑块的大小，从而得到斑块的规模。这使得它们不太适合于例如相机校准或3D重建。另一方面，对于物体识别，通常不需要精确的图像定位，因为整个识别过程非常嘈杂。然而，诸如SIFT [124]的鲁棒描述符可以匹配这些特征。匹配blob的比例允许然后假设对象的大小[140]，这使得它们在识别应用中非常有用。
最后，使用上述方法检测到的特征数量差别很大。在图像中通常只有几十个显著区域，而Hessian-Laplace或Hessian-A方法允许提取多达数百或数千个特征。根据所使用的应用和算法，任何一种情况都是有利的。有关此问题的进一步讨论，请参阅第7节。

5 区域探测器

在本章中，我们讨论了许多直接或间接涉及图像区域提取的特征检测器。首先，我们描述基于强度的区域（第5.1节），然后是最大稳定的极值区域（第5.2节）。最后，我们讨论超像素（第5.3节）。这些区域由不同的方法提供，但侧重于相似的图像结构并具有相似的属性。传统上，超像素不被视为局部特征，并且对于观看条件的变化具有有限的鲁棒性，但是它们目前越来越多地用于图像识别的背景中。因此，我们将所有上述特征包含在同一类别中。

5.1基于强度的区域
在这里，我们描述了Tuytelaars和Van Gool [248,249]提出的检测不变区域的方法。它从强度极值（在多个尺度上检测）开始，以径向方式探索它们周围的图像，描绘任意形状的区域，然后用椭圆代替。

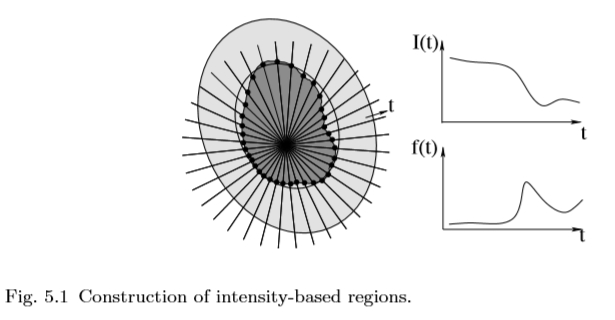
图5.1基于强度的区域的构建。

更确切地说，给定局部极值强度，研究从极值发出的光线的强度函数（见图5.1）。沿每条光线评估以下函数：

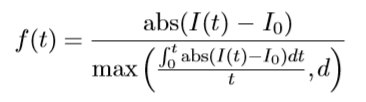
沿着光线的任意参数，I（t）是位置t处的强度，I0 是极值处的强度值，d 是为了防止被零除以而添加的小数字。该函数达到极值的点在几何和线性光度变换（给定光线）下是不变的。通常，在强度突然增加或减少的位置达到最大值。函数 f（t）本身已经是不变的。然而，选择点，此函数达到极值以进行稳健选择。接下来，对应于来自相同局部极值的射线的 f（t）的最大值的所有点被链接以包围一个不变的区域。这种通常不规则形状的区域被具有相同形状的椭圆取代，直到二阶。这种椭圆形装置是一种灵活的协变结构。使用此方法检测到的区域示例如图5.2所示。

图5.2为graffiti图像（子集）找到的基于强度的区域。

5.2极其稳定的极值区域
Matas等人提出了MSER或最大稳定极值区域。 [134]。最大稳定极值区域是适当阈值化图像的连通分量。 “极值”一词指的是MSER内的所有像素具有比其外边界上的所有像素更高（明亮的极值区域）或更低（暗极值区域）强度的特性。 MSER中的“最大稳定”描述了在阈值选择过程中优化的属性。

该组极值区域E，即通过阈值处理获得的所有连通分量的集合，具有许多所需的特性。首先，图像强度的单调变化使E保持不变。其次，连续几何变换保留了拓扑 - 来自单个连通分量的像素被转换为单个连通分量。最后，没有比图像中的像素更多的极值区域。因此，定义了一组区域，这些区域在广泛的几何和光度变化下保留，并且具有与例如在窄基线匹配中常用的固定大小的方形窗口组相同的基数。
该组极值区域E的枚举非常有效，在图像像素的数量上几乎是线性的。枚举如下进行。首先，像素按强度排序。排序后，像素在图像中标记（按递减或递增顺序），并使用联合算法[219]维护生长和合并连接组件及其区域的列表。在枚举过程中，存储作为强度函数的每个连通分量的面积。在极值区域中，“最大稳定”区域是对应于阈值的阈值，对于该阈值，作为阈值的相对变化的函数的相对面积变化处于局部最小值。换句话说，MSER是图像的一部分，其中局部二值化在大范围的阈值上是稳定的。基于相对面积变化的MSER稳定性的定义对于变换（光度和几何）都是不变的。

MSER的检测与阈值处理有关，因为每个极值区域是阈值图像的连通分量。然而，没有寻求全局或“最佳”阈值，测试所有阈值并评估连接组件的稳定性。 MSER检测器的输出不是二值化图像。对于图像的某些部分，存在多个稳定阈值，并且在这种情况下输出嵌套子集的系统。
对于许多ffine不变检测器，输出形状是椭圆形。但是，对MSER来说并非如此。检测到的原始区域的例子如图5.3所示。使用与上述IBR相同的程序，可以基于第一和第二形状矩来设置椭圆。这导致一组特征，如图5.4所示。或者，可以根据沿区域轮廓[135]的一组稳定点来定义局部框架。这提供了另一种方案来使区域针对变形进行归一化。

图5.3使用MSER在gra ffi ti图像（子集）上检测到的区域。

图5.4 graffiti图像的最终MSER区域（子集）。

5.2.1讨论

MSER特征通常锚定在区域边界上，因此与其他斑点检测器相比，所得区域被精确定位。该方法最适用于可以很好地分割的结构化图像 - 理想情况下，具有由强烈强度变化分隔的均匀区域的图像。在缺点方面，它被发现对图像模糊敏感[145]，这可以通过图像模糊破坏稳定性标准的事实来解释。该问题最近在[177]中得到了解决。该方法也相对较快。它是目前ffine不变特征探测器中最有效的。它主要用于识别或匹配特定对象（例如，[166,231]），并且表现出较低的对象类识别性能[139]。

5.3基于分段的方法（超像素）
上述两种方法提取了小区域，其强度模式相对于其周围环境明显突出。这让人联想到传统的图像分割技术。然而，图像片段通常相对较大 - 实际上太大，不能用作局部特征。通过增加段的数量，可以获得新的图像表示，其中图像段通常在大多数基于局部特征的应用程序中所需的位置和区别之间具有正确的交易（参见图5.5）。 Mori等人提倡将这种低级像素分组为原子区域。 [159]和Ren和Malik [184]，他们将得到的原子区域称为超像素。该术语指的是超像素可以被认为是原始图像像素的更自然且在感知上更有意义的替代。

图5.5为示例图像生成的超像素。

在[159,184]中，使用标准化切割从图像中提取超像素[227]，但是这里可以使用任何数据驱动的分割方法。基于归一化切割的方法是经典的图像分割算法，其利用成对亮度，颜色或纹理之间的像素的效率。为了强制执行局部性，在构造效率矩阵时仅考虑局部连接。超像素的一个例子如图5.5所示。
与传统的局部特征相比，通过构造超像素覆盖整个图像并且不重叠。除了小的轮廓细节和不可见的轮廓之外，还可以使用多个分割来增加对象边界与相邻超像素之间的边界重合的可能性。从图像中提取的所有超像素具有相似的比例，因此该方法不是尺度不变的。已经提出了一种基于约束Delauney三角剖分的替代构造方法来获得抗尺度变化的鲁棒性[183]。
这些特征不太适合于匹配或物体识别，因为这些区域是均匀的，因此不具有区别性，并且边界提取的可重复性低。它们已经成功地用于建模和利用中级视觉线索，例如曲线连续性，区域分组或用于语义图像分割的图形/地面组织。

5.4讨论
用上述方法检测的局部特征通常代表均匀区域。虽然这对于检测步骤是可接受的，但是可能对后面的描述和匹配产生问题。实际上，同质区域缺乏独特性。幸运的是，通过增加测量区域可以很容易地克服这个问题。换句话说，我们使用更大比例的区域来计算描述符，使得它还包含周围图像结构的一部分并捕获区域边界的形状。这通常有助于增加辨别力并匹配图像之间的区域。
基于强度的区域和最大稳定的极值区域通常提供非常相似的特征。因此，这些方法不是互补的。当该区域是非凸的时，IBR可能会分解，但是对于区域轮廓中的小间隙，它更稳健。另一方面，MSER已被证明对[145]中的图像模糊相对敏感，因为这直接影响稳定性标准。最近在[177]中解决了这个问题。然而，除了图像模糊的情况之外，MSER在[145]中的可重复性方面得分最高。
如前所述，区域探测器通常会探测到类似blob的结构 - 尽管它们并不局限于这种类型的区域。结果，它们与斑点相比较不那么互补。
基于区域的检测器通常在其定位方面非常准确。它们特别适用于具有结构良好的场景的图像，清晰描绘的区域，例如包含具有印刷表面的对象的图像，建筑物等。

尽管超像素与其他区域检测器具有某些特征，但它们并不相同。它们不重叠，覆盖整个图像。它们的可重复性来自分割方法的弱稳健性。最重要的是，它们是在不同的背景下开发的，其目的是通过仅关注超像素而不是分析所有像素来加速图像分析。因此，超像素被认为是像素的更大等价物，可以通过单个强度或颜色值来描述第一近似值。这与局部特征形成对比，局部特征应该是独特的，并且在理想情况下，是唯一可识别的。然而，使用区域边界来构建独特的描述符可以克服传统兴趣点所带来的遮挡问题[68]。

6 高效的实施

到目前为止所描述的大多数特征检测器涉及衍生物的计算或更复杂的测量，例如Harris检测器的第二矩矩阵或凸区检测器的熵。由于需要对包括位置，比例和形状的特征坐标空间中的每个位置重复该步骤，这使得特征提取过程计算上昂贵，因此不适合于许多应用。
在本节中，我们描述了几个以计算效率开发的特征检测器作为主要目标之一。 DoGs探测器使用多个尺度空间金字塔近似拉普拉斯算子（参见第6.1节）。 SURF利用积分图像来有效地计算Hessian矩阵的粗略近似（第6.2节）。 FAST仅使用决策树评估有限数量的单个像素强度（参见第6.3节）。

6.1高斯的差异

在[47,76,81,124,126]中已经提出了高斯差分检测器（简称DoG）。它是一个尺度不变的探测器，通过近似拉普拉斯L2xx + L2yy来提取图像中的斑点（另见4.1节）。基于尺度空间理论[117,234,258]中的差分方程，可以证明拉普拉斯算子对应于尺度方向上图像的导数。由于给定方向上相邻点之间的差异近似于该方向上的导数，因此不同尺度的图像之间的差异近似于相对于比例的导数。此外，高斯模糊通常用于生成各种尺度的图像。因此，DoG图像产生接近LoG的响应。然后避免在x和y方向上计算二阶导数，如图6.1所示。

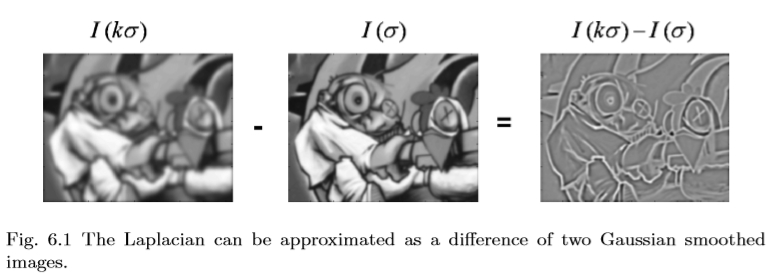
图6.1拉普拉斯算子可以近似为两个高斯平滑图像的差异。

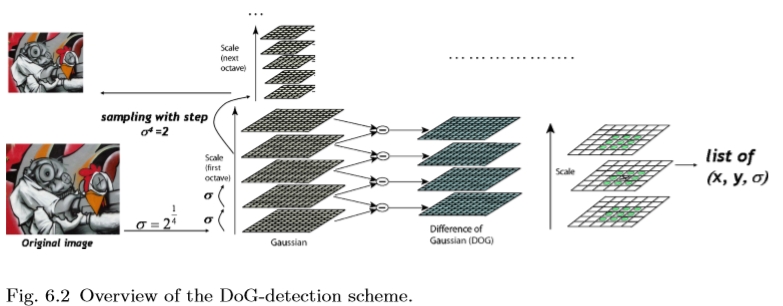
图6.2 DoG检测方案概述。

实际的计算方案如图6.2所示。使用高斯卷积掩模对图像进行几次平滑处理。这些平滑的版本成对组合以计算一组DoG blob响应图。这些地图中的局部最大值位于空间和具有非最大抑制的尺度上，并且位置进一步通过二次插值来确定。在几个平滑步骤之后，可以对图像进行二次采样以处理下一个八度音阶。
由于拉普拉斯算子对边缘给出强响应，因此增加了额外的滤波步骤，其中计算完整的Hessian矩阵的特征值并评估它们的强度。这个过滤步骤不会对整个处理时间造成太大影响，因为只需要有限数量的图像位置和比例。在我们的示例图像中检测到的DoG特征如图6.3所示。使用此方法可以处理每秒几帧。

图6.3使用DoG检测器检测到的局部特征。

6.2 SURF：加快了强大的特征
在实时人脸检测的背景下，Viola和Jones提出使用积分图像[252]，它允许非常快速地计算Haar小波或任何盒式卷积滤波器。首先，我们将描述积分图像的基本概念。然后我们展示了如何使用这种技术来获得Hessian矩阵的快速近似，如SURF（Speeded-Up Robust Features）[15]中所使用的那样。

6.2.1积分图像

在位置 x =（x，y）处输入积分图像 IΣ（x）表示由原点和x形成的矩形区域的输入图像I中的所有像素的总和。

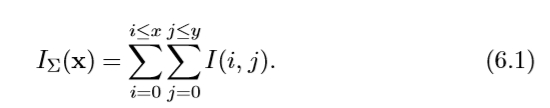
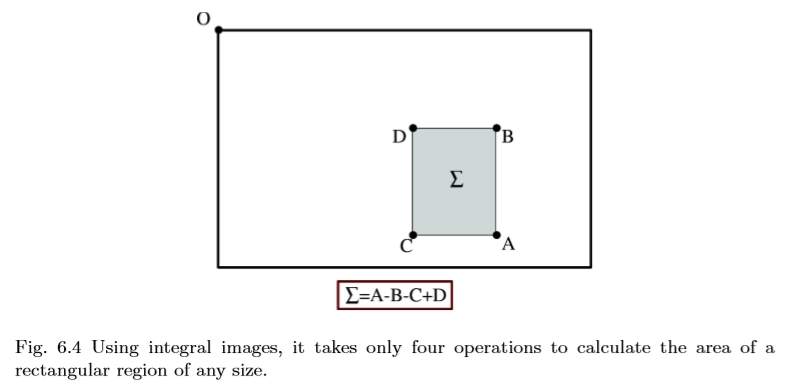
图6.4使用积分图像，只需四个操作即可计算出任意大小矩形区域的面积。

一旦计算出积分图像，就需要四次加法来计算任何直立矩形区域的强度之和，如图6.4所示。而且，计算时间与矩形区域的大小无关。

6.2.2 SURF
Bay等人提出了SURF或加速鲁棒特征。 [15,14]。它是基于Hessian矩阵的尺度不变特征检测器，例如Hessian-Laplace检测器（参见4.2节）。然而，不是使用不同的度量来选择位置和比例，而是使用Hessian的行列式。 Hessian矩阵大致近似，使用一组boxtype滤波器，并且当从一个刻度到下一个刻度时不应用平滑。

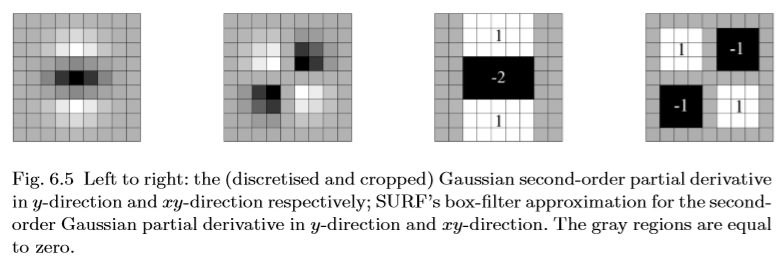
图6.5从左到右：分别在y方向和xy方向上的（离散和裁剪的）高斯二阶偏导数; SURF的盒式滤波器近似于y方向和xy方向上的二阶高斯偏导数。灰色区域等于零。

高斯分布是尺度空间分析的最佳选择[7,67,106,117]，但在实践中它们必须离散化（图6.5左），这会引入伪像，特别是在小高斯核中。 SURF使用如图6.5右半部分所示的盒式滤波器进一步推动近似。这些近似的二阶高斯导数，可以使用积分图像非常快速地进行评估，与其大小无关。令人惊讶的是，尽管有粗略的近似，特征检测器的性能与离散高斯的结果相当。 Box滤波器可以产生高斯导数的足够近似，因为处理链中存在许多其他重要噪声源。

图6.5中的9×9盒滤波器是具有σ= 1.2的高斯的近似值，并且表示嵌套比例（即，最高空间分辨率）。我们将用Dxx，Dyy和Dxy表示它们。应用于矩形区域的权重对于计算效率而言保持简单，但是我们需要进一步平衡Hessian行列式的表达式中的相对权重与最小尺度的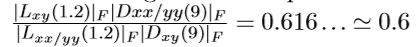

，其中 | x | F是Frobenius范数。这产生了

Hessian的近似行列式表示位置x处的图像中的斑点响应。这些响应存储在blob响应图中，并且使用二次插值检测并重新定义局部最大值，与DoG一样（参见第6.1节）。图6.6显示了我们的示例图像的SURF检测器的结果。据报道，SURF比DoG快五倍。

6.3快速：加速段测试的特征

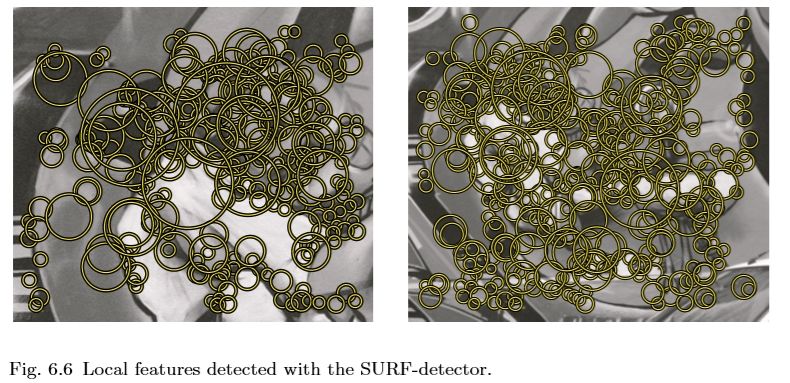
图6.6使用SURF检测器检测到的局部特征。

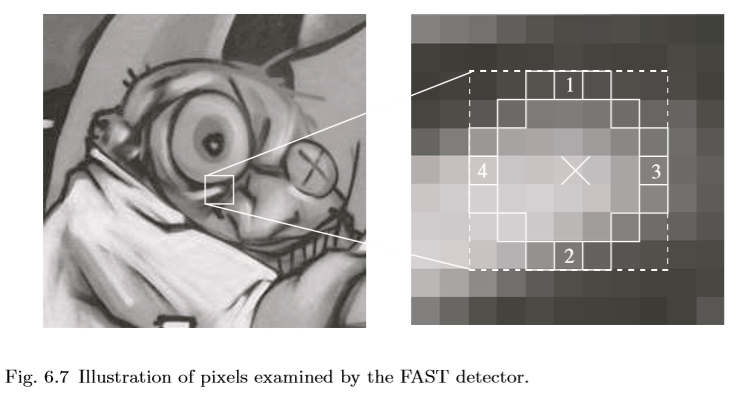
图6.7 FAST检测器检查的像素图示。

图6.8使用FAST检测器检测到的局部特征。

由Rosten和Drummond在[202,203]中介绍的FAST探测器建立在先前在3.3节中讨论过的SUSAN探测器[232]上。 SUSAN计算邻域内像素的分数，其强度与中心像素相似。 FAST进一步采用了这一想法，FAST仅对点周围的固定半径圆进行比较。测试标准通过考虑角点候选者周围的16个像素的圆圈来操作（见图6.7）。最初，将像素1和2与阈值进行比较，然后将3和4以及最后的剩余部分进行比较。像素被分类为暗，相似和更亮的子集。来自[178]的ID3算法用于选择产生关于候选像素是否是拐角的最多信息的像素。这是通过基于该像素的正角和负角分类响应的熵来测量的。该过程在所有三个子集上递归应用，并在子集的熵为零时终止。然后将由此分区产生的决策树转换为C代码，创建一长串嵌套的if-then-else语句，将其编译并用作角点检测器。最后，非最大值抑制应用于圆中像素与中心像素之间的绝对差值之和。这样可以得到一个非常高效的探测器，其速度比第6.1节中讨论的DoG探测器快30倍 - 虽然对于尺度变化不是不变的。我们的示例图像中的FAST特征如图6.8所示。

在[112]中提出了利用拉普拉斯函数通过尺度选择对多尺度探测器的扩展。他们使用圆上像素和中心像素之间的灰度级差异来估计拉普拉斯算子，并仅保留此估计值最大的位置。这被证明足以产生大量的关键点候选者，在识别过程中不稳定的关键点候选者将被过滤掉。

6.4讨论

专注于效率的方法的最终目标通常是实时处理视频流或处理大量数据。但是，在某种程度上，这是一个不断变化的目标。计算能力随着时间的推移而迅速增加，但我们提取的特征数量或我们处理的数据库的大小也是如此。此外，特征检测不是最终目标，而只是处理链中的第一步，其次是匹配，跟踪，对象识别等。在许多应用中，仅通过增加训练样例的数量就可以获得显著的性能提升。因此，效率是对于在设计或选择特征检测器时应考虑的不变性或鲁棒性同等重要的主要特性之一。

回到第一点，特别是强大的图形处理单元的出现开辟了新的可能性。除了通过平台无关的算法变化获得加速的上述方法之外，通过利用可以用GPU实现的特殊结构和并行性，可以进一步加速。这些工作的一些例子可以在[89,230]中找到。在[28]和DoG检测器中讨论了基于FPGA的Harris-A特征检测器（见3.4节）的实现（参见[216]中的6.1节。这显著减少了计算正常情况下所有特征所需的时间）。大小的图像和视频帧速率处理。尽管有这种新的趋势，本节中描述的基本思想和方法仍然适用，因为它们非常通用且广泛适用。
最后，更有效的方法通常需要付出代价。必须在效率与另一方面的准确性或可重复性之间建立交换。令人惊讶的是，DoG，SURF和FAST探测器与标准的，计算量更大的特征探测器相比具有竞争力，并且可以为某些应用产生更好的结果。

7 讨论和结论

在我们调查的最后一部分中，我们概述了之前讨论过的方法，并突出了各自的优缺点。我们提供了一些关于如何使用这些特征的提示，以及如何为给定应用选择适当的特征检测器。最后，我们讨论一些未解决的问题和未来的研究方向。

7.1如何选择特征检测器？
下面，我们提供一些指南，说明用于特定应用的特征检测器。这并没有给出精确和明确的答案，但表明在搜索合适的探测器时需要考虑的几点。我们将读者引用到1.4节，其中我们定义了这里经常提到的局部特征的属性。
首先，我们根据它们提取的图像结构类型 - 角点，斑点或区域，在此调查中组织了特征检测器。根据图像内容，这些图像结构中的一些比其他图像结构更常见，因此对于不同的图像类别，给定检测器发现的特征的数量可能不同。如果事先对图像内容知之甚少，通常建议组合不同的互补检测器，即提取不同类型的特征。

其次，可以基于不变性水平来区分特征检测器。有许多评价关注这一属性[145,157,215]。人们可能总是试图选择可用的最高级别的不变性，以便尽可能多地补偿变化。然而，随着增加的不变性水平，特征的辨别力降低。由于要判断更多模式是等效的，因此需要估算更多参数，因此有更多可能的噪声源。此外，特征检测过程变得更加复杂，这既影响计算复杂性又影响可重复性。因此，一个基本的经验法则是不再使用手边应用程序真正需要的不变性。此外，如果预期的变换相对较小，通常最好依靠特征检测和描述的稳健性而不是增加不变性水平。这也是为什么特征检测器对透视变换不变的原因很少。

本调查中讨论的所有探测器对平移和旋转都是不变的。前者自动遵循使用局部特征。后者可以以有限的额外成本相对容易地实现。有时，不需要旋转不变性 - 例如，如果所有图像都是直立的并且物体也总是直立的（建筑物，汽车等）。在这些情况下，旋转不变检测器可以与旋转变量描述符组合，以确保良好的辨别力。在所有其他情况下，优选具有与检测器至多相同的不变性水平的描述符。
最后，要考虑的探测器有许多定性属性。根据应用场景，其中一些属性比其他属性更重要。在处理类别级别对象识别时，对小型外观变化的鲁棒性对于处理类内变异性非常重要。在为数据设置参数模型时，如相机校准或3D建模，定位精度至关重要。对于需要处理大量数据的在线应用程序或应用程序，效率是最重要的标准。

7.2探测器摘要

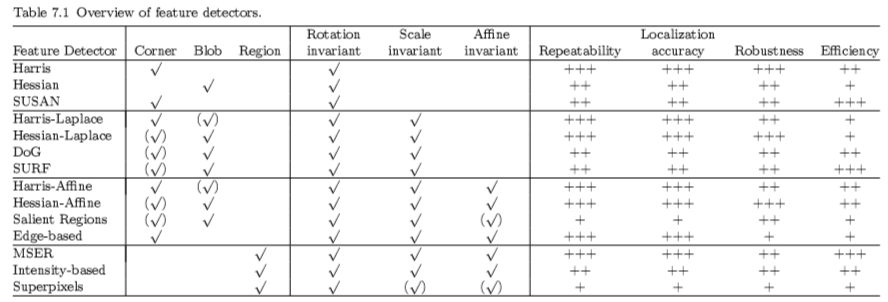
表7.1概述了第3-6节中描述的特征检测器的最重要属性。
表7.1中的特征检测器根据其不变性分为4组：旋转，相似性，效果和透视。我们比较每组中的属性。对于旋转不变特征，Harris检测器已经在许多测试中获得了最高的可重复性和定位精度。 Hessian探测器发现不太局部化的斑点，需要计算二阶导数。 SUSAN检测器避免了衍生物的计算，并且以其效率而闻名，但是没有平滑使得它更容易受到噪声的影响。所有旋转不变方法适用于仅使用特征的空间位置并且不期望大规模变化的应用，例如，来自运动或相机校准的结构。

在尺度不变组中，Harris-Laplace显示出从Harris检测器继承的高重复性和定位精度[215]。然而，由于角点的多尺度特性，其尺度估计不太准确。 Hessian-Laplace比单一尺度版本更强大[145]。这是因为类似斑点的结构在角度上比角点更好地定位，并且检测器从多尺度分析中受益，尽管它在图像平面中不太精确地定位。 DoG和SURF探测器的设计是为了提高效率，而其他特性则略有不同。但是，对于大多数应用来说，它们仍然不仅仅是足够的。在识别应用中，图像的数量和良好覆盖率是至关重要的，其中定位精度不太重要。因此，Hessian-Laplace探测器已成功用于各种分类任务，尽管存在具有更高重复率的探测器。随机和密集采样在这种情况下也提供了良好的结果，它确认了识别方法的覆盖要求[169] - 尽管它们导致的表示远不如兴趣点。 DoG检测器在匹配[26]和图像检索[124]方面表现非常出色，可能是由于空间定位和尺度估计精度之间的良好平衡。

请注意，对于刻度和ffine不变检测器，角点和斑点检测器之间的差异变得不那么直言不讳，大多数检测器检测到两种要素类型的混合 - 尽管它们仍然表现出对这两种类型的偏好。
一个不变的Harris和Hessian遵循先前小组的观察。显著区域需要为比例或空间中的每个区域候选计算直方图及其熵，这导致大的计算成本[145]。从积极的方面来看，可以根据区域的复杂性或信息内容对区域进行排名。一些应用程序利用它并且仅使用显著区域的一小部分，同时仍然在例如识别中获得良好性能[65]。最初，它们只是尺度不变的，但后来它们被扩展到了一个不变的不变性。基于边缘的区域聚焦在由边缘连接形成的拐角处，这提供了良好的定位精度和可重复性，但是检测到的特征的数量很小。

区域检测器基于分割均匀区域的边界的想法。基于强度的区域使用启发式方法并找到与MSER类似的区域。超像素通常基于分割方法，其像标准化切割一样在计算上是昂贵的。超像素的不变性水平主要取决于所使用的分割算法。与超像素相比，MSER仅选择最稳定的区域，从而实现高重复性。由于使用了分水岭分割算法，MSER也很有效。在预期会出现极端几何变形的情况下，一个不变的检测器是有益的。否则，它们的尺度不变对应物通常表现更好，特别是对于类别识别[139]。这可以从以下事实来理解：通常可以通过鲁棒性而不是不变性来处理高达30度的视点变化。当从显著不同的视点观察相同的物体时，例如在匹配或检索的背景下，更加频繁的变形。在类别识别的情况下，由于视点变化，对象外观的变化主导变形，并且不变性通常带来很小的改进。

7.3未来的工作
到目前为止，还没有出现任何理论可以提供有关应从图像中提取哪些特征或如何在不管应用的情况下对其进行采样的指导。目前尚不清楚是否有可能对通用特征提取有更原则的理论。
由于存储器要求变得不那么成问题，因此提取各种类型的特征的强力方法（密集地覆盖图像）似乎获得了更好和更好的结果，例如，在对象类别识别中。然而，经常表明，无论系统的后续组件如何，仔细设计图像测量都会带来更好的性能。尽管在特征提取领域已经取得了很多进展 - 特别是在不变性水平方面，尽管使用局部特征构建了令人印象深刻的应用程序，但它们仍然存在许多缺点。我们想再次强调，对于不同的应用，不同的特征属性可能很重要，并且方法的成功在很大程度上取决于适当的特征选择。例如，在从不同观点观察到的场景登记等应用中，基本原理非常清晰，重复性，不变性以及1.4节中定义的特征数量都是至关重要的。在类别识别中，很难确定并测量可重复性，因此对小外观变化的鲁棒性更为重要。

7.3.1有限的重复性
尽管它们取得了成功，但局部特征检测器的可重复性仍然非常有限，重复性分数低于50％是非常常见的（参见例如[145]）。这表明仍有改进的余地。

7.3.2有限的稳健性
所有特征检测器的主要缺点之一是对各种变换的弱鲁棒性，特别是在估计局部尺度和形状方面。

对于小区域，提取方法非常不稳定。它们为大型支撑区域产生稳定的尺度和形状估计，但是其他影响如遮挡和背景杂乱开始影响结果。在各种尺度上提取稳定特征的方法对于各种应用将是非常有益的。

7.3.3缺乏语义解释

在矢量量化之后，这些局部特征通常被称为视觉词或对象部分。然而，这是过于乐观的，因为它们没有任何语义含义。它们只是局部图像片段，其有时仅通过巧合地对应于有意义的对象部分（例如，汽车的轮子）。从纯粹的自下而上的方法来看，这是人们所能想到的。然而，引入自上而下的信息或关于世界的外部知识，可能会发现具有语义意义的对象部分。这可以是中间级别表示的形式，或者是从一组训练数据中学习的新颖的类别特定的局部特征。

7.3.4自动选择最佳特征检测器
有一系列特征检测器可供选择，它们各有优缺点。哪一个表现最好不仅取决于应用程序，还取决于图像内容。为了避免这个问题，研究人员经常并行使用几个探测器。但是，这会对所需的计算时间产生负面影响。可以快速收集一些图像统计数据并建议最合适的探测器的工具将成为时间关键应用的宝贵工具。

7.3.5补充特征

关注特征互补性的新图像测量是另一个探索的方向。由于同时使用多个检测器而产生的过度完整表示仅在有效的多类型特征检测器的情况下才提供临时解决方案。考虑到要处理的数据量的增加，互补检测器或提供用于紧凑表示的互补特征的多类型检测器的有效组合将更加有用。

7.3.6绩效评估

到目前为止，最常用的评估措施是特征的可重复性。虽然这是最重要的属性之一，但它不能保证给定应用程序的高性能。新标准应考虑1.4节中讨论的所有属性。对于生成识别方法至关重要的另一个属性也应该在一般性能评估中得到解决，即特征的重建能力。此外，还需要定义各种探测器的互补性测量。通常，评估在各种应用中提供良好性能预测的特征的更有原则和概率的方式将是有价值的。有足够数量的测试数据强调特征的各个方面，并明确创建用于评估特征检测器。将它组织在一个具有良好定义的测试和标准的共同评估框架中将是有用的。在给定具有特定输入和输出格式的特征检测器的情况下执行广泛评估的自动工具将是非常有用的。

7.4结论

如今，局部特征是一种流行的图像描述工具。它们是宽基线匹配和对象识别的标准表示，既适用于特定对象，也适用于类别级方案。
在本次调查中，我们概述了一些最广泛使用的探测器，对各自的优缺点进行了定性评估，可以在章节和章节的最后找到。通过总结从计算机视觉早期到现在的特征检测的进展，我们还在上下文中进行了局部特征检测的工作。这些来自互联网时代之前的早期作品往往被遗忘。然而，它们包含有价值的见解和想法，可以激发未来对局部特征的研究，并通过重新发明轮子避免浪费资源。文献很多，我们只能触及不同的贡献而不需要详细说明。然而，我们希望提供正确的指针，以便那些感兴趣的人有一个起点，如果他们愿意，可以深入研究。

致谢

作者要感谢卓越网PASCAL和佛兰芒科学研究基金FWO的支持。这项工作也得到了EPSRC EP / F003420 / 1和VIDI-Video IST-2-045547项目的支持。

参考文献

[1] A. Almansa and T. Lindeberg, “Fingerprint enhancement by shape adaptation of scale–space operators with automatic scale selection,” IEEE Transactions on Image Processing, vol. 9, no. 12, pp. 2027–2042, 2000.

[2] L.AlvarezandF.Morales,“Aﬃnemorphologicalmultiscaleanalysisofcorners and multiple junctions,” International Journal of Computer Vision, vol. 2, no. 25, pp. 95–107, 1997.

[3] I. M. Anderson and J. C. Bezdek, “Curvature and tangential deﬂection of discrete arcs: A theory based on the commutator of scatter matrix pairs and its application to vertex detection in planar shape data,” IEEE Transactions on Pattern Analysis and Machine Intelligence, vol. 6, pp. 27–40, 1984.

[4] N. Ansari and E. J. Delp, “On detecting dominant points,” Pattern Recognition, vol. 24, no. 5, pp. 441–451, 1991.

[5] H. Asada and M. Brady, “The curvature primal sketch,” Pattern Analysis and Applications, vol. 8, no. 1, pp. 2–14, 1986.

[6] F. Attneave, “Some informational aspects of visual perception,” Psychological Review, vol. 61, pp. 183–193, 1954.

[7] J.Babaud,A.P.Witkin,M.Baudin,andR.O.Duda,“Uniquenessofthegaussian kernel for scale-space ﬁltering,” IEEE Transactions on Pattern Analysis and Machine Intelligence, vol. 8, no. 1, pp. 26–33, 1986.

[8] S. C. Bae, I.-S. Kweon, and C. Don Yoo, “COP: A new corner detector,” Pattern Recognition Letters, vol. 23, no. 11, pp. 1349–1360, 2002.

[9] R. Bajcsy, “Computer identiﬁcation of visual surface,” Computer and Graphics Image Processing, vol. 2, pp. 118–130, 1973.

[10] R. Bajcsy and D. A. Rosenthal, Visual and Conceptual Focus of Attention Structured Computer Vision. Academic Press, 1980.
[11] J. Bala, K. DeJong, J. Huang, H. Vafaie, and H. Wechsler, “Using learning to facilitate the evolution of features for recognizing visual concepts,” Evolutionary Computation, vol. 4, no. 3, pp. 297–311, 1996.

[12] J. Bauer, H. Bischof, A. Klaus, and K. Karner, “Robust and fully automated image registration using invariant features,” International Society for Photogrammetry and Remote Sensing, 2004.

[13] A. Baumberg, “Reliable feature matching across widely separated views,” in Proceedings of the Conference on Computer Vision and Pattern Recognition, pp. 774–781, 2000.

[14] H. Bay, A. Ess, T. Tuytelaars, and L. Van Gool, “Speeded-up robust features (SURF),” International Journal on Computer Vision and Image Understanding, vol. 110, no. 3, pp. 346–359, 2008.

[15] H. Bay, T. Tuytelaars, and L. Van Gool, “SURF: Speeded up robust features,” in Proceedings of the European Conference on Computer Vision, pp. 404–417, 2006.

[16] P. R. Beaudet, “Rotationally invariant image operators,” in Proceedings of the International Joint Conference on Pattern Recognition, pp. 579–583, 1978.

[17] S. Belongie, J. Malik, and J. Puzicha,, “Shape context: A new descriptor for shape matching and object recognition,” in Proceedings of the Neural Information Processing Systems, pp. 831–837, 2000.

[18] H. L. Beus and S. S. H. Tiu, “An improved corner detection algorithm based on chain-coded plane curves,” Pattern Recognition, vol. 20, no. 3, pp. 291–296, 1987.

[19] D. J. Beymer, “Finding junctions using the image gradient,” in International Conference Computer Vision and Pattern Recognition, pp. 720–721, 1991.

[20] I. Biederman, “Recognition-by-components: A theory of human image understanding,” Psychological Review, vol. 2, no. 94, pp. 115–147, 1987.

[21] Y. Boykov and M.-P. Jolly, “Interactive graph cuts for optimal boundary & region segmentation of objects in N–D images,” in Proceedings of the International Conference on Computer Vision, vol. 1, pp. 105–112, 2001.

[22] P. Brand and R. Mohr, “Accuracy in image measure,” SPIE Conference on Videometrics III, vol. 2350, pp. 218–228, 1994.

[23] V. Brecher, R. Bonner, and C. Read, “A model of human preattentive visual detection of edge orientation anomalies,” in Proceedings of the SPIE Conference of Visual Information Processing: From Neurons to Chips, vol. 1473, pp. 39–51, 1991.

[24] L. Bretzner and T. Lindeberg, “Feature tracking with automatic selection of spatial scales,” Computer Vision and Image Understanding, vol. 71, no. 3, pp. 385–392, 1998.

[25] C. R. Brice and C. L. Fennema, “Scene analysis using regions,” Artiﬁcial Intelligence, vol. 1, pp. 205–226, 1970.

[26] M. Brown and D. Lowe, “Recognising panoramas,” in Proceedings of the International Conference on Computer Vision, pp. 1218–1227, 2003.

[27] P. J. Burt and E. H. Adelson, “The laplacian pyramid as a compact image code,” IEEE Transactions on Communications, vol. 9, no. 4, pp. 532–540, 1983.

[28] C. Cabani and W. J. MacLean, “Implementation of an aﬃne-covariant feature detector in ﬁeld-programmable gate arrays,” in Proceedings of the International Conference on Computer Vision Systems, 2007.

[29] J. Canny, “A computational approach to edge detection,” IEEE Transactions on Pattern Analysis and Machine Intelligence, vol. 8, no. 6, pp. 679–698, 1986.

[30] P. Carbonetto, N. de Freitas, and K. Barnard, “A statistical model for general contextual object recognition,” in Proceedings of the European Conference on Computer Vision, part I, pp. 350–362, 2004.

[31] C. Carson, S. Belongie, S. Greenspan, and J. Malik, “Blobworld: Image segmentation using expectation-maximization and its application to image querying,” IEEE Transactions on Pattern Analysis and Machine Intelligence, vol. 24, no. 8, pp. 1026–1038, 2002.

[32] K. R. Cave and J. M. Wolfe, “Modeling the role of parallel processing in visual search,” Cognitive Psychology, vol. 22, pp. 225–271, 1990.

[33] S. P. Chang and J. H. Horng, “Corner point detection using nest moving average,” Pattern Recognition, vol. 27, no. 11, pp. 1533–1537, 1994.

[34] D. Chapman, “Vision, instruction and action,” Technical Report AI-TR-1204, AI Laboratory, MIT, 1990.

[35] C.-H. Chen, J.-S. Lee, and Y.-N. Sun, “Wavelet transformation for gray-level corner detection,” Pattern Recognition, vol. 28, no. 6, pp. 853–861, 1995.

[36] M. Chen and P. Yan, “A multiscaling approach based on morphological ﬁltering,” IEEE Transactions on Pattern Analysis and Machine Intelligence, vol. 1, no. 7, pp. 694–700, 1989.

[37] W.-C. Chen and P. Rockett, “Bayesian labelling of corners using a grey–level corner image mode,” in Proceedings of the International Conference on Image Processing, pp. 687–690, 1997.

[38] O. Chomat, V. Colin deVerdi`ere, D. Hall, and J. Crowley, “Local scale selection for gaussian based description techniques,” in Proceedings of the European Conference on Computer Vision, Dublin, Ireland, pp. 117–133, 2000.

[39] J. J. Clark and N. J. Ferrier, “Modal control of attentive vision system,” in Proceedings of the International Conference on Computer Vision, pp. 514–523, 1988.

[40] C. Coelho, A. Heller, J. L. Mundy, D. A. Forsyth, and A. Zisserman, An Experimental Evaluation of Projective Invariants. Cambridge, MA: MIT Press, 1992.

[41] J. Cooper, S. Venkatesh, and L. Kitchen, “The dissimilarity corner detectors,” International Conference on Advanced Robotics, pp. 1377–1382, 1991.

[42] J. Cooper, S. Venkatesh, and L. Kitchen, “Early jump-out corner detectors,” IEEE Transactions on Pattern Analysis and Machine Intelligence, vol. 15, no. 8, pp. 823–828, 1993.

[43] T. F. Cootes and C. Taylor, “Performance evaluation of corner detection algorithms under aﬃne and similarity transforms,” in Proceedings of the British Machine Vision Conference, 2001.

[44] J. J. Corso and G. D. Hager, “Coherent regions for concise and stable image description,” in Proceedings of the Conference on Computer Vision and Pattern Recognition, vol. 2, pp. 184–190, 2005.

[45] J. C. Cottier,, “Extraction et appariements robustes des points d’int´erˆet de deux images non etalonn´ees,” Technical Report, LIFIA-IMAG-INRIA, RhoneAlpes, 1994. [46] T. Cour and J. Shi, “Recognizing objects by piecing together the segmentation puzzle,” in Proceedings of the Conference on Computer Vision and Pattern Recognition, 2007.

[47] J. L. Crowley and A. C. Parker, “A representation for shape based on peaks and ridges in the diﬀerence of low pass transform,” IEEE Transactions on Pattern Analysis and Machine Intelligence, vol. 6, no. 2, pp. 156–170, 1984.

[48] J. L. Crowley and A. C. Sanderson, “Multiple resolution representation and probabilisticmatchingof2Dgray–scaleshape,”IEEE Transactions on Pattern Analysis and Machine Intelligence, vol. 9, no. 1, pp. 113–121, 1987.

[49] S. M. Culhane and J. Tsotsos, “An attentional prototype for early vision,” in Proceedings of the European Conference on Computer Vision, pp. 551–560, 1992.

[50] D. Cyganski and J. A. Or, “Application of tensor theory to object recognition and orientation determination,” IEEE Transactions on Pattern Analysis and Machine Intelligence, vol. 7, pp. 662–673, 1985.

[51] E. R. Davies, “Application of the generalised hough transform to corner detection,” IEE Proceedings, vol. 135, no. 1, pp. 49–54, 1988.

[52] R. Deriche and T. Blaszka, “Recovering and characterizing image features using an eﬃcient model-based approach,” in Proceedings of the Conference on Computer Vision and Pattern Recognition, pp. 530–535, 1993.

[53] R. Deriche and G. Giraudon, “Accurate corner detection: An analytical study,” in Proceedings International Conference on Computer Vision, pp. 66– 70, 1990.

[54] R.DericheandG.Giraudon,“Acomputationalapproachforcornerandvertex detection,” International Journal of Computer Vision, vol. 10, no. 2, pp. 101– 124, 1993.

[55] P. Dias, A. Kassim, and V. Srinivasan, “A neural network based corner detection method,” in IEEE International Conference on Neural Networks, vol. 4, pp. 2116–2120, 1995.

[56] M. Donoser and H. Bischof, “Eﬃcient maximally stable extremal region (MSER) tracking,” in Proceedings of the Conference on Computer Vision and Pattern Recognition, pp. 553–560, 2006.

[57] L. Dreschler and H. Nagel, “Volumetric model and 3D-trajectory of a moving car derived from monocular TV-frame sequence of a street scene,” In Computer Graphics and Image Processing, vol. 20, pp. 199–228, 1982.

[58] R. Duda and P. Hart, Pattern Classiﬁcation and Scene Analysis. Wiley– Interscience, 1973.

[59] Y. Dufournaud, C. Schmid, and R. Horaud, “Matching images with diﬀerent resolutions,” in Proceedings of the Conference on Computer Vision and Pattern Recognition, pp. 612–618, 2000.

[60] J. Dunham, “Optimum uniform piecewise linear approximation of planar curves,” IEEE Transactions on Pattern Analysis and Machine Intelligence, vol. 8, no. 1, pp. 67–75, 1986.

[61] J. Q. Fang and T. S. Huang, “A corner ﬁnding algorithm for image analysis and registration,” in Proceedings of AAAI Conference, pp. 46–49, 1982.

[62] L. FeiFei and P. Perona, “A Bayesian hierarchical model for learning natural scene categories,” in Proceedings of the Conference on Computer Vision and Pattern Recognition, vol. 2, pp. 524–531, 2005.

[63] F. Y. Feng and T. Pavlidis, “Finding ‘vertices’ in a picture,” Computer Graphics and Image Processing, vol. 2, pp. 103–117, 1973.

[64] F. Y. Feng and T. Pavlidis, “Decomposition of polygons into simpler components: Feature generation for syntactic pattern recognition,” IEEE Transactions on Computers, vol. C-24, 1975.

[65] R. Fergus, P. Perona, and A. Zisserman, “Object class recognition by unsupervised scale-invariant learning,” in Proceedings of the Conference on Computer Vision and Pattern Recognition, pp. 264–271, 2003.

[66] V. Ferrari, T. Tuytelaars, and L. Van Gool, “Simultaneous object recognition and segmentation by image exploration,” in Proceedings of the European Conference on Computer Vision, pp. 40–54, 2004.

[67] L. M. J. Florack, B. M. ter Haar Romeny, J. J. Koenderink, and M. A. Viergever, “Scale and the diﬀerential structure of images,” Image and Vision Computing, vol. 10, pp. 376–388, 1992.

[68] P.-E. Forssen and D. Lowe, “Shape descriptors for maximally stable extremal regions,” in Proceedings of the International Conference on Computer Vision, pp. 59–73, 2007.

[69] W. F¨orstner, “A framework for low level feature extraction,” in Proceedings of the European Conference on Computer Vision, pp. 383–394, 1994.

[70] W. F¨orstner and E. G¨ulch, “A fast operator for detection and precise location of distinct points, corners and centres of circular features,” in Intercommission Conference on Fast Processing of Photogrammetric Data, pp. 281–305, 1987.

[71] F. Fraundorfer and H. Bischof, “Evaluation of local detectors on non-planar scenes,” in Proceedings of the Austrian Association for Pattern Recognition Workshop, pp. 125–132, 2004.

[72] H. Freeman, “A review of relevant problems in the processing of line-drawing data,” in Automatic Interpretation and Classiﬁcation of Images, (A. Graselli, ed.), pp. 155–174, Academic Press, 1969.

[73] H. Freeman, “Computer processing of line drawing images,” Surveys, vol. 6, no. 1, pp. 57–97, 1974.

[74] H. Freeman and L. S. Davis, “A corner-ﬁnding algorithm for chain-coded curves,” IEEE Transactions on Computers, vol. 26, pp. 297–303, 1977.

[75] M. Galun, E. Sharon, R. Basri, and A. Brandt, “Texture segmentation by multiscale aggregation of ﬁlter responses and shape elements,” in Proceedings of the International Conference on Computer Vision, vol.2,pp.716–725,2003.

[76] P. Gaussier and J. P. Cocquerez, “Neural networks for complex scene recognition: Simulation of a visual system with several cortical areas,” in Proceedings of the International Joint Conference on Neural Networks, vol. 3, pp. 233–259, 1992.

[77] S. Ghosal and R. Mehrotra, “Zernike moment–based feature detectors,” in International Conference on Image Processing, pp. 934–938, 1994.

[78] G. J. Gieﬁng, H. Janssen, and H. Mallot, “Saccadic object recognition with an active vision system,” in Proceedings of the European Conference on Artiﬁcial Intelligence, pp. 803–805, 1992.

[79] S. Gilles, Robust Description and Matching of Image. PhD thesis, University of Oxford, 1998.

[80] V. Gouet, P. Montesinos, R. Deriche, and D. Pel´e, “Evaluation de d´etecteurs de points d’int´erˆet pour la couleur,” in 12`eme Congr`es Francophone AFRIF– AFIA de Reconnaissance des Formes et Intelligence Artiﬁcielle, pp. 257–266, 2000.

[81] S. Grossberg, E. Mingolla, and D. Todorovic, “A neural network architecture for preattentive vision,” IEEE Transactions on Biomedical Engineering, vol. 36, pp. 65–84, 1989.

[82] A. Guidicci, “Corner characterization by diﬀerential geometry techniques,” Pattern Recognition Letters, vol. 8, no. 5, pp. 311–318, 1988.

[83] R. M. Haralick and L. G. Shapiro, Computer and Robot Vision. AddisonWesley, pp. 453–507, 1993.

[84] C. Harris and M. Stephens, “A combined corner and edge detector,” in Alvey Vision Conference, pp. 147–151, 1988.

[85] T. I. Hashimoto, S. Tsujimoto, and S. Arimoto, “Spline approximation of line images by modiﬁed dynamic programming,” Transactions of IECE of Japan, vol. J68, no. 2, pp. 169–176, 1985.

[86] X. C. He and N. H. C. Yung, “Curvature scale space corner detector with adaptive threshold and dynamic region of support,” in International Conference on Pattern Recognition, pp. 791–794, 2004.

[87] F. Heitger, L. Rosenthaler, R. von der Heydt, E. Peterhans, and O. Kubler, “Simulation of neural contour mechanisms: From simple to end-stopped cells,” Vision Research, vol. 32, no. 5, pp. 963–981, 1992.

[88] A. Heyden and K. Rohr, “Evaluation of corner extraction schemes using invariance method,” in Proceedings of the International Conference on Pattern Recognition, pp. 895–899, 1996.

[89] S. Heymann, K. Maller, A. Smolic, B. Froehlich, and T. Wiegand, “SIFT implementation and optimization for general-purpose GPU,” in Proceedings of the International Conference in Central Europe on Computer Graphics, Visualization and Computer Vision, 2007.

[90] J. Hong and X. Tan, “A new approach to point pattern matching,” in Proceedings of the International Conference on Pattern Recognition, vol. 1, pp. 82–84, 1988.

[91] R. Horaud, T. Skordas, and F. Veillon, “Finding geometric and relational structures in an image,” in Proceedings of the European Conference on Computer Vision, pp. 374–384, 1990.

[92] D. Hubel and T. Wiesel, “Receptive ﬁelds, binocular interaction and functional architecture in the cat’s visual cortex,” Journal of Physiology, vol. 160, pp. 106–154, 1962.

[93] L. Itti and C. Koch, “Computational modeling of visual attention,” Nature Reviews Neuroscience, vol. 2, no. 3, pp. 194–203, 2001.

[94] L. Itti, C. Koch, and E. Niebur, “A model of saliency-based visual attention for rapid scene analysis,” IEEE Transactions on Pattern Analysis and Machine Intelligence, vol. 20, pp. 1254–1259, 1998.

[95] Q. Ji and R. M. Haralick, “Corner detection with covariance propagation,” in Proceedings of the Conference on Computer Vision and Pattern Recognition, pp. 362–367, 1997.

[96] B. Julesz, “Textons, the elements of texture perception, and their interactions,” Nature, vol. 290, pp. 91–97, 1981.

[97] F. Jurie and B. Triggs, “Creating eﬃcient codebooks for visual recognition,” in Proceedings of the International Conference on Computer Vision, pp. 604– 610, 2005.

[98] T. Kadir and M. Brady, “Scale, saliency and image description,” International Journal of Computer Vision, vol. 45, no. 2, pp. 83–105, 2001.

[99] T. Kadir, M. Brady, and A. Zisserman, “An aﬃne invariant method for selecting salient regions in images,” in Proceedings of the European Conference on Computer Vision, pp. 345–457, 2004.

[100] Y. Ke and R. Sukthankar, “PCA–SIFT: A more distinctive representation for local image descriptors,” in Proceedings of the Conference on Computer Vision and Pattern Recognition, pp. 511–517, 2004.

[101] C. Kenney, B. Manjunath, M. Zuliani, G. Hewer, and A. Van Nevel, “A condition number for point matching with application to registration and postregistration error estimation,” IEEE Transactions on Pattern Analysis and Machine Intelligence, vol. 25, no. 11, pp. 1437–1454, 2003.

[102] C. S. Kenney, M. Zuliani, and B. S. Manjunath, “An axiomatic approach to corner detection,” International Conference on Computer Vision and Pattern Recognition, pp. 191–197, 2005.

[103] W. Kienzle, F. A. Wichmann, B. Scholkopf, and M. O. Franz, “Learning an interest operator from human eye movements,” in Proceedings of the Conference on Computer Vision and Pattern Recognition Workshop, pp. 1–8, 2005.

[104] L. Kitchen and A. Rosenfeld, “Gray-level corner detection,” Pattern Recognition Letters, vol. 1, pp. 95–102, 1982.

[105] C. Koch and S. Ullman, “Shifts in selective visual attention: Towards the underlying neural circuitry,” Human Neurobiology, vol. 4, no. 4, pp. 219–227, 1985.

[106] J. J. Koenderink, “The structure of images,” Biological Cybernetics, vol. 50, pp. 363–396, 1984.

[107] R. Laganiere, “A morphological operator for corner detection,” Pattern Recognition, vol. 31, no. 11, pp. 1643–1652, 1998.

[108] D. J. Langridge, “Curve encoding and detection of discontinuities,” Computer Graphics Image Processing, vol. 20, pp. 58–71, 1982.

[109] I. Laptev and T. Lindeberg, “Tracking of multi-state hand models using particle ﬁltering and a hierarchy of multi-scale image features,” in Proceedings of Scale-Space and Morphology Workshop, pp. 63–74, Lecture Notes in Computer Science, 2001.

[110] S. Lazebnik, C. Schmid, and J. Ponce, “Sparse texture representation using aﬃneinvariantneighborhoods,”inProceedings of the Conference on Computer Vision and Pattern Recognition, pp. 319–324, 2003.

[111] J. S. Lee, Y. N. Sun, C. H. Chen, and C. T. Tsai, “Wavelet based corner detection,” Pattern Recognition, vol. 26, pp. 853–865, 1993.

[112] V. Lepetit and P. Fua, “Keypoint recognition using randomized trees,” IEEE Transactions on Pattern Analysis and Machine Intelligence, vol. 28, no. 9, pp. 1465–1479, 2006.

[113] L. Li and W. Chen, “Corner detection and interpretation on planar curves using fuzzy reasoning,” IEEE Transactions on Pattern Analysis and Machine Intelligence, vol. 21, no. 11, pp. 1204–1210, 1999.

[114] R.-S. Lin, C.-H. Chu, and Y.-C. Hsueh, “A modiﬁed morphological corner detector,” Pattern Recognition Letters, vol. 19, no. 3, pp. 279–286, 1998.

[115] T. Lindeberg, “Scale-space for discrete signals,” IEEE Transactions on Pattern Analysis and Machine Intelligence, vol. 12, no. 1, pp. 234–254, 1990.

[116] T. Lindeberg, “Detecting salient blob-like image structures and their scales with a scale-space primal sketch – a method for focus-of-attention,” International Journal of Computer Vision, vol. 11, no. 3, pp. 283–318, 1993.

[117] T. Lindeberg, Scale-Space Theory in Computer Vision. Kluwer Academic Publishers, 1994.

[118] T. Lindeberg, “Direct estimation of aﬃne image deformation using visual front-end operations with automatic scale selection,” in Proceedings of the International Conference on Computer Vision, pp. 134–141, 1995.

[119] T. Lindeberg, “Edge detection and ridge detection with automatic scale selection,” International Journal of Computer Vision, vol. 30, no. 2, pp. 79–116, 1998.

[120] T. Lindeberg, “Feature detection with automatic scale selection,” International Journal of Computer Vision, vol. 30, no. 2, pp. 79–116, 1998.

[121] T. Lindeberg and J. Garding, “Shape-adapted smoothing in estimation of 3-D shape cues from aﬃne deformations of local 2-D brightness structure,” Image and Vision Computing, vol. 15, no. 6, pp. 415–434, 1997.

[122] H. Ling and D. Jacobs, “Deformation invariant image matching,” in Proceedings of the International Conference on Computer Vision, vol. 2, pp. 1466– 1473, 2005.

[123] S.-T. Liu and W.-H. Tsai, “Moment preserving corner detection,” Pattern Recognition, vol. 23, no. 5, pp. 441–460, 1990.

[124] D. Lowe, “Distinctive image features from scale-invariant keypoints,” International Journal of Computer Vision, vol. 2, no. 60, pp. 91–110, 2004.

[125] D. G. Lowe, “Organization of smooth image curves at multiple scales,” International Conference on Computer Vision, pp. 558–567, 1988.

[126] D. G. Lowe, “Object recognition from local scale-invariant features,” in Proceedings of the International Conference on Computer Vision, pp. 1150–1157, 1999.

[127] G. Loy and A. Zelinsky, “Fast radial symmetry for detecting points of interest,” IEEE Transactions on Pattern Analysis and Machine Intelligence, vol. 25, no. 8, pp. 959–973, 2003.

[128] B. Luo, A. D. J. Cross, and E. R. Hancock, “Corner detection via topographic analysis of vector potential,” Pattern Recognition Letters, vol. 20, no. 6, pp. 635–650, 1998.

[129] J. Malik, S. Belongie, J. Shi, and T. Leung, “Textons, contours and regions: Cue integration in image segmentation,” in Proceedings of the International Conference on Computer Vision, pp. 918–925, 1999.

[130] J. Malik and P. Perona, “Preattentive texture discrimination with early vision mechanism,” Journal of Optical Society of America A, vol. 7, no. 5, pp. 923– 932, 1990.

[131] B. S. Manjunath, C. Shekhar, and R. Chellappa, “A new approach to image feature detection with applications,” Pattern Recognition, vol. 29, no. 4, pp. 627–640, 1996.

[132] R. Maree, P. Geurts, J. Piater, and L. Wehenkel, “Random subwindows for robust image classiﬁcation,” in Proceedings of the Conference on Computer Vision and Pattern Recognition, vol. 1, pp. 34–40, 2005.

[133] D. Marr, Vision. USA, San Francisco, CA: W.H. Freeman and Company, 1982.

[134] J. Matas, O. Chum, M. Urban, and T. Pajdla, “Robust wide-baseline stereo from maximally stable extremal regions,” in Proceedings of the British Machine Vision Conference, pp. 384–393, 2002.

[135] J. Matas, S. Obdrzalek, and O. Chum, “Local aﬃne frames for wide-baseline stereo,” in Proceedings of 16th International Conference Pattern Recognition, vol. 4, pp. 363–366, 2002.

[136] G. Medioni and Y. Yasumoto, “Corner detection and curve representation using cubic B-spline,” Computer Vision, Graphics and Image Processing, vol. 39, no. 1, pp. 267–278, 1987.

[137] R. Mehrotra, S. Nichani, and N. Ranganathan, “Corner detection,” Pattern Recognition, vol. 23, no. 11, pp. 1223–1233, 1990.

[138] K. Mikolajczyk, Scale and Aﬃne Invariant Interest Point Detectors. PhD thesis, 2002. INRIA Grenoble.

[139] K.Mikolajczyk,B.Leibe,andB.Schiele,“Localfeaturesforobjectclassrecognition,” in Proceedings of the International Conference on Computer Vision, pp. 525–531, 2005.

[140] K. Mikolajczyk, B. Leibe, and B. Schiele, “Multiple object class detection with a generative model,” in Proceedings the Conference on Computer Vision and Pattern Recognition, pp. 26–36, 2006.

[141] K. Mikolajczyk and C. Schmid, “Indexing based on scale-invariant interest points,” in Proceedings of the International Conference on Computer Vision, pp. 525–531, Vancouver, Canada, 2001.

[142] K. Mikolajczyk and C. Schmid, “An aﬃne invariant interest point detector,” in Proceedings of the European Conference on Computer Vision, pp. 128–142, 2002.

[143] K.MikolajczykandC.Schmid,“Scaleandaﬃneinvariantinterestpointdetectors,” International Journal of Computer Vision, vol. 1, no. 60, pp. 63–86, 2004.

[144] K. Mikolajczyk and C. Schmid, “A performance evaluation of local descriptors,” IEEE Transactions on Pattern Analysis and Machine Intelligence, vol. 27, no. 10, pp. 1615–1630, 2005.

[145] K. Mikolajczyk, T. Tuytelaars, C. Schmid, A. Zisserman, J. Matas, F. Schaffalitzky, T. Kadir, and L. Van Gool, “A comparison of aﬃne region detectors,” International Journal of Computer Vision, vol. 65, no. 1/2, pp. 43–72, 2005.

[146] K. Mikolajczyk, A. Zisserman, and C. Schmid, “Shape recognition with edge based features,” in Proceedings of the British Machine Vision Conference, pp. 779–788, 2003.

[147] R. Milanese, Detecting Salient Regions in an Image: From Biological Evidence to Computer Implementation. PhD thesis, University of Geneva, 1993.

[148] R.Milanese,J.-M.Bost,andT.Pun,“Abottom-upattentionsystemforactive vision,” in Proceedings of the European Conference on Artiﬁcial Intelligence, pp. 808–810, 1992.

[149] D. Milgram, “Computer methods for creating photomosaics,” IEEE Transactions on Computers, vol. 23, pp. 1113–1119, 1975.

[150] F. Mohanna and F. Mokhtarian, “Performance evaluation of corner detection algorithms under aﬃne and similarity transforms,” in Proceedings of the British Machine Vision Conference, 2001.

[151] F. Mokhtarian and A. Mackworth, “Scale-based description of plannar curves and two-dimensional shapes,” IEEE Transactions on Pattern Analysis and Machine Intelligence, vol. 8, no. 1, pp. 34–43, 1986.

[152] F. Mokhtarian and R. Suomela, “Robust image corner detection through curvature scale-space,” IEEE Transactions on Pattern Analysis and Machine Intelligence, vol. 20, no. 12, pp. 1376–1381, 1998.

[153] P. Montesinos, V. Gouet, and R. Deriche, “Diﬀerential invariants for color images,” in Proceedings of the International Conference on Pattern Recognition, pp. 838–840, 1998.

[154] H. Moravec, “Towards automatic visual obstacle avoidance,” in Proceedings of the International Joint Conference on Artiﬁcial Intelligence, pp. 584–590, 1977.

[155] H. Moravec, “Visual mapping by a robot rover,” in Proceedings of the International Joint Conference on Artiﬁcial Intellingence, pp. 598–600, 1979.

[156] H. Moravec, “Rover visual obstacle avoidance,” in Proceedings of the International Joint Conference on Artiﬁcial Intelligence, pp. 785–790, 1981.

[157] P. Moreels and P. Perona, “Evaluation of features detectors and descriptors based on 3D objects,” in Proceedings of the International Conference on Computer Vision, pp. 800–807, 2005.

[158] P. Moreels and P. Perona, “Evaluation of features detectors and descriptors based on 3D objects,” International Journal of Computer Vision, vol. 73, no. 3, pp. 800–807, 2007.

[159] G. Mori, X. Ren, A. Efros, and J. Malik, “Recovering human body conﬁgurations: Combining segmentation and recognition,” in Proceedings of the Conference on Computer Vision and Pattern Recognition, vol. 2, pp. 326–333, 2004.

[160] H. Murase and S. Nayar, “Visual learning and recognition of 3D objects from appearance,” International Journal on Computer Vision, vol. 14, no. 1, pp. 5– 24, 1995.

[161] E. Murphy-Chutorian and M. Trivedi, “N-tree disjoint-set forests for maximally stable extremal regions,” in Proceedings of the British Machine Vision Conference, 2006. [162] J. Mutch and D. G. Lowe, “Multiclass object recognition with sparse, localized features,” in Proceedings of the Conference on Computer Vision and Pattern Recognition, pp. 11–18, 2006.

[163] H. H. Nagel, “Displacement vectors derived from second-order intensity variations in image sequences,” Computer Vision Graphics, and Image Processing, vol. 21, pp. 85–117, 1983.

[164] M. Nakajima, T. Agui, and K. Sakamoto, “Pseudo-coding method for digital line ﬁgures,” Transactions of the IECE, vol. J68–D, no. 4, pp. 623–630, 1985.

[165] U. Neisser, “Visual search,” Scientiﬁc American, vol. 210, no. 6, pp. 94–102, 1964.

[166] D. Nister and H. Stewenius, “Scalable recognition with a vocabulary tree,” in Proceedings of the Conference on Computer Vision and Pattern Recognition, pp. 2161–2168, 2006.

[167] J. A. Noble, “Finding corners,” Image and Vision Computing, vol. 6, no. 2, pp. 121–128, 1988.

[168] J. A. Noble, Descriptions of Image Surfaces. PhD thesis, Department of Engineering Science, Oxford University, 1989.

[169] E. Nowak, F. Jurie, and B. Triggs, “Sampling strategies for bag-of-features image classiﬁcation,” in Proceedings of the European Conference on Computer Vision, pp. 490–503, 2006.

[170] H. Ogawa, “Corner detection on digital curves based on local symmetry of the shape,” Pattern Recognition, vol. 22, no. 4, pp. 351–357, 1989.

[171] C.M.OrangeandF.C.A.Groen,“Model-basedcornerdetection,”in Proceedings of the Conference on Computer Vision and Pattern Recognition, pp. 690– 691, 1993.

[172] M. Pabst, H. J. Reitboeck, and R. Eckhorn, “A model of preattentive Region deﬁnition based on texture analysis,” in Models of Brain Function, pp. 137– 150, Cambridge, England: Cambridge University Press, 1989.

[173] K. Paler, J. Foglein, J. Illingworth, and J. Kittler, “Local ordered grey levels as an aid to corner detection,” Pattern Recognition, vol. 17, no. 5, pp. 535–543, 1984.

[174] T. Pavlidis, Structural Pattern Recognition. Berlin, Heidelberg, NY: SpringerVerlag, 1977.

[175] T. Pavlidis, Algorithms for Graphics and Image Processing. Computer Science Press, 1982.

[176] T. Pavlidis, “Problems in recognition of drawings,” Syntactic and Structural Pattern Recognition, vol. 45, pp. 103–113, 1988.

[177] M. Perdoch, J. Matas, and S. Obdrzalek, “Stable aﬃne frames on isophotes,” in Proceedings of the International Conference on Computer Vision, 2007.

[178] J. R. Quinlan, “Induction of decision trees,” Machine Learning, vol. 1, pp. 81– 106, 1986.

[179] P. Rajan and J. Davidson, “Evaluation of corner detection algorithms,” in 21th Southeastern Symposium on System Theory, pp. 29–33, 1989.

[180] K. Rangarajan, M. Shah, and D. V. Brackle, “Optimal corner detection,” Computer Vision Graphics Image Processing, vol. 48, pp. 230–245, 1989.

[181] A. Rattarangsi and R. T. Chin, “Scale-based detection of corners of planar curves,” IEEE Transactions on Pattern Analysis and Machine Intelligence, vol. 14, pp. 430–449, 1992.

[182] D. Reisfeld, H. Wolfson, and Y. Yeshurun, “Context free attentional operators: The generalized symmetry transform,” International Journal of Computer Vision, vol. 14, no. 2, pp. 119–130, 1995.

[183] X. Ren, C. Fowlkes, and J. Malik, “Scale–invariant contour completion using conditional random ﬁelds,” in Proceedings of the International Conference on Computer Vision, vol. 2, pp. 1214–1221, 2005.

[184] X. Ren and J. Malik, “Learning a classiﬁcation model for segmentation,” in Proceedings of the International Conference on Computer Vision, vol. 1, pp. 10–17, 2003.

[185] M. Riesenhuber and T. Poggio, “Hierarchical models of object recognition in cortex,” Nature Neuroscience, vol. 2, pp. 1019–1025, 1999.

[186] B. Robbins and R. A. Owens, “2D feature detection via local energy,” Image Vision Comput, vol. 15, no. 5, pp. 353–368, 1997.

[187] V. Roberto and R. Milanese, “Matching hierarchical structures in a machine vision system,” Intelligent Autonomous Systems, pp. 845–852, 1989.

[188] K. Rohr, “Recognizing corners by ﬁtting parametric models,” International Journal of Computer Vision, vol. 9, no. 3, pp. 213–230, 1992.

[189] K. Rohr, “Localization properties of direct corner detectors,” Journal of Mathematical Imaging and Vision, vol. 4, no. 2, pp. 139–150, 1994.

[190] K. Rohr, “On the precision in estimating the location of edges and corners,” Journal of Mathematical Imaging and Vision, vol. 7, no. 1, pp. 7–22, 1997.

[191] A. Rosenfeld, “Picture processing by computer,” ACM Computing Surveys, vol. 1, no. 3, pp. 147–176, 1969.

[192] A. Rosenfeld, “Digital image processing and recognition,” Digital Image Processing, pp. 1–11, 1977.

[193] A. Rosenfeld and E. Johnston, “Angle detection on digital curves,” IEEE Transactions on Computers, vol. C-22, pp. 875–878, 1973.

[194] A. Rosenfeld and A. C. Kak, Digital Picture Processing. Academic Press, Second Edition, 1982.

[195] A. Rosenfeld and M. Thurston, “Edge and curve detection for digital scene analysis,” IEEE Transactions on Computers, vol. C-20, pp. 562–569, 1971.

[196] A. Rosenfeld, M. Thurston, and Y. H. Lee, “Edge and curve detection: Further experiments,” IEEE Transactions on Computers, vol. C-21, pp. 677–715, 1972.

[197] A. Rosenfeld and J. S. Weszka, “An improved method of angle detection on digital curves,” IEEE Transactions on Computers, vol. 24, no. 9, pp. 940–941, 1975.

[198] L. Rosenthaler, F. Heitger, O. Kubler, and R. von der Heydt, “Detection of general edges and keypoints,” in Proceedings of the European Conference on Computer Vision, pp. 78–86, 1992.

[199] P.L.Rosin,“Representingcurvesattheirnaturalscales,” Pattern Recognition, vol. 25, pp. 1315–1325, 1992.

[200] P. L. Rosin, “Determining local natural scales of curves,” International Conference on Pattern Recognition, 1994.

[201] P. L. Rosin, “Measuring corner properties,” Computer Vision and Image Understanding, vol. 73, no. 2, pp. 292–307, 1999.

[202] E. Rosten and T. Drummond, “Fusing points and lines for high performance tracking,” in Proceedings of the International Conference on Computer Vision, pp. 1508–1511, 2005.

[203] E. Rosten and T. Drummond, “Machine learning for high-speed corner detection,” in Proceedings of the European Conference on Computer Vision, pp. 430–443, 2006.

[204] C. A. Rothwell, A. Zisserman, D. A. Forsyth, and J. L. Mundy, “Planar object recognition using projective shape representation,” International Journal on Computer Vision, vol. 16, pp. 57–99, 1995.

[205] W. S. Rutkowski and A. Rosenfeld, “A comparison of corner detection techniques for chain coded curves,” Technical Report 623, Maryland University, 1978.

[206] P. A. Sandon, “Simulating visual attention,” Journal of Cognitive Neuroscience, vol. 2, no. 3, pp. 213–231, 1990.

[207] P. V. Sankar and C. V. Sharma, “A parallel procedure for the detection of dominant points on digital curves,” Computer Graphics and Image Processing, vol. 7, pp. 403–412, 1978.

[208] F. Schaﬀalitzky and A. Zisserman, “Viewpoint invariant texture matching and wide baseline stereo,” in Proceedings of the International Conference on Computer Vision, pp. 636–643, 2001.

[209] F. Schaﬀalitzky and A. Zisserman, “Multi-view matching for unordered image sets,” in Proceedings of the European Conference on Computer Vision, pp. 414–431, 2002.

[210] B. Schiele and J. L. Crowley, “Probabilistic object recognition using multidimensional receptive ﬁeld histograms,” in Proceedings of the International Conference on Pattern Recognition, vol. 2, pp. 50–54, 1996.

[211] B. Schiele and J. L. Crowley, “Recognition without correspondence using multi-dimensional receptive ﬁeld histograms,” International Journal of Computer Vision, vol. 36, no. 1, pp. 31–50, 2000.

[212] C. Schmid and R. Mohr, “Combining gray-value invariants with local constraints for object recognition,” in Proceedings of the Conference on Computer Vision and Pattern Recognition, pp. 872–877, 1996.

[213] C. Schmid and R. Mohr, “Local gray-value invariants for image retrieval,” IEEE Transactions on Pattern Analysis and Machine Intelligence, vol. 19, no. 5, pp. 530–534, 1997.

[214] C. Schmid, R. Mohr, and C. Bauckhage, “Comparing and evaluating interest points,” in Proceedings of the International Conference on Computer Vision, pp. 230–235, 1998.

[215] C. Schmid, R. Mohr, and C. Bauckhage, “Evaluation of interest point detectors,” International Journal of Computer Vision, vol. 37, no. 2, pp. 151–172, 2000. [216] S. Se, T. Barfoot, and P. Jasiobedzki, “Visual motion estimation and terrain modeling for planetary rovers,” in Proceedings of the International Symposium on Artiﬁcial Intelligence for Robotics and Automation in Space, 2005.

[217] N. Sebe, T. Gevers, J. van de Weijer, and S. Dijkstra, “Corner detectors for aﬃne invariant salient regions: Is color important,” in Proceedings of International Conference on Image and Video Retrieval, pp. 61–71, 2006.

[218] N. Sebe, Q. Tian, E. Loupias, M. Lew, and T. Huang, “Evaluation of salient point techniques,” Image and Vision Computing, vol. 21, no. 13–14, pp. 1087– 1095, 2003.

[219] R. Sedgewick, Algorithms. Addison–Wesley, Second Edition, 1988.

[220] E. Seemann, B. Leibe, K. Mikolajczyk, and B. Schiele, “An evaluation of local shape-based features for pedestrian detection,” in Proceedings of the British Machine Vision Conference, pp. 11–20, 2005.

[221] T. Serre, L. Wolf, S. Bileschi, M. Riesenhuber, and T. Poggio, “Robust object recognition with cortex-like mechanisms,” IEEE Transactions on Pattern Analysis and Machine Intelligence, vol. 29, no. 3, pp. 411–426, 2007.

[222] T. Serre, L. Wolf, and T. Poggio, “Object recognition with features inspired by visual cortex,” in Proceedings of the Conference on Computer Vision and Pattern Recognition, 2005.

[223] A. Sha’ashua and S. Ullman, “Structural saliency: The detection of globally salient structures using a locally connected network,” in Proceedings of the International Conference on Computer Vision, pp. 321–327, 1988.

[224] M. A. Shah and R. Jain, “Detecting time-varying corners,” Computer Vision, Graphics and Image Processing, vol. 28, pp. 345–355, 1984.

[225] E. Sharon, A. Brandt, and R. Basri, “Segmentation and boundary detection using multiscale intensity measurements,” in Proceedings of the Conference on Computer Vision and Pattern Recognition, pp. 469–476, 2001.

[226] F.ShenandH.Wang,“CornerdetectionbasedonmodiﬁedHoughtransform,” Pattern Recognition Letters, vol. 23, no. 8, pp. 1039–1049, 2002.

[227] J. Shi and J. Malik, “Normalized cuts and image segmentation,” IEEE Transactions on Pattern Analysis and Machine Intelligence, vol. 22, no. 8, pp. 888– 905, 2000.

[228] J. Shi and C. Tomasi, “Good features to track,” in Proceedings of the Conference on Computer Vision and Pattern Recognition, pp. 593–600, 1994. [229] A. Singh and M. Shneier, “Gray-level corner detection a generalization and a robust real time implementation,” in Proceedings of the Computer Vision Graphics Image Processing, vol. 51, pp. 54–69, 1990.

[230] S. N. Sinha, J. M. Frahm, M. Pollefeys, and Y. Genc, “GPU-based video feature tracking and matching,” in EDGE, Workshop on Edge Computing Using New Commodity Architectures, 2006.

[231] J. Sivic and A. Zisserman, “Video google: A text retrieval approach to object matching in videos,” in Proceedings of the International Conference on Computer Vision, pp. 1470–1478, 2003.

[232] S. M. Smith and J. M. Brady, “SUSAN — A new approach to low level image processing,” International Journal of Computer Vision, vol. 23, no. 34, pp. 45–78, 1997.

[233] K. Sohn, J. H. Kim, and W. E. Alexander, “A mean ﬁeld annealing approach to robust corner detection,” IEEE Transactions on Systems Man Cybernetics Part B, vol. 28, pp. 82–90, 1998.

[234] J. Sporring, M. Nielsen, L. Florack, and P. Johansen, Gaussian Scale-Space Theory. Springer-Verlag, 1997.

[235] M. Stark and B. Schiele, “How good are local features for classes of geometric objects,” in Proceedings of the International Conference on Computer Vision, 2007.

[236] B. Super and W. Klarquist, “Patch-based stereo in a general binocular viewing geometry,” IEEE Transactions on Pattern Analysis and Machine Intelligence, vol. 19, no. 3, pp. 247–252, 1997.

[237] M. Swain and D. Ballard, “Color indexing,” International Journal in Computer Vision, vol. 7, no. 1, pp. 11–32, 1991.

[238] C.-H. Teh and R. T. Chin, “On the detection of dominant points on digital curves,” IEEE Transactions on Pattern Analysis and Machine Intelligence, vol. 11, pp. 859–872, 1989.

[239] P.TissainayagamandD.Suter,“Assessingtheperformanceofcornerdetectors for point feature tracking applications,” Image and Vision Computing, vol. 22, no. 8, pp. 663–679, 2004.

[240] M. Trajkovic and M. Hedley, “Fast corner detection,” Image and Vision Computing, vol. 16, no. 2, pp. 75–87, 1998.

[241] A. M. Treisman, “Features and objects: The fourteenth Berlett memorial lecture,” Journal of Experimantal Psychology, vol. 40A, pp. 201–237, 1988.

[242] W. Triggs, “Detecting keypoints with stable position, orientation and scale under illumination changes,” in Proceedings of the European Conference on Computer Vision, vol. 4, pp. 100–113, 2004.

[243] L. Trujillo and G. Olague, “Synthesis of interest point detectors through genetic programming,” Genetic and Evolutionary Computation, pp. 887–894, 2006.

[244] D.M.Tsai,“Boundary-basedcornerdetectionusingneuralnetworks,”Pattern Recognition, vol. 30, pp. 85–97, 1997.

[245] M. A. Turk and A. P. Pentland, “Eigenfaces for face recognition,” in Proceedings of the Conference on Computer Vision and Pattern Recognition, pp. 586– 591, 1991.

[246] T. Tuytelaars and C. Schmid, “Vector quantizing feature space with a regular lattice,” in Proceedings of the International Conference on Computer Vision, 2007.

[247] T. Tuytelaars and L. Van Gool, “Content-based image retrieval based on local aﬃnely invariant regions,” in International Conference on Visual Information Systems, pp. 493–500, 1999.

[248] T. Tuytelaars and L. Van Gool, “Wide baseline stereo matching based on local, aﬃnely invariant regions,” in Proceedings of the British Machine Vision Conference, pp. 412–425, 2000.

[249] T. Tuytelaars and L. Van Gool, “Matching widely separated views based on aﬃne invariant regions,” International Journal of Computer Vision, vol. 1, no. 59, pp. 61–85, 2004.

[250] J. van de Weijer, T. Gevers, and A. D. Bagdanov, “Boosting color saliency in image feature detection,” IEEE Transactions on Pattern Analysis and Machine Intelligence, vol. 28, no. 1, pp. 150–156, 2006.

[251] A. Vedaldi and S. Soatto, “Features for recognition: Viewpoint invariance for non-planar scenes,” in Proceedings of the International Conference on Computer Vision, pp. 1474–1481, 2005.

[252] P. Viola and M. Jones, “Rapid object detection using a boosted cascade of simple features,” in Proceedings of the Conference on Computer Vision and Pattern Recognition, vol. 1, pp. 511–518, 2001.

[253] K. N. Walker, T. F. Cootes, and C. J. Taylor, “Locating salient object features,” in Proceedings of the British Machine Vision Conference, 1998.

[254] H. Wang and M. Brady, “Real-time corner detection algorithm for motion estimation,” Image and Vision Computing, vol. 13, no. 9, pp. 695–703, 1995.

[255] R. J. Watt, “Scanning from coarse to ﬁne spatial scales in the human visual system after the onset of a stimulus,” Journal of Optical Society of America, vol. 4, no. 10, pp. 2006–2021, 1987.

[256] S. Winder and M. Brown, “Learning local image descriptors,” International Conference on Computer Vision and Pattern Recognition, 2007.

[257] J. Winn, A. Criminisi, and T. Minka, “Object categorization by learned universal visual dictionary,” in Proceedings of the International Conference on Computer Vision, vol. 2, pp. 1800–1807, 2005.

[258] A. P. Witkin, “Scale-space ﬁltering,” in Proceedings of the International Joint Conference on Artiﬁcial Intelligence, pp. 1019–1023, 1983.

[259] M. Worring and A. W. M. Smeulders, “Digital curvature estimation,” CVGIP: Image Understanding, vol. 58, no. 3, pp. 366–382, 1993.

[260] R. P. Wurtz and T. Lourens, “Corner detection in color images through a multiscale combination of end-stopped cortical cells,” Image and Vision Computing, vol. 18, no. 6–7, pp. 531–541, 2000.

[261] X. Zhang, R. Haralick, and V. Ramesh, “Corner detection using the map technique,” in Proceedings of the International Conference on Pattern Recognition, vol. 1, pp. 549–552, 1994.

[262] X. Zhang and D. Zhao, “A morphological algorithm for detecting dominant points on digital curves,” SPIE Proceedings, Nonlinear Image Processing 2424, pp. 372–383, 1995.

[263] Z. Zheng, H. Wang, and E. Teoh, “Analysis of gray level corner detection,” Pattern Recognition Letters, vol. 20, pp. 149–162, 1999.

[264] P. Zhu and P. M. Chirlian, “On critical point detection of digital shapes,” IEEE Transactions on Pattern Analysis and Machine Intelligence, vol. 17, no. 8, pp. 737–748, 1995.

[265] M. Zuliani, C. Kenney, and B. S. Manjunath, “A mathematical comparison of point detectors,” in Proceedings of the Computer Vision and Pattern Recognition Workshop, p. 172, 2004.

[266] O. A. Zuniga and R. Haralick, “Corner detection using the facet model,” in Proceedings of the Conference on Computer Vision and Pattern Recognition, pp. 30–37, 1983.

posted on 2019-09-11 23:00 Alliswell_WP 阅读(330) 评论(0) 编辑收藏举报

刷新页面返回顶部

Image Processing and Computer Vision_Review：Local Invariant Feature Detectors: A Survey——2007.11

导航

公告