Image Processing and Computer Vision_Review：A Performance Evaluation of Local Descriptors——2005.08

翻译

本地描述符的性能评估——http://tongtianta.site/paper/56756

 

摘要 - 在本文中，我们比较了为局部感兴趣区域计算的描述符的性能，例如，由Harris-Affine检测器[32]提取。在文献中已经提出了许多不同的描述符。目前还不清楚哪些描述符更合适以及它们的性能如何取决于兴趣区域检测器。描述符应该是独特的，同时对于观察条件的变化以及检测器的误差是稳健的。我们的评估使用关于精度的标准调用，并且针对不同的图像变换执行。我们比较形状上下文[3]，可控滤波器[12]，PCA-SIFT [19]，微分不变量[20]，自旋图像[21]，SIFT [26]，复数滤波器[37]，矩不变量[43]，和不同类型的兴趣区域的互相关。我们还提出了SIFT描述符的扩展，并表明它优于原始方法。此外，我们观察到描述符的排名主要独立于兴趣区域检测器，并且基于SIFT的描述符表现最佳。力矩和可控滤波器在低维描述符中表现出最佳性能。
索引 - 局部描述符，兴趣点，兴趣区域，不变性，匹配，识别。

 

1简介
已经证明，针对感兴趣区域计算的局部光度描述符在诸如宽基线匹配[37]，[42]，物体识别[10]，[25]，纹理识别[21]，图像检索[29]等应用中非常成功， [38]，机器人定位[40]，视频数据挖掘[41]，建筑全景图[4]，以及对象类别的识别[8]，[9]，[22]，[35]。它们独特，对遮挡具有鲁棒性，并且不需要分割。最近的工作集中在使这些描述符对图像变换不变。该想法是检测与一类变换协变的图像区域，然后将其用作支持区域以计算不变描述符。给定不变区域检测器，剩下的问题是哪个描述符最适合表征区域以及描述符的选择是否取决于区域检测器。存在大量可能的描述符和相关的距离度量，其强调不同的图像属性，例如像素强度，颜色，纹理，边缘等。在这项工作中，我们关注于在灰度值图像上计算的描述符。

描述符的评估是在匹配和识别在不同观看条件下观察到的相同场景或对象的上下文中执行的。我们选择了许多描述符，这些描述符之前在这样的上下文中表现出良好的性能，并使用相同的评估方案和相同的测试数据进行比较。评估标准是召回精度，即两个图像之间的正确和错误匹配的数量。另一种可能的评估标准是从数据库中检索图像的背景下的ROC（接收器操作特性）[6]，[31]。检测率等同于召回，但是针对图像数据库而不是单个图像对计算误报率。因此难以预测一对相似图像的错误匹配的实际数量。
局部特征也成功用于对象类别识别和分类。在此上下文中描述符的比较需要不同的评估设置。目前还不清楚如何为对象类别选择代表性的图像集以及如何准备地面实况，因为没有与类别内的图像相关的线性变换。一种可能的解决方案是手动选择几个相应的点并应用松散的约束来验证正确的匹配，如[18]中所提出的。

在本文中，对不同的描述符，不同的兴趣区域和不同的匹配方法进行了比较。与我们以前的工作[31]相比，本文进行了更详尽的评估并引入了新的描述符。比较中添加了几个描述符和检测器，数据集包含更多种类的场景类型和转换。我们修改了评估标准，现在使用图像对的召回精度。最高描述符的排名与基于ROC的评估相同[31]。此外，我们的新描述符，渐变位置和方向直方图（GLOH），它是SIFT描述符的扩展，显示出优于SIFT以及其他描述符。

1.1相关工作
绩效评估在计算机视觉中越来越重要[7]。在匹配和识别的背景下，一些作者已经评估了兴趣点检测器[14]，[30]，[33]，[39]。性能通过可重复率来测量，即两个图像中同时存在的点的百分比。两个图像之间的可重复率越高，可能匹配的点越多，匹配和识别结果越好。

在匹配和识别的背景下，对局部描述符的评估工作很少。 Carneiro和Jepson [6]使用ROC（接收器操作特性）评估点描述符的性能。他们表明，他们的基于阶段的描述符比差分不变量更好。在它们的比较中，Harris检测器检测兴趣点并且人工生成图像变换。最近，Ke和Sukthankar [19]开发了一个类似于SIFT描述符的描述符。它将主成分分析（PCA）应用于归一化图像梯度补丁，并且在人工生成的数据上比SIFT描述符执行得更好。标准召回精度和图像对用于比较描述符。在纹理分类的上下文中也评估了局部描述符（也称为过滤器）。 Randen和Husoy [36]比较了一种纹理分类算法的不同滤波器。本文评估的滤波器是Laws掩模，Gabor滤波器，小波变换，DCT，本征滤波器，线性预测器和优化的有限脉冲响应滤波器。没有一种方法被认为是最好的。分类错误取决于纹理类型和描述符的维度。 Gabor滤波器在大多数情况下优于其他滤波器。 Varma和Zisserman [44]也比较了不同的纹理分类滤波器，并表明MRF比基于高斯的滤波器组表现更好。 Lazebnik等人。 [21]提出了一种称为“自旋图像”的新的不变描述符，并在纹理分类的上下文中将其与Gabor滤波器进行比较。他们表明，基于区域的旋转图像优于基于点的Gabor滤波器。但是，纹理描述符和纹理分类的结果不能直接转换为区域描述符。这些区域通常包含没有重复模式的单一结构，并且在此上下文中不能使用纹理描述符中经常探索的统计依赖性。

1.2概述
在第2节中，我们介绍了本地描述符的最新技术。第3节描述了我们的比较中使用的检测器和描述符的实现细节以及我们的评估标准和数据集。在第4节中，我们介绍了实验结果。最后，我们将讨论第5节中的结果。

2描述符
已经开发了许多用于描述局部图像区域的不同技术。最简单的描述符是图像像素的矢量。然后可以使用互相关来计算两个描述符之间的相似性得分。然而，这种描述的高维度导致用于识别的高计算复杂度。因此，该技术主要用于寻找两个图像之间的对应关系。请注意，可以对区域进行二次采样以减小尺寸。最近，Ke和Sukthankar [19]提出使用图像梯度补丁并应用PCA来减小描述符的大小。
2.1基于分布的描述符
这些技术使用直方图来表示外观或形状的不同特征。简单描述符是由直方图表示的像素强度的分布。 Johnson和Hebert [17]在范围数据的背景下引入了更具表现力的表示。它们的表示（自旋图像）是3D兴趣点附近的点位置的直方图。这个描述符最近适用于图像[21]。直方图的两个维度是距中心点和强度值的距离。

Zabih和Woodfill [45]已经开发出一种对光照变化具有鲁棒性的方法。它依赖于排序的直方图和像素强度之间的相互关系，其比原始像素强度更稳健。几个相邻像素的强度之间的二元关系由二进制串编码，并且所有可能组合的分布由直方图表示。该描述符适用于纹理表示，但是需要大量维度来构建可靠的描述符[34]。
Lowe [25]提出了一种尺度不变特征变换（SIFT），它结合了尺度不变区域检测器和基于检测区域中梯度分布的描述符。描述符由梯度位置和方向的3D直方图表示;参见图1的说明。对位置和方向箱的贡献由梯度幅度加权。梯度位置和方向的量化使得描述符对于小的几何失真和区域检测中的小误差是鲁棒的。几何直方图[1]和形状上下文[3]实现了相同的思想，与SIFT描述符非常相似。两种方法都计算描述区域中边缘分布的直方图。这些描述符被成功地用于例如边缘是可靠特征的图形的形状识别。

2.2空间频率
技术许多技术描述图像的频率内容。傅里叶变换将图像内容分解为基函数。然而，在这种表示中，点之间的空间关系不明确，基函数是无穷大的;因此，很难适应当地的方法。 Gabor变换[13]克服了这些问题，但需要大量的Gabor滤波器来捕捉频率和方向的微小变化。 Gabor滤波器和小波[27]经常在纹理分类的背景下进行探索。

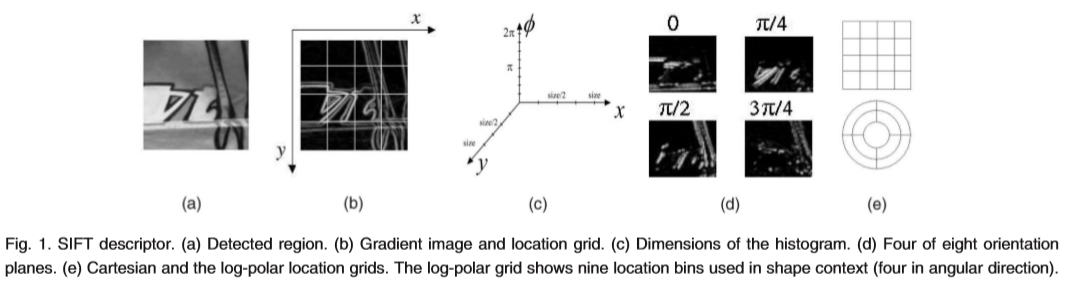
图1. SIFT描述符。 （a）检测区域。 （b）梯度图像和位置网格。 （c）直方图的尺寸。 （d）八个定向平面中的四个。 （e）笛卡尔坐标和对数极坐标定位网格。对数极坐标网格显示了在形状上下文中使用的九个位置区间（角度方向上有四个）。

 

图2.基于导数的滤波器。 （a）高斯导数至四阶。 （b）复杂滤波器，最多六阶。请注意，为清晰起见，显示的滤波器未按高斯加权。

 

2.3差分描述符
计算到给定顺序的一组图像导数近似于点邻域。 Koenderink和van Doorn [20]研究了局部衍生物（局部喷射）的性质。 Florack等人。 [11]推导出微分不变量，它结合局部射流的成分来获得旋转不变性。 Freeman和Adelson [12]开发了可操纵的过滤器，它可以根据当地喷气机的组件在特定方向上引导衍生物。在梯度方向上的转向导数使它们对旋转不变。通过与高斯导数的卷积获得对导数的稳定估计。图2a显示高达4阶的高斯导数。
Baumberg [2]和Schaffalitzky和Zisserman [37]提出使用从族K（x，y，s）-f（x，y）exp（is）导出的复数滤波器，其中s是方向。对于函数f（x，y），Baumberg使用高斯导数，Schaffalitzky和Zisserman应用多项式（参见第3.2节和图2b）。这些滤波器与滤波器响应域中的线性坐标变化的高斯导数不同。

2.4其他技术
Van Gool等人引入了广义矩不变量。 [43]描述图像数据的多光谱性质。不变量组合由阶数为p + q和度数a的Ma定义的中心矩。这些时刻表征了区域O中的形状和强度分布。它们是独立的，可以根据任何顺序和程度轻松计算。然而，高阶和高度的时刻对小的几何和光度畸变敏感。计算不变量可减少维数。因此，这些描述符更适合于彩色图像，其中可以为每个颜色通道和通道之间计算不变量。

 

3实验设置
在下文中，我们首先描述在我们的比较中使用的区域检测器和计算描述符所需的区域归一化。然后，我们为评估的描述符提供实现细节。最后，我们讨论评估标准和测试中使用的图像数据。

3.1支持区域
最近提出了许多尺度和仿射不变区域检测器。 Lindeberg [23]开发了一种尺度变化的“斑点”探测器，其中“斑点”由尺度空间中的最大归一化拉普拉斯算子定义。 Lowe [25]用高斯差分（DoG）滤波器逼近拉普拉斯算子，并且还检测尺度空间中的局部极值。 Lindeberg和Ga˚rding[24]使用基于第二矩矩阵的仿射适应过程使斑点检测器仿射不变。 Mikolajczyk和Schmid [29]，[30]使用多尺度版本的Harris兴趣点检测器来定位空间中的兴趣点，然后采用Lindeberg的方案进行尺度选择和仿射适应。 Baumberg [2]以及Schaffalitzky和Zisserman [37]也探讨了类似的想法。 Tuytelaars和Van Gool [42]构造了两种类型的仿射不变区域，一种基于感兴趣点和边缘的组合，另一种基于图像强度。马塔斯等人。 [28]介绍了用分水岭分割算法提取的极大稳定极值区域。卡迪尔等人。 [18]测量为椭圆区域计算的像素强度直方图的熵，以找到仿射变换空间中的局部最大值。在[33]中可以找到最先进的仿射区域探测器的比较。

3.1.1区域探测器
检测器提供用于计算描述符的区域。如果没有另外说明，则检测标度确定区域的大小。在这次评估中，我们使用了五个探测器：
哈里斯点[15]对旋转是不变的。支撑区域是以兴趣点为中心的41×41像素的固定大小邻域。
Harris-Laplace区域[29]对旋转和尺度变化不变。这些点由尺度自适应Harris函数检测，并由拉普拉斯高斯算子在尺度空间中选择。哈里斯 - 拉普拉斯检测到角状结构。

Hessian-Laplace区域[25]，[32]对旋转和尺度变化是不变的。点在Hessian行列式的局部最大值处的空间中定位，并且在拉普拉斯高斯的局部最大值处按比例定位。该探测器类似于DoG方法[26]，其在高斯差的局部尺度 - 空间最大值处定位点。两种方法都检测到类似的类似blob的结构。然而，Hessian-Laplace在尺度空间中获得了更高的定位精度，因为DoG也响应边缘并且在这种情况下检测是不稳定的。比例选择精度也高于Harris-Laplace检测器的情况。拉普拉斯尺度选择充当匹配滤波器，并且对于类似blob的结构比在角上更好地工作，因为拉普拉斯内核的形状适合于斑点。检测器的准确性会影响描述符性能。
Harris-Affine区域[32]对仿射图像变换是不变的。通过Harris-Laplace检测器估计定位和比例。仿射邻域由基于第二矩矩阵的仿射适应过程确定。
Hessian-Affine区域[33]对于仿射图像变换是不变的。通过Hessian-Laplace检测器估计定位和尺度，并且仿射邻域由仿射适应过程确定。

注意Harris-Affine与Harris-Laplace的不同之处在于仿射适应，它适用于Harris-Laplace区域。在这个比较中，我们使用相同的区域，但对于Harris-Laplace，区域形状是圆形的。基于Hessian的探测器也是如此。因此，对于仿射和尺度不变的检测器，区域的数量是相同的。 [32]中描述了这些探测器的实现细节以及默认阈值。根据内容，检测到的区域的数量从每个图像200到3,000变化。
3.1.2区域规范化

探测器提供不同尺寸的圆形或椭圆形区域，这取决于检测尺度。给定检测到的区域，可以通过比例或仿射协变构造来改变其大小或形状。因此，我们可以修改有助于描述符计算的像素集。通常，较大的区域包含更多的信号变化。 Hessian-Affine和Hessian-Laplace主要检测斑点状结构，信号变化位于斑点边界上。为了将这些信号变化包括在描述中，测量区域是检测区域的三倍。该因子用于所有比例和仿射检测器。将所有区域映射到恒定半径的圆形区域以获得尺度和仿射不变性。归一化区域的大小不应太小，以便在足够的分辨率下表示局部结构。在实验中，这个大小任意设置为41个像素。在[19]中使用了类似的贴片尺寸。
在大小归一化之前平滑大于归一化大小的区域。平滑高斯核的参数由比率测量/归一化区域大小给出。旋转图像，微分不变量和复数滤波器对于旋转是不变的。为了获得其他描述符的旋转不变性，归一化区域在主要梯度方向的方向上旋转，其在区域中心的小邻域中计算。为了估计主导方向，我们建立梯度角度的直方图直方图，并根据[25]中的建议选择与最大直方图区间相对应的方向。

照明变化可以通过像素强度的仿射变换aI对比来建模。为了补偿这种仿射照明变化，使用该区域内像素强度的平均值和标准偏差对图像块进行归一化。如果没有另外说明，则使用该方法对用于描述符评估的区域进行标准化。基于导数的描述符（可操纵滤波器，微分不变量）也可以通过计算照明不变量来归一化。通过微分运算消除偏移b。通过将高阶导数除以提高到适当功率的梯度幅度来获得具有因子a的线性缩放的不变性。对于矩和复数滤波器，可以进行类似的归一化，但这里没有实现。
3.2描述符

在下文中，我们将介绍实验评估中使用的描述符的实现细节。我们使用10种不同的描述符：SIFT [25]，梯度位置和方向直方图（GLOH），形状上下文[3]，PCA-SIFT [19]，自旋图像[21]，可控滤波器[12]，微分不变量[20] ，复数滤波器[37]，矩不变量[43]，以及采样像素值的互相关。梯度位置和方向直方图（GLOH）是一种新的描述符，它通过改变位置网格和使用PCA来减小尺寸来扩展SIFT。

使用由Lowe [25]提供的代码计算归一化图像块的SIFT描述符。描述符是梯度位置和方向的3D直方图，其中位置被量化为4 4位置网格，并且梯度角被量化为8个方向。得到的描述符具有维度128.图1示出了该方法。每个定向平面表示对应于给定方向的梯度大小。为了获得光照不变性，描述符通过平方分量之和的平方根来归一化。

梯度定位直方图（GLOH）是SIFT描述符的扩展，旨在增强其鲁棒性和独特性。我们计算了对数极坐标位置网格的SIFT描述符，其中径向有三个箱（半径设置为6,11和15），角度方向为8个，这导致17个位置箱。注意，中央箱不在角度方向上划分。梯度方向在16个区间中量化。这给出了272个bin直方图。使用PCA可以减小此描述符的大小。 PCA的协方差矩阵估计是从各种图像中收集的47,000个图像补丁（参见第3.3.1节）。 128个最大的特征向量用于描述。 Shape上下文类似于SIFT描述符，但基于边缘。
形状上下文是边缘点位置和方向的3D直方图。边缘由Canny [5]探测器提取。位置被量化为对数极坐标系的九个区间，如图1e所示，半径设置为6,11和15，并且方向被量化为四个区间（水平，垂直和两个对角线）。因此，我们获得了36维描述符。在我们的实验中，我们用梯度幅度加权直方图的点贡献。已经证明，与[3]中提出的所有边缘点使用相同的权重相比，这可以得到更好的结果。请注意，原始形状上下文仅针对边缘点位置而非针对方向计算。
PCA-SIFT描述符是在支持区域内计算的x和y方向上的图像梯度的矢量。梯度区域在39 39个位置处被采样，因此，向量的大小为3,042。使用PCA将尺寸减小到36。

旋转图像是量化像素位置和强度值的直方图。标准化补丁的强度被量化为10个区间。针对以该区域为中心的五个环中的每个环计算10 bin归一化直方图。自旋描述符的维数是50。
可控滤波器和微分不变量使用通过卷积计算的导数和sigma = 6.7的高斯导数用于尺寸为41的图像块。如[12]中提出的改变导数的方向给出了计算旋转图像块上的局部射流的等效结果。我们使用第二种方法。导数计算到四阶，即描述符具有维数14.图2a显示了14个导数中的8个;通过旋转90度获得剩余的衍生物。差分不变量计算到三阶（维度8）。

我们比较了可控滤波器和按相同顺序计算的微分不变量（参见4.1.3节）。复数滤波器由以下等式导出：K（x，y）。原始实现[37]已用于生成内核。针对半径为1的单位磁盘计算内核，并在41 * 41位置进行采样。我们使用由m + n <6定义的15个滤波器（交换m和n只给出复共轭滤波器）; m = n = 0的滤波器的响应是该区域的平均强度。图2b显示了15个滤波器中的8个。轮换会改变阶段，但不会改变响应的幅度;因此，我们使用每个复数滤波器响应的模数。
矩不变量计算到二阶和二阶。对于具有Ma的图像块的导数计算矩，其中p + q是阶数，a是度，并且Id是方向d上的图像梯度。衍生物在x和y方向上计算。这导致20维描述符（没有Ma的2 * 10）。注意，最初，不变矩是在彩色图像上计算的[43]。
互相关。为了获得该描述符，对该区域进行平滑和均匀采样。为了限制描述符维度，我们在9 * 9像素位置进行采样。用互相关测量两个描述符之间的相似性。

距离测量。描述符之间的相似性用可控滤波器的马哈拉诺比斯距离，微分不变量，矩不变量和复数滤波器计算。我们为描述符/检测器的每个组合估计一个协方差矩阵C;所有实验都使用相同的矩阵。在与测试数据不同的图像上估计矩阵。我们使用了21个平面场景的图像序列，在我们评估描述符的所有变换下查看。存在大约15,000个相应区域的链，每个链具有至少三个区域。使用独立估计的单应性来建立对应链（参见3.3.1节关于单应性估计的细节）。然后，我们计算每个链的各个协方差矩阵的平均值。我们还用对角协方差矩阵进行了实验，得到了几乎相同的结果。欧几里德距离用于比较基于直方图的描述符，即SIFT，GLOH，PCA-SIFT，形状上下文和旋转图像。注意，描述符归一化的协方差矩阵的估计不同于用于PCA的协方差矩阵的估计。对于PCA，从大约47,000个描述符计算一个协方差矩阵。
3.3绩效评估

3.3.1数据集
我们使用不同的几何和光度变换以及不同的场景类型来评估真实图像上的描述符。图3显示了用于评估的数据集1的示例图像。评估六个图像变换：旋转（图3a和3b）;规模变化（图3c和3d）;观点变化（图3e和3f）;图像模糊（图3g和3h）; JPEG压缩（图3i）;和照明（图3j）。在旋转，比例变化，视点变化和模糊的情况下，我们使用两种不同的场景类型。一种场景类型包含结构化场景，即具有独特边缘边界的均匀区域（例如，涂鸦，建筑物），而另一种场景类型包含不同形式的重复纹理。这使我们可以分别分析图像变换和场景类型的影响。

通过使相机围绕其光轴在30度和45度的范围内旋转来获得图像旋转。通过分别改变相机变焦和聚焦来获取比例变化和模糊序列。比例变化范围为2-2.5。在视点改变序列的情况下，摄像机位置从前平行视图变为具有大约50-60度的显着缩短的视图。通过改变相机光圈来引入光变化。 JPEG序列使用标准xv图像浏览器生成，图像质量参数设置为5％。图像是平面场景或摄像机位置在采集期间是固定的。因此，图像总是通过单应性（平面投影变换）相关。基本事实单应性分两步计算。首先，使用手动选择的对应关系计算单应性的近似值。然后用该单应性扭曲变换后的图像，使其与参考图像大致对齐。其次，使用稳健的小基线单应性估计算法来计算参考图像和变形图像之间的精确残差单应性，具有自动检测和匹配的兴趣点[16]。近似和残差单应性的组成导致图像之间的精确单应性。

在第4节中，我们显示了图3中图像对的结果。这些图像之间的转换足以在检测到的区域中引入一些噪声。然而，找到了许多对应关系并且匹配结果是稳定的。通常，对于小图像变换，描述符性能较高，但排名保持不变。大变换的对应区域很少，并且召回精度曲线不平滑。
使用与测试数据不同的数据集来估计PCA和描述符归一化的协方差矩阵。在这两种情况下，我们使用了21个不同平面场景的图像序列，这些图像序列在我们评估描述符的所有变换下查看。
3.3.2评估标准

我们使用类似于[19]中提出的标准。它基于正确匹配的数量和为图像对获得的错误匹配的数量。如果它们的描述符DA和DB之间的距离低于阈值t，则匹配两个区域A和B.将来自参考图像的每个描述符与来自变换的一个描述符的每个描述符进行比较，并且我们计算正确匹配的数量以及错误匹配的数量。改变t的值以获得曲线。结果以召回与1精度呈现。召回是相对于同一场景的两个图像之间的对应区域的数量的正确匹配区域的数量：

 

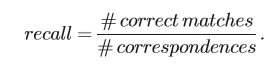
正确匹配和对应的数量由重叠误差[30]确定。重叠误差测量区域在变换下的对应程度，这里是单应性。它由区域的交叉和并集的比率来定义：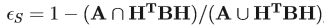

其中A和B是区域，H是图像之间的单应性（参见第3.3.1节）。给定单应性和定义区域的矩阵，误差以数字计算。我们的方法计算联合中的像素数和区域的交集。细节可以在[33]中找到。如果两个相应区域覆盖的图像区域中的误差小于区域并集的50％，即S <0：5，则我们假设匹配是正确的。计算用于计算描述符的测量区域的重叠。通常，很少有具有较大误差的相应区域被正确匹配，并且这些匹配不用于计算召回。对应的数量（可能的正确匹配）用相同的标准确定。

相对于匹配总数的错误匹配数由1精度表示：

 

给定回忆，1精度和相应区域的数量，正确匹配的数量，可以通过＃correspondences.recall和错误匹配的数量来确定。

 

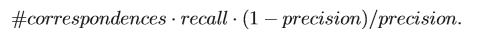
例如，在用于生成图4a的图像之间存在3,708个对应区域。对于GLOH曲线上的点，调用0.3和1精度为0.6，正确匹配的数量为3.708 * 0.3 = 1.112，错误匹配的数量为3.708 * 0.3 * 0.6 /（1-0.6）= 1.668 。请注意，召回和1精度是独立的术语。召回是根据相应区域的数量和相对于总匹配数的1精度计算的。

 

在我们开始评估之前，我们讨论图形的解释和可能的曲线形状。对于任何精度，完美的描述符将使召回等于1。在实践中，由于通过图像变换和区域检测引入的噪声增加了相似描述符之间的距离，因此增加距离阈值的召回增加。水平曲线表示以高精度获得调用并且受到场景特异性的限制，即，检测到的结构彼此非常相似，并且描述符不能区分它们。不增加召回的另一个可能原因是剩余的相应区域彼此非常不同（部分重叠接近50％），因此描述符是不同的。缓慢增加的曲线表明描述符受到图像劣化（视点变化，模糊，噪声等）的影响。如果对应于不同描述符的曲线相距很远或具有不同的斜率，则描述符的区别性和鲁棒性对于所研究的图像变换或场景类型是不同的。

 

图3.数据集。用于评估的图像的示例：（a）和（b）旋转，（c）和（d）变焦+旋转，（e）和（f）视点改变，（g）和（h）图像模糊，（i） ）JPEG压缩，以及（j）光变化。

4实验结果
在本节中，我们将介绍和讨论评估的实验结果。比较仿射变换，比例变化，旋转，模糊，jpeg压缩和照明变化的性能。在仿射变换的情况下，我们还检查不同的匹配策略，重叠误差的影响和描述符的维度。
4.1仿射变换
在本节中，我们评估大约50度的视点变化的性能。这引入了透视变换，其可以局部地通过仿射变换来近似。这是本文评估的最具挑战性的转换。请注意，测试图像中也存在一些比例和亮度变化，请参见图3和图4。 3e和3f。在下文中，我们首先研究不同的匹配方法。其次，我们研究了重叠误差对匹配结果的影响。第三，我们评估不同描述符维度的性能。第四，我们比较不同区域探测器和场景类型的描述符性能。

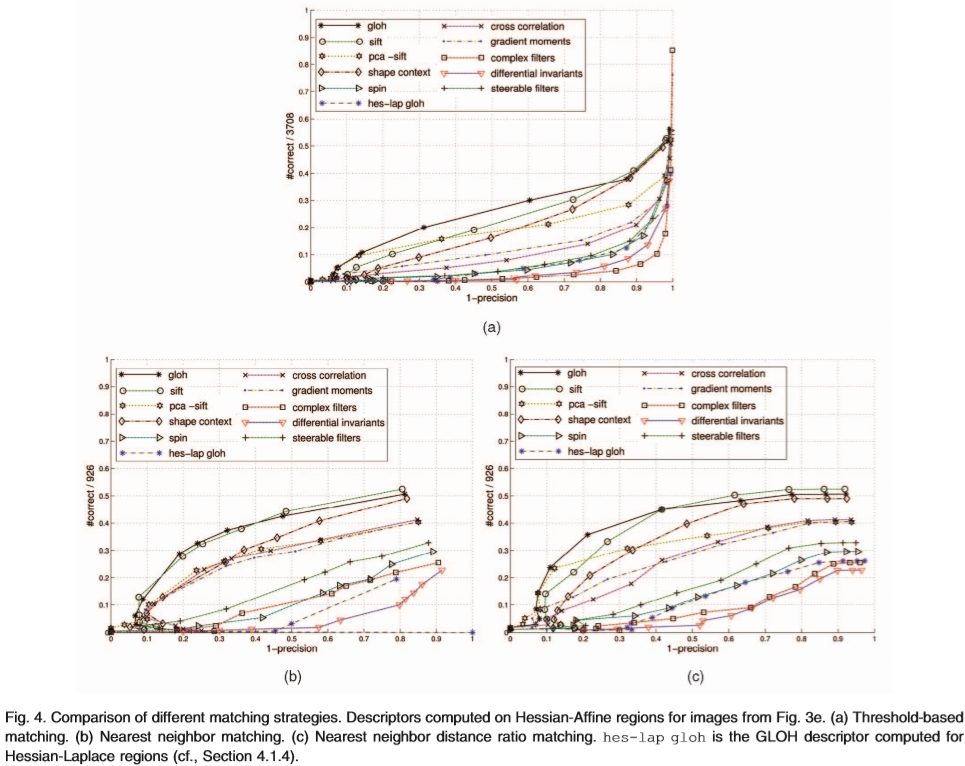
图4.不同匹配策略的比较。对于来自图3e的图像，在Hessian-Affine区域上计算描述符。 （a）基于阈值的匹配。 （b）最近邻匹配。 （c）最近邻距离比匹配。 hes-lap gloh是为Hessian-Laplace区域计算的GLOH描述符（参见4.1.4节）。

4.1.1匹配策略
匹配的定义取决于匹配策略。我们比较其中三个。在基于阈值的匹配的情况下，如果两个区域的描述符之间的距离低于阈值，则匹配两个区域。描述符可以有几个匹配，其中几个可能是正确的。在最近邻匹配的情况下，如果描述符DB是DA的最近邻居并且它们之间的距离低于a，则匹配两个区域A和B.阈。使用这种方法，描述符只有一个匹配。第三匹配策略类似于最近邻匹配，除了阈值处理应用于第一和第二最近邻居之间的距离比。因此，如果|| DA -DB ||，则匹配区域= || DA -DC || <t，其中DB是第一个，DC是DA的第二个最近邻居。所有匹配策略将参考图像的每个描述符与变换图像的每个描述符进行比较。
图图4a，4b和4c显示了三种匹配策略的结果。描述符是在Hessian-Affine区域上计算的。对于所有匹配策略，描述符的排名是类似的。最近邻匹配（NN）和基于最近邻距离比（NNDR）的匹配之间存在一些小的变化。在图4c中，其显示了NNDR的结果，SIFT明显优于PCA-SIFT，而GLOH获得与SIFT类似的分数。互相关和复数滤波器获得的分数略好于基于阈值和最近邻匹配。时刻在NNDR匹配中执行以及互相关和PCA-SIFT（参见图4c）。

基于最近邻居的匹配（参见图4b和4c）的精度高于基于阈值的方法（参见图4a）。这是因为最近邻居大部分是正确的，尽管类似描述符之间的距离由于图像变换而显着变化。最近邻匹配仅选择低于阈值的最佳匹配并拒绝所有其他匹配;因此，错误匹配较少，精度较高。基于最近邻距离比的匹配是类似的，但另外惩罚具有许多相似匹配的描述符，即，到最近邻居的距离与到其他描述符的距离相当。这进一步提高了精度。基于邻近的最近技术可以在匹配的上下文中使用;但是，在大型数据库中搜索描述符时，很难应用它们。然后，描述符之间的距离是主要的相似性标准。基于距离阈值的匹配结果反映了空间中描述符的分布;因此，我们将这种方法用于我们的实验。

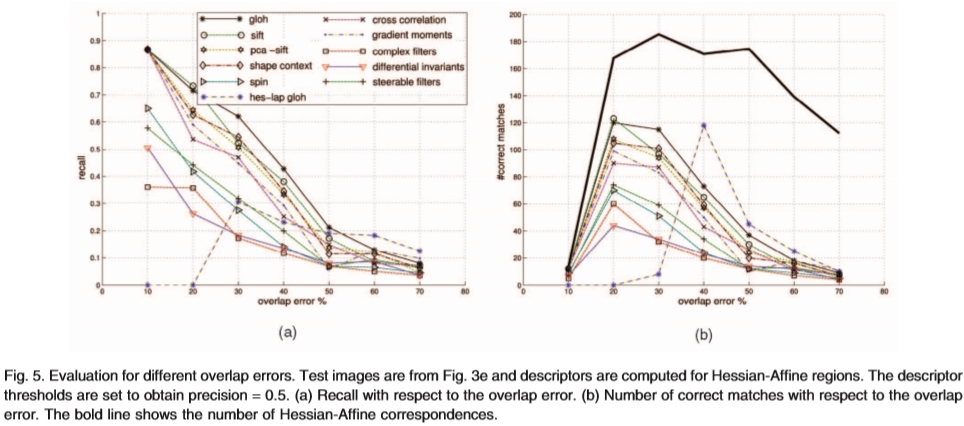
图5.不同重叠误差的评估。测试图像来自图3e，并且针对Hessian-Affine区域计算描述符。设置描述符阈值以获得精度= 0.5。 （a）回顾重叠错误。 （b）关于重叠误差的正确匹配数。粗线表示Hessian-Affine对应的数量

4.1.2区域重叠
在本节中，我们将研究重叠误差对描述符性能的影响。图5a显示了关于重叠误差的召回。为了测量不同重叠误差的调用，我们修复每个描述符的距离阈值，使得精度为0.5。图5b示出了针对0.5的误报率和针对不同重叠误差获得的正确匹配的数量。
对于一系列重叠误差计算正确匹配的数量以及对应的数量，即，对于大于10％且小于20％的重叠误差计算20％的分数。正如预期的那样，召回率随着重叠误差的增加而减小（参见图5a）。排名与之前的结果相似。我们可以观察到，互相关的回忆比其他高维描述符下降得更快，这表明该描述符对区域检测器精度的鲁棒性较低。我们还展示了GLOH与尺度不变的Hessian-Laplace探测器（hes-lap gloh）相结合的召回。由于没有相应的区域存在这种小错误，因此召回为零，重叠误差为20％。召回率在重叠率为30％时增加到0.3，对于较大的误差，召回量逐渐减少。 heslap gloh的召回略高于其他因为大的重叠误差主要是由圆形区域​​的尺寸差异引起的，不像仿射区域，其中误差也来自显着影响描述符的仿射变形。

图5b显示了不同重叠错误的正确匹配的实际数量。该图还反映了探测器的准确性。粗线表示用Hessian-Affine提取的相应区域的数量。几个相应的区域的误差低于10％，但其中近90％与基于SIFT的描述符，PCA-SIFT，矩和互相关正确匹配（参见图5a）。大多数相应的区域位于10％和60％的重叠误差范围内，而大多数正确的匹配位于10％到40％的范围内。在以下实验中，对应的数量在0％和50％重叠误差之间计算。我们允许50％的误差，因为如果它们以相同的结构为中心，那么具有这种重叠误差的区域可以匹配，这与被移位且仅部分重叠的区域不同。如果检测到的区域的数量高，则两个区域的意外重叠的概率也很高，尽管它们可以以不同的图像结构为中心。大范围的允许重叠误差导致大量的对应，这也解释了低召回率。

4.1.3维度
基于导数的描述符和复数滤波器可以按任意顺序计算。图6a显示了直到三阶和四阶计算的可控滤波器的结果，直到二阶和三阶的微分不变量，以及直到二阶和六阶的复数滤波器。这导致微分不变量的5,9维; 9,14可转向过滤器的尺寸;复杂滤波器的9,15维。我们使用了图3e中的测试图像，并为HessianAffine区域计算了描述符。注意，图6中的垂直轴是缩放的。计算到三级和四级之间的可操纵滤波器之间的差异很小但很明显。这表明三阶和四阶导数仍然是独特的。我们可以观察到不同阶数的微分不变量和复数滤波器的类似行为。计算到三阶的可操纵滤波器比根据相同顺序计算的差分不变量执行得更好。获得旋转不变性所必需的导数的乘法增加了不稳定性。

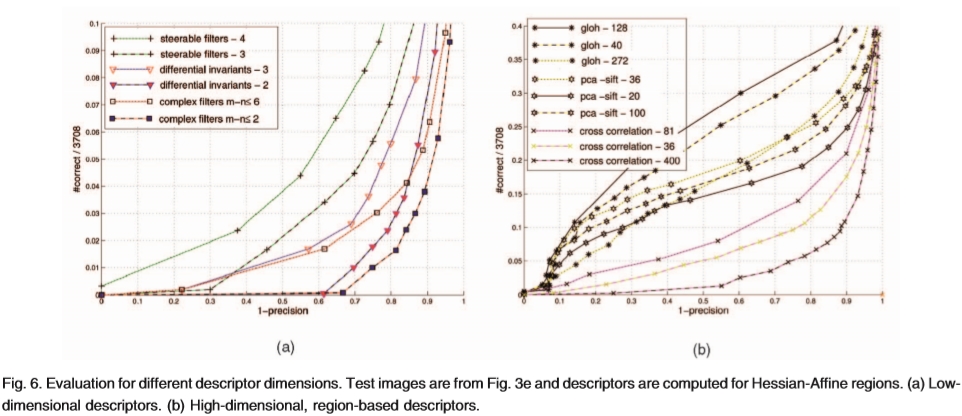
图6.不同描述符维度的评估。测试图像来自图3e，并且针对Hessian-Affine区域计算描述符。 （a）低维描述符。 （b）基于区域的高维描述符。

图6b显示了高维，基于区域的描述符（GLOH，PCA-SIFT和互相关）的结果。对17个位置区和16个方向计算GLOH描述符，并使用128个最大的特征向量（gloh-128）。如果仅使用40个特征向量（gloh-40），性能稍低，而对于所有272个维度（gloh-272）则低得多。对于PCA-SIFT和互相关，观察到类似的行为。评估36,81和400维度的互相关，即6 6,9 9和20 20个样本，结果最适合81维（9 9）。图6b显示该实验中的最佳维数为GLOH为128，PCASIFT为36，互相关为81。在下文中，我们使用在这里给出最佳结果的维数。

 表1描述符的独特性

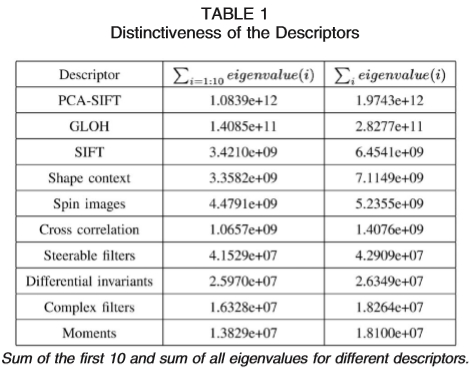
不同描述符的前10个和所有特征值之和的总和。

表1显示了前10个特征值的总和以及描述符的所有特征值的总和。这些特征值来自描述符的PCA，它们的方差归一化。表1中给出的数字对应于不同描述符捕获的方差量，因此对应于它们的独特性。 PCA-SIFT具有最大的总和，其次是GLOH，SIFT和其他描述符。时刻的价值最小。这反映了描述符的判别力，但稳健性同样重要。因此，描述符的排名在其他实验中可以是不同的。

 

4.1.4区域和场景类型
在本节中，我们评估不同仿射区域检测器和不同场景类型的描述符性能。图图7a和7b示出了具有Hessian-Affine和Harris-Affine区域的结构化场景的结果。图7c和7d分别用于Hessian-Affine和Harris-Affine地区的纹理场景。
对于纹理化场景（图7c和7d）的回忆比对结构化场景（图7a和7b）更好。对于结构化场景，检测到的区域的数量明显更大，其包含许多角落状结构。这导致区域之间的意外重叠，因此，存在大量的对应关系。这也意味着结构化场景的正确匹配的实际数量更大。纹理场景包含类似的图案，然而，这些区域捕获足够独特的信号变化。基于SIFT的描述符和其他描述符的性能差异在纹理场景上更大，这表明需要大的判别力来匹配它们。请注意，GLOH描述符在结构化场景上表现最佳，SIFT获得纹理图像的最佳结果。
针对Harris-Affine区域计算的描述符（参见图7d）给出比Hessian-Affine区域计算的稍差的结果（参见图7c）。对于结构化和纹理化场景都观察到这种情况。对于Harris和Hessian为基础的区域，尺度选择和仿射适应的方法是相同的。但是，如3.1节所述，基于拉普拉斯算子的比例选择与Hessian检测器相结合可以得到更准确的结果。

注意，在尺度不变区域上计算的GLOH描述符比许多其他描述符表现更差（参见图7a和7b中的hes-lap gloh和har-lap gloh），因为这些区域因此描述符只是尺度而不是仿射不变量。
4.2规模变化

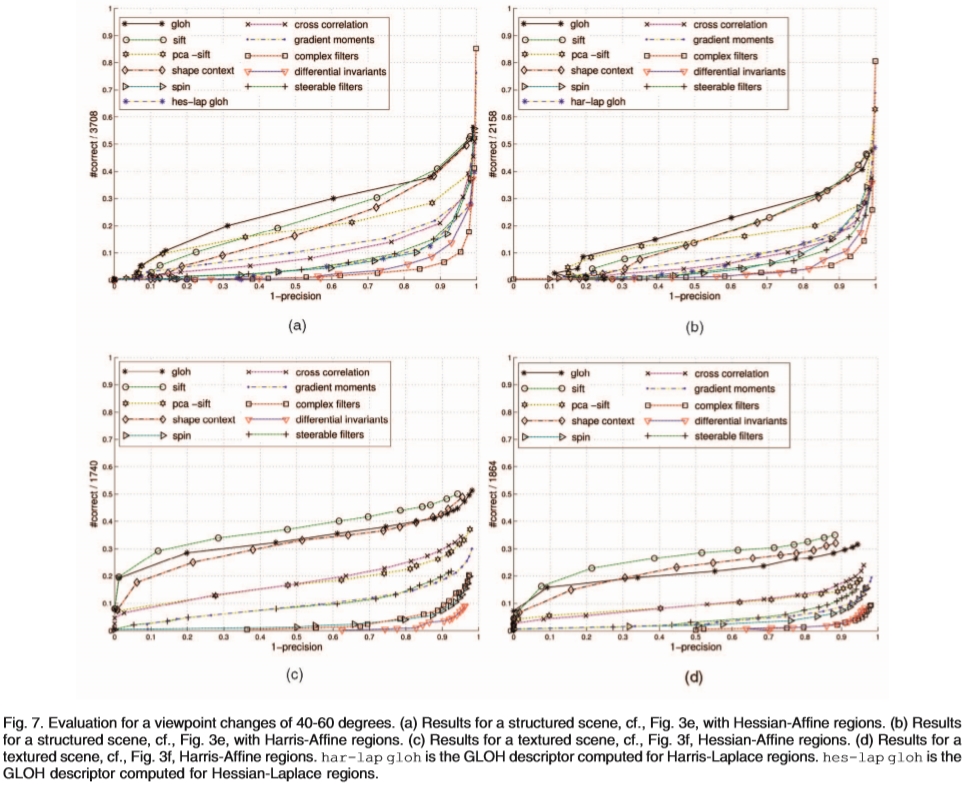
图7.评估40-60度的视点变化。 （a）结构化场景的结果，参见图3e，其中包含Hessian-Affine区域。 （b）结构化场景的结果，参见图3e，其中包含Harris-Affine地区。 （c）纹理场景的结果，参见图3f，Hessian-Affine区域。 （d）纹理场景的结果，参见图3f，Harris-Affine区域。 har-lap gloh是为Harris-Laplace区域计算的GLOH描述符。 hes-lap gloh是为Hessian-Laplace区域计算的GLOH描述符。
在本节中，我们将评估组合图像旋转和比例变化的描述符。比例变化位于2-2.5范围内，图像旋转范围为30度至45度。图8a示出了在纹理化场景（参见图3d）上在结构化场景（参见图3c）和图8c上检测到的Hessian-Laplace区域计算的描述符的性能。 Harris-Laplace区域用于图1和2中。 8b和8d。我们可以观察到GLOH在Hessian-Laplace区域上给出了最好的结果。在Harris-Laplace的情况下，如果1精度大于0.1，则SIFT和形状上下文获得更好的结果。其他描述符的排名是相似的。

我们可以观察到所有描述符的性能优于视点变化的情况。由于估计参数较少，因此区域更准确。与视点变化的情况一样，纹理图像的结果更好。然而，Hessian-Laplace的相应区域的数量是结构化场景上的Harris-Laplace的10倍，而纹理的场景上的相应区域的数量是Harris-Laplace的10倍。
在Harris-Affine（har-aff gloh）和HessianAffine（hes-aff gloh）检测到的仿射不变区域上计算的GLOH描述符获得的分数略低于在尺度不变区域上计算的基于SIFT的描述符，但它们的性能优于所有其他描述符。对于结构化和纹理化场景都观察到这种情况。这表明，如果与适当的描述符组合，也可以在存在比例变化的情况下使用仿射不变检测器。
4.3图像旋转
为了评估图像旋转的性能，我们使用旋转角度在30到45度范围内的图像。这代表了最困难的情况。在图9a中，我们比较了在结构化场景上检测到的标准Harris点的计算描述符（参见图3a）。所有曲线在相似的召回值下是水平的，即，所有描述符具有相似的性能。请注意，瞬间获得此场景类型的低分。应用的转换（旋转）不会影响描述符。召回低于1，因为许多通信是偶然建立的。哈里斯探测器发现许多点彼此接近，并且由于该区域的大尺寸（41个像素），许多支撑区域意外地重叠。

 

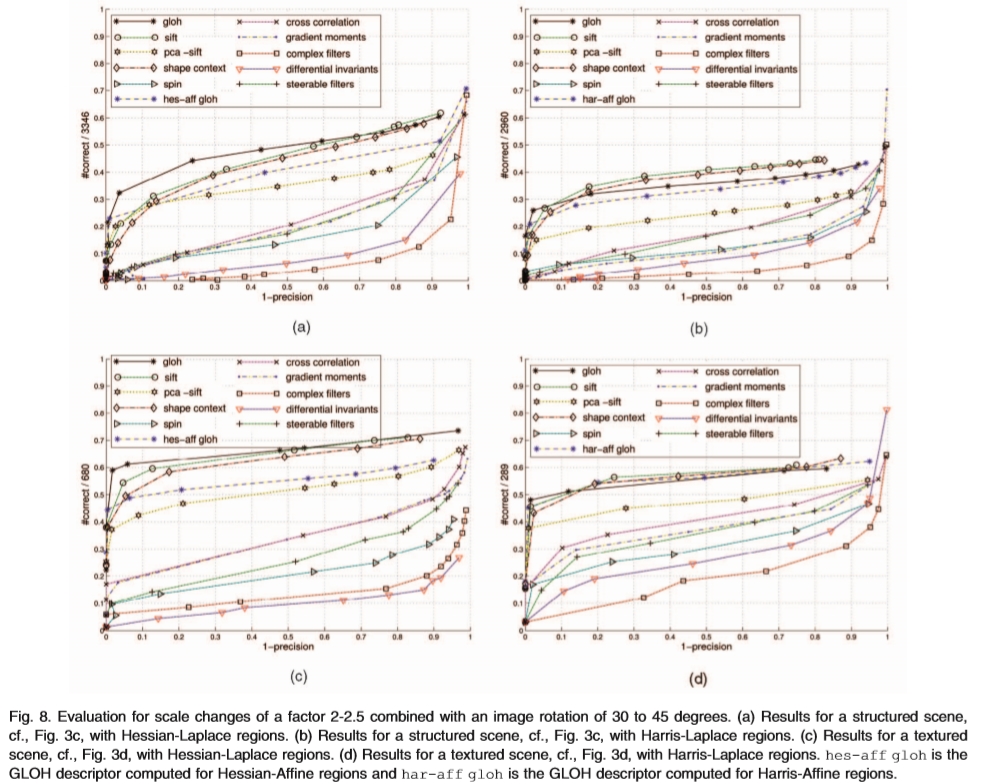
 图8.对因子2-2.5的比例变化的评估以及30至45度的图像旋转。 （a）结构化场景的结果，参见图3c，具有Hessian-Laplace区域。 （b）具有Harris-Laplace区域的结构化场景的结果，参见图3c。 （c）纹理场景的结果，参见图3d，具有Hessian-Laplace区域。 （d）纹理场景的结果，参见图3d，具有Harris-Laplace区域。 hes-aff gloh是为Hessian-Affine区域计算的GLOH描述符，har-aff gloh是为Harris-Affine区域计算的GLOH描述符。

 

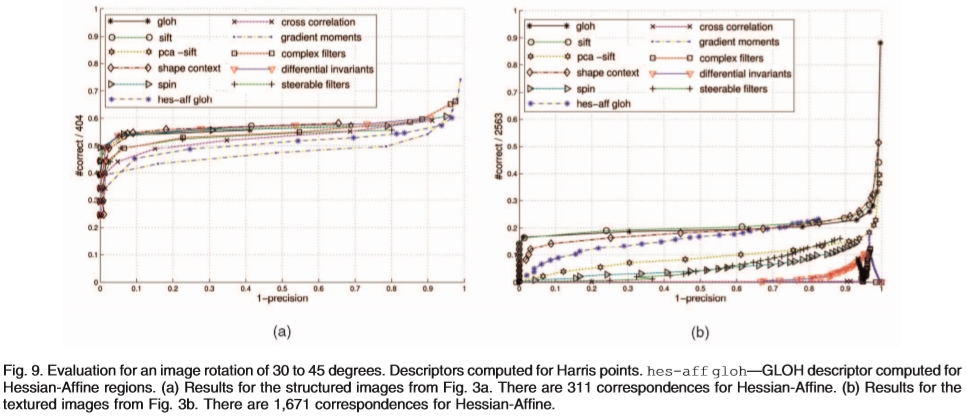
 图9.评估30至45度的图像旋转。哈里斯点的描述符计算。为Hessian-Affine区域计算的hes-aff gloh-GLOH描述符。 （a）来自图3a的结构化图像的结果。 Hessian-Affine有311对应的信件。 （b）来自图3b的纹理图像的结果。 Hessian-Affine有1,671个通讯符。

为了评估探测器误差的影响，我们显示了在Hessian-Affine区域上计算的GLOH描述符的结果（hes-aff gloh）。性能明显低于以Harris点为中心的固定大小补丁计算的描述符。定位的数量和角度估计。我们在图9a中注意到，这些误差对描述符性能的影响小于在Hessian-Affine情况下出现的区域误差。由于方向估计引起的误差很小，因为旋转不变描述符的表现不如非不变的描述符。

 

图9b显示了图3b中显示的扫描文本的结果。描述符的等级发生变化。 GLOH，SIFT和形状上下文获得最佳结果。在此示例中，时刻，微分不变量，互相关和复数滤波器失败。所有描述符的精度都很低。描述符不捕获纹理中的小变化，这导致许多错误匹配。在仿射不变区域（hes-aff gloh）上计算的GLOH描述符表现良好，即低于哈里斯点，但优于大多数其他描述符。

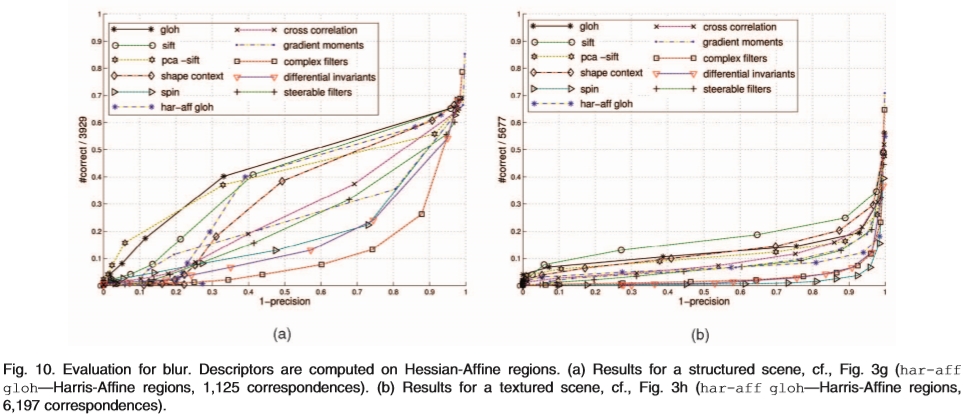
图10.模糊评估。描述符是在Hessian-Affine区域上计算的。 （a）结构化场景的结果，参见图3g（har-aff gloh-Harris-Affine地区，1,125份通信）。 （b）纹理场景的结果，参见图3h（har-aff gloh-Harris-Affine地区，6,197对应）。
4.4图像模糊
在本节中，将测量具有大量模糊的图像的性能。通过改变相机焦点介绍模糊。图10a示出了结构化场景的结果，图10b示出了纹理场景的结果。图像显示在图4和5中。分别为3g和3h。显示用HessianAffine检测的区域的结果。我们还显示了在Harris-Affine区域（har-aff gloh）上计算的GLOH的结果。
结果表明，尽管在这些图像中没有几何变换，但所有描述符都受到这种类型的图像劣化的影响。像素强度和局部结构的形状以不可预测的方式改变，并且描述符对这种变形不稳健。很难对这些变形进行建模，因此，人工生成数据的比较往往过于乐观。

GLOH和PCA-SIFT得分最高。与几何变化相比，基于边缘的形状上下文的性能显着降低（第4.1和4.2节）。在强烈模糊的情况下，边缘消失。在Harris-Affine地区计算的GLOH得分显着低于Hessian-Affine地区。模糊对Harris-Affine探测器的性能影响大于对Hessian-Affine探测器的性能影响。在[33]中也进行了类似的观察。
纹理场景的结果（参见图10b）更受模糊的影响。描述符不能区分检测到的区域，因为模糊使它们几乎相同。 SIFT在此场景中提供最大数量的匹配。互相关在高维描述符中获得最低分，但高于低维描述符。
4.5 JPEG压缩

在图11中，我们评估JPEG压缩对结构化场景的影响（参见图3i）。转换图像的质量是参考图像的5％。显示用Hessian-Affine检测的区域的结果。描述符的性能优于模糊（参见4.4节），但比结构化场景的旋转和比例变化更糟（参见4.3节和4.2节）。随着所有描述符的精度降低，性能逐渐增加，即，所有描述符都受到JPEG伪像的影响。 PCA-SIFT获得低假阳性率的最佳分数，SIFT获得高于0.2的假阳性率。 GLOH的结果位于这两个描述符之间。

 

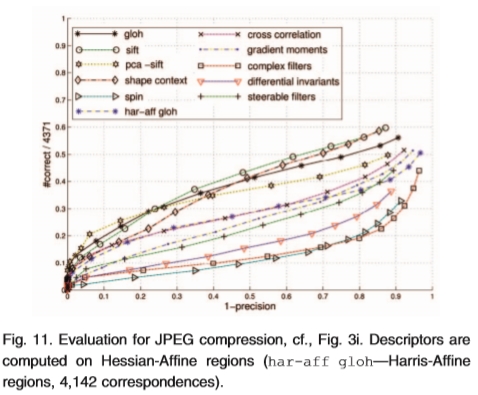
图11. JPEG压缩的评估，参见图3i。在Hessian-Affine区域上计算描述符（har-aff gloh-Harris-Affine region，4,142对应）。

图12.对照明变化的评估，参见图3j。描述了Hessian-Affine区域的描述符（har-aff gloh-Harris-Affine区域，1,120个对应关系）。 （a）差分描述符的照明不变性。可控滤波器和微分不变量是在强度归一化区域上计算的标准描述符。不变的可控滤波器和不变的微分不变量是光照不变量而不是不变的可控滤波器，而不是不变的微分不变量不是强度归一化的。 （b）在照明归一化区域上计算的描述符。

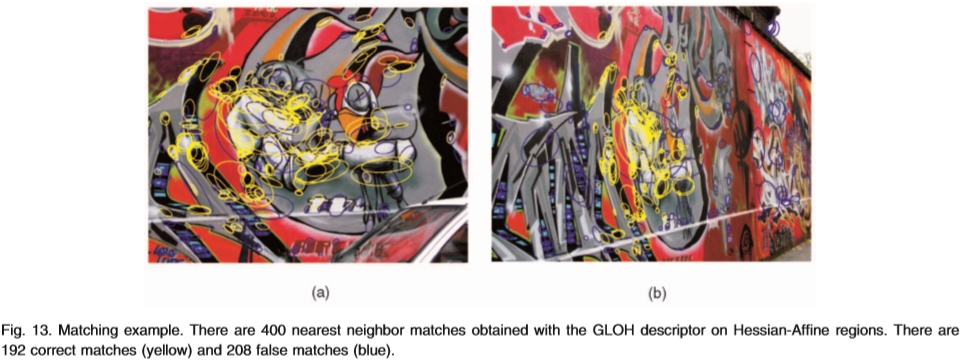
图13.匹配示例。在Hessian-Affine区域上使用GLOH描述符获得了400个最近邻居匹配。有192个正确匹配（黄色）和208个错误匹配（蓝色）。

4.6照明变化
图12示出了通过改变相机设置获得的照明变化的结果。图像对显示在图3j中。为Hessian-Affine区域计算描述符。图12a比较了两种获得差分描述符仿射光照不变性的方法：1）基于区域归一化（可操纵滤波器和我们所有比较中使用的差分不变量）和2）基于描述符的不变性（不变可控滤波器和不变量）微分不变量），详见3.1节。我们观察到在归一化区域上计算的描述符明显更好。从理论上讲，这两种方法是等价的。然而，由于区域和位置误差以及非仿射照明变化，导数的比率放大了噪声。通过与不是强度归一化的描述符（不是不变的可操纵滤波器，而不是不变的微分不变量）的比较来显示仿射光照不变性的重要性。这些描述符获得了更糟的结果。得分不为零，因为这些描述符基于从强度中消除常数因子的导数。
在图12b中，在存在照明变化的情况下比较标准描述符。所有描述符都是在标准化图像块上计算的。 GLOH获得最佳匹配分数。在Harris-Affine区域上计算的相同描述符获得等效分数。
4.7匹配示例

该部分示出了视点变化大于50度的图像的匹配示例，参见图13.Hessian-Affine分别在左图像和右图像中检测2,511和2,337个区域。根据第3.3节中定义的重叠标准确定了747个对应关系。对于用GLOH描述符获得的400个最近邻居匹配，192是正确的（在图13中以黄色显示）并且208是假的（以蓝色显示）。
表2显示了回忆，误报率和使用不同描述符获得的正确匹配的数量。这些结果都基于固定数量的400个最近邻居匹配。 GLOH获得0.25的最高召回率，通过SIFT和形状背景获得略低的分数。复杂过滤器的得分最低为0.06。正确匹配的数量从192到44不等。复杂滤波器的正确匹配数比GLOH少约4.4倍。这清楚地显示了基于SIFT的描述符的优势。

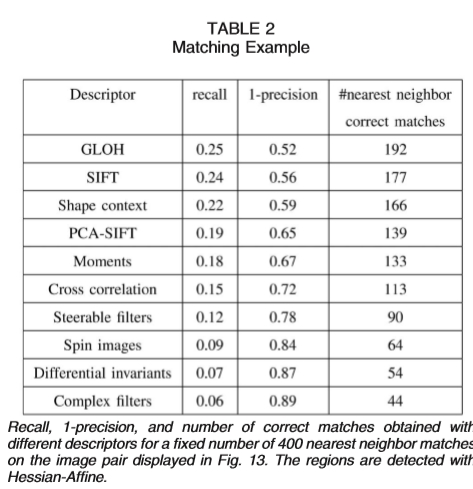
回想一下，对于图13中所示的图像对上的固定数量的400个最近邻匹配，使用不同描述符获得的1精度和正确匹配的数量。用Hessian-Affine检测区域。

5讨论和结论
在本文中，我们提出了在存在真实几何和光度变换的情况下对感兴趣区域描述符的实验评估。目标是比较用最近提出的尺度和仿射不变检测技术提取的区域计算的描述符。请注意，评估是为匹配和识别同一对象或场景而设计的。
在大多数测试中，GLOH获得最佳结果，紧随其后的是SIFT。这显示了基于区域的SIFT描述符的鲁棒性和独特性。形状上下文也显示出高性能。但是，对于纹理场景或边缘不可靠时，其得分较低。
最好的低维描述符是梯度矩和可控滤波器。当基于直方图的描述符的高维度成为问题时，可以将它们视为替代方案。微分不变量给出的结果明显比可操纵滤波器差，这是令人惊讶的，因为它们基于相同的基本分量（高斯导数）。获得旋转不变性所必需的导数的乘法增加了不稳定性。
互相关会产生不稳定的结果性能取决于感兴趣点和区域检测的准确性，其对于显着的几何变换而言降低。与其他高维描述符相比，互相关对这些错误更敏感。

由Hessian-Laplace和Hessian-Affine检测到的区域主要是斑点状结构。斑点中心没有明显的信号变化，因此描述符在较大的邻域上表现更好。由于其较高的准确性，Hessian区域的结果略微但系统性地好于Harris区域。
对于不同的匹配策略，描述符的排名是相似的。我们可以观察到，如果最近邻距离比用于阈值处理，则SIFT给出相对更好的结果。注意，基于最近邻居的匹配的精度高于基于阈值的匹配。

显然，这里给出的比较并不详尽，包含更多场景类别会很有趣。然而，该比较似乎表明基于区域的稳健描述符比逐点描述符表现更好。相关性是最简单的基于区域的描述符。但是，我们的比较表明它对区域错误很敏感。包括与贴片对齐的相关性将是有趣的，其校正这些误差并测量通过这种对准获得的增益。当然这非常耗时，只能用于验证。
应该对物体和场景类别的识别和分类进行类似的实验。在纹理分类和类似局部结构分类的背景下对描述符的评估将是对我们的工作有用且有价值的补充。这可能意味着基于描述符和对这些聚类的评估来聚类局部结构。在[21]，[44]中提出的评估框架中比较基于SIFT的描述符也是有趣的。

致谢
该研究得到了欧洲FETopen项目VIBES和欧洲项目LAVA（IST-2001-34405）的支持。

 

有关此计算主题或任何其他计算主题的更多信息，请访问我们的数字图书馆，网址为：www.computer.org/publications/dlib。