Image Processing and Analysis_8_Edge Detection：Local Scale Control for Edge Detection and Blur Estimation——1998

此主要讨论图像处理与分析。虽然计算机视觉部分的有些内容比如特 征提取等也可以归结到图像分析中来，但鉴于它们与计算机视觉的紧密联系，以 及它们的出处，没有把它们纳入到图像处理与分析中来。同样，这里面也有一些 也可以划归到计算机视觉中去。这都不重要，只要知道有这么个方法，能为自己 所用，或者从中得到灵感，这就够了。

8. Edge Detection
边缘检测也是图像处理中的一个基本任务。传统的边缘检测方法有基于梯度 算子，尤其是 Sobel 算子，以及经典的 Canny 边缘检测。到现在，Canny 边缘检 测及其思想仍在广泛使用。关于 Canny 算法的具体细节可以在 Sonka 的书以及 canny 自己的论文中找到，网上也可以搜到。最快最直接的方法就是看 OpenCV 的源代码，非常好懂。在边缘检测方面，Berkeley 的大牛 J Malik 和他的学生 在 2004 年的 PAMI 提出的方法效果非常好，当然也比较复杂。在复杂度要求不高 的情况下，还是值得一试的。MIT的Bill Freeman早期的代表作Steerable Filter 在边缘检测方面效果也非常好，并且便于实现。这里给出了几篇比较好的文献， 包括一篇最新的综述。边缘检测是图像处理和计算机视觉中任何方向都无法逃避 的一个问题，这方面研究多深都不为过。
[1980] theory of edge detection
[1983 Canny Thesis] find edge
[1986 PAMI] A Computational Approach to Edge Detection
[1990 PAMI] Scale-space and edge detection using anisotropic diffusion
[1991 PAMI] The design and use of steerable filters
[1995 PR] Multiresolution edge detection techniques
[1996 TIP] Optimal edge detection in two-dimensional images
[1998 PAMI] Local Scale Control for Edge Detection and Blur Estimation
[2003 PAMI] Statistical edge detection_ learning and evaluating edge cues
[2004 IEEE] Edge Detection Revisited
[2004 PAMI] Design of steerable filters for feature detection using canny-like criteria
[2004 PAMI] Learning to Detect Natural Image Boundaries Using Local Brightness, Color, and Texture Cues
[2011 IVC] Edge and line oriented contour detection State of the art

 

翻译

用于边缘检测和模糊估计的局部比例控制

作者：IEEE成员James H. Elder和IEEE研究员Steven W. Zucker

 

摘要 -边缘检测的标准方法基于强度变化较大的边缘模型。这种方法无法可靠地检测和定位自然图像中的边缘，其中模糊比例和对比度可能会在很大范围内变化。主要问题在于，用于局部估计的合适空间比例取决于边缘的局部结构，因此在图像上发生不可预测的变化。在这里，我们表明，可以利用传感器属性和操作员规范的知识来定义唯一的，可本地计算的最小可靠标度，以便在图像中的每个点进行局部估计。这种用于局部比例控制的方法被应用于检测和定位具有浅景深和阴影的图像中的边缘的问题。我们显示，可以通过单个系统准确地恢复跨越较大范围的模糊比例和对比度的边缘，该系统无需输入参数即可获得第二个传感器噪声。这种方法的自然好处是可以测量轮廓的厚度，该轮廓可以用于估计焦点和半影模糊。局部比例控制对于估计复杂图像中的模糊非常重要，因为潜在的非常不同的模糊比例之间的相邻边缘之间发生干扰的可能性要求以最小的可靠比例进行估算。

索引词-边缘检测，定位，缩放空间，模糊估计，散焦，阴影。

 

1 引言
边缘检测器通常设计为恢复图像中的台阶不连续性（例如[1]，[2]，[3]，[4]），但是，世界上物理结构的边界通常不会像台阶一样投射到图像上不连续性。图1的左侧描绘了笔直的，锋利的反射边缘，该边缘略微偏离所示透镜系统的物平面，因此物理边缘作为模糊的亮度过渡投影到图像上。在图1的中央，显示了由球形光源投射到平坦地面上的直边物体的阴影。由于光源不是点光源，因此阴影具有半影，从而使阴影边缘显得模糊。右侧显示了一个略为圆形的对象边缘，当从上方进行照明和观察时，该边缘还会在图像中产生模糊的边缘。

图1：世界上的边缘通常会在空间上模糊地投射到图像上。 从左到右：由于景深有限而造成的焦点模糊； 阴影边缘的半影模糊； 阴影在平滑的对象边缘处模糊。

由于相机和眼睛的景深有限，因此光源很少是点光源，并且物体通常很光滑，随着模糊的亮度过渡，世界上的边缘通常会投射到图像上。本文概括了台阶间断的检测，以涵盖这种更广泛，更实际的边缘类别。

 首先，重要的是要区分在边缘可以局部计算和不能局部计算的内容。我们已经证明[5]，实际上在图1所示的焦点模糊和投射阴影场景之间存在二重性。在这种二重性下，可以将构成投射阴影模型的光源，遮挡物和地平面分量交换为孔径，反射率边缘和传感器平面组成了焦点模糊的几何光学模型。具体来说，两种情况都可以预测出完全相同形式的S型亮度过渡：

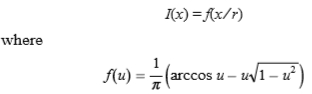
也可以显示阴影对象边缘来模仿此强度模式[5]。

该方程式中的参数r 确定边缘的模糊程度。对于焦点模糊的情况，r 由光圈的大小以及镜头，像平面和传感器平面之间的相对距离确定。对于投射阴影，相关的变量是光源的视角以及遮光器和地面之间的距离。对于阴影边缘，r由曲面的曲率确定。在自然场景中，这些变量可能采用宽范围的值，从而在宽范围的模糊比例上产生边缘。

我们的结论是双重的。首先，随着S形亮度在很宽的模糊范围内过渡，世界上的边缘通常会投射到图像上。其次，我们不能将局部计算的目标局限于检测特定类型的边缘（例如，遮挡边缘），因为我们期望不同类型的边缘在本地是无法区分的。因此，局部计算的目标必须是在这种宽泛的条件范围内检测，定位和表征所有边缘，而不管它们从中投影的物理结构如何。

为了说明实现此目标所面临的挑战，请考虑图2所示的场景。由于光源不是点光源，因此投射阴影的轮廓并不是均匀锐利的。明显的模糊当然是阴影的半影：阴影表面的区域，其中光源仅部分被遮盖。

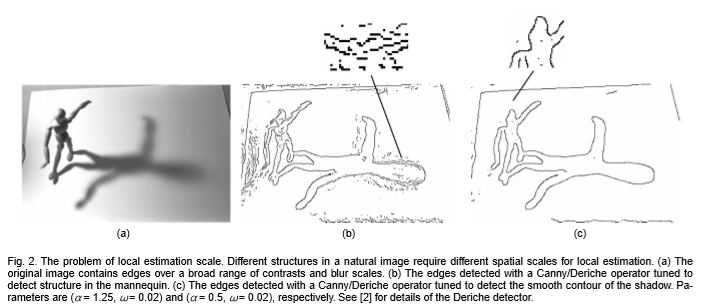
图2：局部估计规模问题。 自然图像中的不同结构需要不同的空间比例来进行局部估计。 （a）原始图像的对比度和模糊度范围很大。 （b）使用Canny / Deriche算子对边缘进行检测，并对其进行调整以检测人体模型中的结构。 （c）使用Canny / Deriche运算符检测到的边缘经过调整以检测阴影的平滑轮廓。 参数分别为（α= 1.25，ω= 0.02）和（α= 0.5，ω= 0.02）。 有关Deriche检测器的详细信息，请参见[2]。

图2b显示了Canny / Deriche边缘检测器[1]，[2]生成的边缘图，已对其进行调整以检测人体模型的细节（通过反复试验调整比例参数和阈值以提供最佳结果） 。在相对较小的比例下，阴影的轮廓无法可靠地解析，并且在人体模型后面以及前景和背景中的平滑强度梯度被检测为许多短而不相交的曲线。图2c显示了Canny / Deriche边缘检测器生成的边缘图，该边缘图经过调整以检测阴影的轮廓。在这种较大的比例下，人体模型的细节无法恢复，并且阴影的轮廓在一只手臂下方的高曲率部分处破碎了。

此示例表明，要处理自然图像，必须使用多个比例的运算符。这一发现进一步得到了以下发现的支持：猫[6]和灵长类动物[7]的早期视觉皮层中神经元的感受野散布在几个八度的大小上。尽管许多计算机视觉研究人员已经得出了这一结论（例如[8]，[1]，[9]，[10]，[11]，[12]），但问题一直存在，并且仍然是：比例空间已计算出来，如何使用？是否有原则上的方法可以按比例组合信息或在此比例空间内进行推理，以生成有关图像的可用断言？

在本文中，我们基于两个目标开发了一种新的局部尺度适应方法：
1）显式测试局部推断的统计可靠性。

2）最小化由于邻近图像结构引起的局部估计中的失真。

这种可靠的估计方法构成了将边缘检测推广到在广泛的模糊比例和对比度范围内检测自然图像边缘的基础。我们的最终目标是检测自然图像中的所有强度边缘，而不考虑其物理原因（例如，遮挡，阴影，纹理）。

 

2 边缘检测中的尺度空间方法

规模问题在几种最著名的边缘检测理论中扮演着重要角色。 Marr和Hildreth [8]使用高斯算子的拉普拉斯算子来构造多个尺度的零交叉线段，并提出，如果线段存在于连续尺度范围内的特定位置和方向，则断言物理边缘的存在。 Canny [1]在亮度函数的一阶导数的方向最大值处定义了边缘，并提出了一个复杂的规则系统来组合在多个尺度上检测到的边缘。这些方法的主要问题是难以区分不同比例的附近响应是对应于一条边还是多个边。

应用于边缘检测的连续尺度空间方法也趋于复杂[13]。在各向异性扩散网络[14]中，每个点的扩散速率由时空导系数决定，该系数是该点亮度函数估计梯度幅度的递减函数。因此，高梯度的点比低梯度的点平滑。虽然这显然是用于图像增强的强大框架，但我们的目标不是锐化边缘，而是在广泛的模糊和对比度下检测边缘。为此，各向异性扩散的最令人困扰的特性是它隐含地使用亮度梯度上的唯一阈值，低于该阈值则梯度会随时间减小（平滑），超过此阈值则会随时间增加（边缘增强）。不幸的是，由于重要的边缘会产生由对比度和模糊度决定的宽范围的梯度，因此即使对于单个图像，也没有原则上选择该阈值的方法。另一方面，传感器噪声会产生非常陡峭的梯度。

边缘聚焦方法[11]，[15]将为匹配问题而开发的从粗到精跟踪的概念应用于边缘检测问题。该方法是选择一些“真正重要的”事件（例如，零交叉）（即，大规模生存），然后在尺度减小时通过尺度空间跟踪这些事件，以将事件准确地定位在空间。

除了这种方法的计算复杂性外，将其应用于边缘检测还存在两个主要问题。首先，对于边缘而言，尺度与意义没有可靠的对应关系。通常，如果边缘具有高对比度，聚焦并孤立，它们将以更高的比例保留下来。但是，对比度不是很重要的指标，因为具有相似反射功能的对象在被遮挡时会产生非常低的对比度边缘。这是经常发生的部分原因是由于自我遮挡以及具有相似反射功能的对象经常在世界中分组在一起（例如，现在您面前的页面）。尽管可以说重要的对象应该成为焦点，但在实际情况下这通常是不可能的。最后，边缘的隔离也并不表示重要性：一个对象与另一个对象的接近通常不会降低任何一个对象的重要性。因此，使用比例尺空间的高端来选择边缘重要性是不合适的。

第二个问题在于以下假设：可以在最佳规模上获得最佳定位精度。的确，由于与邻近事件的相互作用，事件的轨迹在粗略尺度上倾向于在空间中徘徊，但精确度随尺度的精确变化在很大程度上取决于邻近事件相对于传感器噪声水平的分离[1]。 。如果事件间隔较大，则定位精度实际上会随比例增加。如果传感器噪声很高，则在较小的比例下定位精度可能会非常差。

 

Jeong和Kim [16]提出了一种自适应方法，用于估计图像中每个点的边缘检测的唯一比例。他们提出的问题是整个图像的功能最小化，并使用松弛方法来解决由此产生的非凸优化问题。作者报告说，他们的结果受到目标函数形状复杂以及所选标度对初始猜测的敏感性的影响。

最近，林德伯格提出了一种基于最大化边缘强度的启发式度量来选择用于边缘检测的局部尺度的方法[17]，[18]。这种方法的主要困难在于，如此选择的比例尺通常太小而无法提供边缘检测所基于的导数的可靠估计，从而导致包含许多人为边缘的密集边缘图。为了将真实边缘与伪像区分开，Lindeberg提出了一个更全局的检测后阶段，在该阶段中定义了沿边缘有效程度的度量，并沿连接的像素链进行积分。然后，只有高于（未指定）阈值的边缘链才被认为是重要的。相比之下，我们本文的目标是开发一种完全局部的比例尺选择方法，该方法不需要这种后处理试探法即可将真实边缘与伪像区分开。

因此，我们可以通过以下观察总结出我们在边缘检测中偏离尺度问题的标准方法：

1）不存在可以先验定义以区分边缘和非边缘的自然尺度或梯度阈值。

2）大范围的生存无法区分重要边缘和无关紧要边缘。

3）一般而言，本地化并不是最好的最佳规模。

4）为避免人为因素，选择的比例必须足够大以提供可靠的导数估计。

 

3 最低可靠度

从诸如图2的图像可靠地恢复结构的困难在于，用于估计的适当比例在图像上变化。但是，尽管图像结构的比例是随空间变化的，但用于从场景生成图像的系统是固定的。这是计算机视觉中的典型情况：一个人不知道“外面有什么”，但是一个人知道传感器的属性，因此可以预先计算传感器噪声的统计数据[19]。给定要检测的事件的特定模型（在这种情况下为亮度边缘），并为此目的使用了适当的运算符，则可以将模型的参数与事件可以在其上发生变化的唯一最小尺度相关联。被可靠地检测到。我们称此唯一标度为事件的最小可靠标度。

此处所说的可靠，是指在此范围内以及更大范围内，由于传感器噪声引起的错误可能性低于标准公差（例如，整个图像的误差为5％）。该定义不考虑由于图像附近场景事件的影响而导致错误声明的危险，在任何带宽受限的系统中，场景事件必定是比例的递增函数。尽管其他人已经尝试对这种现象进行显式建模[1]，但我们认为该问题不太可能接受这样的一般解决方案。例如，尽管一组图像可以产生边缘之间的预期间隔的估计，但是如果该集合的样本包含细灯芯绒图案，则该估计将没有什么用处。我们认为不应使用这种不确定的先验，而应使用提供可靠估计的最小尺度。通过在图像的每个点选择最小的可靠比例，我们可以防止传感器噪声引起的误差，同时将附近结构的干扰引起的误差降至最低。

通过确定用于局部估计的唯一尺度，我们避免了在多个尺度上组合响应[8]，[1]或通过尺度空间[11]，[15]跟踪边缘所需的复杂性和临时决策。由于计算完全是局部的，因此我们避免了Jeong和Kim [16]提出的全局计算的复杂性。通过遵循关于传感器噪声可靠性的严格标准，我们避免了使用复杂的后处理试探法来区分真实边缘和人为边缘的需求[18]。

4 建模边缘，模糊和感应

边缘被建模为未知振幅A 和基座偏移B 的阶跃函数 Au（x）+ B，出于讨论的目的，该边缘将与图像坐标系的y轴对齐。该边缘的焦点或半影模糊由高斯模糊核 ¹ 建模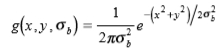

比例常数σ_b的未知数，以生成误差函数

传感器噪声 n（x，y）被建模为平稳的加法零均值白噪声过程；也就是说，图像中给定点处的噪声是具有标准偏差s_n 的正态分布随机变量，与信号和图像中其他点处的噪声无关。因此，完整的边缘模型为：

 

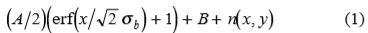
估计成像系统的传感器噪声统计数据相对简单。对于图2中使用的系统，首先选择平坦平面的散焦图像区域。然后使用单位功率内核双抽头滤波器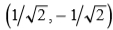对子图像进行高通滤波。该子图像上的阴影变化缓慢，散焦充当额外的低通滤波器，因此我们可以确信场景结构对滤波器输出的贡献可忽略不计。然后利用随机过程理论的以下基本结果：

提案1：线性变换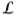的结果的标准偏差：ℜⁿ→ℜ应用于一组i.i.d.标准偏差的随机变量s_n是线性变换的L₂范数与随机变量的标准偏差的乘积：

证明很简单[23]。

因此，单位功率滤波器输出的统计信息提供了传感器噪声统计信息的估计值：图2所示的八位图像的噪声标准偏差约为1.6量化级别。

 

1.高斯模型与第1节中讨论的焦点和半影模糊的几何模型不同。有人认为，高斯模型可以更好地说明实际成像系统中的各种像差，并且已广泛用于从深度到深度的成像。 散焦工作[20]，[21]，[22]。
2.我们将高斯函数既用作传感器噪声概率分布的模型，又用作局部估计的平滑函数。 为了清楚起见，当符号s被用作噪声模型时，符号s用于高斯的标准偏差；当符号s被用作平滑滤波器时，符号σ用于高斯的比例。

5 可靠性标准
我们的边缘检测方法依赖于对图像中每个点上的强度函数的局部形状做出可靠的推断。可靠性是根据整个图像的总体显着性水平α_I 和逐点显着性水平α_p来定义的。我们将整个图像的整体图像显着性水平α_I 固定为整个图像的5％，即我们要求在所有图像点上犯下一个或多个I型（假阳性）错误的可能性小于5％。根据i.i.d.噪声，则图像中的像素数n决定了逐点显着性水平：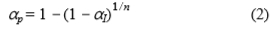

为简单起见，我们将α_p固定为由实验中使用的最大图像尺寸确定的恒定值：n = 512×512像素→α_p = 2.0×10^-7。这确保了本文使用的所有图像的总体显着性水平α_I 均小于5％。

6 局部规模控制和梯度检测

在图像中特定位置声明边缘的必要条件是亮度函数中的非零梯度。可以使用可控的高斯一阶导数基础滤波器[24]，[25]估算梯度：

其中σ₁表示一阶导数高斯估计量的标度。可以将一阶导数高斯滤波器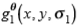在任意方向θ 上对图像I（x，y）的响应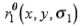精确地计算为基础的加权和过滤响应，以便

在亮度函数的非平稳点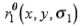，在θ上具有唯一的最大值，在梯度方向θ_M（x,y,σ₁）上获得的梯度大小 ：

为了确信在图像 I（x，y）的一个点（x，y）上存在一个非零梯度，我们必须考虑梯度算子的响应可能仅由于噪声引起的可能性。由于梯度算子是非线性的，因此计算变得复杂，因此其响应将不会呈正态分布。但是，可以通过利用概率论的第二个基本结果来确定其分布[26]：

命题2.令U为pdf p_U的随机变量，U∈A⊆ℜ。令V = f（U），其中f 在A 上是亚纯的。然后，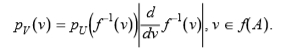

该命题可用于推导对噪声的梯度响应分布。我们让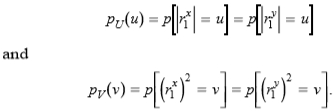

如果图像仅包含高斯i.i.d.标准差s_n的噪声，U将具有半高斯分布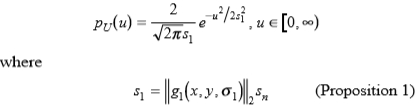

由于f（u）= u²在[0，∞）上是微晶的，因此命题2

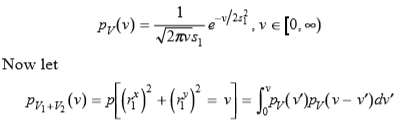
解决积分，我们得到

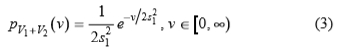
为了确保α_p 的点状显着性，我们需要一个临界值c₁，在该临界值以下，响应不被认为是可靠的，满足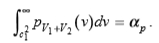


代入（3）并求解

替代α_p = 2.0×10⁻⁷（第5节），我们得到c₁ = 5.6s₁。一阶导数算子的L₂范数由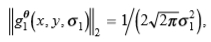

因此，我们有以下内容。

定义1.非线性高斯梯度算子的临界值函数c₁（σ₁）跟踪该算子的统计可靠性阈值（α= 0.05）作为尺度的函数，其公式如下：

对于给定的传感器噪声水平和操作人员规模，临界值函数指定了可以认为统计上可靠的最小响应值。为了使临界值函数与边缘检测相关，我们必须考虑梯度算子对边缘的响应。给定沿幅度A的y轴的阶跃边缘模糊和模糊参数σ_b，则梯度幅度由下式给出

在y轴上达到最大值：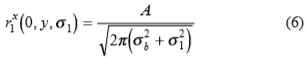

因此，虽然对模糊边缘的最大梯度响应（6）和临界值函数（4）都随估计规模的增加而减小，但临界值函数下降得更快，反映了较大定向算子的改进的信号检测性能。通过将（6）与（4）组合并求解σ₁，我们得出了命题3。

命题3.对于具有标准偏差为s_n的白色传感器噪声，幅度为A且模糊参数为σ_b的边缘的成像系统，存在最小可靠标度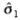，在该最小可靠标度下可以可靠地检测亮度梯度：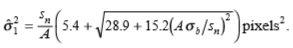

示例边缘的这种情况在图3a中示出。估计边缘梯度的最小可靠标度由标度确定，在该标度下，边缘响应刚好超过显着性阈值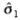： =2.1像素， 在这种情况下。

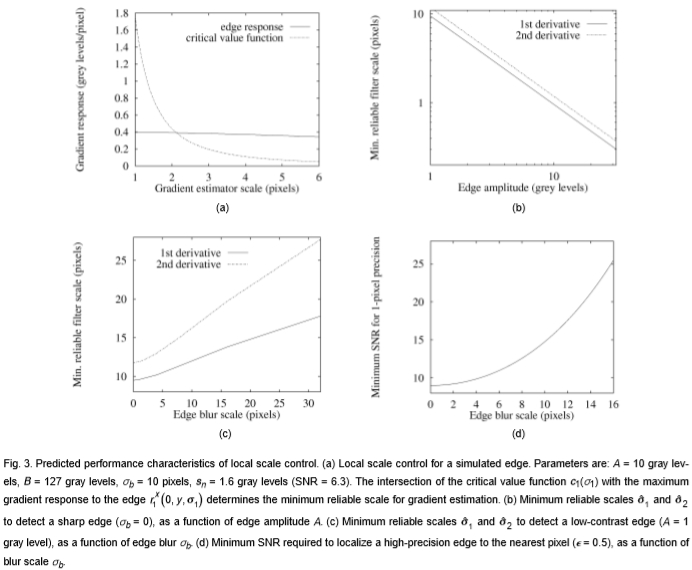
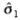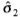图3：局部比例控制的预测性能特征 （a）用于模拟边缘的局部比例控制。 参数为：A = 10个灰度级，B = 127个灰度级，σ_b = 10个像素，s _n = 1.6灰度级（SNR = 6.3）。 临界值函数c₁（σ₁）与对边缘r₁^x（0,y,σ₁），s_n= 1.6的最大梯度响应的交点确定了用于梯度估计的最小可靠标度。 （b）最小可靠标度和作为边缘振幅A的函数，用于检测锐边（σ_b = 0）。 （c）作为边缘模糊σ_b的函数的最小可靠标度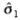和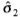以检测低对比度边缘（A = 1灰度级）。 （d）作为模糊比例σ_b的函数，将高精度边缘定位到最近像素所需的最小SNR（ = 0.5）。

注意，由于边缘的幅度A也是未知的，因此准确地估计最小可靠标度不允许人们估计边缘σ_b的模糊。因此，在我们的实验中，我们仅尝试通过在刻度的倍频程间隔计算梯度估计来保持接近最小可靠比例，在每个点上使用梯度估计超过临界值函数的最小尺度，即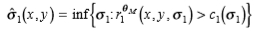

图4：带阴影的人体模型图像的局部比例控制结果。 对于比例尺地图，较大的比例尺以浅灰色呈现，白色表示无法进行可靠的估计。 （a）用于梯度估计的最小可靠尺度图。 （b）二阶导数估计的最小可靠规模图。 （c）检测到的边缘。 请注意，人体模型的精细细节和模糊的低对比度阴影都可以可靠地恢复。

使用局部比例控制对人体模型和阴影图像进行梯度计算的结果如图4a所示。使用了六个标度：σ₁∈{0.5，1，2，4，4，8，16}像素。此处的灰色阴影表示梯度估计可靠的最小比例，黑色表示σ₁ = 0.5像素，较浅的阴影表示较高的比例，而白色表示无法进行可靠的估计。尽管最小的比例尺对于人体模型的轮廓是可靠的，但需要更高的比例尺才能完全恢复阴影。

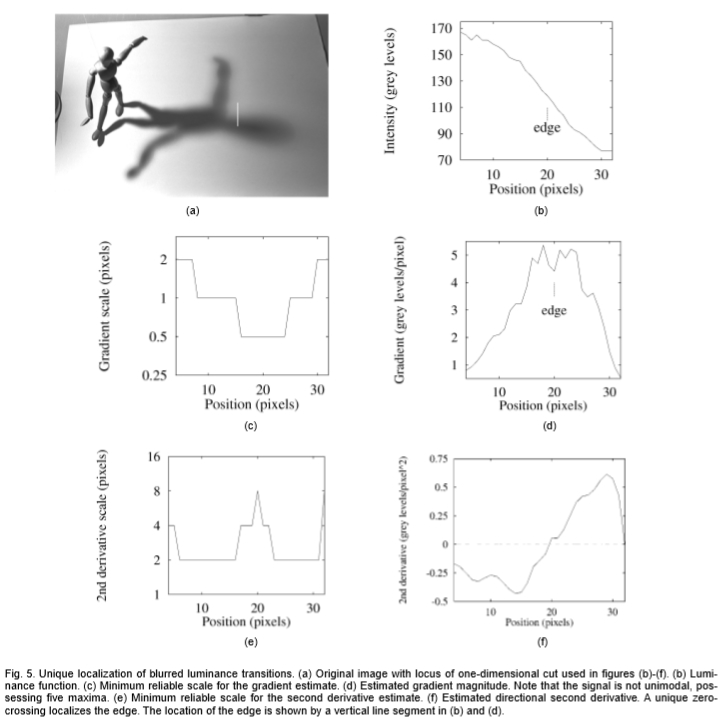
图5：模糊过渡的唯一定位。 （a）图（b）-（f）中使用的具有一维切割轨迹的原始图像。 （b）亮度功能。 （c）梯度估计的最小可靠标度。 （d）估计的梯度幅度。 请注意，信号不是单峰的，具有五个最大值。 （e）二阶导数估计的最小可靠标度。 （f）估计方向二阶导数。 独特的过零会定位边缘。 边缘的位置由（b）和（d）中的垂直线段显示。

许多边缘检测器（例如[1]）将边缘定义为梯度图中的局部最大值。图5显示了这种方法为什么行不通的原因。已选择阴影半影的一维横截面，以检查微分响应的行为和用于局部估计的最小可靠标度。图5b示出了横截面的亮度分布，图5d示出了沿横截面的梯度大小，图5c示出了估计梯度的最小可靠尺度。请注意，随着信号强度的变化，估计范围如何自动适应。尽管这可以使该梯度在该横截面上可靠地检测为非零，但响应不是单峰的：实际上，沿边缘横截面的梯度有五个最大值。显然，选择梯度函数的最大值将导致对该单个边缘的多个单独响应。虽然没有单独基于梯度图的多重响应问题的本地解决方案，但在下一节中，我们将展示如何使用强度函数的二阶导数的可靠估计来解决该问题。

 

7 局部规模控制和第二微分估计

强度函数的二阶导数可以用高斯算子的可导二阶导数估算：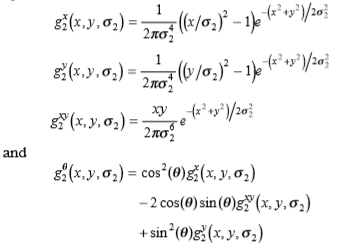

我们将注意力集中在沿梯度方向θ_M的强度函数的二阶导数上。由于是线性的，因此用于二阶导数估计的临界值函数c₂（σ₂）的推导相对简单。具体来说，我们要求

二阶导数算子的L₂范数由下式给出

代入并设置α_p = 2.0×10⁻⁷（第5节），我们有

其中s_n是噪声的标准偏差，而σ₂是二阶导数高斯滤波器的标度。

由于我们只对正交于边缘的亮度变化感兴趣，因此，在图像的每个点上，二阶导数都以最小可靠比例在估计的渐变方向上进行控制。二阶导数运算符对我们的本地边缘模型（1）的预期输出如下：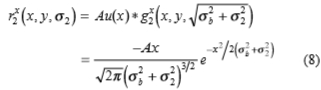

至于梯度，可以表明在边缘附近存在一个唯一的最小尺度，在该尺度上可以可靠地确定二阶导数的符号（第8节）。

因此获得了第二导数图，其在图像中可以估计出明显梯度的每个点处描述了该梯度如何沿梯度方向变化（如果有的话）。采用六个标度来估计八度间隔的二阶导数：σ₂∈{0.5，1，2，4，4，8，16}个像素。人体模型图像的最小可靠比例尺图如图4b所示。编码方案与梯度比例图相同。

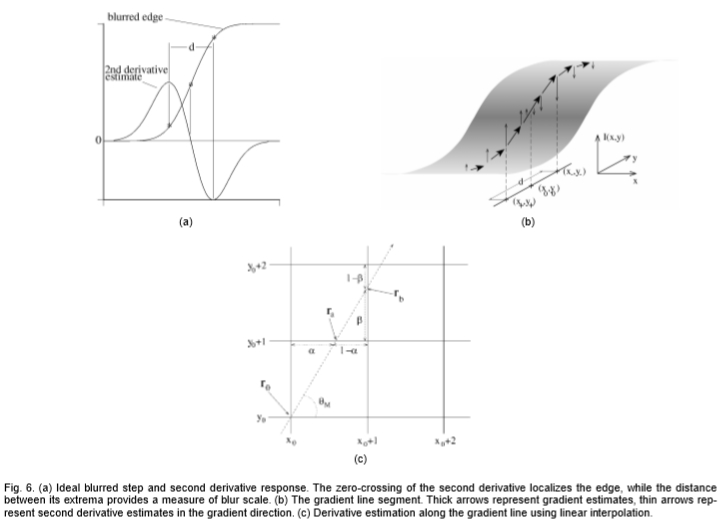
图6：（a）理想的模糊阶跃和二阶导数响应。 二阶导数的零交叉点使边缘局部化，而其极值之间的距离提供了模糊比例的度量。 （b）渐变线段。 粗箭头表示梯度估计，细箭头表示梯度方向上的二阶导数估计。 （c）使用线性插值法沿梯度线进行导数估计。

图6a示出了二阶导数如何区分边缘和平滑阴影梯度。二阶导数过零会在边缘上定位，而符号相反的侧面极值表示亮度函数的S型特征，从而将其与平滑阴影的坡度区分开。

图5说明了二阶导数在模糊边缘定位中的重要性。图5f显示了沿梯度方向操纵的估计二阶导数，图5e显示了这些估计的最小可靠标度。再次注意信号强度变化时刻度如何自动适应：在亮度函数几乎呈线性的边缘中心附近，需要更大的刻度。尽管梯度响应有些困难，但自适应二阶导数响应仍提供了一个独特的零交叉点来定位边缘。此处的关键在于，最小可靠范围的局部估计可确保二阶导数估计的正负号可靠，因此零交叉点是唯一的。另一方面，梯度响应中的峰数取决于边缘的模糊，并且在操作员的任何一点响应中都不会显示出来：确保梯度最大值的唯一性不是局部问题。因此，模糊边缘的可靠检测和定位需要梯度和二阶导数信息。

8 检测分析
 作为分析用于边缘检测的局部比例控制性能的第一步，我们可以使用（1）的边缘模型预测可检测到边缘的SNR和模糊比例的范围，以及所需的滤波器比例范围。为了检测边缘的S形，我们必须至少可靠地确定梯度在正负极值处的二阶导数的正负号，正负负值出现在模糊三阶导数的零交叉点x₊和x_- 处台阶边缘：

 

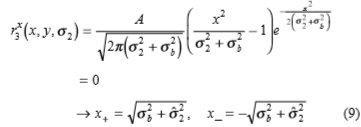
从（7）和（8），最小可靠的二阶导数标度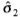必须满足：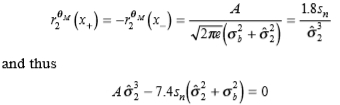

对于σ_b = 0的尖锐边缘，其减小为

为了在这些点上引导二阶导数，我们还必须可靠地检测信号的梯度。因此，从（4）和（5），我们得到最小可靠梯度标度：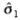

对于σ_b = 0的尖锐边缘，其减小为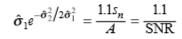

虽然在一般情况下我们无法解析地求解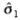和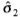，但我们可以使用迭代技术针对s_n，A和σ_b的特定值求解 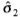，然后使用获得的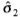求解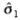。假设s_n = 1.6灰度级，我们针对不同幅度（A∈{1..32}灰度级：图3b）和低对比度边缘（σ_b∈{1..32}灰度级）的锐边（σ_b = 0）计算了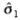和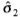。 A = 1灰度）在各种模糊（σ_b∈{1..32}像素：图3c）。注意，这些曲线代表检测边缘所需的最小比例尺。在下一部分中，我们将显示定位精度可能需要更高的二阶导数比例（另请参见[27]）。

 

 

9 本地化分析

在图5的示例中，阴影的对比度足够高，以允许可靠地估计沿梯度方向的每个像素处的二阶导数，从而可以在二阶导数中将边缘定位为零交叉。我们将这种边缘称为高精度边缘。对于非常低的对比度边缘，即使检测到第二导数极值，第二导数信号也可能太弱而无法可靠地确定零交叉附近的第二导数符号。因此，这些边缘在上一节的分析下可能是可检测的，但无法定位到一个像素的精度。我们将这些边缘称为低精度边缘。

要了解此定位问题，我们必须考虑零交叉附近的二阶导数响应的可靠性准则。根据（7）和（8），将e定义为实际边缘位置与可以可靠确定二阶导数的最近点之间的距离（以像素为单位），我们可以这样写：
 
对于 <<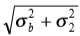，我们可以为（10）的左侧建立围绕 = 0的一阶泰勒级数，以得出的近似解

请注意，随着最大二阶导数滤波器比例的增加，精度会单调提高。当σ₂→∞时，精度渐近地接近 = 4.5 / SNR像素。

从理论上讲，定位精度不受边缘模糊的影响，而仅受边缘相对于传感器噪声的对比度的影响。为了获得最接近像素的精度，我们需要 <0.5，因此需要 SNR> 9.0。对于实际系统，必须在滤波器标度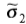上有一个上限，因此，为了获得最接近像素的精度，我们要求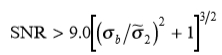

对于给定的最大滤镜比例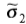，该方程式定义了一个对比度和边缘模糊范围，该范围可以定位到一个像素精度。图3d显示了我们实现的边界，其中我们使用的第二阶导数比例最大为σ₂ = 16像素。如果要将特定模糊比例σ_b的边缘定位到最近的像素，则SNR（A / s_n）必须保持在该曲线上方。

当检测到边缘但无法定位到一个像素精度时，应如何在边缘图中表示它们？在我们的实现中，我们用像素表示低精度边缘的位置，这些像素大致将连接第二阶导数响应的正负极值的梯度线段一分为二。第11节详细介绍了用于检测和表示低和高精度边缘的精确算法。

 

10 在离散网格上的实现

虽然最初仅在离散像素位置进行导数估计，但是边缘检测需要在像素外位置沿潜在边缘点的梯度线进行导数估计。图6c示出了当在梯度方向上进行估计时如何实现这一点。使用线性插值在梯度线与像素网格的第一个交点处进行第一估计r_a，在这种情况下，在像素（x₀，y₀ +1）和（x₀ +1，y₀ +1）之间：r_a =（1 −α）r（x₀，y₀ +1）+αr（x₀ +1，y₀ +1）。下一个交点出现在像素（x₀ + 1，y₀ + 1）和（x₀ + 1，y₀ + 2）之间，因此下一个导数估计r_b 由r_b =（1-β）r（x₀ + 1，y₀ + 1）+βr（x₀ + 1，y₀ + 2）。以类似的方式沿着与梯度相反的方向沿着梯度线进行估算。

在下文中，我们将插值微分估计标识为和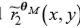，以与像素处的微分估计和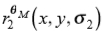区别开位置。我们不将比例尺与插值估算值相关联，因为它们可能是从以两种不同比例尺得出的像素上估算值得出的。

11 边缘标准概述

提出的边缘检测算法包括三个阶段：

1）使用局部比例控制可靠地估计每个图像点的强度梯度。

2）使用局部比例控制在每个图像点上可靠地估计强度函数在梯度方向上的二阶导数。

3）将边缘定位在梯度方向上二阶导数的零交叉处。虽然算法的基本结构很简单，但是离散实现以及在高精度和低精度情况下的处理都有一些细节，需要引起注意。我们将在接下来的两个小节中提供这些详细信息。

11.1 高精度边缘标准

要标记为高精度边缘，像素（x_p，y_p）必须位于强度函数的二阶导数的零交叉处。在梯度方向上通过（x_p，y_p）将（x_n，y_n）定义为像素网格与梯度线的第一个交点的位置，必须满足四个特定条件：

1）必须在以下点可靠地检测到梯度：对于某些σ₁。

2）必须在以下点可靠地将沿梯度方向的二阶导数检测为正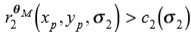：对于某些σ₂。

3）插值梯度必须在梯度方向上的下一个估计点处检测为非零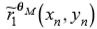：>0。

4）必须在梯度方向上的下一个估计点处将在梯度方向上插值的二阶导数检测为负值：<0。

在边缘的暗侧（二阶导数为正）表示边缘位置的选择是任意的。为了更精确地定位边缘，必须采用子像素表示[27]。

 

11.2 低精度边缘标准

要标记为低精度边缘，像素（x₀，y₀）必须与沿梯度线的二阶导数极值等距。这需要定义一个通过（x₀，y₀）的渐变线段（图6b）。

定义2.点（x₀，y₀）的梯度线段沿梯度方向延伸，直到检测到正的二阶导数估计，或者直到在负的估计值之后跟随一个不能可靠地估计二阶导数符号的点为止。被制造。类似地，梯度线段沿与梯度相反的方向延伸，直到检测到负的二阶导数估计，或者直到在正估计之后跟随不能做出二阶导数符号的可靠估计的点。我们将（x₊，y₊）定义为梯度线段上梯度方向上二阶导数的全局最大值的位置，将（x_-，y_-）定义为梯度中二阶导数的全局最小值的位置渐变线段上的方向。

给定此定义，如果像素（x₀，y₀）满足以下条件，则可以将其分类为低精度边缘：

1）在通过该点的渐变线段的所有网格交叉点处，可靠地将渐变检测为非零。

2）梯度线段至少有一个网格交点，在该交点处无法对梯度方向的二阶导数进行可靠估计。

3）在梯度方向上的梯度线段上存在可靠地检测到梯度方向上的二阶导数为负的点。

4）在梯度线段上与梯度相反的方向上存在一个点，其中可靠地检测到梯度方向上的二阶导数为正。

5）像素（x0，y0）位于将极值位置（x₊，y₊）和（x_-，y_-）一分为二的点的个像素内。

的公差说明了在将极值位置的平分表示为最接近的像素时出现的最坏情况的误差。

12 实验结果
12.1合成图像
1 2.1.1模糊比例实验

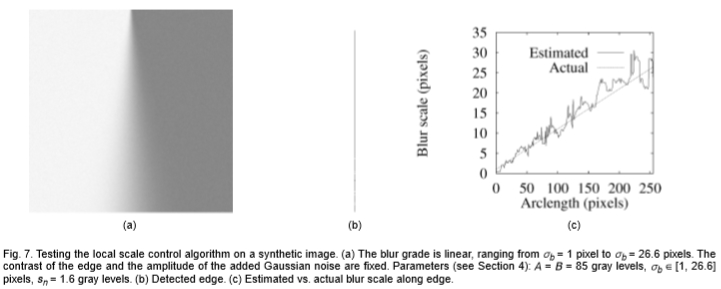
图7：在合成图像上测试局部比例控制算法。 （a）模糊等级是线性的，范围从σ_b = 1像素到σ_b = 26.6像素。 边缘的对比度和所加高斯噪声的幅度是固定的。 参数（请参见第4节）：A = B = 85个灰度级，σ_b∈[1，26.6]像素，s_n = 1.6灰度级。 （b）检测到的边缘。 （c）沿边缘的估计与实际模糊比例。

我们首先在图7a的合成图像上测试了边缘检测方法，该图像是由时空一维水平高斯模糊核模糊的垂直边缘，模糊比例沿该边缘线性增加。高斯i.d.添加了噪声（s_n = 1.6灰度级）以模拟传感器噪声。图7b示出了在该图像中检测到的边缘点。请注意，可以可靠地检测到边缘并将其定位在较大的模糊范围内，并且没有检测到人为边缘。

1 2.1.2 对比度（S N R）实验

 

图8：用于边缘定位的局部比例控制的SNR行为。 左列显示高斯噪声中一个正方形的合成图像。 从顶部到底部，SNR = 2、1、0.5。 中间的列显示了在估算强度函数在梯度方向上的二阶导数的符号时比例的变化。 较大的比例用浅灰色呈现，白色表示无法进行可靠的估计。 在这些噪声水平下，无法在任何规模下可靠地估算边缘附近的二阶导数的符号。 右列显示检测到的边缘。 高噪声水平下二阶导数的不确定性会导致定位误差。

为了评估作为噪声水平函数的局部比例控制算法的边缘检测性能，我们在高斯白噪声的正方形合成图像上运行了该算法（图8）。信噪比从上到下分别为2、1、0.5。在所有情况下，SNR都低于一个像素定位所需的范围（图3d）：因此，在这些合成图像中检测到的边缘为低精度边缘。

图8的中间一栏显示了比例图，用于估算每个点沿强度函数的梯度方向的二阶导数（比例尺越大，浅灰色，白色表示无法进行可靠的估算）。如预测的那样，在正方形边缘的紧邻处，二阶导数信号太弱而无法可靠地估计，因此二阶导数的显式零交叉不可用。右列显示了二阶导数信号中此丢失对边缘定位的影响。同样，没有检测到人为边缘。虽然在所有情况下都可以完全检测到平方，但是随着SNR的降低，边缘定位的误差会增加。人们还可以看到，随着SNR的降低，四角的圆角会增加。这是由于在较高的噪声水平下进行估计所需的较大比例的图像上的模糊增加。

12.2 自然图像

图4c示出了人体模型和阴影的图像中的边缘点的图。请注意，图像轮廓得以恢复，对人体模型后面以及阴影的前景和背景中的平滑阴影渐变没有虚假的响应。还应注意，人体模型的精细细节和阴影的完整轮廓都得到了解析（与图2中Canny / Deriche检测器的结果进行比较）。这是通过一个自动系统实现的，该系统除了传感器噪声的第二力矩外就没有任何输入参数。


希思等。最近，我们在一组自然图像上比较了五种边缘检测算法的性能。我们将确定由作者姓名测试的五种算法：Bergholm [11]，Canny [28]，Iverson和Zucker [29]，Nalwa和Binford [30]，以及Rothwell等。 [31]。在这项研究中，算法性能是根据主观人类视觉判断来评估的[32]。由于这些算法的性能取决于最多三个参数的设置，因此Heath等人。粗略地采样每种算法的参数空间，以确定每种算法的参数设置，以最大化所有图像的平均性能。除了Rothwell等人，其他所有研究都采用了具有滞后和非最大抑制的阈值[28]。探测器。

在他们的评估中，希思等人。对某些算法进行了更改，以便它们可以产生相同格式的输出以进行比较。对于Iverson和Zucker算法，这些更改非常重要，因此我们还包括了Iverson和Zucker算法原始版本的结果进行比较。

 

图9：局部比例控制与以前的边缘检测算法的比较。 （a）原始图像。 （b）通过局部比例控制检测到的边缘。 （c）伯格霍姆探测器[11]。 （d）Canny探测器[28]。 （e）艾弗森探测器[29]（由Heath等人[32]修改）。 （f）原始艾弗森探测器[29]（g）纳尔瓦探测器[30]。 （h）罗斯威尔探测器[31]。 （a），（c），（d），（e），（g）和（h）由南佛罗里达大学的K. Bowyer提供[32]。

Heath等人使用的测试图像之一。在图9a中示出。由局部比例控制算法计算的边缘图如图9b所示。由Bergholm，Canny，Iverson和Zucker（经修改），Iverson和Zucker（原始），Nalwa和Binford以及Rothwell等人计算的边缘图。算法显示在图1和2中。分别为9c，9d，9e，9f，9g和9h。

显然，与其他方法相比，局部比例控制算法如何检测到更多的低对比度，稍微模糊的叶子结构。虽然按照这个标准，最初的艾弗森和祖克检测器和纳尔瓦检测器是第二好的，但是检测到的许多叶片边缘都表现出第1节中讨论的多重响应问题。对于艾弗森和祖克检测器，这些轮廓看起来像是变厚或弄脏了。对于Nalwa探测器，它们表现为横向偏移的回波。

可能会争辩说，仅检测图像中一小部分边缘的方法可能有用，如果它们仅检测最重要的边缘而忽略了次要的边缘。但是，第2节的分析表明，在早期阶段进行这种区分非常困难，因为重要的边缘可能比相对不重要的边缘更模糊，对比度更低。因此，我们认为，边缘检测的目标应该是在出现对比度和模糊标度的广泛范围内检测图像中的所有边缘。当然，在将边缘图直接用于更高级别的任务（例如对象识别）之前，需要对边缘图进行后续处理。该更高级别的处理必须包括用于将纹理边缘与非纹理边缘区分开的方法[33]，以及将边缘分组为边界轮廓的方法（例如，[34]，[35]，[36]，[37]）。

13 局部比例控制以进行蓝色估计

 

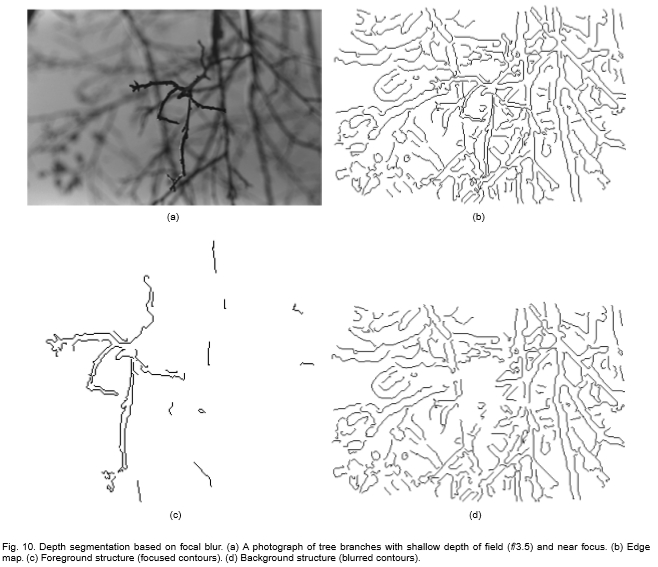
图10：基于焦点模糊的深度分割。 （a）景深浅（f /3.5）和近焦点的树枝照片。 （b）边缘贴图。 （c）前景结构（聚焦轮廓）。 （d）背景结构（轮廓模糊）。

图10显示了用浅景深（f / 3.5）拍摄的缠结的树枝。焦点集中在框架中央的相连的细枝簇形成清晰的主体，而其余分支则显示为散焦背景。图10b显示了使用局部比例控制对此图像检测到的边缘，以进行可靠的估计：聚焦和散焦分支均被恢复。注意，尽管遮挡为轮廓的深度排序提供了一些线索，但是丢失了由焦点模糊提供的前景和背景结构的即时感知分割。

 

现有的用于焦距模糊估计的技术通常假设表面深度变化缓慢[20]，[38]，[39]。对于该图像，该假设失败，在该图像中，任何局部邻域都可能包含许多不同的深度不连续点。这造成了一个难题：虽然使用较小的估计滤波器会由于传感器噪声而导致模糊估计的较大误差，但是使用较大的滤波器会由于图像附近但深度相距甚远的不同结构之间的干扰而增加误差（并且，因此，在对焦模糊中] [38]。因此，问题是选择一个折衷的滤波器标度，该标度应尽可能小，但要足够大，以避免传感器噪声引起的误差。本地比例控制自然适合此任务。

为了估计焦点模糊，我们的边缘模型的高斯核表示所用摄像机镜头系统的点扩散函数。根据（9），估计的二阶导数中的极值位置预计会出现在边缘位置两侧的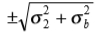像素处，其中σ₂是二阶导数算子的最小可靠尺度。边缘的模糊比例。将d 定义为梯度方向上相反符号的二阶导数极值之间的距离（图6a），我们得到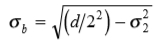


因此，在补偿由估计本身引起的模糊之后，可以根据所测量的轮廓厚度来估计由于散焦引起的模糊。

图7c示出了图7a的合成测试图像的估计和实际模糊的图。误差随模糊比例大致线性增加，因此最好用百分比表示。虽然估计方法似乎是无偏的，平均误差仅为2.8％，但单个估计却非常嘈杂，RMS误差为17.6％。虽然我们不知道用于评估单个图像中模糊性的竞争方法的性能指标（例如，与估计来自不同景深的两个图像的范围的误差相反），但对于人类视觉而言，边缘模糊性的明显差异已知该系统的数量级为13％至20％[40]，这意味着可以估计9％至14％的单个边缘的模糊。

我们认为，我们方法中错误的主要来源是边缘的二阶导数极值的定位错误。请注意，选择二阶导数滤波器的比例是为了确保可靠地检测到二阶导数的符号：这不能保证极值将正确定位，实际上，对于模糊边缘，通常会存在多个极值。该问题类似于使用梯度最大值来定位边的位置的问题（请参见第7节）。正确的解决方案也类似：要定位边缘，我们必须可靠地检测梯度方向上的二阶导数的零交叉，要定位二阶导数极值（并因此估计模糊度），我们必须可靠地检测三阶导数的零交叉。梯度方向的导数。我们目前正在基于这种局部比例控制技术开发一种改进的模糊估计方法。

尽管在本发明的用于模糊估计的方法中存在噪声，但是仍然可以有效地将其用于将图像结构分割成不同的深度平面。例如，我们可以将其应用于图10的图像，以复制在查看原始图像时遇到的主题和背景之间的感知分割。图10c和10d分别显示了提取的前景（聚焦）和背景（散焦）结构。

 

14 来自DEFOCUS和CAST SHADOWS的空间曲线

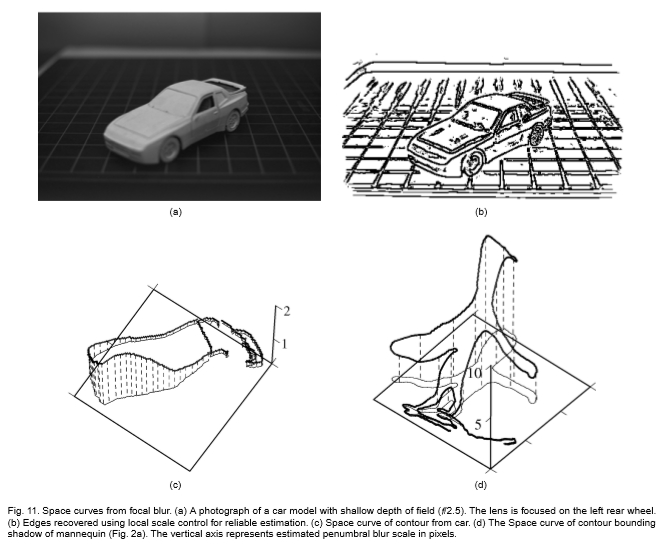
图11：焦点模糊产生的空间曲线。 （a）景深浅的汽车模型照片（f /2.5）。 镜头聚焦在左后轮上。 （b）使用局部比例控制来恢复边缘以进行可靠的估计。 （c）汽车轮廓线的空间曲线。 （d）人体轮廓轮廓阴影的空间曲线（图2a）。 垂直轴表示以像素为单位的估计半影模糊度。

虽然其他人已经成功地将轮廓分类为细的或弥散的[41]，[42]，[43]，但我们在这里表明，我们的轮廓模糊估计方法可以沿图像轮廓连续提供密集的估计，以从图像中恢复完整的空间曲线。图片。例如，考虑用浅景深（f / 2.5）拍摄的模型车的图像（图11a）。镜头聚焦在汽车的后轮上，因此发动机罩和前保险杠散焦了。图11b示出了通过最小可靠比例法选择的边缘。请注意，尽管严重散焦，仍可以可靠地检测和定位前景和背景结构。图11c示出了汽车的主要轮廓之一的三维图。此处的垂直轴表示聚焦模糊σ_b，如上一节所述进行估算，并使用高斯模糊核（σ= 22像素）沿轮廓平滑。该轮廓提供了对焦点模糊的连续估计，该焦点模糊与单调函数相关，它与距最佳聚焦平面的距离有关，在这种情况下，该距离位于模型车的后轮。

这种用于模糊估计的方法也可以用于估计半影模糊。让我们再次考虑人体模型投射阴影的图像（图2a）。阴影轮廓的模糊朝向阴影的头部增加。沿阴影轮廓线的半影模糊估计的结果（沿轮廓线的高斯平滑模糊估计后，σ= 22像素）如图11d所示。

如第1节所述，散焦和投射阴影之间的对偶性表明，无法通过对单个图像帧进行局部计算来区分聚焦和半影模糊。现有的用于估计散焦深度的被动方法通常使用两个具有不同景深的帧来将焦点模糊与其他类型的模糊区分开来[20]，[38]，[39]。该技术也可以应用到我们的模糊估计方法中，从而可以分别分离和估计焦点和半影模糊。

 

15 悬而未决的问题和未来的工作

我们可以通过多种方式扩展或计划扩展当前的工作：

1）使用局部比例控制对边缘点进行亚像素定位。初步结果已有报道[27]。

2）扩展比例适应，包括方向调整适应，从而可以可靠地检测出非常低的SNR和杂乱的边缘。

3）基于使用局部比例控制对三阶导数的可靠估计，提高了模糊估计的精度。

一个主要的开放问题是我们如何最好地评估我们的边缘模型和建议的局部比例控制方法在多大程度上准确地代表自然图像中的所有边缘。为了解决这个问题，我们最近开发了一种用于反转边缘表示以计算原始图像估计值的方法[27]。每个边缘点由（1）的参数表示。从该表示，我们表明可以计算出原始图像的估计，其在感知上几乎与原始图像相同。发现模型的模糊比例分量对于实现感知上准确的重建至关重要。这些结果表明，所提出的模型和边缘检测方法实际上可以准确表示图像的所有边缘。

这项工作面临的最困难的开放问题可能是假设的有效性，即每个边缘点只有一个比例就足以表征图像。考虑例如阴影落在带纹理的表面上。在阴影的许多点上，我们可能希望在两个不同的方向和比例上确定两个边缘：由纹理元素生成的小比例边缘和由软阴影生成的大比例边缘。在这种情况下，我们可能希望在每个边缘点上搜索比例和方向空间，以寻找该点上可能存在的多个边缘。对于这种算法，由局部比例控制选择的比例将仅形成比例空间中的下包络，在该范围内必须限制此搜索。此方法的替代方法是通过“二次”计算来检测这种阴影边缘，该“二次”计算可检测先前检测到的纹理边缘的强度统计数据中的突然变化。
 
16 结论

由于未知的模糊比例和对比度的模糊亮度转换，世界上的物理边缘通常会投射到视觉图像上。在如此广泛的条件下检测，定位和表征边缘需要多尺度方法。先前使用局部尺度选择进行边缘检测的尝试未能将真实边缘与人为边缘区分开来和/或需要启发式全局计算。在本文中，我们已经表明，只要对传感器噪声和操作员规范具有先验知识，就可以使用纯局部计算可靠地将真实边缘与人为边缘区分开。所提出的用于局部比例控制的算法可以在很大范围的模糊比例和对比度上检测和定位边缘，并且除了传感器噪声的第二矩外，不需要任何输入参数。这种用于边缘检测的方法自然导致了一种用于估计图像轮廓的局部模糊的方法。这种基于轮廓的模糊估计方法对于复杂图像很有用，在复杂图像中，基于傅立叶模糊估计方法的平滑度假设不适用。

致谢

这项工作得到了加拿大自然科学与工程研究理事会和美国空军科学研究所的支持。我们感谢迈克尔·兰格（Michael Langer）和三位匿名审稿人，他们的评论大大改善了该手稿。

 

参考文献

[1]  J. Canny, “Finding Edges and Lines in Images,” Master’s thesis, MIT Artificial Intelligence Laboratory, 1983.
[2]  R. Deriche, “Using Canny’s Criteria to Derive a Recursively Implemented Optimal Edge Detector,” Int’l J. Computer Vision, vol. 1, no. 2, pp. 167-187, 1987.
[3]  A. Blake and A. Zisserman, Visual Reconstruction. Cambridge, Mass.: MIT Press, 1987.
[4]  Y. Leclerc and S. Zucker, “The Local Structure of Image Discontinuities in One Dimension,” IEEE Trans. Pattern Anaysis and Machine Intelligence, vol. 9, no. 3, pp. 341-355, 1987.
[5]  J. Elder, The Visual Computation of Bounding Contours. PhD thesis, McGill University, Dept. of Electrical Eng., 1995.
[6]  D. Hubel and T. Wiesel, “Receptive Fields and Functional Architecture in the Cat’s Visual Cortex,” J. Neuroscience, vol. 160, pp. 106-154, 1962.
[7]  D. Hubel and T. Wiesel, “Receptive Fields and Functional Architecture of Monkey Striate Cortex,” J. Neuroscience, vol. 195, pp. 215-243, 1968.
[8]  D. Marr and E. Hildreth, “Theory of Edge Detection,” Proc. Royal Soc. of London B, vol. 207, pp. 187-217, 1980.
[9]  A. Witkin, “Scale Space Filtering,” Proc. Int’l Joint Conf. Artificial Intelligence, pp. 1,019-1,021, Karlsruhe, 1983.
[10] J. Koenderink, “The Structure of Images,” Biol. Cyberetics, vol. 50, pp. 363-370, 1984.
[11]  F. Bergholm, “Edge Focusing,” IEEE Trans. Pattern Analysis and Machine Intelligence, vol. 9, no. 6, pp. 726-741, 1987.
[12]  T. Lindeberg, “Scale-Space for Discrete Signals,” IEEE Trans. Pattern Analysis and Machine Intelligence, vol. 12, no. 3, pp. 234-254, 1990.
[13]  Y. Lu and R. Jain, “Reasoning About Edges in Scale Space,” IEEE Trans. Pattern Analysis and Machine Intelligence, vol. 14, no. 4, pp. 450–468, 1992.
[14]  P. Perona and J. Malik, “Scale-Space and Edge Detection Using Anisotropic Diffusion,” IEEE Trans. Pattern Analysis and Machine Intelligence, vol. 12, pp. 629-639, 1990.

[15]  T. Lindeberg, “Detecting Salient Blob-Like Image Structures and Their Scales With a Scale-Space Primal Sketch: A Method for Focus-of-Attention,” Int’l J. Computer Vision, vol. 11, no. 3, pp. 283318, 1993.
[16]  H. Jeong and C. Kim, “Adaptive Determination of Filter Scales for Edge Detection,” IEEE Trans. Pattern Analysis and Machine Intelligence, vol. 14, no. 5, pp. 579-585, 1992.
[17]  T. Lindeberg, Scale-Space Theory in Computer Vision. Dordrecht, The Netherlands: Kluwer, 1994.
[18]  T. Lindeberg, “Edge Detection and Ridge Detection With Automatic Scale Selection,” IEEE Conf. Computer Vision Pattern Recognition, pp. 465-470, San Francisco, IEEE CS Press, June 1996.
[19]  G. Healey and R. Kondepudy, “Modeling and Calibrating CCD Cameras for Illumination Insensitive Machine Vision,” PhysicsBased Vision: Radiometry, L. Wolff, S. Shafer, and G. Healey, eds. Boston, Mass.: Jones and Bartlett, 1992.
[20]  A. Pentland, “A New Sense for Depth of Field,” IEEE Trans. Pattern Analysis and Machine Intelligence, vol. 9, no. 4, pp. 523-531, 1987.
[21]  M. Subbarao, “Parallel Depth Recovery by Changing Camera Parameters,” Proc. Second Int’l Conf. Computer Vision, pp. 149-155, Tampa, Fla., IEEE CS Press, 1988.
[22]  A. Pentland, S. Scherock, T. Darrell, and B. Girod, “Simple Range Cameras Based on Focal Error,” J. Optical Soc. Am. A, vol. 11, no. 11, pp. 2,925-2,934, 1994.
[23]  A. Papoulis, Probability, Random Variables and Stochastic Processes. New York, NY: McGraw-Hill, 1965.
[24]  W. Freeman and E. Adelson, “The Design and Use of Steerable Filters,” IEEE Trans. Pattern Analysis and Machine Intelligence, vol. 13, no. 9, pp. 891-906, 1991.
[25]  P. Perona, “Deformable Kernels for Early Vision,” IEEE Trans. Pattern Analysis and Machine Intelligence, vol. 17, no. 5, pp. 488-499, 1995.
[26]  E. Wong, Introduction to Random Processes. New York: SpringerVerlag, 1983.
[27]  J. Elder and S. Zucker, “Scale Space Localization, Blur and Contour-Based Image Coding,” Proc. IEEE Conf. Computer Vision Pattern Recognition, pp. 27-34, San Francisco, IEEE CS Press, 1996.
[28]  J. Canny, “A Computational Approach to Edge Detection,” IEEE Trans. Pattern Analysis and Machine Intelligence, vol. 8, no. 11, pp. 679-698, Nov. 1986.
[29]  L. Iverson and S. Zucker, “Logical/Linear Operators for Image Curves,” IEEE Trans. Pattern Analysis and Machine Intelligence, vol. 17, no. 10, pp. 982-996, Oct. 1995.
[30]  V. Nalwa and T. Binford, “On Detecting Edges,” IEEE Trans. Pattern Analysis and Machine Intelligence, vol. 8, no. 6, pp. 699-714, 1986.
[31]  C. Rothwell, J. Mundy, W. Hoffman, and V. Nguyen, “Driving Vision by Topology,” Int’l Symp. Computer Vision, pp. 395-400, Coral Gables, Fla., Nov. 1995.
[32]  M. Heath, “A Robust Visual Method for Assessing the Relative Performance of Edge Detection Algorithms,” Master’s thesis, Univ. of South Florida, Dec. 1996.
[33]  M. Heath, S. Sarkar, T. Sanocki, and K. Bowyer, “Comparison of Edge Detectors: A Methodology and Initial Study,” Proc. IEEE Conf. Computer Vision Pattern Recognition, pp. 143-148, San Francisco, IEEE CS Press, June 1996.
[34]  B. Dubuc and S. Zucker, “Indexing Visual Representations Through the Complexity Map,” Proc. Fifth Int’l Conf. Computer Vision, pp. 142-149, Cambridge, Mass., June 1995.
[35]  I. Cox, J. Rehg, and S. Hingorani, “A Bayesian MultipleHypothesis Approach to Edge Grouping and Contour Segmentation,” Int’l J. Comp. Vision, vol. 11, no. 1, pp. 5-24, 1993.
[36]  J. Elder and S. Zucker, “Computing Contour Closure,” Lecture Notes in Computer Science, Proc. Fourth European Conf. on Computer Vision, pp. 399-412, New York, NY, Springer Verlag, 1996.
[37]  D. Jacobs, “Finding Salient Convex Groups,” Partitioning Data Sets DIMACS (Series in Discrete Mathematics and Theoretical Computer Science), I. Cox, P. Hansen, and B. Julesz, eds., vol. 19, 1995.
[38]  D. Lowe, “Three-Dimensional Object Recognition From Single Two-Dimensional Images,” Artificial Intelligence, vol. 31, pp. 355395, 1987.
[39]  J. Ens and P. Lawrence, “Investigation of Methods for Determining Depth From Focus,” IEEE Trans. Pattern Analysis and Machine Intell., vol. 15, no. 2, pp. 97-108, 1993.