Image Processing and Analysis_8_Edge Detection：A Computational Approach to Edge Detection——1986

此主要讨论图像处理与分析。虽然计算机视觉部分的有些内容比如特 征提取等也可以归结到图像分析中来，但鉴于它们与计算机视觉的紧密联系，以 及它们的出处，没有把它们纳入到图像处理与分析中来。同样，这里面也有一些 也可以划归到计算机视觉中去。这都不重要，只要知道有这么个方法，能为自己 所用，或者从中得到灵感，这就够了。

8. Edge Detection
边缘检测也是图像处理中的一个基本任务。传统的边缘检测方法有基于梯度 算子，尤其是 Sobel 算子，以及经典的 Canny 边缘检测。到现在，Canny 边缘检 测及其思想仍在广泛使用。关于 Canny 算法的具体细节可以在 Sonka 的书以及 canny 自己的论文中找到，网上也可以搜到。最快最直接的方法就是看 OpenCV 的源代码，非常好懂。在边缘检测方面，Berkeley 的大牛 J Malik 和他的学生 在 2004 年的 PAMI 提出的方法效果非常好，当然也比较复杂。在复杂度要求不高 的情况下，还是值得一试的。MIT的Bill Freeman早期的代表作Steerable Filter 在边缘检测方面效果也非常好，并且便于实现。这里给出了几篇比较好的文献， 包括一篇最新的综述。边缘检测是图像处理和计算机视觉中任何方向都无法逃避 的一个问题，这方面研究多深都不为过。
[1980] theory of edge detection
[1983 Canny Thesis] find edge
[1986 PAMI] A Computational Approach to Edge Detection
[1990 PAMI] Scale-space and edge detection using anisotropic diffusion
[1991 PAMI] The design and use of steerable filters
[1995 PR] Multiresolution edge detection techniques
[1996 TIP] Optimal edge detection in two-dimensional images
[1998 PAMI] Local Scale Control for Edge Detection and Blur Estimation
[2003 PAMI] Statistical edge detection_ learning and evaluating edge cues
[2004 IEEE] Edge Detection Revisited
[2004 PAMI] Design of steerable filters for feature detection using canny-like criteria
[2004 PAMI] Learning to Detect Natural Image Boundaries Using Local Brightness, Color, and Texture Cues
[2011 IVC] Edge and line oriented contour detection State of the art

 

翻译

边缘检测的计算方法——http://tongtianta.site/upload

作者：John Canny

 

摘要 -本文介绍了一种边缘检测的计算方法。该方法的成功取决于用于计算边缘点的一组全面目标的定义。这些目标必须足够精确，以界定检测器的所需行为，同时对解决方案的形式做出最小假设。我们为一类边缘定义了检测和定位标准，并针对这些标准提出了数学形式，作为运算符脉冲响应上的函数。然后添加第三标准，以确保检测器对单个边缘仅具有一个响应。我们使用数值优化中的标准来导出几个常见图像特征（包括台阶边缘）的检测器。通过对台阶边缘进行专门分析，我们发现在检测和定位性能之间存在自然的不确定性原理，这是两个主要目标。利用这一原理，我们得出了在任何规模下均最佳的单一操作符形状。最佳检测器具有一个简单的近似实现方式，其中边缘以高斯平滑图像的梯度幅度最大值标记。我们使用几个宽度的运算符扩展了这个简单的检测器，以应对图像中不同的信噪比。我们提出了一种通用的方法，称为特征合成，用于对来自不同规模运营商的信息进行精细到粗略的集成。最终，我们表明，随着操作员点扩展函数沿边缘扩展，阶跃边缘检测器的性能大大提高。该检测方案在每个点使用几个拉长的算子，并且方向算子输出与最大梯度检测器集成在一起。

索引—边缘检测，特征提取，图像处理，机器视觉，多尺度图像分析。

 

Ⅰ 引言
某些类型的边缘检测器，尤其是阶梯边缘检测器，已经成为许多计算机视觉系统的重要组成部分。边缘检测过程通过大大减少要处理的数据量来简化图像分析，同时保留有关对象边界的有用结构信息。边缘检测的应用程序中当然有很多多样性，但是可以感觉到许多应用程序都具有一组共同的要求。这些要求产生了一个抽象的边缘检测问题，可以将其解决方案应用于任何原始问题域中。

我们应该在这里提到一些特定的应用程序。 Binford-Horn寻线器[14]使用边缘检测器的输出作为程序的输入，该程序可以隔离简单的几何实体。最近，基于模型的视觉系统ACRONYM [3]使用边缘检测器作为复杂识别程序的前端。运动[29]，[13]的形状可用于根据图像轮廓中边缘轮廓或边缘点的运动来推断三维对象的结构。几种现代的立体视理论假设图像在匹配完成之前由边缘检测器进行了预处理[19]，[20]。 Beattie [1]描述了一种基于边缘的标记方案，用于低级图像理解。最后，提出了一些新颖的方法来从图像轮廓中提取三维信息，即轮廓[27]的形状和纹理[31]的形状。

在所有这些示例中，都有与边缘检测器性能相关的通用标准。第一个也是最明显的是低错误率。重要的是，不要错过图像中出现的边缘，并且没有虚假的响应。在上述所有情况下，边缘检测器错误都会影响系统性能。第二个标准是边缘点定位良好。也就是说，检测器标记的点与真实边缘的“中心”之间的距离应最小化。对于运动产生的立体感和形状尤其如此，其中在左右图像之间或在稍有不同的时间产生的图像之间测量出小的差异。

 

在本文中，我们将针对这两个标准开发一种数学形式，可用于设计任意边缘的检测器。我们还将发现前两个标准不够“严格”，并且有必要添加第三个标准来规避对单个边缘的多个响应的可能性。通过数值优化，我们得出了山脊和屋顶边缘的最优算子。然后，我们将专门针对台阶边缘的标准，并给出解决方案的参数封闭形式。在此过程中，我们将发现存在一个不确定原理，该原理涉及到噪声阶跃边缘的检测和定位，并且两者之间存在直接的权衡。这种关系的一个结果是，对于最佳阶梯边缘检测器而言，脉冲响应只有一个唯一的“形状”，并且可以通过改变检测器的空间宽度来改变检测与定位之间的权衡。将给出检测器在真实图像上的性能的几个示例。

 II 一维公式
为了便于分析，我们首先考虑一维边缘轮廓。也就是说，我们将假定二维边缘在某个方向上局部具有恒定的横截面。例如，对于光滑的边缘轮廓或山脊将是正确的，但对于拐角则不是这样。我们将假定图像由边缘和加性高斯白噪声组成。

 

图1：（a）嘈杂的台阶边缘。 （b）装箱员的区别。 （c）应用于边缘的盒子算子的区别。 （d）高斯算子的一阶导数。 （e）应用到边缘的高斯一阶导数。

 

检测问题的公式如下：我们首先从已知横截面的边缘浸入高斯白噪声中，如图1（a）所示，它显示了阶跃边缘。 我们用一个滤波器进行卷积，该滤波器的脉冲响应可以用图1（b）或（d）来说明。 卷积的输出分别在图1（c）和（e）中示出。 我们将在卷积的输出中将边的中心标记为局部最大值。 这样，设计问题就变成了一种滤波器，该滤波器相对于以下给出的标准给出了最佳性能。 例如，在该示例上，图1（d）中的滤波器的性能比图1（b）好得多，因为后者的响应在边缘区域表现出几个局部最大值。

 

总之，三个性能标准如下：

1）良好的检测。 无法标记真实边缘点的可能性较低，而错误标记非边缘点的可能性较低。 由于这两个概率都是输出信噪比的单调递减函数，因此该标准对应于最大化信噪比。

2）良好的本地化。 操作员标记为边缘点的点应尽可能靠近真实边缘的中心。

3）对单个边缘只有一个响应。 这是在第一个标准中隐式捕获的，因为当对同一边有两个响应时，必须将其中一个视为错误。 但是，第一个准则的数学形式并未满足多重响应要求，因此必须明确。

 

A.检测和定位标准
我们方法的关键步骤是以易于解决的数学形式捕获上面给出的直观标准。我们首先处理信噪比和定位。令滤波器的脉冲响应为f（x），并用G（x）表示边缘本身。我们将假设边缘以x = 0为中心。然后，通过卷积积分，滤波器对该边缘在其中心H_G 的响应：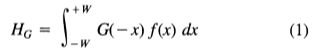

假设滤波器具有以[-W，W]为边界的有限脉冲响应。仅对噪声n（x）的均方根响应为

其中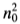是每单位长度的均方根噪声幅度。我们定义我们的第一个标准，即输出信噪比，作为这两个响应的商。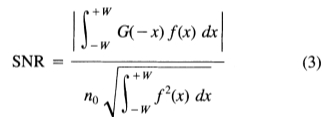

对于定位标准，我们需要一些随定位提高而增加的度量，并且将使用标记边缘到真实边缘中心的均方根距离的倒数。由于我们决定在算子f（x）的响应中标记局部最大值处的边缘，因此响应的一阶导数在这些点处将为零。还要注意，由于边缘的中心位于x = 0，所以在没有噪声的情况下，x =0 时响应中应该有一个局部最大值。

令H_n（x）仅是滤波器对噪声的响应，而H_G（x）是其对边缘的响应，并假设总响应在x = x₀ 处有一个局部最大值。那我们有

 

H‘_G（x₀）关于原点的泰勒展开式给出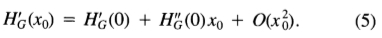

通过假设H'_G（0）= 0，即在无噪声的情况下滤波器的响应在原点处具有局部最大值，因此可以忽略扩展中的第一项。假定实际最大值的位移x₀小，因此我们将忽略二次项和更高项。实际上，通过一个简单的论点我们可以证明，如果边G（x）是对称的或反对称的，则x₀中的所有偶数项都将消失。假设G（x）是反对称的，并且将f（x）表示为对称分量和反对称分量的总和。对称分量与G（x）的卷积对SNR的分子没有任何贡献，但对分母中的噪声分量有任何贡献。因此，如果f（x）具有任何对称分量，则其SNR将比纯反对称滤波器差。对偶参数适用于对称边，因此，如果边G（x）是对称的或反对称的，则过滤 f（x）也会成立。这样做的最终结果是，响应H_G（x）始终是对称的，并且其奇数阶的导数 [出现在（5）中的偶数阶的系数中] 在原点为零。等式（4）和（5）给出

现在H'_n（x₀）是一个高斯随机量，其方差是H'_n（x₀）的均方值，由下式给出：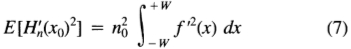

其中E [y]是y的期望值。将此结果与（6）组合，并替换H"_G（0）得到

其中是x₀的标准偏差的近似值。本地化定义为的倒数。

公式（3）和（9）是前两个准则的数学形式，并且设计问题同时减少到这两个准则的最大化。为此，我们将（3）和（9）的乘积最大化。可以想象，我们可以使用两个参数中任何单调的函数来组合（3）和（9），但是乘积的使用简化了阶跃边缘的分析，这在第三节中应该很清楚。目前，我们将利用任意边缘标准的乘积，即我们寻求最大化

解决方案上可能存在一些其他约束，例如下面描述的多重响应约束（12）。

 

B.消除多重响应

在我们对边缘检测问题的规范中，我们决定在应用于图像的线性滤波器的响应中，将边缘标记在局部最大值处。最后一部分给出的检测标准衡量了滤波器在区分边缘中心信号和噪声方面的有效性。它没有考虑边缘中心附近的滤镜行为。前两个标准可以按如下方式简单地最大化。从积分的Schwarz不等式，我们可以证明SNR（3）的上界为

和本地化（9）

当[-W, W] 中的 f（x）= G（-x）时，可以达到两个边界，并且SNR和定位的乘积最大。

 

因此，根据前两个标准，梯级边缘的最佳检测器是截断的梯级或箱差运算符。 Rosenfeld和Thurston [25]使用了盒子的差异，Herskovits和Binford [11]则使用了横向抑制。然而，它具有非常高的带宽，并且在对嘈杂的台阶边缘的响应中往往表现出许多最大值，这在成像系统添加噪声或图像本身包含纹理化区域时是一个严重的问题。根据我们的第一个标准，这些额外的边缘应被认为是错误的。但是，此标准的分析形式是从单个点（边缘的中心）处的响应派生的，并且没有考虑附近几个点处的响应的交互作用。如果检查盒子边缘检测器差异的输出，我们会发现对噪声阶跃的响应是一个近似三角形的峰值，在边缘附近有许多尖锐的最大值（见图1）。

这些最大值非常接近，以致于无法选择一个作为对步骤的响应，而将其他识别为噪声。我们需要向我们的标准添加要求，即函数f对阶跃附近的单个阶跃边不会有“太多”的响应。我们需要限制响应中的峰值数量，以便声明多个边的可能性很小。理想情况下，我们希望使噪声响应中的峰之间的距离近似于操作员对单个步骤的响应的宽度。该宽度将是运算符宽度W的一部分。

 

为了将其表示为对 f 的功能约束，我们需要获得相邻噪声峰之间距离的表达式。我们首先注意到输出中相邻最大值之间的平均距离是算子输出导数中相邻零交叉之间距离的两倍。然后，我们利用赖斯[24]的结果得出，函数g 对高斯噪声的响应的零交叉点之间的平均距离为

其中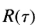是g的自相关函数。在我们的案例中，我们正在寻找函数f' 的平均零交叉间距。现在，因为

f' 过零距离之间的平均距离为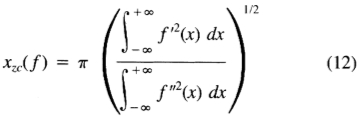

噪声响应关闭中相邻最大值之间的距离表示为X_max，将是x_zc的两倍。我们将此距离设置为操作员宽度的几分之一k。

 

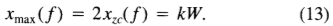
这是约束的自然形式，因为滤波器的响应将集中在宽度为2 W的区域中，并且该区域中的预期噪声最大值为N_n，其中

固定k固定可能导致错误响应的最大噪声数量。我们在此指出，最大间距（12）与操作符宽度成比例。也就是说，我们首先定义一个算子f_w，它是将f拉伸w的结果，f_w（x）= f（x|w）。然后代入（12）后，我们发现f_w 的最大间隔为x_zc(f_w)= wx_zc(f)。因此，如果函数f_w 满足固定k的多重响应约束（13），则假定W随w缩放，函数f_w也将满足它。对于任何固定的k，多重响应准则相对于f 的空间缩放都是不变的。

III 通过数值优化找到最佳探测器

通常，很难（或不可能）找到函数的闭合形式，该形式在多重响应约束下最大化（10）。 即使当G具有特别简单的形式（例如，它是台阶边缘）时，形式也可能很复杂。 但是，如果给定候选函数f，则对（10）和（12）的求值很简单。 特别是，如果函数f由离散的时间序列表示，则对（10）的求值仅需要计算序列之间的四个内积。 这表明可以直接对采样的算子脉冲响应进行数值优化。

 

对于操作员而言，输出将不是解析形式，但是无论如何，实现针对感兴趣边缘的检测器将需要离散的点扩展函数。通过使用惩罚方法[15]，也可能包括其他约束。在这种方案中，约束优化被简化为一个或可能多个无约束的优化。对于每个约束，我们定义一个惩罚函数，当违反其中一个约束时，惩罚函数的值将为非零。然后我们找到最大的f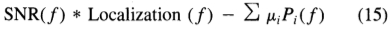

其中P_i 是仅当违反约束时才具有正值的函数。u_i 的值越大，越能满足约束条件，但是同时，问题变得更糟的可能性也越大。可能需要使用值u_i的序列，其最终形式与每次优化时所用的形式不同，都是下一个优化的起始形式。 在每次迭代中增加u_i，以使P_i（f）的值减小，直到“几乎”满足约束条件为止。

 

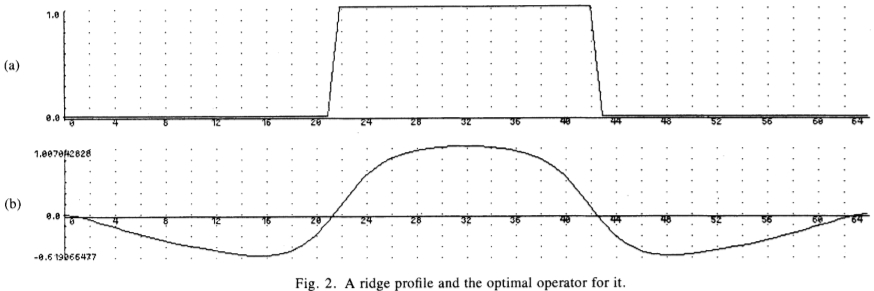
图2：山脊轮廓及其最佳算子。

图2中显示了应用于检测“山脊”轮廓问题的方法的一个示例。对于山脊，函数G定义为宽度为w的平坦平台，两端的步长过渡为零。辅助约束是：

*多重响应约束。该约束直接取自（12），并且不取决于边缘的形式。
*操作员的直流分量应为零。也就是说，它应具有零输出到恒定输入。

由于操作员的宽度取决于脊的宽度，因此建议应使用多个宽度的操作员。然而，这在本实施方式中并未完成。宽的脊可以被认为是两个紧密间隔的边缘，并且实施方案已经包括用于这些边缘的检测器。使用脊线检测器的唯一原因是图像中的脊线太小而无法由最窄的边缘算子有效处理。由于存在许多边缘（例如划痕，裂缝或印刷品），其边缘处于或超出相机的分辨率，导致轮廓仅宽一个或两个像素，因此经常发生这种情况。

图3：屋顶轮廓和屋顶的最佳操作员。

使用类似的过程找到屋顶边缘的最佳算子。这些边缘通常出现在多面体对象中两个平面的凹面连接处。结果如图3所示。再次有两个辅助约束，一个是对多个输入的响应，另一个是对恒定输入的零响应。

屋顶边缘检测器没有被并入边缘检测器的实现中，因为发现理想的屋顶边缘相对很少。在任何情况下，脊形检测器都是理想的屋顶检测器的近似值，足以应付屋顶。对于专门设计用于处理多面体图像的边缘检测器，例如Binford-Horn寻线器[14]，情况可能有所不同。

刚刚描述的方法已被用来找到脊和屋顶轮廓的最优算子，此外，它成功地找到了第四节中推导的最优阶梯边缘算子。应该可以使用它来查找任意一维边缘的算子，并且应该可以在二维中应用该方法以找到针对各种类型拐角的最佳检测器。

 

IV 台阶式探测器
现在，我们将最后一部分的结果专用于输入G（x）是阶跃边的情况。具体来说，我们设置G(x)=Au_-1(x)，其中，u_n(x) 是delta函数的n次导数，A是步幅。就是说，

并用（3）和（9）中的G（x）代替

这两个标准都直接用比率A/n₀ 改善，该比率可以称为图像的信噪比。现在，我们消除对图像的依赖，并定义两个性能指标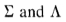，它们仅取决于滤镜：

现在假设我们从f组成一个空间缩放的滤波器f_w，其中 f_w(x)= f(x|w) 。回顾第二节末尾，多重响应标准不受空间缩放的影响。当将f_w代入（19）和（20）时，我们就不喜欢缩放滤波器的性能：

这些方程式中的第一个是非常直观的，并且意味着当应用于阶跃边缘时，具有较宽脉冲响应的滤波器将比较窄滤波器具有更好的信噪比。第二个不太明显，这意味着较窄的滤镜比宽的滤镜具有更好的定位效果。令人惊讶的是，这些变化是成反比的，也就是说，两个标准都以增大或减小。存在不确定性原理，与台阶边缘检测器的检测和定位性能有关。通过f的空间缩放，我们可以权衡检测性能与定位，但不能同时提高两者。这表明复合准则的自然选择将是（19）和（20）的乘积。因为该乘积在尺度变化下将是不变的。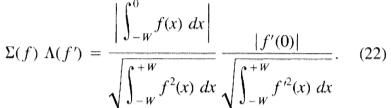

 该表达式最大化的解决方案将是一类与空间缩放相关的函数。实际上，该结果与标准组合方法无关。为了看到这一点，我们假设存在一个函数f，该函数给出特定的最佳位置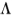。也就是说，我们找到f 使得

现在假设我们寻求第二个函数f_w，该函数给出最佳的定位效果，而其信噪比固定为不同的值，即

 如果现在根据f_w(x)定义f₁(x)为f_w(x)= f_w(xw) 其中

 

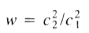
然后将（24）中对f_w 的约束转换为对f₁ 的约束，该约束与（23）相同，并且（24）可以重写为

其解为f₁ = f。因此，如果我们找到一个这样的函数f，则可以通过缩放f 获得任何固定信噪比的最大定位。台阶边缘检测的设计问题具有一个唯一的解决方案（最大为空间缩放），而与信噪比或定位的绝对值无关。

最优滤波器由（22）隐式定义，但是在应用变化演算之前，我们必须稍稍变换问题。具体来说，我们将（22）的最大化转化为仅涉及积分函数的约束最小化。 （22）中除一个积分外的所有积分均设置为不确定的常数。然后，我们根据未确定的常数找到剩余积分的极值（因为它将与总表达式中的极值相对应）。然后选择常量的值，以使原始表达式最大化，该表达式现在仅是这些常量的函数。给定常数，我们可以唯一地指定函数f（x），该函数给出最大的复合准则。

第二种修改涉及积分的极限。分母（22）的两个积分的极限为 + W和 -W，而分子的积分的极限为0，另一个为 -W。由于函数f 应该是反对称的，我们可以使用后者的极限对于所有积分。分母积分在该子范围内的值将是它们在整个范围内的值的一半。而且，这使得能够将f'（0）的值设置为边界条件，而不是表示为f“的积分。如果要最小化的积分与约束积分具有相同的限制，则可以利用等参约束条件（参见[6，p.216]）。当满足此条件时，可以使用约束函数的拉格朗日乘子将约束优化简化为无约束优化，找到（22）的最大值的问题简化为SNR的分母中的积分最小化，但要受其他积分保持恒定的约束，根据对等原理，我们可以选择在保持其他积分不变的情况下对任何一个积分进行极值化，因此解应为相同。

我们从允许函数的空间中寻找一些函数f，该函数应使积分最小化

服从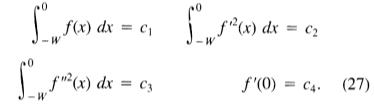

在这种情况下，允许函数的空间将是满足某些边界条件（即 f（0）= 0 和 f（-W）= 0）的所有连续函数的空间。这些边界条件对于确保对积分进行求值是必要的在有限的极限上，精确地表示了无限的卷积积分。也就是说，如果f的n阶导数出现在某个整数中，则该函数的（n-1）一阶导数必须在（-oo，+ oo）范围内连续。这意味着f及其一阶导数（n-1）的值在积分极限时必须为零，因为它们在此范围之外为零。

要最小化的函数的形式为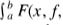f'，f“)，我们可以用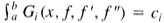的形式写出一系列约束。由于约束是等距的，即它们与最小化积分具有相同的积分极限，因此我们可以使用拉格朗日乘数[6]形成复合函数。泛函是出现在要最小化的表达式中和约束中的泛函的线性组合。找到的无约束极大化的解决方案等同于找到约束问题的解决方案。复合函数是

 

代，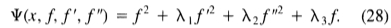

从该方程的形式可以看出，对哪个积分进行了极值化和哪些约束是任意的选择，其解将是相同的。这是前面提到的互惠的一个例子。从分母中选择积分很方便，因为标准形式的变分问题是最小化问题。对应于函数的欧拉方程为


其中_f 表示相对于f 的的偏导数，等等。我们用Euler方程中的（28）代替，得出：

该微分方程的解是一个常数和一组e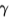^x形式的四个指数的总和，其中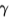从相应的齐次微分方程的解中得出。现在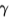必须满足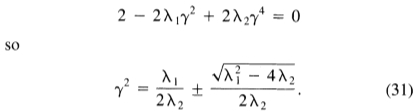


根据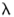1和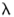2的值，该方程式的根可能纯粹是虚数，纯粹是实数或复杂。从复合函数中，我们可以推断出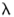2为正（因为f“ ²的积分要最小化），但不清楚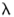1的正负号或大小应该是什么。欧拉方程为存在提供了必要条件通过建立这样的条件，我们可以解决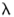1值的歧义，为此，我们必须考虑函数的第二种变化形式。让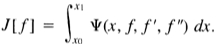

然后根据泰勒定理（另请参见[6，p.214]），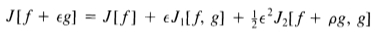

其中p是介于0和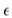之间的某个数字，而g是从允许函数的空间中选择的，其中

请注意，J₁等于g乘以f 的欧拉方程的积分（使用部分积分进行转换），并且如果f 满足欧拉方程，则J₁将为零。 现在我们可以将第二个变化定义为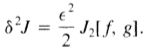

最小值的必要条件是>0。我们从（28）计算的第二阶偏导数，得到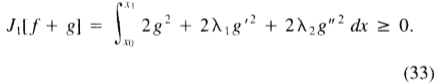

利用g是一个允许函数并因此在积分极限处消失的事实，我们通过集成将以上部分转换为

可以写成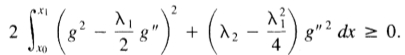

如果对所有x积分的表达式均为正，则保证积分为正，因此，如果

 

那么对于所有x和任意g，积分将为正，并且极值将为最小值。如果我们回到（31），我们发现这个条件恰好是给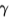赋复数根的条件，因此我们既保证了最小值的存在，又以解决方案的形式解决了可能的歧义。现在，我们可以进行推导，并假设形式为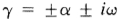且oa为w real的四个复数根。现在X并将实部和虚部等于（31），我们得到

现在，我们可以进行推导，并假设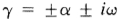的四个复数根为，w real。现在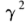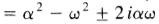并将实部和虚部等于（31），我们得到

现在可以写出[-W，0]范围内的一般解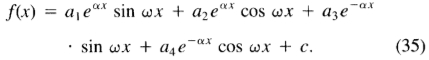

此功能受边界条件的限制

其中s是一个未知常数，等于该函数在原点处的斜率。由于f（x）是非对称的，因此可以使用f（-x）= -f（x）将上述定义扩展到[-W，W]范围。四个边界条件使我们能够根据未知常数，w，c和s求解量a1至a4。边界条件可能会被重写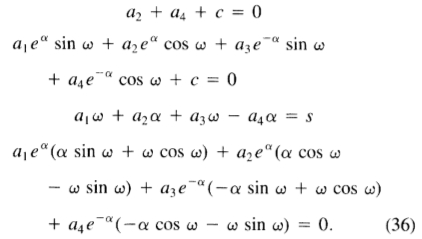

这些方程在四个未知数a1，a2，a3，a4中是线性的，求解后得出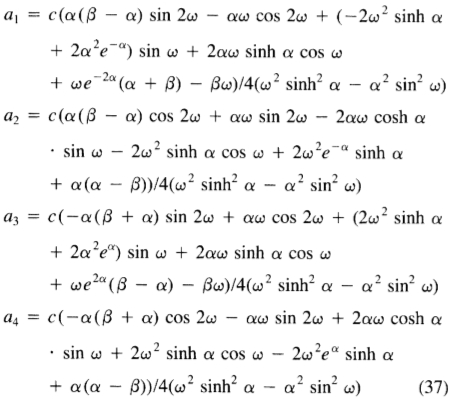

其中是原点处的斜率s除以常数c。通过检查这些表达式，我们可以看到通过将替换为 -可以从a1获得a3，并且类似地对于a2可以获取a4。

现在，函数已根据常数，w，和c 进行了参数化。我们仍需找到这些参数的值，这些参数可使构成我们的复合准则的积分的商数最大化。为此，我们首先用项表示每个积分由于这些积分非常长且无趣，因此此处未给出，但可以在[4]中找到，我们已经将函数的无穷维空间上的优化问题简化为三个变量a的非线性优化，w和（不足为奇，组合准则不依赖于c）。不幸的是，所得准则仍然必须满足多重响应约束，可能太复杂而无法解析求解，必须使用数值方法来提供最终的解决方案。

形状的变化将取决于多重响应约束，即它将取决于我们迫使相邻响应的距离。图5显示了由该距离的特定选择得出的操作符。回想一下，对于任意w 没有唯一的最佳函数，而是一类通过用w 缩放原型函数获得的函数。随着图像中信噪比的降低，我们将希望进一步将响应分开，但是尚不清楚单个操作员的信噪比值是多少。在使用该运算符的情况下，可以使用几个运算符宽度，并应用决策程序来选择输出信噪比高于固定阈值的最小运算符。通过这种安排，操作员将花费大部分时间接近其输出 阈值进行操作。我们尝试选择一个间距，对于该间距，多重响应错误的概率与阈值导致的错误概率可比。

可以如下形成对真实最大值附近的虚假最大值的概率的粗略估计。如果我们看一个理想步骤的响应，我们发现它的二阶导数在x = 0 处具有幅度 |Af'（0）|。如果 |Af'（0）| 大于边沿，则在边缘中心附近将只有一个最大值。仅对噪声的响应的二阶导数。后者的数量表示为s_n是具有标准偏差的高斯随机变量

 

噪声斜率s_n超过 Af'（0）的概率p_m由正态分布函数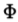给出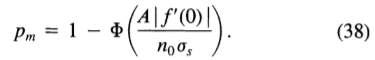

我们可以为此概率选择一个值作为可接受的错误率，这将确定 f'（0）与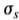的比率。我们可以将多重响应p_m的概率与错误标记边缘p_f 的概率相关联，即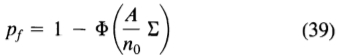

通过设置p_m = p_f。这是很自然的选择，因为它使检测错误或多重响应错误的可能性均等。然后从（38）和（39）

实际上，不可能找到满足此约束的过滤器，因此我们搜索满足以下条件的过滤器

其中r尽可能接近1。图4给出了几个滤波器的性能指标和参数值。通过将c固定为c = 1，可以从（37）中找到所有这些滤波器的a_i系数。 不幸的是，对于表中的6号滤波器，使用约束数值优化可以获取的r 的最大值约为0.576。在我们的实现中，我们已使用高斯的一阶导数来对该滤波器进行了逼近，如下一节所述。

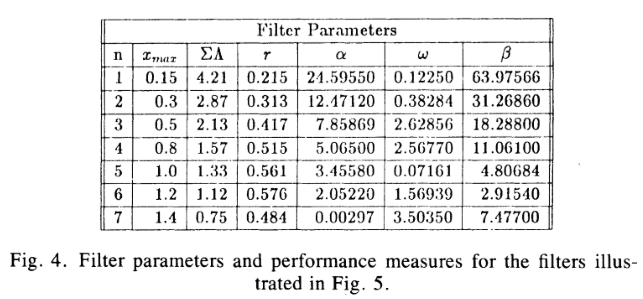
图4：图5所示的过滤器的过滤器参数和性能指标。

高斯算子的一​​阶导数，甚至滤波器6本身，即使就我们使用的标准而言，也不应视为边缘检测滤波器中的最终词。如果我们愿意忍受多重响应性能r的轻微降低，则可以在其他两个标准上获得显着改善。例如，过滤器4和5都比过滤器6具有更好的EA乘积，而r 却略低。从图5中我们可以看到，这些滤波器在原点处具有较陡的斜率，这表明性能增益主要集中在本地化，尽管尚未通过实验进行验证。这些其他算子还需要进行彻底的经验比较，这种情况下的理论尚不清楚如何最佳地进行权衡。

V 有效逼近

在最后一部分中得出的作为滤波器编号6的运算符，如图6所示，可以通过高斯G'（x）的一阶导数来近似，其中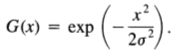

这样做的原因是，如果可以将滤波器表示为高斯的某种导数，则有非常有效的方法来计算滤波器的二维扩展。这在其他地方[4]中有详细描述，但是目前，我们将高斯滤波器的一阶导数的理论性能与最优算子进行比较。一阶导数滤波器的脉冲响应为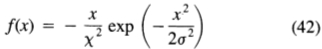

绩效标准中的条款具有值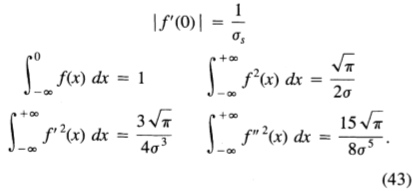

该运营商的整体绩效指数是

 

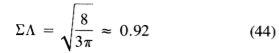
而r值来自（41），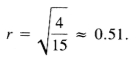

上面的高斯算子的一​​阶导数的性能比最优算子差约20％，其多重响应度量r 则差约10％。通过查看两个算子在真实图像上的性能可能很难检测到这种程度的差异，并且由于可以在二维上以更少的精力来计算高斯算子的一​​阶导数，因此仅将其用于实验。可以将两个算子的脉冲响应进行比较，如图6所示。

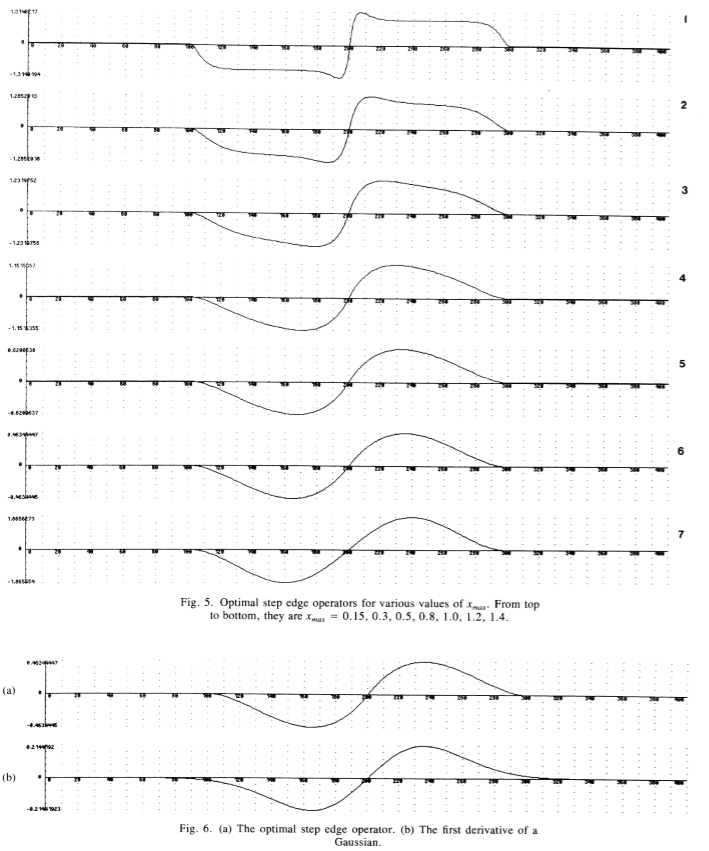
图5：各种x值的最佳阶梯边缘算子，从上到下分别为x = 0.15、0.3、0.5、0.8、1.0、1.2、1.4。
图6：（a）最佳阶梯边缘算子。 （b）高斯的一阶导数。

Macleod [16]提出了高斯算子的一​​阶导数的近似值，用于步沿检测。 Macleod的算子是两个位移的二维高斯的差。在Fram和Deutsch [7]中对其进行了评估，并与该论文中考虑的其他几种方案进行了比较。 Marr和Hildreth [18]建议与高斯算子的拉普拉斯算子也有很强的联系。实际上，一维Marr-Hildreth边缘检测器与我们得出的算子几乎相同，因为一阶导数算子的输出最大值将对应于Marr和Hildreth使用的Laplacian算子的零交叉。但是，在两个维度上，与拉普拉斯算子相比，我们的检测器的方向性增强了其检测和定位性能。另一个重要的区别是，最大响应幅度可以很好地估计边缘强度，因为SNR标准是该响应与噪声响应的比率。 Marr-Hildreth运算符不使用任何形式的阈值处理，但是可以使用自适应阈值处理方案来利用我们的一阶导数运算符。在下一部分中，我们将介绍这样一种方案，其中包括噪声估计和一种用于沿轮廓线对边缘点进行阈值处理的新颖方法。

 我们推导了最优算子来处理高斯噪声中已知的图像特征。纹理区域之间的边缘检测是另一个重要问题。如果可以将纹理建模为某些滤波器t（x）对高斯噪声的响应，则这很简单。然后我们可以将纹理视为噪声信号，并且滤波器f（x）对纹理的响应与滤波器（f * t）（x）对高斯噪声的响应相同。在计算噪声响应的性能标准的每个积分中进行此替换会给我们带来纹理边缘设计问题。将其推广到其他类型的纹理并不是那么容易，并且为了在已知纹理类型之间进行良好的区分，一种更好的方法将涉及[5]中的马尔可夫图像模型。

VI 噪声估计和阈值

为了估计来自操作员输出的噪声，我们需要能够将其对噪声的响应与阶跃边缘引起的响应分开。由于系统的性能将严重取决于此估计的准确性，因此也应将其表述为优化。维纳滤波是一种最佳估计两分量信号中一个分量的方法，可以在本应用中发挥优势。它需要了解两个组件的自相关函数以及组合信号。一旦噪声成分被最佳分离，我们就形成了噪声幅度的整体直方图，并从噪声信号的某个固定百分位数估算出噪声强度。

令g₁(x)是我们要检测的信号（在这种情况下为噪声输出），而g₂(x)是一些干扰（反常地，这将是我们滤波器的边缘响应），然后表示g的自相关函数，g为R₁₁(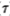)，g₂为R₂₂(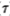)，互相关为R₁₂(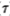)，其中两个实函数的相关性定义如下：

在这种情况下，我们假定信号和干扰是不相关的，因此R₁₂(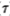)=0。最佳滤波器是K（x），其隐式定义如下[30]：

由于响应白噪声的滤波器输出的自相关等于其冲激响应的自相关，我们有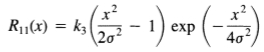

如果g₂是在（42）中推导的运算符对阶跃边缘的响应，则我们将得到g₂(x)= k exp(-x/2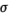²)和

 

在边缘的幅度大于噪声的情况下，R₂₂ + R₁₁近似为高斯，而R₁₁是相同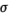的高斯的二阶导数。那么，K的最佳形式是脉冲函数的二阶导数。

上面的滤波器K 与边缘检测算子的输出进行卷积，结果取平方。下一步是从局部值估计均方噪声。这里有几种可能性。最简单的方法是使用移动平均滤波器或通过对整个图像取平均值来对某个邻域的平方值求平均。不幸的是，经验表明，滤波器K 对阶跃边缘非常敏感，结果，任何形式的平均噪声估计都因边缘的密度和强度而严重着色。

为了更好地分离信号和噪声，我们可以利用以下事实：对于边缘和噪声，滤波器响应的幅度分布趋于不同。根据我们的模型，噪声响应应具有高斯分布，而阶跃边缘响应将由不经常出现的大值组成。如果我们对滤波器值进行直方图处理，我们应该发现低百分位（例如小于80％）的位置将主要由噪声能量确定，因此它们是有用的噪声估计器。该算法的当前实现中实际使用了全局直方图估计。

即使采用噪声估计，如果边缘检测器仅使用单个阈值，也将容易出现条纹。条纹是由于操作员的输出沿着轮廓的长度在阈值之上和之下波动而导致的边缘轮廓破裂。假设我们在T₁ 处设置了一个阈值，并且图像中存在一条边缘，使得操作员的响应的平均值为T₁。即使噪声很小，由于噪声，输出幅度也会有一些波动。我们期望轮廓仅在阈值的一半左右才高于阈值。这导致边缘轮廓断裂。尽管这是一种病理情况，但是对于采用阈值处理的边缘检测器，条纹是一个非常普遍的问题。设置阈值非常困难，因此在保留高灵敏度的同时标记噪声边缘的可能性很小。条纹效果的示例在图7中给出。

 

图7：（a）576 x 454像素的零件图像。 （b）在T₁保留的图像。 （c）图像阈值为2 T₁。 （d）使用（a）和（b）中的阈值对图像进行滞后阈值处理。

Pentland [22]使用具有Marr-Hildreth零交叉点的方法来解决这个问题，一种可能的方法是在轮廓的一部分长度上平均轮廓的边缘强度。如果平均值高于阈值，则标记整个段。如果平均值低于阈值，则轮廓中不会出现任何部分。通过以最大曲率断开轮廓来分割轮廓。在零交叉的情况下，这种分割是必要的，因为零交叉始终形成闭合的轮廓，而轮廓显然并不总是与图像中的轮廓相对应。

在当前算法中，没有尝试对轮廓进行预分割。取而代之的是通过滞后进行阈值处理。如果轮廓的任何部分高于高阈值，则这些点将立即输出，轮廓的整个连接段也将被输出，该轮廓段包含这些点并且位于低阈值之上。条纹的可能性大大降低，因为要使轮廓破裂，它现在必须在高阈值以上和低阈值以下波动。而且，由于这些点的强度必须高于较高阈值，因此降低了孤立的虚假边缘点的可能性。实现中的高阈值与低阈值之比在二或三对一的范围内。

Ⅶ 二维或更多维

在一个维度上，我们可以使用一个位置坐标来表征空间中台阶边缘的位置。在二维中，边缘也具有方向。在本节中，我们将使用术语“边缘方向”来表示与边缘在二维中定义的轮廓相切的方向。假设我们希望检测特定方向的边缘。我们通过将垂直于边缘方向对齐的线性边缘检测函数与平行于边缘方向的投影函数进行卷积来为此方向创建二维蒙版。如果投影函数是与用作检测函数的高斯（一阶高斯）相同的高斯，则可以节省大量的计算工作量。通过用对称的二维高斯卷积图像，然后垂直于边缘方向进行微分，可以创建此类蒙版。实际上，我们不必在每个方向上都执行此操作，因为可以从光滑表面在两个方向上的坡度精确地确定光滑表面在任何方向上的坡度。这种形式的定向算子虽然计算简单且成本低廉，但却构成了更为复杂的检测器的核心，这将在接下来的几节中进行介绍。

 

假设我们希望使用算子G_n对图像进行卷积，算子G_n是二维高斯G在某个方向n上的一阶导数，即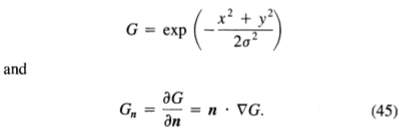

理想情况下，n应该垂直于要检测的边缘的方向定向，并且尽管该方向不是先验的，但我们可以从平滑的梯度方向对其进行很好的估计

其中*表示卷积。事实证明，这是对步长的边缘法线方向的很好估计，因为平滑的步长具有垂直于边缘的强梯度。在没有噪声的情况下，它非常适合直线边缘，并且高斯平滑使它对噪声相对不敏感。

 

边缘点定义为应用于图像I的算子Gn的局部最大值（沿n方向）。在局部最大值处，我们有

并用（45）代替G_n并关联高斯卷积

在这样的边缘点，边缘强度将是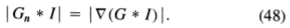

由于卷积的关联性，我们可以先与对称高斯G卷积，然后计算方向二阶导数零以定位边缘（47），然后使用（48）的大小估算边缘强度。这等效于使用方向算子G_n检测和定位边缘，但是在卷积之前我们不需要知道方向n。

Torre和Poggio [28]和Haralick [10]也使用了（47）中非线性二阶导数算子的形式。在边缘增强的背景下，它也出现在Prewitt [23]中。 Spacek [26]提出了一种截然不同的二维扩展，他使用垂直于边缘方向排列的一维滤镜，但未沿边缘方向扩展它们。 Spacek从一维公式开始，该公式最大化了第二节中定义的三个性能标准的乘积，并导致了阶跃边缘算子，该算子与我们在第四节中得出的算符略有不同。 Gennert [8]直接解决了二维边缘检测器问题，并在图像的每个点上应用了一组定向一阶导数算子。操作员沿边缘方向的范围有限，并且在边缘方向和拐角急剧变化时会产生良好的效果。

运算符（47）实际上通过在边缘方向上的二阶导数中定位零交叉来定位最大值或最小值。原则上，通过首先将图像与对称的n维高斯卷积，可以将其用于任意尺寸的边缘检测器。由于高斯可分为n个一维滤波器，因此使用n维高斯卷积非常高效。

但是，使用平滑投影函数（例如高斯函数）还有其他更为紧迫的原因。当我们将线性算子应用于二维图像时，我们在输出的每个点上形成一些输入值的加权和。对于此处描述的边缘检测器，该总和将是边缘不同侧的局部平均值之间的差。在非最大抑制之前，此输出表示图像的一种移动平均值。理想情况下，我们希望使用无限的投影函数，但实际边缘的范围有限。因此，有必要使投影功能[9]窗口化。如果窗口功能突然被截断，例如，如果它是矩形的，则由于该窗口的带宽很高，因此滤波后的图像将不平滑。这种影响与傅立叶理论中的吉布斯现象有关，该现象在有限的窗口上转换信号时发生。当对这个粗略信号应用非最大抑制时，我们发现边缘轮廓倾向于“漂移”，或者在严重的情况下甚至不连续。

解决方案是使用平滑窗口功能。在统计中，汉明窗和汉宁窗通常用于移动平均值。高斯是这两者的合理近似值，对于给定的空间宽度，它当然具有非常低的带宽。 （高斯函数是唯一的函数，带宽和频率的乘积极小。）对于较大的操作员规模，窗口函数的影响变得非常明显，这可能是只有在Marr和希尔德雷斯在拉普拉斯
高斯。

 

在这里有必要将这种有向二阶导数算子的性能与拉普拉斯算子进行比较。首先我们注意到，二维拉普拉斯算子可以在两个任意正交方向上分解为二阶导数的分量。如果我们选择在主梯度方向上采用导数之一。我们发现运算符输出将包含一个与上述运算符基本相同的贡献，以及一个沿边缘方向对齐的贡献。第二个成分对定位或检测没有任何作用（表面在该方向上大致恒定），但会增加输出噪声。

在后面的部分中，我们将描述一种边缘检测器，该检测器结合了不同方向和纵横比的算子，但是它们是上述简单检测器中所用算子的超集。在典型图像中，大多数边缘由宽度最小的算符标记，而大多数则由无长度的算符标记。在这些情况下，简单的检测器表现良好，并且随着检测器复杂度的增加，性能增益趋于降低。但是，正如我们将在以下各节中看到的那样，在某些情况下应使用更大或更多个定向运算符，并且在适用时它们确实会提高性能。使这种复杂的探测器产生相干输出的关键是设计有效的决策程序，以便在图像中每个点的操作员输出之间进行选择。


Ⅷ 多重宽度的需求

在确定了操作员的最佳形状之后，我们现在面临选择操作员宽度的问题，以便在特定应用中提供最佳的检测/定位权衡。通常，图像中每个边缘的信噪比都将不同，因此有必要在方案中合并多个宽度的运算符。必须由算法动态决定使用哪个运算符，这需要对候选边缘周围区域中的噪声能量进行局部估计。一旦知道了噪声能量，就将知道每个运算符的信噪比。如果然后使用噪声的概率分布模型，则可以有效地计算候选边缘为假边缘的概率（对于给定的边缘，此概率对于不同的运算符宽度将有所不同）。

如果我们假设与错误检测的边缘相关的先验惩罚与边缘强度无关，则应根据错误的概率而非响应的大小对检测器的输出进行阈值化。一旦设置了概率阈值，就可以确定最小可接受的信噪比。但是，可能会有几个运算符的信噪比高于阈值，在这种情况下，应选择最小的运算符，因为它可以提供最佳的定位。我们可以对阈值的设置保持保守，因为最小的运算符错过的边缘可能会被较大的运算符拾取。有效的全球tradeoffbetween错误率和定位保持，因为选择高信噪比阈值导致较低的错误率，但往往会得到较差的定位，因为较少的边缘将会从较小的运营商被记录。

总而言之，在操作员输出之间进行选择的第一种启发式方法是，每当操作员具有足够的E时，都应使用较小的操作员宽度。这类似于Marr和Hildreth [18]提出的在高斯通道的不同拉普拉斯算子之间进行选择的选择标准。在他们的情况下，该论据是基于以下观察：较小的信道具有较高的分辨率，即，来自相邻边缘的干扰的可能性较小。该论点在当前情况下也非常重要，因为迄今为止，尚未考虑给定的操作员支持中有多个优势的可能性。有趣的是，Rosenfeld和Thurston [25]在选择纹理边缘检测算子时提出了完全相反的标准。给出的论据是，较大的算子可以提供更好的平均，因此（大概）可以提供更好的信噪比。

 

以精细到粗略的启发式为起点，我们需要形成一个本地决策程序，当邻居中的多个操作员做出响应时，该决策程序将使我们能够决定是否标记一个或多个边缘。如果宽度最小的操作员对边缘做出响应，并且其信噪比高于阈值，则应立即在该点标记边缘。现在我们面临的问题是，几乎肯定会有较大的运算符标记的边，但是这些边可能不会与第一个边恰好重合。对此的可能答案是抑制所有附近操作员的输出。这具有防止大通道响应叠加在尖锐边缘上的“模糊”边缘的不良效果。

相反，我们使用“功能综合”方法。我们首先标记最小的算子的所有边。从这些边缘，我们合成了大型运算符输出，而如果这些是图像中仅有的边缘，则将产生较大的运算符输出。然后，我们将实际的运算符输出与综合输出进行比较。仅当大型操作员的响应比我们从合成输出中预测的响应大得多时，才标记其他边。产生合成输出的最简单方法是在特定方向上获取由小算符标记的边缘，并对该算符以与边缘方向垂直的高斯进行卷积。高斯的a应与大通道检测滤波器的a相同。

可以重复应用此过程，以首先标记第二个最小比例尺上没有被第一个标记的边缘，然后从第三个比例尺上找到前两个都没有标记的边缘，等等。因此，我们构建了通过在每个比例尺上未用较小比例尺标记的那些边上添加一个累积边线图。事实证明，在许多情况下，大多数边缘是由最小的通道拾取的，而后面的通道则主要标记阴影和阴影边缘或纹理区域之间的边缘。

 

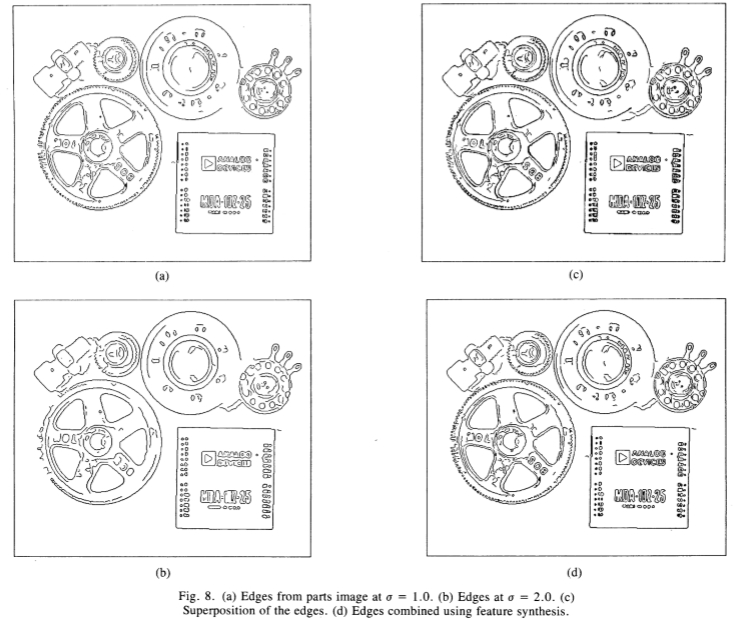
图8：（a）零件图像在a = 1.0时的边缘。 （b）a = 2.0时的边。 （c）边缘重叠。 （d）使用特征综合来合并边缘。

图9：（a）Handywipe图像576 x 454像素。 （b）a = 1.0时，手擦图像的边缘。 （c）＝ 5.0。 （d）边缘重叠。 （e）使用特征综合来合并边缘。

在图1和图2中示出了应用于一些样本图像的特征合成的一些示例。参见图8和9。请注意，图8中的大多数边缘由较小的比例运算符标记，而较粗的比例仅拾取了一些其他的边缘，主要是阴影。但是，当两组边缘重叠时，我们注意到在许多情况下，两个算子对同一边缘的响应在空间上并不重合。当应用特征综合时，我们发现消除了较大算子的冗余响应，从而生成了清晰的边缘图。

相反，在图9中，由两个算子标记的边缘基本上是独立的，并且边缘的直接叠加给出了有用的边缘图。当我们将特征合成应用于这些边缘集时，我们发现保留了较粗比例的大部分边缘。两个无花果。由边缘检测器产生的参数8和9具有完全相同的一组参数（而不是运算符大小），并且选择它们来表示跨比例的图像内容的相反极端。

IX 方向运营商的需求

到目前为止，我们已经假定投影函数是高斯函数，并且与用于检测函数的高斯函数相同。实际上，随着投影功能的长度增加，操作员的检测和定位都得到改善。现在，我们针对操作员的信噪比证明这一点。本地化的证明是相似的。我们将考虑在x方向上穿过原点的阶梯边缘。该边缘可用等式表示

其中u_-1是单位步长函数，而A是边缘的振幅，如前所述。假设存在每单位面积均方值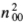的加性高斯噪声。如果我们将该信号与滤波器的卷积响应进行卷积处理，则滤波器的固有响应为f（x，y），则对边缘的响应（在原点处）为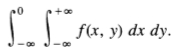


仅对噪声的均方根响应为

信噪比是这两个积分的商，将由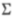表示。我们已经看到，如果将标准函数缩放到边缘，会发生什么（21）。现在，通过将f（x，y）替换为f₁(x,y)= f(x,(y|l ))，对投影函数执行相同的操作。积分变成

 

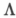两者的比例现在为。本地化也提高了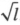。显然希望我们使用尽可能大的投影函数。然而，对此存在实际限制，特别是图像中的边缘范围有限，并且很少有完全线性的。但是，大多数边缘会持续一段距离，实际上比大多数边缘算子的3或4像素支撑要远得多。即使是弯曲的边缘，也可以通过足够小的比例的线性段来近似。考虑到优点，显然最好在适用时使用定向运算符。唯一的条件是检测方案必须确保仅在图像适合线性边缘模型时才使用它们。

本算法通过形成拟合优度估计来测试每个方向性掩模的适用性。它在计算遮罩本身的同时执行此操作。形成长方向性遮罩的有效方法是对具有相同方向的非延长遮罩的输出进行采样。该输出在平行于边缘方向的直线中以固定间隔采样。如果样品靠得很近（相距小于2），则所得的遮罩在其沿边缘方向的大部分范围内基本上是平坦的，并且在其端部会平滑地降至零。在图10中示出了这种面罩的两个横截面。在该图中（与本实施方式一样），在操作者支架上有五个样品。

 

图10：方向台阶边缘罩。 （a）平行于边缘方向的横截面。 （b）垂直于边缘方向的横截面。 （c）几个掩模的二维脉冲响应。

在计算蒙版的同时，可以通过简单的平方误差度量来确定拟合优度。通过将一行中的一定数量的圆形蒙版输出（例如5）相加来计算蒙版。如果蒙版在其首选方向上位于台阶边缘上，则这5个值将大致相同。如果边缘是弯曲的或与蒙版方向不对齐，则值将变化。我们使用这些值的方差作为实际边缘与理想阶跃模型拟合优度的估计。然后，如果方差的方差大于平方输出的一部分，则我们将其抑制。如果没有方向算子在一点上具有足够的拟合优度，则该算法将使用第VII节中所述的非延长算子的输出。这种简单的拟合优度度量足以消除传统上困扰定向操作员的问题，例如对高度弯曲的边缘的错误响应以及边缘超出拐角的扩展；参见希尔德雷斯[12]。

投影函数的这种特殊形式，即在某个范围内具有恒定值的函数，该函数在两端大约用两个半高斯衰减到零，这与汉宁窗的常用扩展非常相似。后一个函数在一段距离上是平坦的，并在两端用两个半余弦钟形衰减至零[2]。因此，我们可以期望我们的函数作为移动平均估计器具有良好的属性，正如我们在第七节中所看到的那样，这是投影函数所扮演的重要角色。

定向算子的设计中要做的所有工作就是确定方向数，或者等效地，确定两个相邻方向之间的夹角。为了确定后者，我们需要确定方向性操作员的角度选择性，该角度选择性是边缘方向和操作员首选方向之间的角度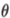的函数。假设我们通过取2N +1个奇数样本构成算子。设样本数为n，其中n在-N ... + N范围内。回想一下，方向算子是通过与对称高斯卷积形成的，将其垂直于算子的首选边缘方向微分，然后沿首选方向采样。区别表面将是与优选边缘方向成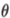°角的脊。它的高度将随着cos 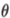的变化而变化，第n个样本到脊中心的距离将为nd sin 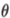，其中d是样本之间的距离。归一化的输出将是


如果存在m个操作员方向，则两个相邻操作员的首选方向之间的角度将为180 / m。因此，边缘与最近的首选操作员方向之间的最坏情况角度为90 / m。在当前实施中，d/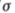的值约为1.4，并且有6个操作员方向。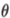的最坏情况是15度，在这种情况下，操作员的输出将下降到最大值的85％左右。方向算子很像我们所推导的算子，是由Marr [17]提出的，但被高斯的拉普拉斯算子抛弃了[18]。部分原因是因为认为图像中每个点的多个定向算符的计算需要大量的计算。实际上，上述采样方案每个运算符仅需要五个乘法。使用五点方向算子进行边缘检测的示例在图11中给出。

 

图11：（a）Dalek图像576 x 454像素。 （b）使用圆形算子找到的边。 （c）方向边缘（6个遮罩方向）。

 

Ⅹ 结论

我们已经描述了用于任意边缘轮廓的边缘检测器的设计过程。该设计基于数学形式的检测和定位标准的规范。为了充分捕捉良好检测的直觉，有必要用多重响应度量来扩充原始的两个标准。提出了标准的数学形式，并使用数值优化来找到屋顶和山脊边缘的最佳算子。然后，分析仅限于考虑阶梯边缘的最佳算子。结果是一类与空间比例相关的算子。在检测性能与本地化之间存在直接的权衡，这取决于空间宽度。最佳阶跃边缘算子的脉冲响应显示为近似高斯的一阶导数。

提出了一种检测器，该检测器使用带有滞后的自适应阈值消除边缘轮廓的条纹。根据由噪声估计方案确定的图像中的噪声量来设置阈值。该检测器利用几种操作员宽度来应对变化的图像信噪比，并使用一种称为特征合成的方法将操作员输出进行组合，其中较小操作员的响应可用来预测较大操作员的响应。如果实际的大型操作员输出与预测值明显不同，则会标记新的边缘点。因此，有可能描述以不同比例出现的边缘，即使它们在空间上是重合的。

在二维中，表明在梯度方向上以梯度幅度的最大值标记边缘点等同于找到某个非线性微分算子的零交叉。结果表明，当边缘轮廓局部为直线时，与圆形支撑的操作器相比，高方向性的操作器将提供更好的结果。提出了一种在多个方向上高效生成高方向性蒙版并将其集成到单个描述中的方法。在这项工作的可能扩展中，最有趣的未解决问题是将不同的边缘检测器输出集成到单个描述中。实施了一种使用特征综合来结合边缘和脊检测器输出的方案，但结果尚不确定。与没有规模的边缘算子相比，这里的问题要复杂得多，因为没有明显的理由偏爱一个边缘类型。每个边缘集必须彼此合成，而不能因一个方向上的高估而产生偏差。

我们提出的标准可以稍作修改即可用于其他类型的操作员的设计。例如，我们可能希望设计用于非线性二维特征（例如拐角）的检测器。在这种情况下，检测标准将是类似于（3）的二维积分，而合理的定位标准将需要考虑边缘位置在x和y方向上的变化，并且不会直接根据（9）。对高维边缘的检测具有自然的概括，例如在断层扫描中出现在材料边界处。如第VII节所指出的，（47）可用于查找任意维图像中的边缘，并且该算法在较高维中仍然有效，因为n维高斯卷积可以分解为n个线性卷积。

致谢
作者要感谢J. M. Brady博士对这项工作的影响以及对本文早期草案的评论。感谢裁判们的建议，这些建议极大地改善了论文的表达方式。特别要感谢裁判员提出的基于p上Schwarz不等式的简单推导。 682。

 

 

参考文献

[1] R. J. Beattie, "Edge detection for semantically based early visual processing," Ph.D. dissertation, Univ. Edinburgh, 1984.
[2] C. Bingham, M. D. Godfrey, and J. W. Tukey, "Modem techniques of power spectrum estimation," IEEE Trans. Audio Electroacoust., vol. AU-15, no. 2, pp. 56-66, 1967.
[3] R. A. Brooks, "Symbolic reasoning among 3-D models and 2-D images," Dep. Comput. Sci., Stanford Univ., Stanford, CA, Rep. AIM343, 1981.
[4] J. F. Canny, "Finding edges and lines in images," M.I.T. Artificial Intell. Lab., Cambridge, MA, Rep. Al-TR-720, 1983.
[5] F. S. Cohen, D. B. Cooper, J. F. Silverman, and E. B. Hinkle, "Simple parallel hierarchical and relaxation algorithms for segmenting textured images based on noncasual Markovian random field models," in Proc. 7th Int. Conf. Pattern Recognition and Image Processing, Canada, 1984.
[6] R. Courant and D. Hilbert, Methods of Mathematical Physics, vol. 1. New York: Wiley-Interscience, 1953.
[7] J. R. Fram and E. S. Deutsch, "On the quantitative evaluation of edge detection schemes and their comparison with human performance," IEEE Trans. Comput., vol. C-24, no. 6, pp. 616-628, 1975.
[8] M. Gennert, "Detecting half-edges and vertices in images," in IEEE Conf. Comput. Vision and Pattern Recognition, Miami Beach, FL, June 24-26, 1986.
[9] R. W. Hamming, Digital Filters. Englewood Cliffs, NJ: PrenticeHall, 1983.
[10] R. M. Haralick, "Zero-crossings of second directional derivative edge operator," in SPIE Proc. Robot Vision, Arlington, VA, 1982.
[11] A. Herskovits and T. O. Binford, "On boundary detection," M.I.T. Artificial Intell. Lab., Cambridge, MA, Al Memo 183, 1970.
[12] E. C. Hildreth, "Implementation of a theory of edge detection," M.I.T. Artificial Intell. Lab., Cambridge, MA, Rep. AI-TR-579, 1980.
[13] -, The Measurement of Visual Motion. Cambridge, MA: M. I.T. Press, 1983.
[14] B. K. P. Horn, "The Binford-Horn line-finder," M.I.T. Artificial Intell. Lab., Cambridge, MA, Al Memo 285, 1971.
[15] D. G. Luenberger, Introduction to Linear and Non-Linear Programming. Reading, MA: Addison-Wesley, 1973.
[16] I. D. G. Macleod, "On finding structure in pictures," in Picture Language Machines, S. Kaneff, Ed. New York: Academic, 1970, p. 231.
[17] D. C. Marr, "Early processing of visual information," Phil. Trans. Roy. Soc. London, vol. B 275, pp. 483-524, 1976.
[18] D. C. Marr and E. Hildreth, "Theory ofedge detection," Proc. Roy. Soc. London., vol. B 207, pp. 187-217, 1980.
[19] D. C. Marr and T. Poggio, "A theory ofhuman stereo vision," Proc. Roy. Soc. London., vol. B 204, pp. 301-328, 1979.
[20] J. E. W. Mayhew and J. P. Frisby, "Psychophy.sical and computational studies toward a theory of human stereopsis," Artificial Intell. (Special Issue on Computer Vision), vol. 17, 1981.
[21] T. Poggio, H. Voorhees, and A. Yuille, "A regularized solution to edge detection," M.I.T. Artificial Intell. Lab., Cambridge, MA, Rep. AIM-833, 1985.
[22] A. P. Pentland, "Visual inference of shape: Computation from local features," Ph.D. dissertation, Dep. Psychol., Massachusetts Inst. Technol., Cambridge, MA, 1982.
[23] J. M. S. Prewitt, "Object enhancement and extraction," in Picture Processing and Psychopictorics, B. Lipkin and A. Rosenfeld, Eds. New York: Academic, 1970, pp. 75-149.
[24] S. 0. Rice, "Mathematical analysis of random Noise," Bell Syst. Tech. J., vol. 24, pp. 46-156, 1945.
[25] A. Rosenfeld and M. Thurston, "Edge and curve detection for visual scene analysis," IEEE Trans. Comput., vol. C-20, no. 5, pp. 562569, 1971.
[26] L. Spacek, "The computation of visual motion," Ph.D. dissertation, Univ. Essex at Colchester, 1984.
[27] K. A. Stevens, "Surface perception from local analysis oftexture and contour," M.I.T. Artificial Intell. Lab.,Cambridge,MA,Rep.AlTR-512, 1980.
[28] V. Torre and T. Poggio, "On edge detection," M.I.T. Artificial Intell. Lab., Cambridge, MA, Rep. AIM-768, 1984.
[29] S. Ullman, The Interpretation ofVisual Motion. Cambridge, MA: M.I.T. Press, 1979.
[30] N. Wiener, Extrapolation, Interpolation andSmoothing ofStationary Time Series. Cambridge, MA: M.I.T. Press, 1949.
[31] A. P. Witkin, "Shape from contour," M.I.T. Artificial Intell. Lab., Cambridge, MA, Rep. AI-TR-589, 1980.