Image Processing and Analysis_8_Edge Detection:Theory of Edge Detection ——1980
此主要讨论图像处理与分析。虽然计算机视觉部分的有些内容比如特 征提取等也可以归结到图像分析中来,但鉴于它们与计算机视觉的紧密联系,以 及它们的出处,没有把它们纳入到图像处理与分析中来。同样,这里面也有一些 也可以划归到计算机视觉中去。这都不重要,只要知道有这么个方法,能为自己 所用,或者从中得到灵感,这就够了。
8. Edge Detection
边缘检测也是图像处理中的一个基本任务。传统的边缘检测方法有基于梯度 算子,尤其是 Sobel 算子,以及经典的 Canny 边缘检测。到现在,Canny 边缘检 测及其思想仍在广泛使用。关于 Canny 算法的具体细节可以在 Sonka 的书以及 canny 自己的论文中找到,网上也可以搜到。最快最直接的方法就是看 OpenCV 的源代码,非常好懂。在边缘检测方面,Berkeley 的大牛 J Malik 和他的学生 在 2004 年的 PAMI 提出的方法效果非常好,当然也比较复杂。在复杂度要求不高 的情况下,还是值得一试的。MIT的Bill Freeman早期的代表作Steerable Filter 在边缘检测方面效果也非常好,并且便于实现。这里给出了几篇比较好的文献, 包括一篇最新的综述。边缘检测是图像处理和计算机视觉中任何方向都无法逃避 的一个问题,这方面研究多深都不为过。
[1980] theory of edge detection
[1983 Canny Thesis] find edge
[1986 PAMI] A Computational Approach to Edge Detection
[1990 PAMI] Scale-space and edge detection using anisotropic diffusion
[1991 PAMI] The design and use of steerable filters
[1995 PR] Multiresolution edge detection techniques
[1996 TIP] Optimal edge detection in two-dimensional images
[1998 PAMI] Local Scale Control for Edge Detection and Blur Estimation
[2003 PAMI] Statistical edge detection_ learning and evaluating edge cues
[2004 IEEE] Edge Detection Revisited
[2004 PAMI] Design of steerable filters for feature detection using canny-like criteria
[2004 PAMI] Learning to Detect Natural Image Boundaries Using Local Brightness, Color, and Texture Cues
[2011 IVC] Edge and line oriented contour detection State of the art
翻译
边缘检测理论——http://tongtianta.site/paper/32263#anchor_25
作者:D. MARR AND E. HILDRETH
请参阅本出版物的讨论,统计数据和作者简介:https://www.researchgate.net/publication/17083076
摘要 -提出了边缘检测理论。分析分为两部分。 (1)在不同尺度上分别检测在很大范围内的自然图像中发生的强度变化。在给定比例下用于此目的的适当滤波器被发现是高斯的二阶导数,并且示出了,只要满足一些简单条件,这些主滤波器不需要定向相关。因此,通过找到图像 I 的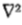 G(x,y)* I(x,y)的零值,可以最好地检测给定尺度的强度变化,其中G(x,y)是二维高斯分布和
G(x,y)* I(x,y)的零值,可以最好地检测给定尺度的强度变化,其中G(x,y)是二维高斯分布和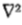 是拉普拉斯算子。然后,在每个通道中发现的强度变化由称为过零段的定向基元表示,并且证明该表示是完整的。 (2)图像中的强度变化来自表面不连续或来自反射或照明边界,并且这些都具有它们在空间上局部化的特性。因此,来自不同通道的过零段不是独立的,并且推导出将它们组合成图像描述的规则。此描述称为原始原始草图。该理论解释了几个基本的心理物理学发现,并且从作用于图像的中心环绕
是拉普拉斯算子。然后,在每个通道中发现的强度变化由称为过零段的定向基元表示,并且证明该表示是完整的。 (2)图像中的强度变化来自表面不连续或来自反射或照明边界,并且这些都具有它们在空间上局部化的特性。因此,来自不同通道的过零段不是独立的,并且推导出将它们组合成图像描述的规则。此描述称为原始原始草图。该理论解释了几个基本的心理物理学发现,并且从作用于图像的中心环绕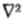 G 滤波器的输出形成定向过零段的操作形成了简单细胞的生理模型的基础(参见Marr&Ullman 1979)。
G 滤波器的输出形成定向过零段的操作形成了简单细胞的生理模型的基础(参见Marr&Ullman 1979)。
引言
Hubel&Wiesel(1962)和Campbell&Robson(1968)的实验引入了两个相当不同的概念,即早期信息处理在高级视觉系统中的功能。Hubel&Wiesel将简单细胞描述为线状的条状或边缘形状的感受野导致皮层视图包含一组特征检测器(Barlow 1969,第881页),调整到各种宽度和方向的边缘和条形。Campbell & Robson的实验表明,视觉信息是由许多独立的方向和空间频率调谐的频道并行处理的,这表明了一种截然不同的观点,它以极端的形式将视觉皮层描述为一种空间傅里叶分析仪(Pollen等,1971; Maffei& Fiorentini 1977)。
每一种观点的主角都能够对另一种观点提出实质性的批评。反对傅立叶解释的要点是:(1)通道的带宽不窄(1.6个八度,Wilson&Bergen 1979)。相应的感受野具有明确的空间定位。 (2)正如Campbell & Robson发现的那样,早期的视觉信息处理不是线性的(例如概率求和(Graham 1977; Wilson&Giese 1977)和叠加失败(Maffei&Fiorentini 1972 a))。 (3)只有基本的相位信息显然是编码的(Atkinson&Campbell 1974)。
反对线性特征检测器思想的要点是,如果一个简单的单元真实地发信号通知其条形感受野的线性卷积的正或负部分与图像强度,它很难被认为是一些关于图像中存在条形的象征性断言(Marr 1976a,p.648)。这种细胞必然响应比酒吧其他许多刺激,更大力,例如,到一个明亮的边缘比到昏暗巴,并且因此不会在它的响应,以保证被称为一个特征检测器足够特异性的。
也许两个阵营面临的最大困难是,这两种方法都无法直接提供有关图像早期分析目标的信息。这激发了一种新的视觉方法,它直接询问了视觉本身任务中固有的信息处理问题(Marr 1976a,b;并参见Marr 1978的整体方案)。根据该方案,早期视觉处理的目的是构造图像的原始但丰富的描述,该描述将用于确定可见表面的反射率和照度,以及它们相对于观察者的方向和距离。图像的第一个原始描述称为原始草图(Marr 1976b),它由两部分组成。首先,使用边缘段,条形图,斑点和终点的原始语言来描述图像中的强度变化。这种描述被称为原始的原始草图(Marr 1976b,p.497)。其次,几何关系是明确的(使用虚线),并且通过以各种方式选择,分组和概括原始基元来构造更大的,更抽象的标记。由此产生的描述层次涵盖了一系列尺度,称为图像的完整原始草图。
虽然原始草图的灵感来源于哺乳动物视觉系统的发现,但直到最*我们才无法将其作为人类早期视觉详细理论的基础。现在有三个发展使这成为可能:(a)关于早期人类视觉中存在的通道的定量信息的出现(Cowan 1977; Graham 1977; Wilson&Giese 1977; Wilson&Bergen 1979); (b)Marr&Poggio(1979)的人类视觉理论(特别是编写它的框架); (c)Marr等人的相关观察。 (1979)关于像Logan(1977)定理的结果与早期视觉的相关性。
这些进步使得制定令人满意的计算理论成为可能。本文讨论第一部分,原始原始草图的推导。理论本身分为两部分,第一部分涉及每个频道内的分析,第二部分则结合来自不同频道的信息。每个计算部分都讨论了实现的算法理论,并举例说明。
本文的后半部分探讨了对生物学的影响。算法的行为表明了一系列基本的心理学发现,并提出了一个特定的神经实现。我们的模型并不打算作为生理机制的完整建议,因为它忽略了方向选择性的特性,因此遍及皮质单纯细胞。然而,该模型确实明确了我们认为的某些非线性特征至关重要,它构成了Marr&Ullman(1979)更完整提案的起点,该方案结合了方向选择性。
检测和表示图像中的强度变化
自然图像的一个主要困难是变化可以并且确实发生在各种尺度上(Marr 1976a,b)。没有一个过滤器可以在所有尺度上同时最佳,因此应该寻求一种单独处理不同尺度发生的变化的方法。这一要求以及Campbell&Robson(1968)的研究结果得出了基本思想,如图1所示,其中一个首先采用不同分辨率的图像的局部*均值,然后检测每个分辨率发生的强度变化。一。为了实现这个想法,我们需要确定(a)最佳*滑滤波器的性质,以及(b)如何检测给定尺度的强度变化。
最佳*滑滤波器
有两个物理因素可以组合起来确定合适的*滑滤波器。首先,过滤图像的动机是减少发生强度变化的尺度范围。因此,滤波器的频谱应该在频域中*滑且频带受限。我们可以通过要求它的方差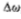 应该很小来表达这种情况。
应该很小来表达这种情况。
第二个考虑最好表示为空间域中的约束,我们称之为空间定位的约束。世界上引起图像强度变化的事物是:(1)照明变化,包括阴影,可见光源和照明梯度; (2)与可见表面的观察者的方向或距离的变化; (3)表面反射率的变化。这里的批判性观察是,按照自己的规模,这些东西都可以被认为是空间本地化的。除了偶尔的衍射图案外,视觉世界不是由波纹状的波状原始物构成的,它们在一个区域上延伸并加在一起(参见Marr 1970,第169页),但是轮廓,折痕,划痕,标记,阴影和(明暗)阴影。
我们对此约束的结果是,对滤波图像中每个点的贡献应来自附*点的*滑*均值,而不是广泛分散点的任何*均值。因此,我们寻找的滤波器也应该是*滑的并且在空间域中定位,特别是其空间方差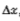 也应该是小的。
也应该是小的。

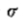 = 8个图像元素的高斯滤波图像,并且在(c)中,
= 8个图像元素的高斯滤波图像,并且在(c)中,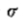 = 4.图像是320×320个图像元素。
= 4.图像是320×320个图像元素。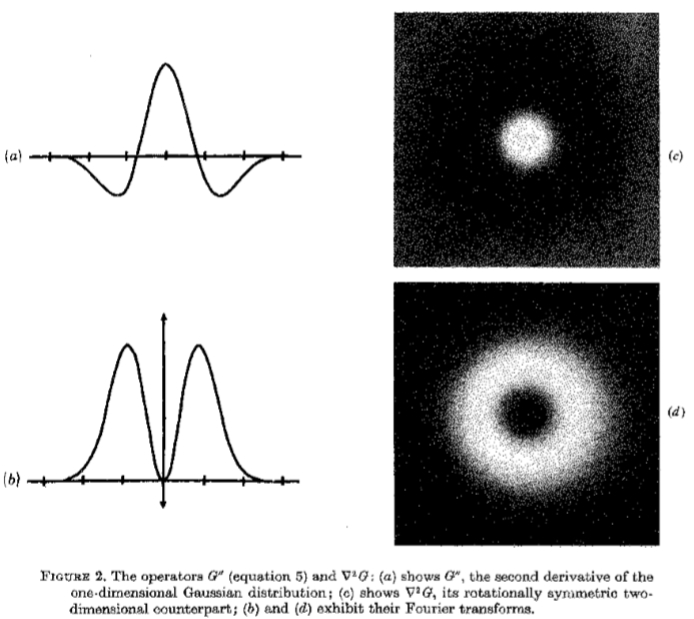
图2.运算符G“(等式5)和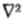 G:(a)表示G”,一维高斯分布的二阶导数; (c)显示
G:(a)表示G”,一维高斯分布的二阶导数; (c)显示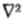 G,其旋转对称的二维对应物; (b)和(d)展示其傅立叶变换。
G,其旋转对称的二维对应物; (b)和(d)展示其傅立叶变换。
不幸的是,这两个本地化要求,即空间和频域中的要求是相互矛盾的。事实上,它们与不确定性原理有关,该原则指出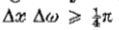 (例如,见Bracewell 1965,pp.160-163)。此外,只有一种分布可以优化这种关系(Leipnik 1960),即高斯分布
(例如,见Bracewell 1965,pp.160-163)。此外,只有一种分布可以优化这种关系(Leipnik 1960),即高斯分布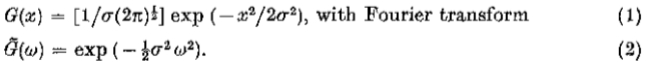
在二维中,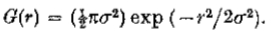
因此,过滤器G在我们的冲突要求之间提供了最佳的权衡。
检测强度变化
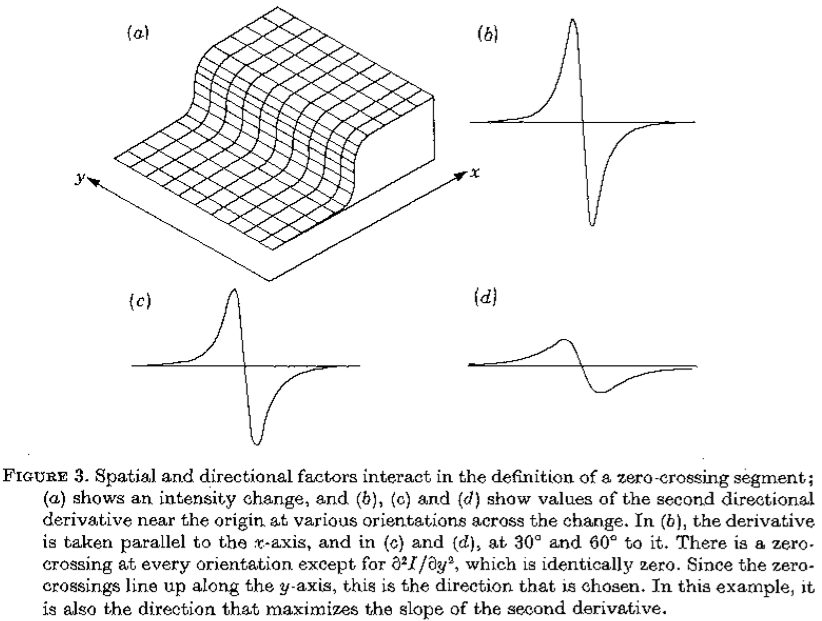
图3.空间和方向因素在过零段的定义中相互作用; (a)表示强度变化,(b),(c)和(d)表示在变化的各个方向上原点附*的第二方向导数的值。在(b)中,导数与x轴*行,在(c)和(d)中,在30度和60度 它。除了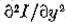 之外,每个方向都有一个过零点,它相同为零。由于零交叉沿y轴排列,因此这是所选择的方向。在这个例子中,它也是使二阶导数的斜率最大化的方向。
之外,每个方向都有一个过零点,它相同为零。由于零交叉沿y轴排列,因此这是所选择的方向。在这个例子中,它也是使二阶导数的斜率最大化的方向。
无论强度发生何种变化,在第一个方向导数中都会有一个相应的峰值,或者相当于第二个方向强度导数的过零点(Marr 1976b; Marr&Poggio 1979)。实际上,我们可以用这种方式定义强度变化,以便检测这些变化的任务可以减少到在适当的方向上找到强度的二阶导数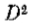 的过零点。也就是说,我们寻求零交叉
的过零点。也就是说,我们寻求零交叉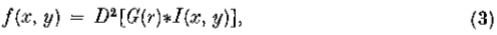
其中 I(x,y)是图像,*是卷积运算符。由衍生物—卷积规则,
我们可以将运算符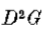 写为G“,并在一个维度上
写为G“,并在一个维度上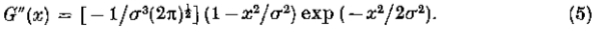
G“(x)看起来像墨西哥帽子操作员(见图2),它非常类似于Wilson S&Giese(1977)两个高斯(DOG)的差异,事实上,它是DOG功能的极限这两个高斯人彼此倾向(见图11和附录B)。它是*似带通运算符,半功率带宽约为1.2倍频程,因此可以将其视为查看图像频谱的一个特定部分中包含的信息。
这些论点确定原则上可以通过将图像与运算符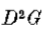 卷积并在其输出中寻找零交叉来检测一个尺度的强度变化。只有一个问题仍未解决,它涉及与
卷积并在其输出中寻找零交叉来检测一个尺度的强度变化。只有一个问题仍未解决,它涉及与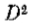 相关的方向。在任何方向上选择二阶导数的过零是不够的。要理解这一点,想象一下沿y轴向下的均匀强度变化,如图3所示。在原点,第二方向导数在每个方向上都是零,但除了沿y轴,它在每个方向上都是非零的。
相关的方向。在任何方向上选择二阶导数的过零是不够的。要理解这一点,想象一下沿y轴向下的均匀强度变化,如图3所示。在原点,第二方向导数在每个方向上都是零,但除了沿y轴,它在每个方向上都是非零的。
应该在哪个方向上采用衍生物?
为了选择使用哪个方向导数,我们观察到检测强度变化的潜在动机是它们将对应于物理世界的有用属性,例如反射率,照度,表面方向或距观察者的距离的变化。这些属性在空间上是连续的,并且几乎可以在任何地方与投射到图像中的方向的方向相关联。因此,我们选择使用的方向导数的方向与其零交叉局部形成的方向一致。在图3中,这个方向是y轴,因此我们选择的方向导数是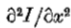 。
。
在什么条件下,这个方向与零交叉具有最大斜率的方向一致? 对此的答案由定理1给出(见附录A),我们称之为线性变化的条件:
零交叉线附*和*行的强度变化应该是线性的。
在*滑图像中,这种情况几乎是正确的,在本文的其余部分,我们将假设线性变化的条件成立。
这个方向可以通过拉普拉斯算子找到
检测过零点有三个主要步骤。它们是:(1)与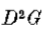 的卷积,其中
的卷积,其中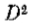 代表第二个方向导数运算。(2)零交叉的定位; (3)检查局部零交叉段的对齐和方向。虽然可以直接实施这一方案(Marr 1976b,p.494),但可以提出的一个直接问题是,这里的方向性衍生物至关重要吗? 卷积是相对昂贵的,并且如果可以减少它们的数量,例如通过仅使用一个与方向无关的运算符,它将大大减轻计算负担。
代表第二个方向导数运算。(2)零交叉的定位; (3)检查局部零交叉段的对齐和方向。虽然可以直接实施这一方案(Marr 1976b,p.494),但可以提出的一个直接问题是,这里的方向性衍生物至关重要吗? 卷积是相对昂贵的,并且如果可以减少它们的数量,例如通过仅使用一个与方向无关的运算符,它将大大减轻计算负担。
唯一的与方向无关的二阶微分算子是拉普拉斯算子 ,定理2(见附录A)明确了它可以使用的条件。它们比我们在定理1中遇到的线性变化条件弱,并且它们表明,如果
,定理2(见附录A)明确了它可以使用的条件。它们比我们在定理1中遇到的线性变化条件弱,并且它们表明,如果
(G * I)中的强度变化是线性的,但不一定接*过零线,那么零 - 将通过拉普拉斯算子的零值检测并准确定位交叉。同样,因为在我们的应用中,线性变化的条件大致满足,所以这种情况也是如此。因此,强度变化的检测可以基于滤波器 G,如图2所示。然而,值得记住的是,原则上,如果强度沿着非常非线性的方式沿着区段变化,则拉普拉斯算子以及操作符
G,如图2所示。然而,值得记住的是,原则上,如果强度沿着非常非线性的方式沿着区段变化,则拉普拉斯算子以及操作符 G将看到零交叉位移到一侧。
G将看到零交叉位移到一侧。
论点摘要
因此,到目前为止论证的主要步骤是这些。
(1)为了限制强度可以改变的速率,我们首先用二维高斯算子G对图像I进行卷积。
(2)然后,G * I中的强度变化由第二方向导数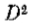 (G * I)中的过零点表征。 此运算符大致为带通,因此它仅检查图像的一部分频谱。
(G * I)中的过零点表征。 此运算符大致为带通,因此它仅检查图像的一部分频谱。
(3)应选择方向导数的方向,以与下面的过零线的局部方向一致。
(4)如果线性变化条件成立,则该方向也是过零点具有最大斜率(垂直于过零方向测量)的方向。
(5)根据附录A的定理1,如果线性变化的条件成立,则由(3)定义的过零线恰好是与方向无关的微分算子拉普拉斯算子 的过零点。
的过零点。
(6)因此,通过搜索卷积 G * I 的零值,可以在每个给定尺度的图像中经济地检测由(3)定义的过零点的轨迹。在二维中,
G * I 的零值,可以在每个给定尺度的图像中经济地检测由(3)定义的过零点的轨迹。在二维中,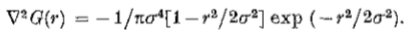
我们现在转向如何表示如此检测到的强度变化的问题。
代表强度变化
在带限图像中,变化*稳地发生,因此总是可以将零交叉线分成小段,每个段大致服从线性变化的条件。这一事实使我们能够做出以下定义。
(1)高斯滤波图像中的过零段由第二方向导数算子中零交叉的线性段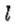 组成,其方向垂直于
组成,其方向垂直于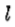 。
。
(2)我们还可以定义与过零段相关的幅度v,作为垂直于段的方向导数的斜率。为了理解为什么这是一个合适的测量,观察到原点过零点附*的窄带通道可以*似地用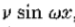 来描述,其在原点处具有斜率
来描述,其在原点处具有斜率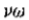 。因此,如果 s 是零交叉的测量斜率,则 v = s / w 。因子 1/ w 是空间常数,并且与所需的采样间隔成线性比例。
。因此,如果 s 是零交叉的测量斜率,则 v = s / w 。因子 1/ w 是空间常数,并且与所需的采样间隔成线性比例。
该组过零段连同它们的幅度构成了在图像光谱的一个区域内发生的变化的原始符号表示。 现在可以通过同时在足够数量的通道上应用分析来完全覆盖频谱。
最后,有理由相信图像的这种表示是完整的。Marr 等人(1979)注意到 Logan(1977)最*关于单倍频程带通信号的过零的定理表明,这种过零段的集合信息非常丰富。如果滤波器的带宽为八度或更小,它们实际上将包含有关滤波图像的完整信息。实际上, G滤波器的半灵敏度带宽约为1.75倍,这使得它超出了 Logan定理适用的范围。另一方面,如果我们添加有关过零点斜率的信息,情况可能更合适。在标准采样定理中,如果给出一阶导数和值,则采样密度可以减半(例如,参见 Bracewell 1978,pp.198-200 )。对于Logan(1977)定理来说,似乎可能是类似的扩展。 如果这是真的,那么其基本动机是物理的零交叉段实际上将为任意强度分布的恢复提供充分的基础。
G滤波器的半灵敏度带宽约为1.75倍,这使得它超出了 Logan定理适用的范围。另一方面,如果我们添加有关过零点斜率的信息,情况可能更合适。在标准采样定理中,如果给出一阶导数和值,则采样密度可以减半(例如,参见 Bracewell 1978,pp.198-200 )。对于Logan(1977)定理来说,似乎可能是类似的扩展。 如果这是真的,那么其基本动机是物理的零交叉段实际上将为任意强度分布的恢复提供充分的基础。
总之,那么,我们已经示出了如何通过 G运算器检测一个尺度的强度变化,并且可以通过定向的过零段及其幅度来表示它们(可能完全)。要检测所有比例的变化,只需要添加其他通道,例如如上所述,并且在每个中执行相同的计算。这些表示是原始原始草图中描述性图元的前体,并标记从图像的“分析”到“符号”分析的过渡。剩下的步骤是将来自不同通道的过零点组合成原始的“边缘”元素,本文后面将讨论此任务。
G运算器检测一个尺度的强度变化,并且可以通过定向的过零段及其幅度来表示它们(可能完全)。要检测所有比例的变化,只需要添加其他通道,例如如上所述,并且在每个中执行相同的计算。这些表示是原始原始草图中描述性图元的前体,并标记从图像的“分析”到“符号”分析的过渡。剩下的步骤是将来自不同通道的过零点组合成原始的“边缘”元素,本文后面将讨论此任务。
示例和评论


图4。借助于 G的过零检测的例子。行(a)显示了三个图像。图4.通过
G的过零检测的例子。行(a)显示了三个图像。图4.通过 G进行过零检测的例子。行(a)显示三个图像,行(b)显示其与图2的
G进行过零检测的例子。行(a)显示三个图像,行(b)显示其与图2的 G滤波器的卷积(w = 2o = 8),零由中间灰色表示。在行(c)中,正值显示为白色,负值显示为黑色;在行(d)中只出现零交叉。
G滤波器的卷积(w = 2o = 8),零由中间灰色表示。在行(c)中,正值显示为白色,负值显示为黑色;在行(d)中只出现零交叉。
图4显示了零交叉的一些示例。顶行显示图像,第二行显示与操作员 G的卷积,如图2所示。
G的卷积,如图2所示。
零在这里用中间灰色表示,因此非常正值显示为白色,非常负值显示为黑色。 在第三行中,所有正值均显示为白色,所有负值均为黑色,第四行仅显示零值的位置。 可以观察到,这些很好地描绘了图像中的可见边缘。 (有关详细信息,请参见图例。)仅将零值轨迹分解为定向线段。

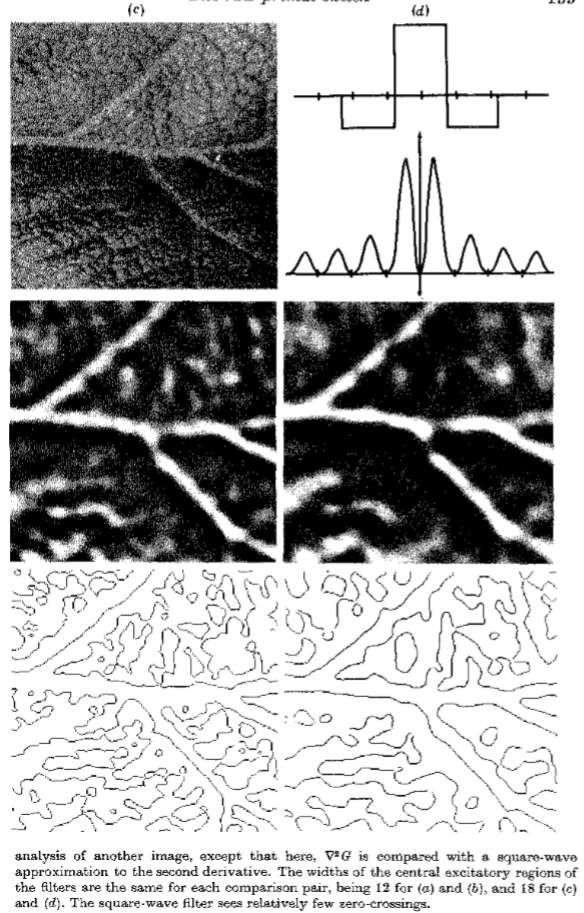
图5.  G与类似滤波器性能的比较。 列(a)显示了一个图像,它与a的卷积以及由此产生的有符号过零点。 列(b)包含相同的序列,但对于所示的纯单倍频带通滤波器,其傅里叶变换位于列的顶部。 过零阵列包含图像中强边缘的回波。 列(c)和(d)表现出对另一图像的相同分析,在此处,
G与类似滤波器性能的比较。 列(a)显示了一个图像,它与a的卷积以及由此产生的有符号过零点。 列(b)包含相同的序列,但对于所示的纯单倍频带通滤波器,其傅里叶变换位于列的顶部。 过零阵列包含图像中强边缘的回波。 列(c)和(d)表现出对另一图像的相同分析,在此处, G与对二阶导数的方波*似进行比较。 对于每个比较对,滤波器的中心激发区的宽度是相同的,对于(a)和(b)是12,对于(c)和(d)是18。 方波滤波器看到相对较少的过零点。
G与对二阶导数的方波*似进行比较。 对于每个比较对,滤波器的中心激发区的宽度是相同的,对于(a)和(b)是12,对于(c)和(d)是18。 方波滤波器看到相对较少的过零点。
有趣的是,比较通过 G找到的零交叉与通过类似算子找到的零交叉,根据我们的论点,这些操作不是最优的。我们对高斯滤波器的选择基于频率和空间域中的同时定位的要求。因此,我们举例说明严重违反了这些要求中的每一个。理想的单倍频程带通滤波器满足频域中的定位要求,但在空间域中违反了它。原因是严格的频带限制会在空间滤波器中产生旁瓣,其结果是,在过零图像中,强烈的强度变化会产生回波以及直接相应的过零点( 见图5)。 这些回波没有直接的物理相关性,因此不适合早期的视觉处理。
G找到的零交叉与通过类似算子找到的零交叉,根据我们的论点,这些操作不是最优的。我们对高斯滤波器的选择基于频率和空间域中的同时定位的要求。因此,我们举例说明严重违反了这些要求中的每一个。理想的单倍频程带通滤波器满足频域中的定位要求,但在空间域中违反了它。原因是严格的频带限制会在空间滤波器中产生旁瓣,其结果是,在过零图像中,强烈的强度变化会产生回波以及直接相应的过零点( 见图5)。 这些回波没有直接的物理相关性,因此不适合早期的视觉处理。
另一方面,如果切断空间域中的滤波器,则在频域中获取旁瓣。 图5还显示了二阶导数算子的方波*似,以及它产生的过零点的示例。 该运算符可以看到更少的过零点,主要是因为它*均了更广泛范围内发生的变化。
有趣的是,Rosenfeld&Kak(1976,pp.281-4)讨论了与'边缘'检测有关的拉普拉斯算子,但他们没有报告它的使用非常有效。其中一个原因是它不是非常有效,除非它在带限制的情况下使用并且使用其零交叉,并且这些想法没有出现在计算机视觉文献中(例如,参见Rosenfeld&Kak 1976 ,图10,关于如何使用拉普拉斯算子)。实际上,使用窄带通微分算子的想法直到 Marr&Poggio(1979)的人类立体理论才出现,这也是第一个主要依赖零交叉的理论。
另一个更实际的原因是“边缘检测”操作员以前在计算机视觉方面不是最佳成功,因为大多数现有操作员只检查图像的一小部分,他们的“感受野”大约为10到10 最多20个图像点。 这与威尔逊最小的四个心理物理通道形成鲜明对比,其中的感受野必须覆盖500多个中央凹视锥(见图4)。
最后,注意G“,因此 G,大约是二阶导数算子,因为它的傅立叶变换是
G,大约是二阶导数算子,因为它的傅立叶变换是 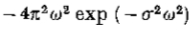 ,其行为类似于
,其行为类似于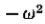 附*的原点。
附*的原点。
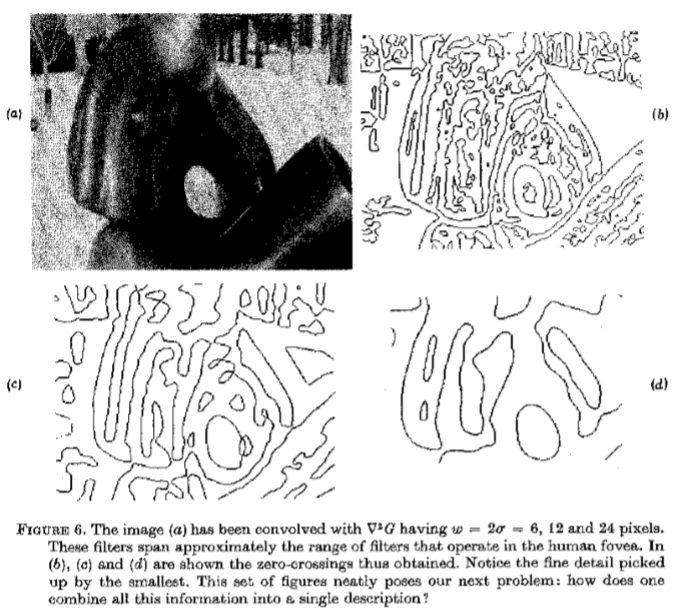
 G卷积,其中
G卷积,其中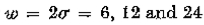 像素。这些过滤器大约跨越在人类中央凹中操作的过滤器范围。在(b)中,(c)和(d)显示了由此获得的过零点。请注意最小的细节。这组数字巧妙地提出了我们的下一个问题:如何将所有这些信息合并到一个描述中?
像素。这些过滤器大约跨越在人类中央凹中操作的过滤器范围。在(b)中,(c)和(d)显示了由此获得的过零点。请注意最小的细节。这组数字巧妙地提出了我们的下一个问题:如何将所有这些信息合并到一个描述中?
组合来自不同渠道的信息
除非基础信号受到约束,否则通过在傅里叶域中不重叠的信道发送的信号通常是不相关的。因此,我们这里的关键问题是(我们感谢 T.Poggio 关于这一点的对话的),当我们考虑如何组合来自不同渠道的信息以形成图像的原始描述时,需要考虑哪些附加信息?换句话说,视觉世界的结构是否存在任何一般的物理限制,使我们能够对来自不同频道的信息进行组合的方式施加有效限制? 图6说明了我们必须解决的问题。
空间重合假设
我们需要的附加信息来自空间定位的约束,我们在上一节中定义了这些约束。它指出,引起图像强度变化的物理现象在空间上是局部的。既然是这些变化那么。如果在滤波图像中产生过零点,则如果在以波长 为中心的信道中存在可辨别的过零点,则在波长
为中心的信道中存在可辨别的过零点,则在波长 的信道中的相同空间位置应该存在相应的过零点。如果在某个波长
的信道中的相同空间位置应该存在相应的过零点。如果在某个波长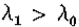 时这不再是真的,那将是出于以下两个原因之一:(a)两个或多个局部强度变化在较大的通道中被*均在一起;或(b)两个独立的物理现象用于在图像的同一区域产生强度变化但是在不同的尺度上。情况(a)的示例将是细条,其边缘将通过小通道而不是大通道精确定位。这种情况可以通过较小通道中存在两个附*的过零点来识别。情况(b)的一个例子是叠加在锐反射变化上的阴影,并且可以识别较大通道中的过零点是否相对于较小通道中的过零点移位。如果阴影具有正确的位置和方向,过零点的位置可能不包含足够的信息来分离这两种物理现象,但实际上,这种情况很少见。
时这不再是真的,那将是出于以下两个原因之一:(a)两个或多个局部强度变化在较大的通道中被*均在一起;或(b)两个独立的物理现象用于在图像的同一区域产生强度变化但是在不同的尺度上。情况(a)的示例将是细条,其边缘将通过小通道而不是大通道精确定位。这种情况可以通过较小通道中存在两个附*的过零点来识别。情况(b)的一个例子是叠加在锐反射变化上的阴影,并且可以识别较大通道中的过零点是否相对于较小通道中的过零点移位。如果阴影具有正确的位置和方向,过零点的位置可能不包含足够的信息来分离这两种物理现象,但实际上,这种情况很少见。
因此,我们可以基于以下假设对来自不同 通道的过零段集合进行解析,我们将其称为空间重合假设:
通道的过零段集合进行解析,我们将其称为空间重合假设:
如果在连续的大小范围内的一组独立 G信道中存在过零段,并且该段在每个信道中具有相同的位置和方向,则可以采用这种过零段的集合来指示由于单一物理现象(反射率,照明,深度或表面方向的变化)导致的图像强度变化的存在。
G信道中存在过零段,并且该段在每个信道中具有相同的位置和方向,则可以采用这种过零段的集合来指示由于单一物理现象(反射率,照明,深度或表面方向的变化)导致的图像强度变化的存在。
换句话说,假设来自相邻尺寸的独立通道的过零点重合,则它们可以合在一起。如果他们不这样做,他们可能来自不同的表面或物理现象。由此得出所需的最小信道数为2,并且如果两个信道在频域中合理地分开,并且它们的过零点一致,则可以采用组合的过零点来指示存在边缘。图片。
解析过零段的集合
图6显示了从两个通道获得的过零点,这两个通道的尺寸与人类视觉系统中心凹处存在的两个持续通道大致相同(Wilson&Bergen 1979)。 我们现在推导出组合来自不同通道的过零点所需的解析规则。
案例(1):孤立的边缘
对于孤立的,线性设置的强度变化,在一定尺寸以上的所有通道中存在相同取向的单个过零点,这取决于通道灵敏度和边缘的空间范围。因此,这组零交叉可以组合成一个符号,我们将其称为边缘段,具有边缘幅度和宽度的属性,我们可以如下获得。
边缘幅度的计算。 因为我们所做的假设意味着所涉及的强度变化的类型是一个简单的,我们实际上可以使用Marr(1976图1)所谓的选择标准,根据哪个选择最小的通道, 强度变化基本上与阶梯函数不可分割,并且仅使用该信道通过上面导出的幅度v来估计对比度。 如果只有两个具有幅度v和v2的独立通道,则边缘幅度的*似值为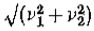 。
。
宽度的计算。在这种情况下,边缘的宽度也可以根据选择标准从所选择的信道估计。对于具有中心波长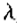 的窄通道,宽度的物理概念对应于强度增加的距离。该距离是
的窄通道,宽度的物理概念对应于强度增加的距离。该距离是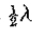 ,大约是w,与最激发的通道相关的感受野的中心兴奋区的宽度(实际上,
,大约是w,与最激发的通道相关的感受野的中心兴奋区的宽度(实际上,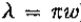 )。
)。
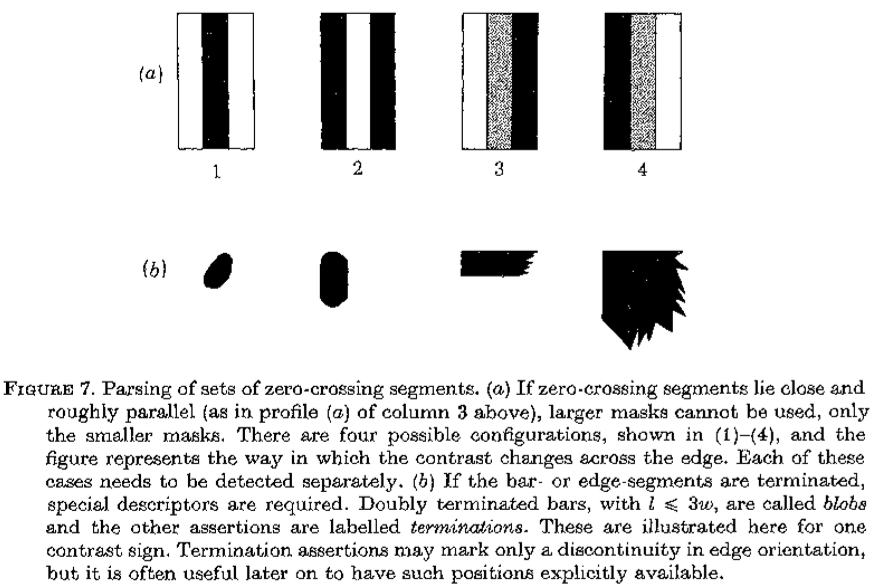
图7.解析过零段的集合。 (a)如果过零段靠*并大致*行(如上面第3栏的剖面(a)所示),则不能使用较大的掩模,只能使用较小的掩模。 有四种可能的配置,如(1) - (4)所示,该图表示对比度在边缘上的变化方式。 这些情况中的每一个都需要单独检测。 (b)如果条形或边条段终止,则需要特殊描述符。 l<3w 的双端终止条称为斑点,其他断言标记为终止。 这里示出了一个对比标志。 终止断言可以仅标记边缘方向的不连续性,但是稍后通常可以明确地获得这些位置。
案例(2):酒吧

如果具有相反对比度的两个*行边缘在图像中仅相隔小距离 d,则不能依赖来自具有超过约 2d 的相关波长的通道的过零点来提供关于边缘的位置或对比度的准确信息。 在这些情况下,必须忽略较大的信道,并且描述仅由过零段所叠加的小信道形成。 边缘可以具有正或负对比度,因此两者一起给出了图7a中所示的四种情况。 当然,没有理由为什么两个边缘应该具有相同的对比度,并且每个边缘的对比度必须从最小的通道(w <d)单独获得。 另外两个参数很有用; 一个是两个过零段的*均方向,另一个是它们的*均间隔。
我们的情况(2)仅适用于零交叉段都不会终止并且它们都保持大致*行(相隔很小 w 或更小)的情况。当最小可用信道的两个边缘比w更靠*时,与最小信道相关联的过零点将不能准确地反映两个边缘的位置,它们将过度估计它们之间的距离。如果两个边缘具有绝对幅度上没有太大差异的相反对比度,则在图像中如此形成的“线段”的中心位置将是两个相应过零点的中点。在这些情况下,与线段相关的参数将比与每个单独边缘相关的参数更可靠。
案例(3):斑点和终止
经常发生的是,零交叉段不会在图像上继续很远。 两个*行线段可以合并,或者由第三个线段连接,在纹理图像中,它们通常形成小的闭合曲线(见图6),与基础场尺寸相比,它们非常小。 这两种情况都可能在较大的通道尺寸上产生异常效应,因此最好在早期明确表示。 在Marr(1976b)之后,闭合的轮廓我们称之为斑点,并为它们分配长度,宽度,方向和(*均)对比度; 并且终端被分配位置和方向(见图7c)。
备注
我们的实施中出现了两个有趣的实用细节。首先,条形每个边缘处的强度变化实际上很少相同,因此将BAR描述符视为一个原始分组谓词可能更合适,它结合了两个边缘,其对比度由最小的渠道。当然,酒吧区域内的亮度是恒定的。其次,通常情况是来自小掩模和大掩模的过零点大致重合,但来自小掩模的过零点编织得更多,部分原因在于图像结构,部分原因是噪声和图像细分。局部方向对于短于 G滤波器中心兴奋区宽度w的距离没什么意义,因此,如果来自较小滤波器的过零点在局部快速改变方向,则从较大掩模得到的方向可以提供更稳定和更可靠的测量。
G滤波器中心兴奋区宽度w的距离没什么意义,因此,如果来自较小滤波器的过零点在局部快速改变方向,则从较大掩模得到的方向可以提供更稳定和更可靠的测量。
对生物学的影响
我们已经提出了构建原始原始草图的具体算法,现在我们要问人类视觉系统是否实现了这些算法或者它们附*的算法。我们的方案有两个经验可用的特征。第一个涉及潜在的卷积和零交叉段,第二个是来自不同渠道的过零段是否以我们描述的方式组合。
检测过零段
根据我们的理论,检测过零段的最经济的方法是首先通过至少两个独立的 G通道对图像进行滤波,然后在滤波后的输出中找到过零点。这些过零点可以分为短的,定向的过零段。
G通道对图像进行滤波,然后在滤波后的输出中找到过零点。这些过零点可以分为短的,定向的过零段。
经验数据
Wilson&Giese(1977),Wilson&Bergen(1979)(参见Macleod&Rosenfeld 1974)最*的心理物理学研究已经导致了坎贝尔和罗布森发现的取向依赖空间频率调谐通道的精确定量模型(1968)。 在视野中的每个点处,有四个这样的通道跨越大约三个八度音阶,并且它们的峰值灵敏度波长随着视网膜偏心率线性增加。 每个点的较大的两个通道是瞬态的,较小的两个通道是持续的。 这些通道可以通过线性单元实现,其具有由两个高斯分布的差异构成的条形接收场,对于持续的1:1.75和对于瞬态通道的比率为1:3.0,抑制空间常数具有兴奋性( Wilson&Bergen 1979)。 每个点的最大感受野大约是最小的四倍。
这种状态与神经生理学一致,因为Hubel&Wiesel(1962)最初通过其反应的线性来定义简单细胞,并且他们报告了许多条状感受野。此外,简单的细胞感受野大小随着偏心率线性增加(Hubel&Wiesel 1974,图6a),每个位置的尺寸分散似乎约为4:1(Hubel&Wiesel 1974,图7)。因此,很难用心理物理通道识别至少一些简单细胞。如果是这样,则进行识别的第一种明显方式是建议简单单元测量第二方向导数,从而可能提供随后检测到过零段的卷积值。
但是,有很多理由可以排除这一提议。
他们是:
(1)如果简单单元基本上执行*似第二方向导数的线性卷积,为什么它们如此方向敏感? 原则上,三次测量足以完全表征二阶导数,并且在实践中,沿着四个方向测量的方向导数对于该阶段显然是足够的(参见Marr 1976b; Hildreth,准备中),然而简单的细胞将域划分为 约12个方向。
(2)Schiller等(1976b,pp.1324-5)发现,单个细胞的方向敏感性相对独立于侧翼抑制的强度,以及感受野的正负场的分离和长度。 细胞。 此外,三方感受野似乎不比二分感受更敏感。 这些点提供了很好的证据,证明简单的细胞不是线性装置。
(3)如果简单单元执行卷积,那么哪些元素找到零交叉并实现计算的空间部分,例如,使用卷积方向将零交叉排列在上面?
Wilson的频道数据与 G一致
G一致
威尔逊的DOG功能与 G非常相似,并且可能通过他的实验技术无法区分,其准确率约为10%(H. G. Wilson,个人通信)。在附录B中,我们表明:(a)
G非常相似,并且可能通过他的实验技术无法区分,其准确率约为10%(H. G. Wilson,个人通信)。在附录B中,我们表明:(a) G是DOG函数的极限,即抑制与兴奋空间常数的比率趋于一致; (b)如果
G是DOG函数的极限,即抑制与兴奋空间常数的比率趋于一致; (b)如果 G的*似值是由两个高斯分布的差异构成的,一个是兴奋性的,另一个是抑制性的,那么
G的*似值是由两个高斯分布的差异构成的,一个是兴奋性的,另一个是抑制性的,那么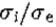 的工程理由的最佳选择是1.6左右。
的工程理由的最佳选择是1.6左右。
一个具体的建议:外侧膝状X细胞携带 G * I,一些简单的细胞检测并代表零交叉段
G * I,一些简单的细胞检测并代表零交叉段
已知视网膜神经节X细胞具有通过两个高斯分布的差异精确描述的感受野(Rodieck&Stone 1965; Ratliff 1965; Enroth-Cugell&Robson 1966)。正面和负面部分不是很*衡(对漫射照明有反应并且随着强度增加),并且由于神经节细胞具有自发静息放电,它们发出的信号不仅仅是正面或只是负面部分。卷积。有趣的是,在视网膜的给定位置,X细胞的感受野大小几乎没有分散(Peichl&Wassle 1979)。
关于外侧膝状体感受野的构建方式存在一些争议(参见Maffei&Fiorentini 1972b),但似乎最有可能的是,中心的膝状X细胞区是通过组合少数中心视网膜神经节X 细胞区域形成的,其中心大致重合(Cleland等人,197I) )。似乎可能以这种方式出现感受野大小的分散,因为考虑到心理物理学发现所需的散射量在 X和Y 通道中仅为两倍。最后,外侧膝状细胞对视网膜神经节细胞的扩散照射反应较小,有时根本没有反应(Hubel&Wiesel 196i)。
这些事实使我们得到了一个特别有吸引力的方案,为简单起见,我们以理想化的形式呈现。
(1) G的测量。可以认为持续的或X-细胞的膝状纤维携带
G的测量。可以认为持续的或X-细胞的膝状纤维携带 G* I 的正或负部分,其中图2的滤波器
G* I 的正或负部分,其中图2的滤波器 G在实践中通过高斯卷积算子与中心的差异来*似。围绕空间常数的比例为1:1.75。 (人们应该认为这是线性强度值的卷积,而不是它们的对数。原因是虽然视网膜中的神经信号是由 I /(I + K)复用的适应项。 ,其中 I 是入射光照和每受体每秒 K = 800 量子(Alpern等人,1970),在任何给定的图像中,最暗部分与最亮部分的比率很少超过25(局部比率约为30被视为一个光源(Ullman 1976)),并且在这样的范围内,这个函数不会偏离线性。)在视野中的每个点,有两种尺寸的滤波器(组合通道之间零交叉所需的最小值),这些对应于威尔逊和卑尔根(1979)的N和S通道。这两个通道的中心兴奋区域的宽度w的一维投影与中心凹处的3.1'和6.2'的偏心率线性地成比例。
G在实践中通过高斯卷积算子与中心的差异来*似。围绕空间常数的比例为1:1.75。 (人们应该认为这是线性强度值的卷积,而不是它们的对数。原因是虽然视网膜中的神经信号是由 I /(I + K)复用的适应项。 ,其中 I 是入射光照和每受体每秒 K = 800 量子(Alpern等人,1970),在任何给定的图像中,最暗部分与最亮部分的比率很少超过25(局部比率约为30被视为一个光源(Ullman 1976)),并且在这样的范围内,这个函数不会偏离线性。)在视野中的每个点,有两种尺寸的滤波器(组合通道之间零交叉所需的最小值),这些对应于威尔逊和卑尔根(1979)的N和S通道。这两个通道的中心兴奋区域的宽度w的一维投影与中心凹处的3.1'和6.2'的偏心率线性地成比例。
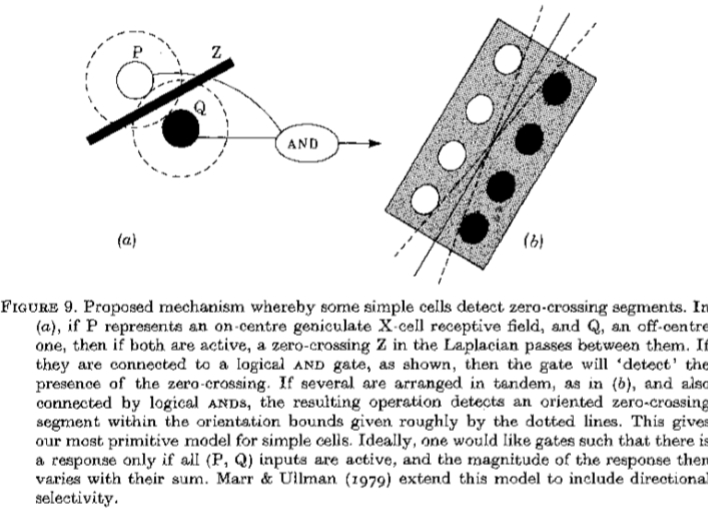
图9.一些简单单元检测过零段的建议机制。 在(a)中,如果P代表中心膝状X-细胞感受野,而Q代表偏心中心,那么如果两者都有效,则拉普拉斯算子中的过零Z在它们之间通过。 如果它们连接到逻辑AND门,如图所示,那么门将“检测”过零的存在。 如果多个串联布置,如(b)中那样,并且还通过逻辑ANDS连接,则所得到的操作检测在由粗线粗略给出的取向界限内的定向过零段。 这为简单单元格提供了最原始的模型。 理想情况下,人们希望门只有当所有(P,Q)输入都有效时才有响应,然后响应的幅度随其总和而变化。 Marr&Ullman(1979)扩展了这个模型,包括方向选择性。
我们的零交叉检测模型背后的基本思想取决于以下观察结果:如果一个中心的膝状细胞在位置P处于活动状态而一个偏心的细胞在附*的位置Q处于活动状态,那么 G的值*我在P和Q之间经过零(见图9a)。因此,通过逻辑AND运算组合来自P和Q的信号,可以构造运算符,用于检测过零段(在某个未知方位)何时在P和Q之间经过(图9a)。通过在纵向方向上添加非线性AND运算,可以以类似的方式构建检测定向过零段的运算符。很容易看出,图9b的纯逻辑运算符仅响应零交叉段,其取向位于其灵敏度范围内(粗略地示出)。因此,我们建议:
G的值*我在P和Q之间经过零(见图9a)。因此,通过逻辑AND运算组合来自P和Q的信号,可以构造运算符,用于检测过零段(在某个未知方位)何时在P和Q之间经过(图9a)。通过在纵向方向上添加非线性AND运算,可以以类似的方式构建检测定向过零段的运算符。很容易看出,图9b的纯逻辑运算符仅响应零交叉段,其取向位于其灵敏度范围内(粗略地示出)。因此,我们建议:
(2)过零段的检测和表示。 简单单元的一个子类的部分功能是检测过零段。 它们的反应领域包括图9b所示的结构,条件是非线性可能比那里显示的纯逻辑ANDS弱。 然而,该模型的一个关键特征是过零段上的(P和Q)相互作用(图9a)应包含强非线性分量和纵向相互作用(例如图9b中的末端之间) )至少包含弱非线性分量。Marr&Ullman (1979) 用于简单单元的完整模型包含该组织,但包括用于检测过零段的运动方向的附加机构,并且这为两个较大的瞬态通道提供了作用。
(3)信号幅度。理想情况下,单元的输出应由(2)的逻辑AND函数门控,但其值应为与沿段的过零点相关的*均局部幅度 v 。正如我们之前看到的,这可以通过测量零交叉的斜率的*均局部值来找到,其以(以合适的单位)等于到单元的输入的总和。
(4)采样密度。最后,为了使该方案成功,功能 G*I 的采样密度必须足够大,以确保零交叉随后可以准确地定位到足以解释关于超灵性的发现(例如,参见Westheimer& McKee) 1977),这意味着大约在 5' 之内。这意味着极高的表现精度,但在猴子纹状皮层的第四层,显然存在无数小的,中心环绕的,非定向细胞(Hubel&Wiesel 1968)。巴洛(1979)和克里克等人。 (1980)已经提出这些细胞可能参与V2G功能的重建,以达到足够的精确度。
G*I 的采样密度必须足够大,以确保零交叉随后可以准确地定位到足以解释关于超灵性的发现(例如,参见Westheimer& McKee) 1977),这意味着大约在 5' 之内。这意味着极高的表现精度,但在猴子纹状皮层的第四层,显然存在无数小的,中心环绕的,非定向细胞(Hubel&Wiesel 1968)。巴洛(1979)和克里克等人。 (1980)已经提出这些细胞可能参与V2G功能的重建,以达到足够的精确度。
Marr&Ullman(1979)提出了这一总体方案的实证结果。
零交叉的组合
心理物理学的经验预测
我们的算法有几个方面,用于组合来自不同通道的零交叉,可用于心理物理实验。它们是:(a)阶段关系; (b)来自不同渠道的过零点的组合,以及(c)过零点彼此靠*时产生的特殊情况。
(1)阶段关系。我们的理论预测描述符只需要存在于来自不同信道的零交叉集合,这些集合在空间上重合(即具有0或者相位关系)。有趣的是,阿特金森和坎贝尔(1974)叠加了相同方向的1和3周/度正弦光栅,并发现每分钟感知波动的数量(他们称之为单眼竞争率)在同相附*是低的,0 ,和异相,n,位置,但达到中间阶段位置的高原。他们得出结论(第161页),视觉系统包含一个'设计'似乎只能响应0和n相位关系的设备。什么时候。 [它] ..是活跃的,它产生一个稳定的感知,它是两个空间频率选择性通道的总和'(参见Maffei&Fiorentini 1972 a)。如果进一步假设存在明确表示通过组合适当排列的过零段而形成的边缘段描述符的单元,则我们的理论将预测这些结果。
(2)解析过程。这里的要点是描述。边缘(其宽度,幅度和方向)可以从(最小)通道获得,其过零点具有最大斜率。正如Marr(1976b,pp.496-497)所观察到的,这与Harmon&Julesz(1973)的发现一致,即与图像光谱相邻的噪声带在抑制识别方面最有效,因为它们对掩模的影响最大。重要掩模尺寸附*的响应幅度。它还解释了为什么从这样的图像中去除中间空间频率会在可见的格线背后留下可识别的林肯图像(参见Harmon&Julesz 1973)。原因是来自不同掩模尺寸的过零点不一致,并且光谱中的间隙意味着小条形描述符不能解释这种差异。因此,不能使用空间重合的假设,并且假设来自不同掩模尺寸的输出是由于不同的物理现象。因此,它们引起了独立的描述。
还有另一种可能但结果较弱的后果。如果做出额外的假设,那么选择标准是通过空间上重合并且在频域中相邻的过零段检测器之间的抑制连接来实现的,那么人们就会期望在皮层,方向上的通道之间找到抑制性相互作用。 - 依赖水*。事实上,有证据证明这种情况发生(参见,例如,Tolhurst 1972; de Valois 1977a)。
(3)条形探测器。 我们的解析算法的情况(2)需要特定检测*,*行,过零段。 这要求在每个方向上存在对四种情况中的一种敏感的单位(黑条,白条,两条暗边,两条光边)并且对它们的宽度(即分开边缘的距离)敏感而不是 到整个模式的空间频率特征。 最*发表了针对白条和黑条导致这些结论的适应性研究(Burton等人,1977; de Valois 1977b)。 如果我们的算法是由人类视觉系统实现的,那么类似的结果应该适用于其余两种情况(见图7a)。
(4)Blob检测器和终端。我们的解析算法的情况(3)需要(定向)斑点和终止的显式表示。重新呈现它们的单位应该易受心理物理适应的影响,事实上,Nakayama&Roberts(1972)和Burton&Ruddock(1978)已发现对长度不超过宽度三倍的棒材敏感的单位的证据。
神经生理学的后果
我们已经描述了实现解析过程的几种方法,但是直到我们从心理物理学中获得关于实际使用的解析算法的良好证据并且我们知道简单单元是否实际上,它们可能不值得详细设置。实现过零段的检测。如果没有这些信息,就无法做出公司预测,但我们提供以下建议作为神经实施的可能框架。 (1)四种类型的“条形”探测器可以在第一个简单的单元级别上实现(沿着图9的线,但是由三行中心环绕单元而不是两行)。 (2)对于相对孤立的边缘,应该存在定向边缘区段检测神经元,当这些区段在空间上重合时,并且仅当这些区段在空间上重合时,所述神经元组合来自不同通道的过零区段检测器(简单单元)。 (3)似乎已经发现了用于终端和斑点(双端接定向条)的探测器(Hubel&Wiesel 1962,1968)。有趣的是,Schiller等人。 (1976a)发现甚至一些简单的细胞也停止了。我们的方案与此一致,因为它需要在很早的阶段使用这种探测器。
讨论
“边缘”的概念具有部分视觉和部分物理意义。我们在本文中的主要目的之一是明确这种双重依赖:我们对边缘的定义轻微地依赖于关于方向导数的定理的早期假设,并且在很大程度上取决于空间定位的约束。
我们的理论基于两个主要思想。首先,通过在不同分辨率下分别处理图像,简化了强度变化的检测。然后,检测过程可以基于在二阶导数算子中找到零交叉,其实际上可以是(非定向的)拉普拉斯算子。此时的表示由过零段和它们的斜率组成。这种表示可能是完整的,因此原则上是可逆的。
之前只有Marr和R. Woodham的实证演示(见Marr 1978,图7)。将来自不同渠道的信息组合成单一描述的后续步骤依赖于该理论的第二个主要思想,我们将其构建为空间重合假设。物理边缘将在附*大小的通道中产生大致重合的过零点。空间重合假设断言这与此相反是正确的,即零交叉的重合是存在真实物理边缘的充分证据。 如果一个通道中的过零点与其他通道中的过零点不一致,则它们可能是由不同的物理现象引起的,因此需要从两个源中形成描述并保持一定程度的分离。
最后,一些简单的单元检测并表示过零段并且这是在不同尺度上同时执行的基本思想,对Marr&Poggio(1979)立体理论有一些启示。 根据各种神经生理学研究(Barlow等,1967; Poggio&Fischer,1978; von der Heydt等,1978),存在视差敏感的简单细胞。 这些单元的存在与我们的建议一致,即它们检测到零交叉段,但不是因为它们执行等效于方向导数的线性卷积,因为它是由需要的零交叉段提供的原始符号描述。 在图像之间匹配,而不是原始卷积值。
我们感谢K. Nishihara,T。Poggio和S. Ullman的启发性和有益的评论。这项工作是在人工智能实验室进行的,这是麻省理工学院的一项研究项目,部分由国防部高级研究计划局支持,由海军研究办公室监督,合同号为N00014-75-C -0643。 D. M.也得到N.S.F.的支持。合同号77-07569-MCS。
参考文献
Alpern, M., Rushton, W. A. H. & Torii, S. 1970 The size of rod signals. J. Physiol., Lond. 206, 193-208.
Atkinson, J. & Campbell, F. 1974 The effect of phase on the perception of compound gratings. Vision Res. 14, 159-162.
Barlow, H. B. 1969 Pattern recognition and the responses of sensory neurons. Ann. N.Y. Acad. Sci. 156, 872-881.
Barlow, H. B. 1979 Reconstructing the visual image in space and time. Nature, Lond. 279, 189-190.
Barlow, H. B., Blakemore, C. & Pettigrew, J. D. 1967 The neural mechanism of binocular depth discrimination. J. Physiol., Lond. 193, 327-342.
Bracewell, R. 1965 The Fourier transform and its applications. New York: MacGraw-Hill. Burton, G. J., Nagshineh, S. & Ruddock, K. H. 1977 Processing by the human visual system of the light and dark contrast components of the retinal image. Biol. Cybernetics 28, 1-9.
Burton, G. J. & Ruddock, K. H. 1978 Visual adaptation to patterns containing two- dimensional spatial structure. Vision Res. 18, 93-99.
Campbell, F. W. & Robson, J. G. 1968 Applications of Fourier analysis to the visibility of gratings. J. Physiol., Lond. 197, 551-556.
Cleland, B. G., Dubin, M. WV. & Levick, W. R. 1971 Sustained and transient neurones in the cat's retina and lateral geniculate nucleus. J. Physiol., Lond. 217, 473-496.
Cowan, J. D. 1977 Some remarks on channel bandwidths for visual contrast detection. Neurosci. Res. Prog. Bull. 15, 492-517.
Crick, F. H. C., Marr, D. & Poggio, T. 1980 An information processing approach to under- standing the visual cortex. To appear in the N.R.P. symposium The cerebral cortex (ed. F. O. Schmidt & F. G. Worden).
De Valois, K. K. 1977 a Spatial frequency adaptation can enhance contrast sensitivity. Vision Res. 17, 1057-1065.
De Valois, K. K. 1977b Independence of black and white: phase-specific adaptation. Vision Res. 17, 209-215.
Enroth-Cugell, C. & Robson, J. G. 1966 The contrast sensitivity of retinal ganglion cells of the cat. J. Physiol., Lond. 187, 517-552.
Graham, N. 1977 Visual detection of aperiodic spatial stimuli by probability summation among narrowband channels. Vision Res. 17, 637-652.
Harmon, L. D. & Julesz, B. 1973 Masking in visual recognition: effects of two-dimensional filtered noise. Science N.Y. 180, 1194-1197.
von der Heydt, R., Adorjani, Cs., Hanny, P. & Baumgartner, G. 1978 Disparity sensitivity and receptive field incongruity of units in the cat striate cortex. Exp. Brain Res. 31, 523-545.
Hubel, D. H. & Wiesel, T. N. 1961 Integrative action in the cat's lateral geniculate body. J. Physiol., Lond. 155, 385-398.
Hubel, D. H. & Wiesel, T. N. 1962 Receptive fields, binocular interaction and functional architecture in the cat's visual cortex. J. Physiol., Lond. 160, 106-154.
Hubel, D. H. & Wiesel, T. N. 1968 Receptive fields and functional architecture of monkey striate cortex. J. Physiol., Lond. 195, 215-243.
Hubel, D. H. & Wiesel, T. N. 1974 Uniformity of monkey striate cortex: a parallel relation- ship between field size, scatter, and magnification factor. J. comp. Neurol. 158, 295-306.
Kulikowski, J. J. & King-Smith, P. E. 1973 Spatial arrangement of line, edge, and grating detectors revealed by subthreshold summation. Vision Res. 13. 1455-1478.
Leipnik, R. 1960 The extended entropy uncertainty principle. Inf. Control 3, 18-25.
Logan, B. F. Jr 1977 Information in the zero-crossings of bandpass signals. Bell Syst. tech. J. 56. 487-510.
Macleod, I. D. G. & Rosenfeld, A. 1974 The visibility of gratings: spatial frequency channels or bar-detecting units? Vision Res. 14, 909-915.
Maffei, L. & Fiorentini, A. 1972a Process of synthesis in visual perception. Nature, Lond. 240, 479-481.
Maffei, L. & Fiorentini, A. 1972b Retinogeniculate convergence and analysis of contrast. J. Neurophysiol. 35, 65-72.
Maffei, L. & Fiorentini, A. 1977 Spatial frequency rows in the striate visual cortex. Vision Res. 17, 257-264.
Marr, D. 1970 A theory for cerebral neocortex. Proc. R. Soc. Lond. B 176, 161-234.
Marr, D. 1976a Analyzing natural images: a computational theory of texture vision. Cold Spring Harbor Symp. quant. Biol. 40, 647-662.
Marr, D. 1976b Early processing of visual information. Phil. Trans. R. Soc. Lond. B 275, 483-524.
Marr, D. 1978 Representing visual information. A.A.A.S. 143rd Annual Meeting, Sym- posium on: Some mathematical questions in biology, February 1977. Published in Lectures on mathematics in the life sciences 10, 101-180. Also available as M.I.T. A.I. Lab.Memo 415.
Marr, D. & Poggio, T. 1979 A computational theory of human stereo vision. Proc. R. Soc. Lond. B 204, 301-328.
Marr, D., Poggio, T. & Ullman, S. 1979 Bandpass channels, zero-crossings, and early visual information processing. J. opt. Soc. Am. 69, 914-916.
Marr, D. & Ullman, S. 1979 Directional selectivity and its use in early visual processing. (In preparation.)
Mayhew, J. E. W. & Frisby, J. P. 1978 Suprathreshold contrast perception and complex random textures. Vision Res. 18, 895-897.
Nakayama, K. & Roberts, D. J. 1972 Line-length detectors in the human visual system: evidence from selective adaptation. Vision Res. 12, 1709-1713.
Peichl, L. & Wassle, H. 1979 Size, scatter and coverage of ganglion cell receptive field centres in the cat retina. J. Physiol., Lond. 291, 117-141.
Poggio, G. F. & Fischer, B. 1978 Binocular interaction and depth sensitivity of striate and prestriate neurons of the behaving rhesus monkey. J. Neurophysiol. 40, 1392-1405.
Pollen, D. A., Lee, J. R. & Taylor, J. H. 1971 How does the striate cortex begin the recon- struction of the visual world? Science N.Y. 173, 74-77.
Ratliff, F. 1965 Mach bands: quantitative studies on neural networks in the retina. San Francisco: Holden-Day.
Rodieck, R. W. & Stone, J. 1965 Analysis of receptive fields of cat retinal ganglion cells. J. Neurophysiol. 28, 833-849.
Rosenfeld, A. & Kak, A. C. 1976 Digital picture processing. New York: Academic Press. Sachs, M. B., Nachmias, J. & Robson, J. G. 197I Spatial-frequency channels in human vision. J. opt. Soc. Am. 61, 1176-1186.
Shapley, R. M. & Tolhurst, D. J. 1973 Edge detectors in human vision. J. Physiol., Lond. 229, 165-183.
Schiller, P. H., Finlay, B. L. & Volman, S. F. 1976a Quantitative studies of single-cell properties in monkey striate cortex. I. Spatiotemporal organization of receptive fields. J. Neurophysiol. 39, 1288-1319.
Schiller, P. H., Finlay, B. L. & Volman, S. F. 1976b Quantitative studies of single-cell properties in monkey striate cortex. II. Orientation specificity and ocular dominance. J. Neurophysiol. 39, 1320-1333.
Ullman, S. 1976 On visual detection of light sources. Biol. Cybernetics 21, 205-212. Westheimer, G. & McKee, S. P. 1977 Spatial configurations for visual hyperacuity. Vision Res. 17, 941-947.
Wilson, H. R. & Bergen, J. R. 1979 A four mechanism model for spatial vision. Vision Res. 19, 19-32.
Wilson, H. R. & Giese, S. C. 1977 Threshold visibility of frequency gradient patterns. Vision Res. 17. 1177-1190.
附录A
理论1
让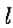 成为y轴的开放线段,包含原点0。假设
成为y轴的开放线段,包含原点0。假设 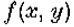 是连续可微的两次,并且N(l)是1个开放二维邻域。假设
是连续可微的两次,并且N(l)是1个开放二维邻域。假设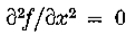 on
on 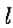 .然后,如果
.然后,如果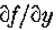 在N(
在N(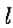 )中是常数),垂直于
)中是常数),垂直于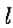 的第二方向导数的斜率(即,
的第二方向导数的斜率(即,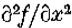 的斜率)大于沿着通过O的任何其他线的过零的斜率。
的斜率)大于沿着通过O的任何其他线的过零的斜率。
证明
考虑固定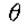 的线段
的线段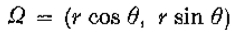 和 r 的值足够小,使得
和 r 的值足够小,使得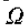 完全位于N(
完全位于N(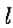 )内(见图10)。 现在为
)内(见图10)。 现在为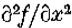 等编写
等编写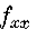 ,我们有
,我们有
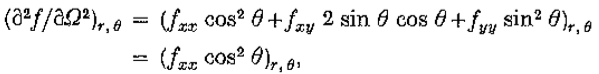
因为定理的条件是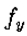 是常数意味着
是常数意味着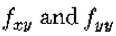 都是零。因此,根据需要,上述量在r = 0时为零,并且在
都是零。因此,根据需要,上述量在r = 0时为零,并且在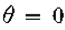 时具有最大斜率。
时具有最大斜率。
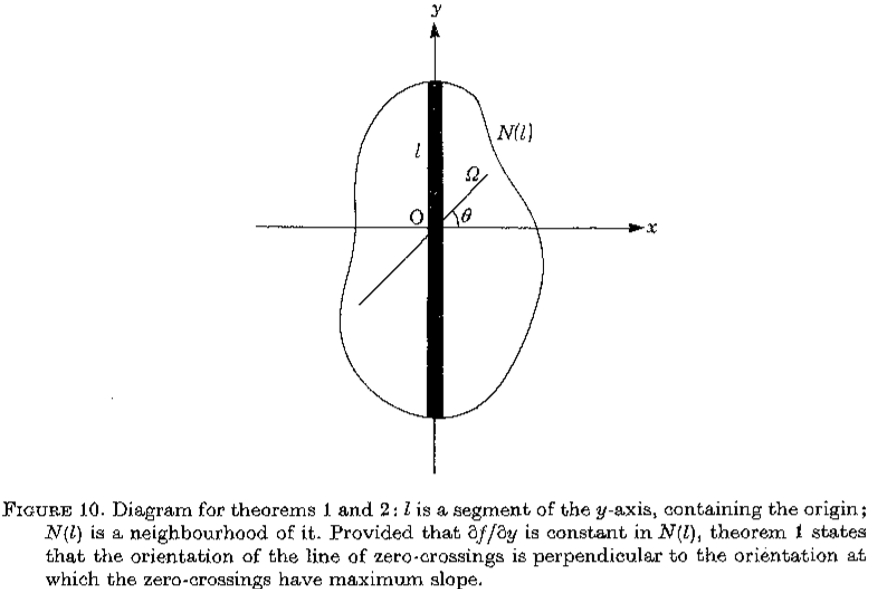
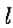 是y轴的一段,包含原点; N(
是y轴的一段,包含原点; N(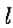 )是它的邻域。假设
)是它的邻域。假设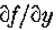 在 N(
在 N(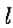 )中是常数,则定理1表明零交叉线的方向垂直于零交叉具有最大斜率的方向。
)中是常数,则定理1表明零交叉线的方向垂直于零交叉具有最大斜率的方向。
理论2
设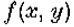 是*面上的实值,两次连续可微函数。 让
是*面上的实值,两次连续可微函数。 让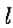 成为沿轴x = 0的开放线段。然后是两个条件
成为沿轴x = 0的开放线段。然后是两个条件
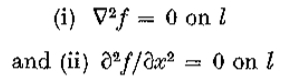
当且仅当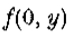 在
在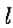 上是常数或线性时,它是等价的。
上是常数或线性时,它是等价的。
证明
如果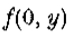 在
在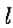 上是线性的,则
上是线性的,则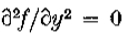 在
在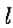 上。因此,
上。因此,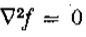 ,意味着
,意味着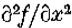 在
在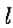 也是0。
也是0。
相反,如果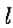 上的
上的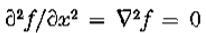 ,则
,则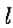 上的
上的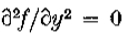 ,因此
,因此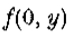 在
在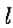 上最多线性变化。
上最多线性变化。
附录B.
DOG和V2G
V2G是DOG的限制
威尔逊的DOG功能可以写成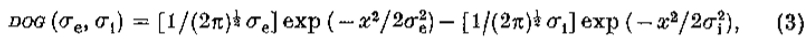
其中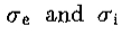 是兴奋性和抑制性空间常数。写
是兴奋性和抑制性空间常数。写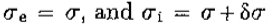 ,右手边随之变化
,右手边随之变化
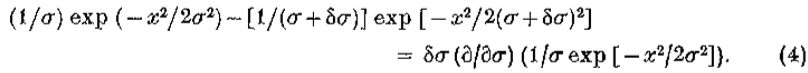
该导数等于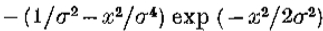 ,等于 G“ 直到常数(文本等式5)。)
,等于 G“ 直到常数(文本等式5)。)
DOG逼*V2G
函数: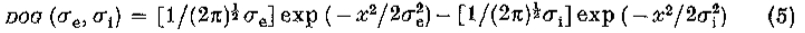
有傅里叶变换
请注意,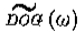 对
对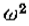 的值的行为类似于 w ,与
的值的行为类似于 w ,与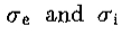 相比较小,因此这些过滤器与
相比较小,因此这些过滤器与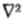 G一样,接*二阶导数算子。
G一样,接*二阶导数算子。
使用DOG逼*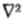 G的问题是找到一个空间常数,它可以使滤波器的带宽保持较小,同时又允许滤波器具有足够的灵敏度:因为,当空间常数彼此接*时,兴奋性的贡献很明显。和抑制成分变得相同,并且滤波器的灵敏度降低。
G的问题是找到一个空间常数,它可以使滤波器的带宽保持较小,同时又允许滤波器具有足够的灵敏度:因为,当空间常数彼此接*时,兴奋性的贡献很明显。和抑制成分变得相同,并且滤波器的灵敏度降低。
半灵敏度和半功率带宽以及峰值灵敏度都取决于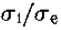 的值,如图11所示。由此可见:(i)半灵敏度带宽增长非常缓慢 高达约
的值,如图11所示。由此可见:(i)半灵敏度带宽增长非常缓慢 高达约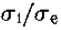 = 1.6,从那里增加到更快到
= 1.6,从那里增加到更快到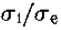 = 3.0,此后大致恒定; (ii)过滤器的峰值灵敏度对于小
= 3.0,此后大致恒定; (ii)过滤器的峰值灵敏度对于小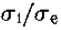 是无序的,在
是无序的,在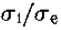 = 1.6时达到约33%。 由于我们的目标是创建一个窄带通差分运算符,我们应该选择
= 1.6时达到约33%。 由于我们的目标是创建一个窄带通差分运算符,我们应该选择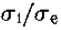 来最小化带宽。 由于
来最小化带宽。 由于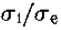 <1.6 时带宽*似恒定,并且由于灵敏度较低,实际选择的最小值约为1.6,提供1.8倍频程的半灵敏度带宽和
<1.6 时带宽*似恒定,并且由于灵敏度较低,实际选择的最小值约为1.6,提供1.8倍频程的半灵敏度带宽和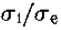 半功率带宽 1.3个八度音阶。
半功率带宽 1.3个八度音阶。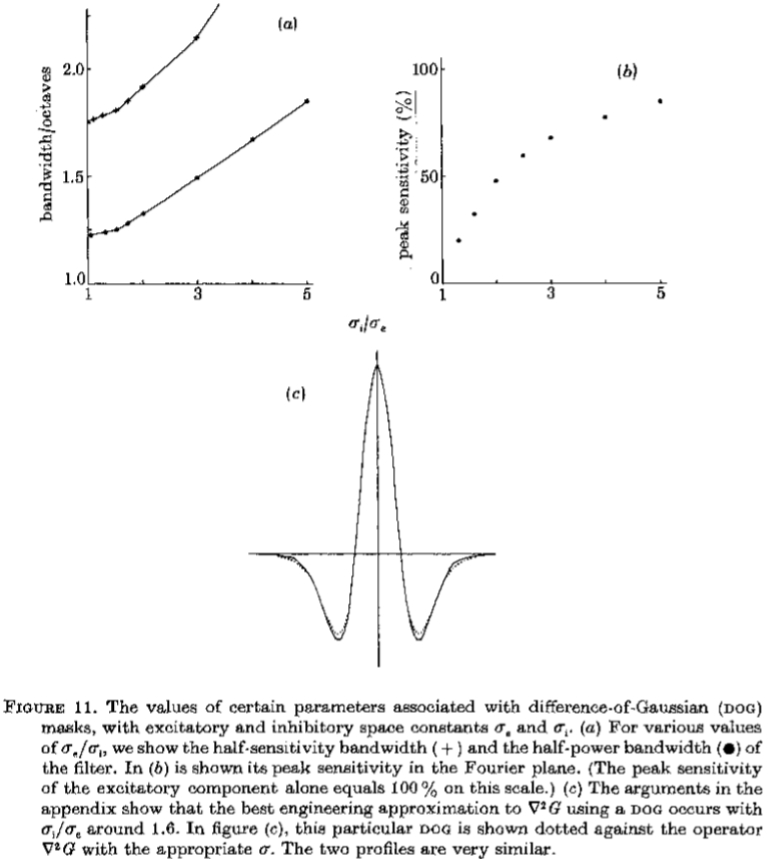
图11.与高斯差分(DOG)掩模相关的某些参数的值,具有兴奋性和抑制性空间常数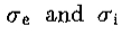 。 (a)对于各种
。 (a)对于各种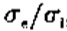 值,我们显示了滤波器的半灵敏度带宽(+)和半功率带宽
值,我们显示了滤波器的半灵敏度带宽(+)和半功率带宽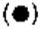 。在(b)中显示了其在傅里叶*面中的峰值灵敏度。 (在这个尺度上,兴奋性成分的峰值灵敏度单独等于100%。)(c)附录中的论据表明,使用DOG对
。在(b)中显示了其在傅里叶*面中的峰值灵敏度。 (在这个尺度上,兴奋性成分的峰值灵敏度单独等于100%。)(c)附录中的论据表明,使用DOG对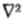 G的最佳工程*似发生在
G的最佳工程*似发生在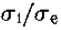 约1.6。在图(c)中,这个特定的DOG用适当的
约1.6。在图(c)中,这个特定的DOG用适当的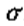 点缀在操作员
点缀在操作员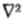 G上。这两个配置文件非常相似。
G上。这两个配置文件非常相似。
posted on 2019-09-18 16:03 Alliswell_WP 阅读(500) 评论(0) 编辑 收藏 举报



