Computer Vision_33_SIFT:PCA-SIFT A More Distinctive Representation for Local Image Descriptors——2004
此部分是计算机视觉部分,主要侧重在底层特征提取,视频分析,跟踪,目标检测和识别方面等方面。对于自己不太熟悉的领域比如摄像机标定和立体视觉,仅仅列出上google上引用次数比较多的文献。有一些刚刚出版的文章,个人非常喜欢,也列出来了。
33. SIFT
关于SIFT,实在不需要介绍太多,一万多次的引用已经说明问题了。SURF和PCA-SIFT也是属于这个系列。后面列出了几篇跟SIFT有关的问题。
[1999 ICCV] Object recognition from local scale-invariant features
[2000 IJCV] Evaluation of Interest Point Detectors
[2006 CVIU] Speeded-Up Robust Features (SURF)
[2004 CVPR] PCA-SIFT A More Distinctive Representation for Local Image Descriptors
[2004 IJCV] Distinctive Image Features from Scale-Invariant Keypoints
[2010 IJCV] Improving Bag-of-Features for Large Scale Image Search
[2011 PAMI] SIFTflow Dense Correspondence across Scenes and its Applications
翻译
PCA-SIFT对本地图像描述符的更具特色的表示——http://tongtianta.site/paper/56809
作者:Yan Ke, Rahul Sukthankar
——http://www.cs.cmu.edu/˜yke/pcasift/
摘要 -稳定的局部特征检测和表示是许多图像配准和对象识别算法的基本组成部分。Mikolajczyk和Schmid [14]最近评估了多种方法,并将SIFT [11]算法确定为对常见图像变形最有抵抗力的算法。本文研究(并改进了)SIFT使用的本地图像描述符。与SIFT相似,我们的描述符对特征点附近的图像梯度的显着方面进行编码;但是,我们没有使用SIFT的平滑加权直方图,而是将主成分分析(PCA)应用于归一化梯度补丁。我们的实验表明,与标准SIFT表示相比,基于PCA的局部描述符更具特色,对图像变形更鲁棒并且更紧凑。我们还提供了结果,表明在图像检索应用程序中使用这些描述符会提高准确性和加快匹配速度。
1.简介
局部描述符[6、12、18]通常在许多实际应用中使用,例如对象识别[3、11]和图像检索[13],因为它们可以高效地计算,抗部分遮挡并且是对观点的变化相对不敏感。在这些应用程序中使用本地描述符有两个注意事项。首先,我们必须定位兴趣点的位置和规模。通常,将兴趣点放置在标度空间搜索中的局部峰值处,并过滤以仅保留那些在转换后可能保持稳定的兴趣点。其次,我们必须对兴趣点进行描述;理想情况下,此描述应该与众不同(可靠地将一个兴趣点与其他兴趣点区分开),简洁明了,并且不会因相机姿势和照明的变化而引起变化。虽然兴趣点算法的定位和描述方面通常一起设计,但是这两个问题的解决方案是独立的[14]。本文关注于第二个方面的方法-局部描述符表示的构建和评估。
Mikolajczyk和Schmid [14]对几种局部描述符进行了比较研究,包括可控滤波器[4],微分不变量[9],矩不变量[18],复数滤波器[16],SIFT [11]和不同变量的互相关兴趣点的类型[6,13]。他们的实验表明,不同算法的准确度等级对在图像中找到兴趣点的方法相对不敏感,但是取决于用于对兴趣点周围的图像补丁进行建模的表示形式。由于使用SIFT描述符获得了最佳匹配结果,因此本文重点介绍该算法,并探索其局部描述符表示的替代方法。
本文的其余部分安排如下。第2节回顾了SIFT算法的相关方面。第3节详细介绍了我们基于PCA的本地特征表示(PCA-SIFT)。第4节介绍了我们的评估方法和绩效指标。第5节提供了在特征匹配实验以及图像检索应用程序中将PCA-SIFT与标准SIFT进行比较的详细实验结果。第6部分通过探讨表示中不同组件的作用,研究了PCA-SIFT准确性背后的原因。最后,第7节总结了本文的贡献。
2.审查(回顾)SIFT算法
如[12]所述,SIFT包括四个主要阶段:(1)标度-空间峰选择; (2)关键点本地化; (3)方向分配; (4)关键点描述符。在第一阶段,通过在位置和比例上扫描图像来识别潜在的兴趣点。这可以通过构造高斯金字塔并在一系列高斯差分(DoG)图像中搜索局部峰值(称为关键点)来有效地实现。在第二阶段,将候选关键点定位到亚像素精度,如果发现不稳定,则将其消除。第三部分根据每个关键点的局部图像补丁识别主要方向。为每个关键点分配的方向,比例和位置使SIFT可以为关键点构造一个标准视图,该视图对于相似性变换是不变的。最后阶段根据每个关键点的局部邻域中的图像梯度构建一个局部图像描述符(下面将详细讨论)。由于我们的工作对这三个领域没有任何贡献,因此本文将不讨论前三个阶段。
SIFT算法的最终(关键点描述符)阶段基于其局部邻域中的像素补丁为每个关键点构建表示。请注意,补丁以前曾以关键点的位置为中心,并根据其主要方向旋转并缩放到适当的大小。目标是为补丁创建一个描述符,该描述符紧凑,高度独特(即,来自不同关键点的补丁映射到不同的表示形式),并且对照明和相机视点的变化具有鲁棒性(即,不同图像中的相同关键点映射到相似的图像)表示)。如[12]中讨论的那样,诸如图像补丁之间的归一化相关性之类的明显方法不起作用,因为它们对套准误差和非刚性变形过于敏感。SIFT使用的标准关键点描述符是通过采样关键点周围补丁中图像梯度的大小和方向,并构建平滑的方向直方图来捕获补丁的重要方面而创建的。一个4×4的直方图阵列,每个直方图都有8个定向条,捕获了该补丁的大致空间结构。然后将此128个元素的向量归一化为单位长度,并设定阈值以删除具有较小值的元素。
标准的SIFT关键点描述符表示形式在几个方面值得关注:(1)表示形式经过精心设计,可以避免边界效应引起的问题-位置,方向和比例的平滑变化不会引起特征向量的根本变化; (2)它非常紧凑,使用128元素矢量表示像素点; (3)虽然并没有明确地改变到细微的变换,但这种表示却令人惊讶地对诸如透视效应引起的变形具有弹性。这些特性在针对竞争算法的出色匹配性能中得到了证明[14]。
另一方面,标准SIFT特征向量的构造很复杂,其具体设计(如[12]所述)背后的选择尚不清楚。我们的最初目标是探索更简单的替代方案,并根据经验评估权衡。但是,正如本文其余部分所讨论的,我们发现我们的替代表示在理论上比标准SIFT描述符更简单,更紧凑,更快,更准确。为了确保我们的结果能正确反映现实,我们使用原始的SIFT源代码并将更改限制在第四阶段。
3.基于PCA的SIFT描述符
我们的局部描述符算法(称为PCA-SIFT)接受与标准SIFT描述符相同的输入:关键点的子像素位置,比例和主要方向。我们以给定的比例提取一个41×41色块,以关键点为中心,旋转以将其主要方向与规范方向对齐。1 PCA-SIFT可以归纳为以下步骤:(1)将本征空间预先计算为表达局部补丁的梯度图像; (2)给定补丁,计算其局部图像梯度; (3)使用特征空间投影梯度图像向量,以得出紧凑特征向量。该特征向量比标准SIFT特征向量小得多,并且可以与相同的匹配算法一起使用。两个特征向量之间的欧式距离用于确定两个向量是否对应于不同图像中的相同关键点。
1对于具有多个主导方向的关键点,我们以与SIFT相同的方式为每个方向构建表示。
主成分分析(PCA)[7]是降维的一种标准技术,已被应用于广泛的计算机视觉问题,包括特征选择(例如[5]),对象识别(例如[15])和人脸识别(例如[17])。尽管PCA有许多缺点[8,10],例如其对高斯分布的隐含假设以及对正交线性组合的限制,但由于其简单性,它仍然很受欢迎。将PCA应用于图像补丁的想法并不新颖(例如[3])。我们的贡献在于严格证明PCA非常适合表示关键点补丁(一旦将它们转换为规范的比例尺,位置和方向),并且这种表示方式显着提高了SIFT的匹配性能。以下小节将详细介绍PCA-SIFT。
3.1 斑块特征空间的精细计算
PCA使我们能够将高维样本线性投影到低维特征空间上。对于我们的应用程序,此投影(由面片特征空间编码)可以预先计算一次并存储。
如上所述,输入向量是通过将以关键点为中心的41×41色块的水平和垂直渐变图进行级联来创建的。因此,输入向量具有2×39×39 = 3042个元素。然后,我们将此向量归一化为单位大小,以最小化照明变化的影响。重要的是要注意,41×41色块不跨越像素值的整个空间,也不是从自然图像中提取的较小色块。它由一系列严格限制的补丁组成,这些补丁通过了SIFT的前三个阶段。更准确地说,每个面片都满足以下特性:(1)它以比例空间的局部最大值为中心; (2)已旋转,使其(其中一个)主梯度方向对齐为垂直; (3)它仅包含适合此关键点的比例尺的信息-即41×41色块可能是从原始图像的更大区域创建的。输入向量中的其余变化主要是由于关键点的“身份”(即与该位置相对应的3D场景)或未建模的失真(例如,由于更改相机视点而导致的透视效果)。可以合理地相信,这些剩余的变化可以通过低维高斯分布合理地建模,从而使PCA可以使用紧凑的特征表示来准确地表示它们。更重要的是,将梯度贴片投影到低维空间上似乎可以保留与身份相关的变化,同时丢弃其他效应引起的失真。该假设得到第4节和第6节中讨论的实验证据的支持。
为了构建本征空间,我们在不同的图像集合上运行了SIFT算法的前三个阶段,并收集了21,000个色块。如上所述对每个进行处理以创建3042个元素的向量,并将PCA应用于这些向量的协方差矩阵。由前n个特征向量组成的矩阵存储在磁盘上,并用作PCA-SIFT的投影矩阵。建立本征空间的图像被丢弃,没有用于任何匹配实验。
3.2 特征表示
为了找到给定图像补丁的特征向量,我们只需创建其3042个元素的归一化图像梯度向量,然后使用存储的特征空间将其投影到我们的特征空间中即可。我们根据经验确定了特征空间维数n的良好值;本文描述的大多数结果都使用n=20(第6节讨论了n对性能的影响)。标准的SIFT表示采用128个元素的向量;使用PCA-SIFT会带来巨大的空间收益。
如上所述,我们使用两个特征向量之间的欧式距离来确定两个向量在不同图像中是否属于同一关键点。将此阈值设置为阈值可生成二进制决策,并且调整此阈值可使人们在假阳性和假阴性之间选择适当的折衷方案。
4.评估
首先,我们讨论用于量化结果的评估指标。然后,我们概述了实验设置,并讨论了生成真实数据的问题。结果在第5节中给出。
4.1 评估指标
接收器工作特性(ROC)和召回精度都是文献中流行的指标,有时可以互换使用。两者都抓住了一个事实,即我们希望增加正确的正数,同时最大程度地减少错误的正数。但是,对于特定的情况,指标之间的细微差异应该决定一个指标的选择。正如在[2]中观察到的那样,前一种方法非常适合评估分类器,因为错误检测率已得到很好的定义。后者更适合评估检测器,因为即使无法确定负数的总数,也可以通过1-精度正确表示相对于检测总数的错误检测数。
根据[14],我们选择在关键点匹配问题上测量SIFT局部描述符表示的性能,定义如下:给定一幅图像中的一个兴趣点,然后在数据集中找到该兴趣点的所有匹配项。显然,这是检测而不是分类任务(否定总数不明确),因此适当的度量标准是查全率。因此,尽管[14]使用ROC曲线,但本文还是介绍了召回率与1-精度图。
这些图如下生成。确定数据集中所有图像的关键点(使用SIFT算法的初始阶段)。检查来自不同图像的所有成对的关键点。如果特定关键点对的特征向量之间的欧式距离落在所选阈值以下,则该对称为匹配。正确-正匹配是两个关键点对应于相同物理位置的匹配(由标记图像的地面真实性确定,或者对合成图像变形测试使用已知的图像变换确定)。假阳性是两个关键点来自不同物理位置的匹配。给定数据集的阳性总数是先验的。从这些数字,我们可以确定召回率和1-精度:

召回=正确的阳性数/阳性的总数,1-精度=错误的阳性数/匹配总数(正确或错误)。
通过更改每种算法的阈值,我们为实验生成了查全率与1-精度图。
4.2 实验装置
我们进行了三种主要的实验类型,以探索标准SIFT表示法与PCA-SIFT之间的差异。第一种类型检查了每个描述符对(合成产生的)因噪声增加,照明变化和图像变换的应用而产生的影响的鲁棒性。我们收集了一个图像数据集2,并对每个图像进行了以下变换:(1)高斯噪声(σ= 0.05),其中图像强度在0到1之间; (2)旋转45度,然后缩放50%; (3)强度比例缩放为50%; (4)投影翘曲等效于大约30°的视角变化。
2可从以下网站获得:http://www.cs.cmu.edu/~yke/pcasift/
在这些实验中评估了三个描述符:(1)标准SIFT特征表示(表示为“ SIFT”); (2)第3节所述的PCA-SIFT(n = 20),其中本征空间对局部梯度进行建模(表示为“ Grad PCA 20”); (3)PCA-SIFT的一种变体,其中本征空间直接模拟局部图像补丁而不是局部梯度(表示为“ Img PCA 20”)。对于(3),我们采用标准强度归一化技术减去均值并按比例缩放至单位方差;没有此步骤,(3)的结果将更糟。
第二类评估从不同角度拍摄的真实图像上的两个描述符,例如INRIA MOVI Graffiti数据集[1]。第三类涉及将SIFT和PCA-SIFT集成到图像检索应用程序中。第6节中提供了其他实验来研究关键点定位误差,PCA组件的数量以及距离度量的选择。
4.3 生成真实数据
我们在每个图像上运行SIFT的初始阶段,以识别关键点。目标是为每对图像获取正确关键点匹配的列表。由于SIFT算法每个图像生成数百或数千个关键点,因此手动识别大型数据集的匹配将非常耗时且容易出错。幸运的是,了解两个图像之间的映射使我们能够自动解决匹配问题。对于涉及合成生成的目标图像的实验,这些图像变换是先验的。对于涉及Graffiti数据集的实验,给出了两个匹配场景之间的变换(表示为单应性)。我们使用该信息如下。
5.结果
本节介绍将PCA-SIFT与标准SIFT表示法在受控实验,Graftiti数据集和图像检索任务上进行比较的结果。
5.1 受控转换
图1给出了第一组匹配实验的结果,其中图像在受控条件下失真。

图1:匹配任务中的SIFT与PCA-SIFT,在受控条件下图像变形或损坏。 (a)目标图像被高斯噪声(强度范围的σ= 0.05)破坏。 (b)将目标图像旋转45°并缩放50%。 (c)将目标图像投影扭曲以模拟30°的视点变化。 (d)目标图像强度缩放了50%。 请注意,Recall轴从0.9开始,因为所有方法在此任务上的表现都非常好。
图1a显示,对于几乎所有精度值,PCA-SIFT都在处理噪声图像方面显着更好,并且PCA-SIFT(在梯度图上)主导了本地图像补丁的PCA表示。仅当可以容忍极高的误报率时,标准SIFT表示才优于PCA-SIFT。这些结果并不特别令人惊讶,因为PCA应该在高斯噪声的影响下提供出色的重建效果。我们的下一个实验研究了几何变换的影响。
图1b绘制了实验结果,其中目标图像旋转了45°,缩放比例为50%,而图1c显示了目标通过对应于30°面外旋转的透视变换使目标变形后的匹配。虽然没有一种表示特别适合此任务,但PCA-SIFT显然主导了其他两种算法。
图1d显示,所有表示都非常适合捕获照明的简单变化(请注意,召回轴已放大并偏移以突出显示差异)。仔细观察,我们可以看到在大多数领域中,标准SIFT表示都比PCA-SIFT稍好。但是,考虑到所有算法的召回率均超过95%,这并不是很重要。
5.2 INRIA Graffiti数据集
INRIA Graffiti [1]数据集包含从不同摄影机角度拍摄的覆盖墙壁的图像。由于场景是平面的,因此可以将图像之间的转换建模为二维平面单应性(在数据集中提供)。我们的目标是匹配图像之间的相应关键点。图2显示了Graffiti 6数据集上两种算法的匹配性能。尽管由于高度的投影变形,绝对召回率很低,但PCA-SIFT显然占主导地位。请注意,对于实际应用而言,高精度的低召回率是可以接受的。例如,PCA-SIFT在的精度为20%时,召回率约为5%。我们在图片中找到了大约一千个关键点,其中有50个是可靠的匹配项。对于诸如图像检索之类的应用,足够数量的可靠匹配是足够的。
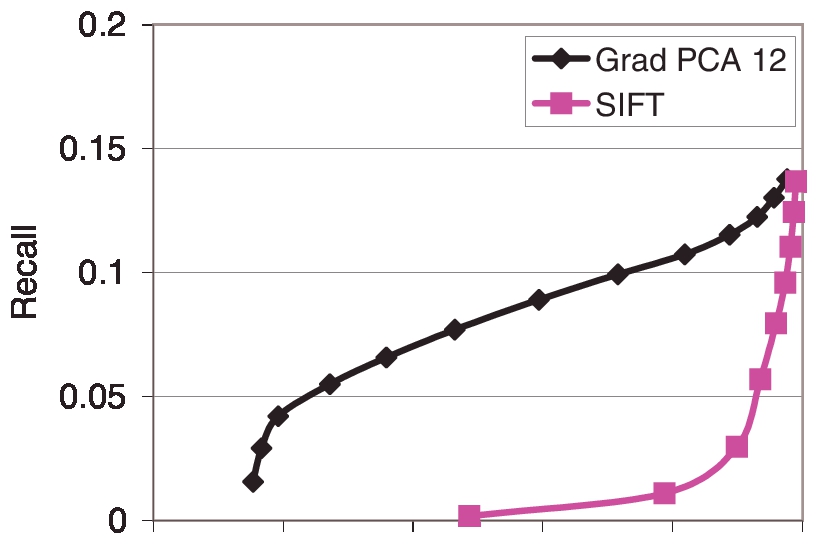
图2:在Graffiti 6 [1]上的SIFT与PCA-SIFT(n = 12)。
5.3 图像检索应用
我们已将SIFT和PCA-SIFT集成到用于从不同角度拍摄的真实场景的图像检索应用程序中。 与Graffiti数据集不同,场景不是平面的,包含遮挡和反射曲面。 使用SIFT进行图像检索的公式如下。 给定两个图像,我们首先提取它们对应的特征向量。 对于一幅图像中的每个特征向量,我们将其与另一幅图像中的所有特征向量进行比较,并对阈值距离内的特征数进行计数。 我们将匹配数视为图像之间的相似性。
在本实验中,我们选择了一个包含30张图像的小型数据集3(10个常见的家用物品,从不同的角度拍摄)。每个图像都用作对数据库的查询(以留一法的方式)。如果相应对象的其他两个图像都返回前三个位置,则该算法将获得2分;否则,该算法将获得2分。如果只有正确的比赛之一出现在前三名,则获得1分;否则,将不会获得任何积分。分数除以60(正确匹配的总数),并在表14中给出。每种算法的阈值距离已调整为可获得最佳结果(SIFT阈值:141; PCA-SIFT阈值:2200);实际上,各种各样的阈值都能很好地起作用。结果表明,PCA-SIFT在关键点上的匹配精度也可以转化为更好的检索结果。
3可从http://www.cs.cmu.edu/~yke/pcasift/获得。
4这等效于测量P(2),即检索两个对象时系统的精度。

表1:在我们的图像检索应用程序中正确检索的图像百分比。 PCA-SIFT的匹配精度可转化为重大的实际收益。

图3:在从不同角度拍摄的一些具有挑战性的真实世界图像上,SIFT和PCA-SIFT(n = 20)之间的比较。 (A)是一张杂乱的茶几的照片; (B)是INRIA Graffiti数据集中Graffiti覆盖的墙。 每个算法显示前十个匹配项:白色实线表示正确的匹配,而黑色虚线表示不正确的匹配。
图3显示了将SIFT应用于两个具有挑战性的场景(凌乱的茶几和Graffiti图像)的结果。我们手动设置阈值,以使每个算法返回10个匹配项。在这些实验中,PCA-SIFT显然主导了标准表示。特别是,后者似乎被几个对象的边缘弄糊涂了。
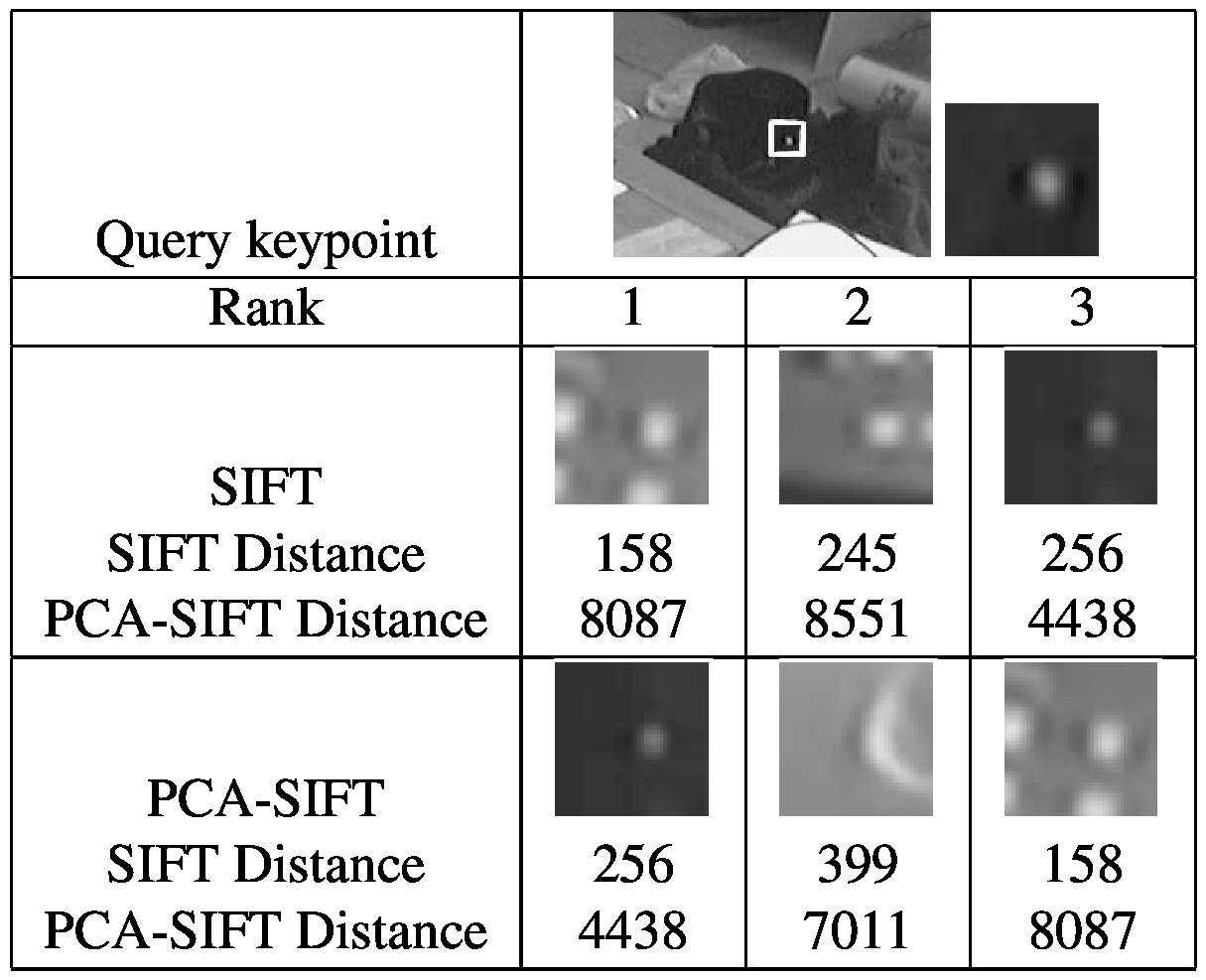
图4:仔细查看特定关键点的匹配结果(放大图3中的区域)。 显示了该关键点对于SIFT和PCA-SIFT的前三个匹配项(n = 20)。 正确的匹配在标准表示形式的列表中排在第三位,而它是PCA-SIFT的最高匹配。 两种算法使用不同的特征空间,因此距离值的直接比较没有意义。
图4详细显示了此示例中的关键点之一。对于每种算法,按等级顺序显示潜在的匹配项。当PCA-SIFT正确地将其排在第一位时,标准表示法将正确的匹配率评定为第三位。
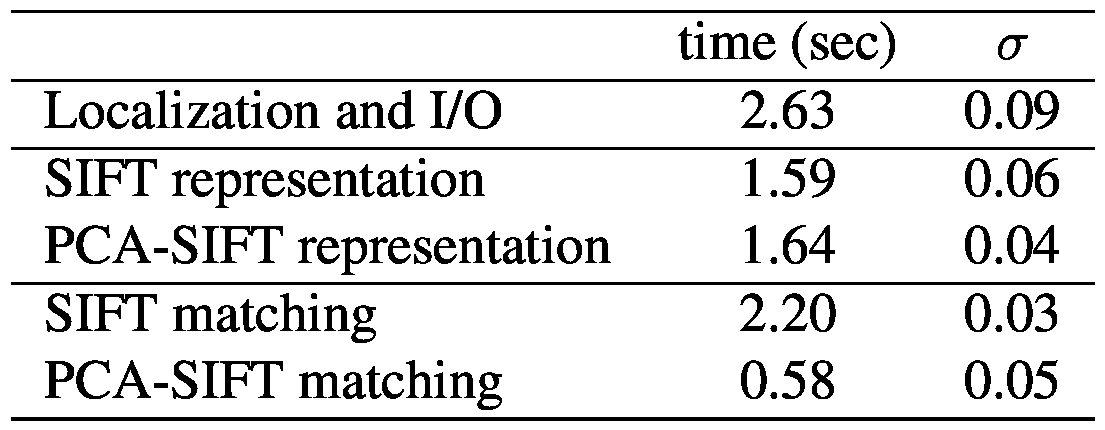
表2:在10次独立运行中,SIFT和PCA-SIFT(n = 20)的运行时间(和标准偏差)平均。 本地化和I / O步骤是两种算法共有的。 建立这两种表示需要花费相当的时间,但是使用PCA-SIFT进行匹配要快得多。
表2比较了SIFT和PCA-SIFT之间的运行时间。顶部显示了大约2200个兴趣点的图像特征提取。第一行是定位兴趣点所需的时间(两种算法均如此)。第二和第三行显示了计算描述符表示所需的时间。我们注意到计算表示所需的时间是可比的。该表的下部显示了PCA-SIFT在匹配阶段的速度显着提高。 PCA-SIFT(n = 20)仅需要三分之一的时间即可完成240万点的比较。
6.讨论
第5节表明,与标准SIFT本地描述符相比,PCA-SIFT既准确得多,又快得多。 但是,这些结果有些令人惊讶,因为后者是经过精心设计的,而PCA-SIFT是一个显而易见的想法。 现在,我们仔细研究该算法,并提出一些假设,这些假设可能有助于解释PCA-SIFT的成功。
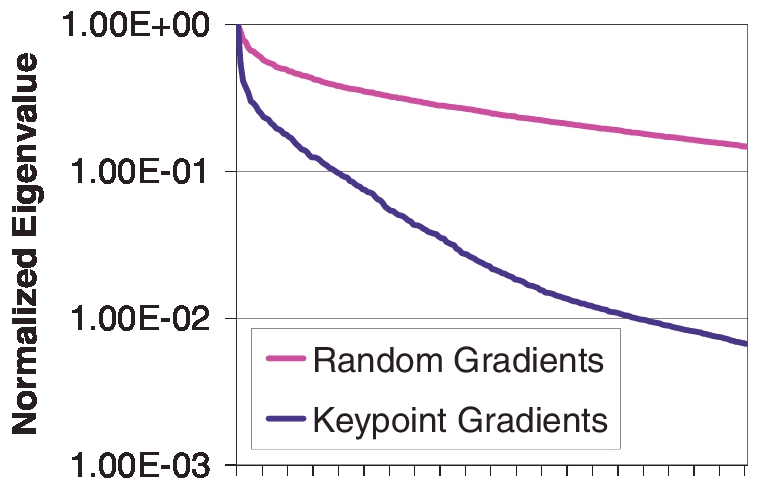
图5:此图显示,随机选择的梯度图像补丁上的PCA与PCA-SIFT不同,后者将PCA应用于围绕SIFT关键点的梯度补丁上。 PCA-SIFT的特征值衰减得更快得多,这支持了我们的信念,即PCA-SIFT使用少量尺寸即可成功表示关键点,因为仅需要PCA即可捕获非常特殊类型的图像补丁的外观。
图5显示,围绕SIFT关键点的渐变色块具有高度结构化,因此更易于使用PCA表示。 我们看到,这些色块的特征值衰减比随机选择的梯度色块的特征值衰减快得多。 这是因为,围绕关键点的面片均具有某些特征(源自SIFT关键点检测阶段):它们均以比例空间中的局部最大值为中心,旋转以将主要梯度与垂直方向对齐,并进行适当缩放。 这简化了PCA必须完成的工作,并使PCA-SIFT使用少量尺寸即可准确地表示补丁。
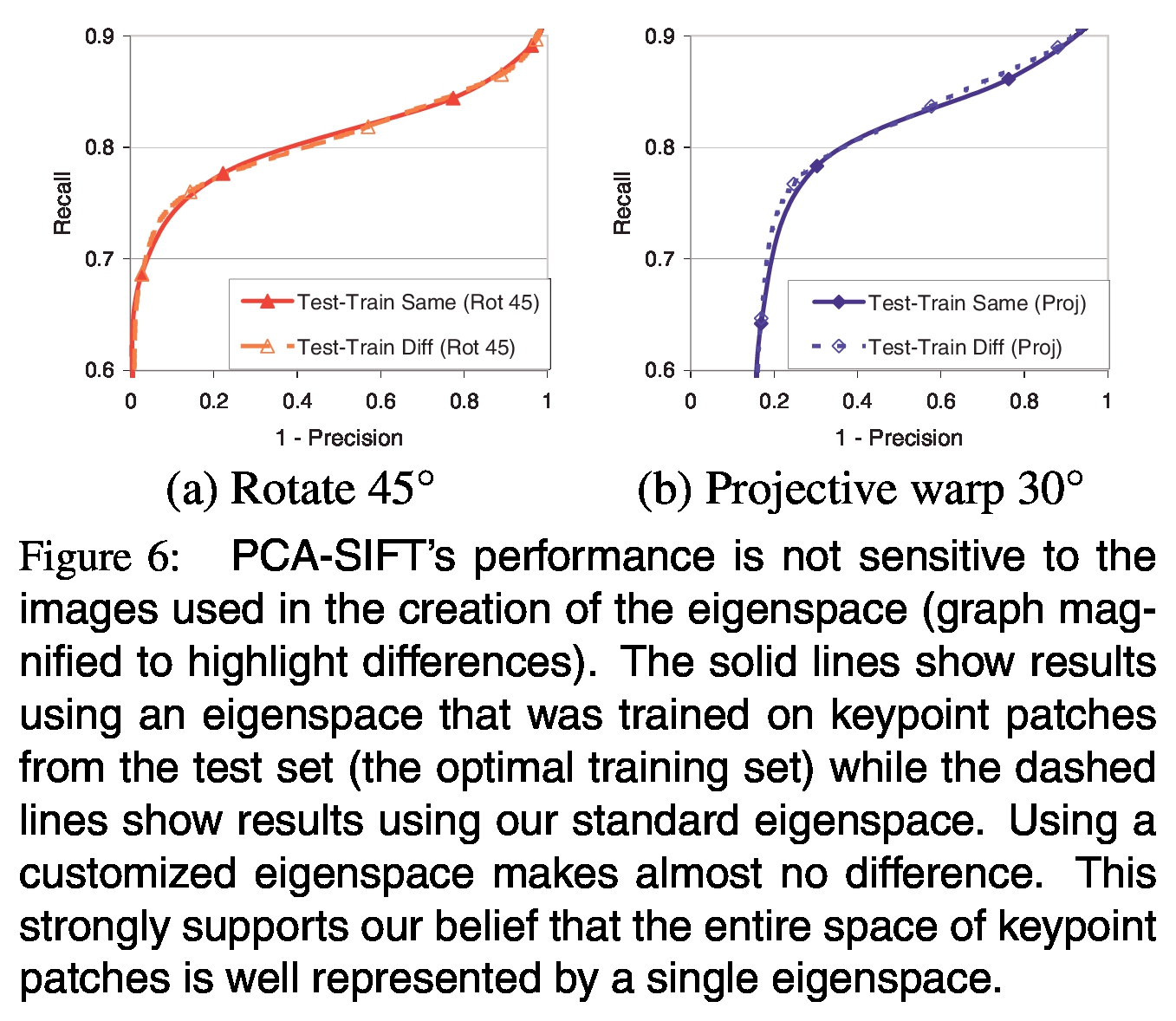
图6:PCA-SIFT的性能对本征空间创建过程中使用的图像不敏感(放大图以突出显示差异)。 实线表示使用特征空间对结果进行训练的结果,该特征空间是对来自测试集(最佳训练集)的关键点补丁进行训练的,而虚线示出了使用我们的标准特征空间进行的结果。 使用定制的本征空间几乎没有区别。 这有力地支持了我们的信念,即关键点补丁的整个空间都可以由单个特征空间很好地表示。
需要考虑的自然问题是,PCA-SIFT的表示是否对本征空间创建中使用的图像敏感-即,假设一个典型的本征空间来表示关键点梯度斑块是否合理?我们的实验表明,从不同图像集获得的关键点补丁生成的本征空间非常一致,而且PCA-SIFT的性能不需要我们专门为测试图像训练本征空间。图6显示了使用两个不同的特征空间执行的两个受控转换实验(在4.2节中进行了描述)的结果。在第一个实验中,目标图像旋转了45°;第二,目标图像被投影扭曲。第一个本征空间是针对此测试中使用的图像专门定制的。第二个本征空间是在一组不相关的图像上训练的(这是我们所有实验中使用的本征空间)。在每个实验中,PCA-SIFT在任一本征空间上的性能几乎相同;差异太小,无法在非比例尺图中看到,因此我们需要放大图6来突出显示它们。
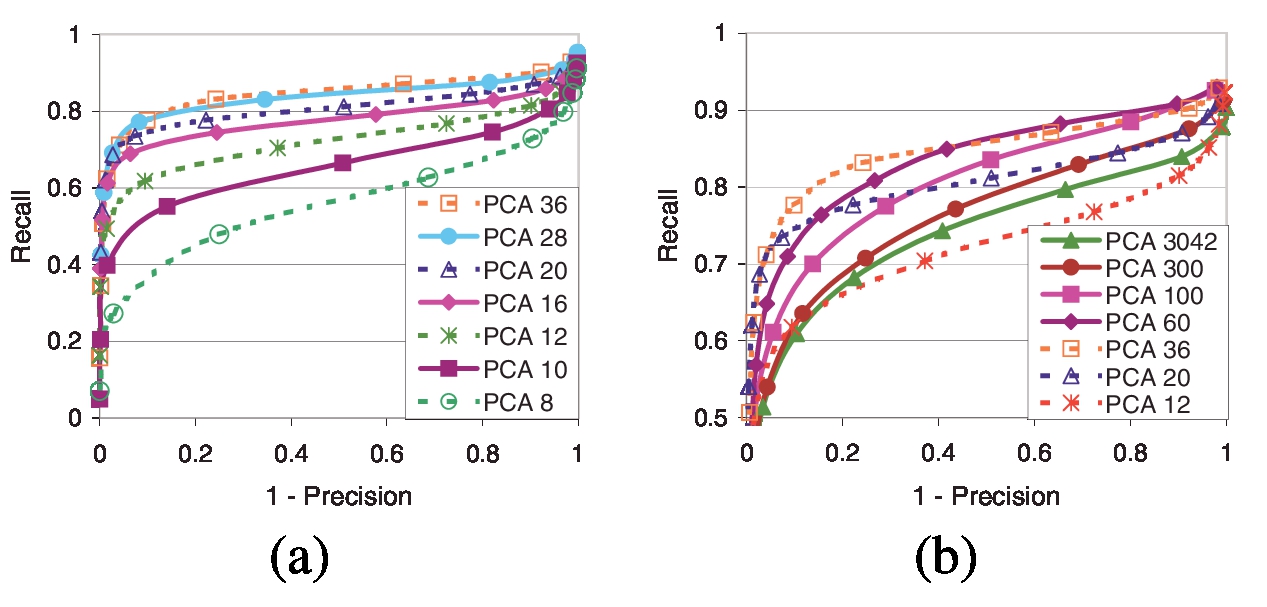
图7:随着PCA尺寸(n)的变化,PCA-SIFT性能。 n = 36可获得最佳匹配性能。
图7a显示了PCA-SIFT的匹配精度与特征空间的维数(对于n的较小值)之间的关系。如预期的那样,增加特征向量的维数会导致更好的精度,因为该表示法能够以更好的保真度捕获梯度补丁的结构。随着我们继续向特征向量添加维度,边际收益变慢。图7b显示了相同的图,其中n的值更大,因为表示中的维数接近输入矢量的维数。现在我们看到一个有趣的现象:一旦n超过某个大小,该算法的匹配精度实际上开始下降。在n = 3042处,PCA对输入向量执行完美(无损)重构,匹配精度仅略好于n = 12。我们的假设是,PCA子空间的第一个组件足以编码因关键点的身份(我们希望准确建模)而导致的梯度补丁中的变化,而后面的组件则代表了梯度中的细节无效或可能有害的图像,例如投影翘曲产生的扭曲。在运行时间和特征向量的维数之间也需要权衡。使用更少的组件需要更少的存储空间,并可以更快地进行匹配。我们在n = 20时获得了良好的结果。
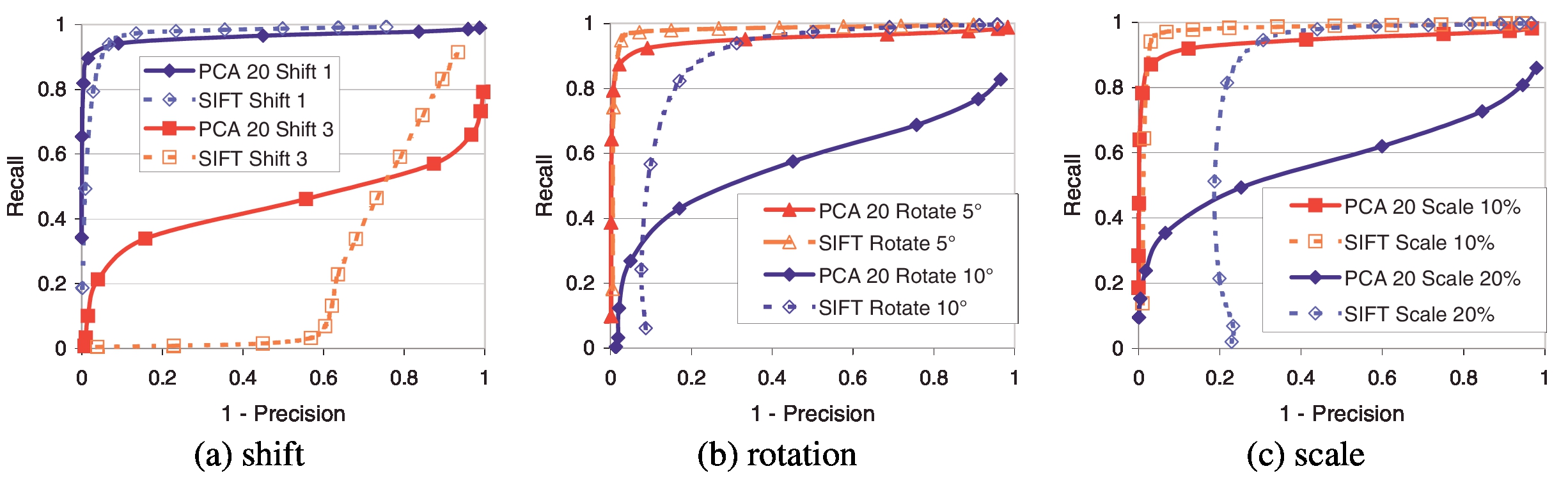
图8:在特征定位阶段直接引入附加误差时,SIFT与PCA-SIFT的关系(n = 20)。 SIFT本地化阶段给出的估算值偏移了kσ像素(k = 1、3;σ是提取特征的比例)。 经常观察到PCA对注册错误敏感; 但是,PCA-SIFT在这些条件下的性能非常好。 当旋转误差(5°和10°)或比例尺(10%和20%)破坏了定位时,SIFT的性能将超出PCA-SIFT,这是因为SIFT经过专门设计可抵抗检测器误差。
SIFT取得成功的原因之一是它的功能表示经过精心设计,可以抵抗定位错误。相反,众所周知,PCA对注册错误非常敏感。图8a显示了一个实验,其中我们在定位阶段之后引入了配准错误。相对于主导方向,我们在随机方向上添加了1和3个像素误差(以适当的比例)。令人惊讶的是,PCA-SIFT继续表现良好。但是,当在方向分配阶段(图8b)或比例尺估计(图8c)引入误差时,我们看到PCA-SIFT的准确性开始下降。这证实了我们的信念,即标准SIFT表示形式更适合处理这些错误。然而,我们的实验表明,SIFT算法的特征定位阶段在集中,定向和缩放关键点补丁方面非常出色。因此,在实践中很少(如果曾经)观察到标准SIFT表示法的这些好处。
我们假设PCA-SIFT的匹配精度可以归因于几个因素。 首先,在关键点附近使用渐变色块而不是原始色块可使表示对照明变化具有鲁棒性,并减少PCA需要建模的变化。 第二,SIFT的前三个阶段执行的预处理简化了PCA的建模问题,因为其余的变化是由于关键点标识和透视图失真而引起的。 第三,丢弃PCA中的较低组件可以消除由于未建模的失真引起的变化,从而提高了准确性。 最后,使用少量尺寸可在存储空间和匹配速度方面带来明显的好处。
7.结论
本文介绍了SIFT算法的局部图像描述符的替代表示形式。与标准表示相比,PCA-SIFT既更独特又更紧凑,从而显着提高了受控条件和实际条件下的匹配精度(和速度)。我们认为,尽管PCA不适合表示图像补丁的一般类别,但它非常适合捕获已在比例,空间和方向上定位的关键点的梯度图像中的变化。我们目前正在将表示形式扩展到彩色图像,并探索将PCA-SIFT背后的思想应用于其他关键点算法的方法。
8.致谢
Yan Ke受Intel Research Scholar计划的支持。感谢David Lowe提供的SIFT源代码和有关此主题的有用建议。也感谢拉里·休斯顿,菲尔·吉本斯和M. Satyanarayanan的宝贵反馈。
参考文献
[1] Viewpoint change sequences. http://www.inrialpes.fr/movi/.
[2] S. Agarwal and D. Roth. Learning a sparse representation for object detection. In Proceedings of European Conference on Computer Vision, pages 113–130, 2002.
[3] R. Fergus, P. Perona, and A. Zisserman. Object class recognition by unsupervised scale-invariant learning. In Proceedings of Computer Vision and Pattern Recognition, June 2003.
[4] W. T. Freeman and E. H. Adelson. The design and use of steerable filters. IEEE Trans. Pattern Analysis and Machine Intelligence, 13(9):891–906, 1991.
[5] K. Fukunaga and W. Koontz. Application of the Karhunen-Loeve expansion to feature selection and ordering. IEEE Trans. Communications, 19(4), 1970.
[6] C. Harris and M. Stephens. A combined corner and edge detector. In Alvey Vision Conference, pages 147–151, 1988.
[7] I. T. Joliffe. Principal Component Analysis. Springer-Verlag, 1986.
[8] J. Karhunen and J. Joutsensalo. Generalization of principal component analysis, optimization problems and neural networks. Neural Networks, 8(4), 1995.
[9] J. Koenderink and A. van Doorn. Representation of local geometry in the visual system. In Biological Cybernetics, volume 55, pages 367–375, 1987.
[10] D. Lee and S. Seung. Learning the parts of objects by non-negative matrix factorization. Nature, 401, 1999.
[11] D. G. Lowe. Object recognition from local scale-invariant features. In Proceedings of International Conference on Computer Vision, pages 1150–1157, 1999.
[12] D. G. Lowe. Distinctive image features from scale-invariant keypoints. International Journal of Computer Vision, 2004.
[13] K. Mikolajczyk and C. Schmid. Indexing based on scale invariant interest points. In Proceedings of International Conference on Computer Vision, pages 525–531, July 2001.
[14] K. Mikolajczyk and C. Schmid. A performance evaluation of local descriptors. In Proceedings of Computer Vision and Pattern Recognition, June 2003.
[15] H. Murase and S. Nayar. Detection of 3D objects in cluttered scenes using hierarchical eigenspace. Pattern Recognition Letters, 18(4), April 1997.
[16] F. Schaffalitzky and A. Zisserman. Multi-view matching for unordered image sets. In Proceedings of European Conference on Computer Vision, volume 1, pages 414–431. Springer-Verlag, 2002.
[17] M. Turk and A. Pentland. Face recognition using eigenfaces. In Proceedings of Computer Vision and Pattern Recognition, 1991.
[18] L. Van Gool, T. Moons, and D. Ungureanu. Affine/photometric invariants for planar intensity patterns. In Proceedings of European Conference on Computer Vision, 1996.
posted on 2019-10-03 13:22 Alliswell_WP 阅读(428) 评论(0) 收藏 举报

 浙公网安备 33010602011771号
浙公网安备 33010602011771号