Computer Vision_33_SIFT：Object recognition from local scale-invariant features——1999

此部分是计算机视觉部分，主要侧重在底层特征提取，视频分析，跟踪，目标检测和识别方面等方面。对于自己不太熟悉的领域比如摄像机标定和立体视觉，仅仅列出上google上引用次数比较多的文献。有一些刚刚出版的文章，个人非常喜欢，也列出来了。

33. SIFT
关于SIFT，实在不需要介绍太多，一万多次的引用已经说明问题了。SURF和PCA-SIFT也是属于这个系列。后面列出了几篇跟SIFT有关的问题。
[1999 ICCV] Object recognition from local scale-invariant features
[2000 IJCV] Evaluation of Interest Point Detectors
[2006 CVIU] Speeded-Up Robust Features (SURF)
[2004 CVPR] PCA-SIFT A More Distinctive Representation for Local Image Descriptors
[2004 IJCV] Distinctive Image Features from Scale-Invariant Keypoints
[2010 IJCV] Improving Bag-of-Features for Large Scale Image Search
[2011 PAMI] SIFTflow Dense Correspondence across Scenes and its Applications

 

翻译

从局部尺度不变特征识别物体——http://tongtianta.site/paper/56806

作者：David G. Lowe

 

摘要 -已经开发了使用新型本地图像特征的对象识别系统。这些特征对于图像缩放，平移和旋转是不变的，而对于照明变化和仿射或3D投影则是部分不变的。这些功能与下颞叶皮质的神经元具有相似的属性，这些属性用于灵长类动物视觉中的物体识别。通过分阶段筛选方法可以有效地检测特征，该方法可以识别比例尺空间中的稳定点。通过在多个方向平面和多个比例上表示模糊的图像梯度，创建允许局部几何变形的图像关键点。这些键用作识别候选对象匹配项的最近邻居索引方法的输入。通过为未知模型参数找到一个低残差最小二乘解，可以完成对每个匹配项的最终验证。实验结果表明，在杂乱的部分遮挡图像中，可以以不到2秒的计算时间实现鲁棒的目标识别。

 

1 简介

在杂乱的现实场景中进行对象识别需要不受附近杂乱或部分遮挡影响的局部图像特征。这些特征必须至少部分不变于照明，3D投影变换和常见对象变化。另一方面，这些特征还必须具有足够的独特性，以在许多替代方案中标识特定的对象。对象识别问题的困难在很大程度上是由于未能成功找到这种图像特征。但是，最近对密集局部特征的使用的研究(例如，Schmid＆Mohr [19])表明，通常可以通过使用在大量可重复位置采样的局部图像描述符来实现有效的识别。

本文提出了一种新的图像特征生成方法，称为尺度不变特征变换(SIFT)。这种方法将图像转换成大量的局部特征向量，每个局部特征向量对于图像的平移，缩放和旋转都是不变的，而对于照明变化和仿射或3D投影则是部分不变的。先前的局部特征生成方法缺乏尺度不变性，并且对投影失真和照明变化更敏感。SIFT功能与灵长类动物视力下颞叶(IT)皮质中神经元的反应具有许多共同的特性。本文还描述了索引和模型验证的改进方法。

通过使用分级过滤方法，可以有效地识别尺度不变特征。第一阶段通过寻找高斯差函数的最大值或最小值的位置来确定尺度空间中的关键位置。每个点都用于生成特征向量，该特征向量描述相对于其比例空间坐标系采样的局部图像区域。通过模糊图像梯度位置，这些功能实现了局部变化的局部不变性，例如仿射或3D投影。该方法基于哺乳动物视觉的大脑皮层中复杂细胞行为的模型。所得的特征向量称为SIFT键。在当前的实现中，每个图像生成1000个SIFT键的数量级，此过程需要少于1秒的计算时间。

从图像派生的SIFT密钥在最近邻方法中用于索引以标识候选对象模型。首先通过霍夫变换哈希表，然后通过最小二乘法拟合最终确定模型参数，来确定与潜在模型姿势一致的键集合。当至少三个键在残差低的模型参数上达成一致时，有充分的证据表明存在物体。由于典型对象的图像中可能有数十个SIFT键，因此可能在图像中具有大量的遮挡，但仍保持较高的可靠性。

当前的对象模型表示为SIFT密钥的2D位置，可以进行仿射。在特征位置上进行足够的变化可以识别平面形状的透视投影，该平面投影距离相机最多60度旋转，或者允许3D对象最多20度旋转。

2.相关研究

对象识别已在机器视觉行业中广泛用于检查，注册和操纵的目的。但是，当前用于对象识别的商业系统几乎完全依赖于基于相关性的模板匹配。虽然对于严格控制对象姿态和照明的某些工程环境非常有效，但是当允许对象旋转，缩放，照明和3D姿态发生变化时，模板匹配在计算上就变得不可行，在处理部分可见性和大型模型时甚至更是如此数据库。

在所有图像位置搜索匹配项的一种替代方法是从图像中提取至少部分不变于图像形成过程并仅与那些特征匹配的特征。已经提出并探索了许多候选特征类型，包括线段[6]，边缘分组[11、14]和区域[2]，还有许多其他提议。尽管这些功能对于某些对象类别效果很好，但常常检测不到的频率不够频繁或稳定性不足，无法为可靠识别奠定基础。

最近开发了密度更高的图像特征集合。一种方法是使用拐角检测器(更准确地说，是局部图像变化中的峰值的检测器)来标识可重复的图像位置，在该位置附近可以测量局部图像属性。张等。 [23]使用哈里斯角检测器来识别特征位置，以对从不同视点拍摄的图像进行极线对准。与其尝试使一幅图像的区域与第二幅图像中的所有可能区域相关联，不如通过仅匹配以每幅图像中的拐角点为中心的区域来节省大量的计算时间。

对于物体识别问题，Schmid＆Mohr [19]也使用哈里斯角检测器来识别兴趣点，然后根据高斯导数图像测量的方向不变矢量在每个兴趣点上创建一个局部图像描述符。 这些图像描述符通过寻找满足基于对象的方向和位置约束的多个匹配描述符，用于鲁棒的对象识别。 这项工作对于大型数据库中的识别速度以及处理混乱图像的能力都给人留下了深刻的印象。

这些先前方法中使用的拐角检测器有一个主要缺陷，那就是它们仅以单一比例检查图像。随着比例尺的变化变得明显，这些检测器会响应不同的图像点。另外，由于检测器未提供物体比例的指示，因此有必要创建图像描述符并尝试以大量比例进行匹配。本文介绍了一种有效的方法来确定尺度空间中的稳定关键位置。这意味着图像的不同缩放比例不会影响所选的关键位置集。此外，为每个点确定一个显式比例，这允许在每个图像中以等效比例对那个点的图像描述矢量进行采样。在每个位置确定规范的方向，以便可以相对于一致的局部2D坐标系执行匹配。与Schmid和Mohr使用的旋转不变的图像描述符相比，这允许使用更多与众不同的图像描述符，并且对描述符进行了进一步修改以提高其对仿射和照度变化的稳定性。

其他基于外观的识别方法包括特征空间匹配[13]，颜色直方图[20]和接受域直方图[18]。这些方法都已经在孤立的物体或预先分割的图像上得到了成功的证明，但是由于它们具有更全面的功能，很难将它们扩展到混乱且部分遮挡的图像上。Ohba＆Ikeuchi [15]通过使用许多小的局部本征窗口成功地将本征空间方法应用于杂乱的图像，但这需要昂贵的搜索新图像中的每个窗口，如模板匹配。

3.关键点定位

我们希望确定图像缩放空间中相对于图像平移，缩放和旋转不变的位置，并且这些位置受噪声和小失真的影响最小。Lindeberg [8]表明，在尺度不变性的一些相当普遍的假设下，高斯核及其导数是用于尺度空间分析的唯一可能的平滑核。

 

为了实现旋转不变性和高效率，我们选择了在比例空间中应用的高斯函数差的最大值和最小值处选择关键位置。通过建立一个图像金字塔并在每个级别之间进行重采样，可以非常有效地计算出该图像。此外，它将关键点定位在变化较大的区域和尺度上，从而使这些位置对于表征图像特别稳定。Crowley＆Parker [4]和Lindeberg [9]以前曾将标高空间中的高斯差用于其他目的。在下文中，我们描述了一种特别有效且稳定的方法来检测和表征此函数的最大值和最小值。

由于2D高斯函数是可分离的，因此可以通过在水平和垂直方向上应用1D高斯函数的两次遍历来有效地计算其与输入图像的卷积：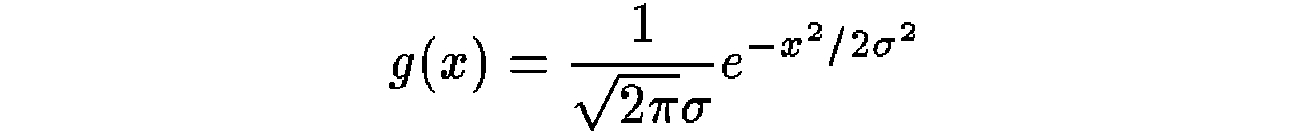

对于关键定位，所有的平滑操作都使用完成，可以使用带有7个采样点的1D内核以足够的精度对其进行近似。

 

首先使用将输入图像与高斯函数卷积得到图像A。然后，使用的进一步增量平滑第二次重复此操作，以提供一个新图像B，该图像现在具有σ=2的有效平滑。高斯函数的差是通过从A中减去图像B来获得的，从而得出两个高斯之间的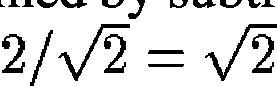之比。

为了生成下一个金字塔等级，我们使用双线性插值对每个方向上像素间距为1.5的已平滑图像B进行重新采样。尽管使用的相对比例进行重新采样似乎更自然，但唯一的限制是采样频率足够频繁以检测峰。1.5间距意味着每个新样本将是4个相邻像素的恒定线性组合。这对于计算和最小化因更改重采样系数而产生的混叠伪影非常有效。

 

通过将金字塔中的每个像素与其相邻像素进行比较，可以确定此比例空间函数的最大值和最小值。首先，将一个像素与其在金字塔相同级别的8个相邻像素进行比较。如果在此级别上是最大值或最小值，则考虑1.5倍的重采样，在金字塔的下一个最低级别上计算最近的像素位置。如果像素保持高于(或低于)该最接近的像素及其8个邻居，则对以上级别重复测试。由于大多数像素将在几次比较中消除，因此这种检测的成本很小，并且比建造金字塔的成本低得多。

果金字塔的第一层以与输入图像相同的速率采样，则最高空间频率将被忽略。这归因于初始平滑，这需要提供峰的分离以进行可靠的检测。因此，在构建金字塔之前，我们使用双线性插值将输入图像扩展2倍。对于典型的512*512像素图像，这大约可提供1000个关键点，而没有初始扩展的像素点只有四分之一。

3.1 SIFT关键点稳定性

为了表征每个关键位置的图像，对金字塔每个级别的平滑图像A进行处理，以提取图像梯度和方向。在每个像素A_ij处，使用像素差计算图像梯度量级M_ij和方向R_ij：

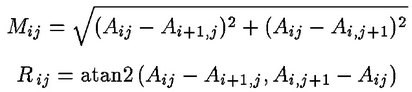
通过将梯度量级设置为最大可能梯度值的0.1倍来提高照明变化的鲁棒性。这会降低具有3D浮雕的表面的照明方向更改的影响，因为照明更改可能会导致梯度幅度发生较大变化，但可能对梯度方向的影响较小。

 

由于先前的平滑程度很高，因此像素差异可高效计算并提供足够的精度。 确定关键位置时，将补偿有效的半像素位置偏移。

通过将梯度幅度设置为最大可能梯度值的0.1倍，可以增强照明变化的鲁棒性。 这会降低具有3D浮雕的表面的照明方向更改的影响，因为照明更改可能会导致梯度幅度发生较大变化，但可能对梯度方向的影响较小。

为每个关键位置分配了规范的方向，以使图像描述符对于旋转不变。 为了使其在光照或对比度变化方面尽可能稳定，该方向由局部图像梯度方向直方图中的峰值确定。 使用高斯加权窗口创建方向直方图，该窗口的σ是当前平滑比例的3倍。 这些权重乘以阈值梯度值，并累积在直方图中对应于方向R_ij 的位置。 直方图有36个bin，覆盖了360度旋转范围，并在选择峰之前进行了平滑处理。

可以通过对自然图像进行适当的投影，对比度和亮度变化以及添加噪声来测试所得键的稳定性。根据变换参数的知识，可以在变换后的图像中预测在第一个图像中检测到的每个键的位置。该框架用于选择上面给出的各种采样和平滑参数，以便可以在保持变化稳定性的同时获得最大的效率。

图1显示了仅在较大音阶的2个八度音阶范围内检测到的按键数量相对较少(以避免过度混乱)。 每个键均显示为正方形，从中心到正方形一侧的线表示方向。 在此图的后半部分，图像在水平方向上旋转了15度，缩放了0.9倍，并拉伸了1.1倍。 像素强度在0到1的范围内，从其亮度值中减去0.1，并通过乘以0.9降低对比度。 然后添加随机像素噪声，以提供少于5位/像素的信号。 尽管进行了这些转换，但第一张图像中78％的关键点在预测位置，比例和方向上都与第二张图像中的关键点紧密匹配。

图1：第二张图像是通过旋转，缩放，拉伸，亮度和对比度的变化以及像素噪声的添加而产生的。尽管进行了这些更改，但第一张图像中78％的键在第二张图像中具有紧密匹配的键。这些示例仅显示了减少杂乱的按键子集。

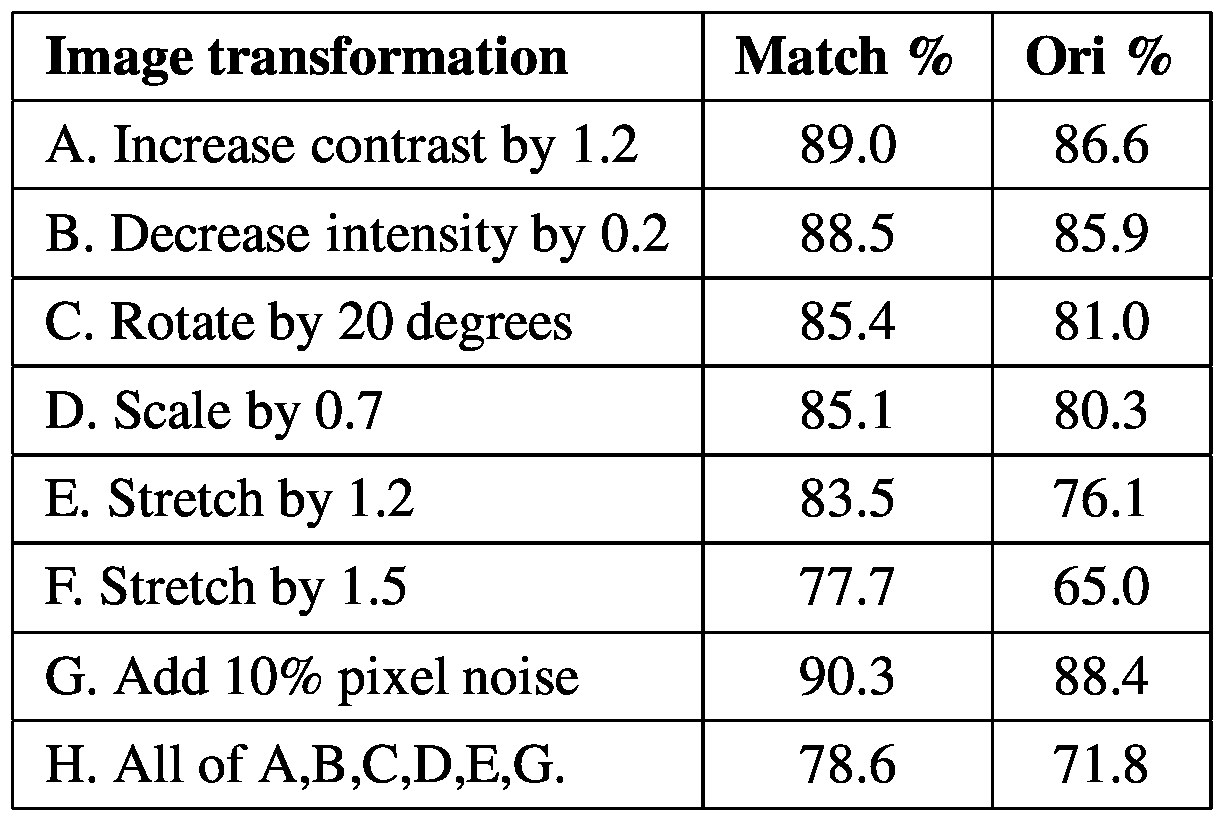
图2：对于应用于20个图像样本的各种图像变换，此表给出了在匹配位置和比例(匹配百分比)以及方向(Ori％)上匹配的关键帧的百分比。

4.本地图片描述

给定每个键的稳定位置，比例和方向，现在可以以不变于这些变换的方式描述局部图像区域。此外，还需要使这种表示方式对局部几何的小变化(例如由细微或3D投影引起的变化)具有鲁棒性。

视觉皮层中复杂神经元的响应特性提出了一种解决方案，其中在保持方向和空间频率特异性的同时，允许特征位置在较小区域内变化。Edelman，Intrator＆Poggio [5]进行了模拟复杂神经元对计算机图形模型的不同3D视图的响应的实验，发现与简单的基于相关的匹配相比，复杂的细胞输出提供了更好的辨别力。例如，如果一个假的投影在一个方向上相对于另一个方向拉伸了图像，这可以看到，这会改变渐变特征的相对位置，同时对其方向和空间频率的影响较小。

通过用表示多个取向(称为取向平面)中的每一个的多个图像来表示局部图像区域，可以获得对局部几何变形的鲁棒性。每个方向平面仅包含与该方向相对应的渐变，其中线性插值用于中间方向。每个方向平面都经过模糊处理并重新采样，以允许梯度位置发生较大变化。

通过为金字塔的每个级别使用与方向选择相同的预先计算的梯度和方向，可以有效地实现此方法。对于每个关键点，我们使用检测到关键点的金字塔等级的像素采样。围绕关键位置落入半径为8像素的半径的圆中的像素将插入到定向平面中。通过减去按键的方向来测量相对于按键的方向。对于我们的实验，我们使用了8个方向平面，每个方向平面都是在4*4位置网格上采样的，采样间隔是用于梯度检测的像素间距的4倍。通过使用方向和两个空间维度上的线性插值，通过在样本网格中的每个像素的8个最邻近像素之间分配每个像素的梯度来实现模糊。这种实现比执行显式模糊和重采样要有效得多，但几乎可以得到等效的结果。

为了以更大的比例对图像进行采样，对金字塔的第二个级别(高一个八度)重复相同的过程。但是，这次使用的是2*2而不是4*4示例区域。这意味着将在两个比例尺上检查大约相同的图像区域，以使任何附近的遮挡对一个比例尺的影响不会超过另一个比例尺。因此，两个尺度上的SIFT关键向量中的样本总数为8*4*4+8*2*2或160个元素，可提供足够的测量结果以实现高特异性。

 

5.索引和匹配

为了建立索引，我们需要存储样本图像的SIFT键，然后从新图像中识别匹配的键。如果需要精确的解决方案，则识别高维向量的最相似键的问题具有很高的复杂性。但是，对k-d树算法的一种改进(称为最佳bin-first搜索方法)(Beis＆Lowe [3])可以仅使用有限的计算量就可以高概率地识别最近的邻居。为了进一步提高最佳仓位优先算法的效率，在较大规模下生成的SIFT关键样本的权重是较小规模上的两倍。这意味着较大的比例实际上可以过滤最可能的邻居以较小的比例进行检查。通过将更多的权重分配给最低噪点范围，这也提高了识别性能。在我们的实验中，可能有一个极限值，可以在对30,000个关键向量进行的概率最佳优先搜索中检查多达200个邻居，而与寻找精确解决方案相比，几乎没有性能损失。

对可靠的模型假设进行聚类的一种有效方法是使用Hough变换[1]搜索符合特定模型姿势的键。数据库中的每个模型键都包含一个相对于模型坐标系的键参数记录。因此，我们可以在哈希表中创建一个条目，根据匹配假设预测模型的位置，方向和比例。我们使用30度的bin大小作为方向，比例使用2倍，并且将最大模型尺寸作为位置的0.25倍。这些相当宽的分箱大小甚至在由于3D视点变化而导致的实质几何变形的情况下也可以进行聚类。为了避免散列中的边界效应问题，每个假设被散列到每个维度中的2个最接近的bin中，每个假设总共提供16个哈希表条目。

6.适当参数的解决方案

搜索哈希表以识别一个箱中至少3个条目的所有群集，然后将这些箱按大小的降序排序。然后，对每个此类聚类进行验证过程，在该过程中，对将模型与图像相关的精细投影参数执行最小二乘解。

从模型点[x y]^T到图像点[u v]^T的相似转换可以写成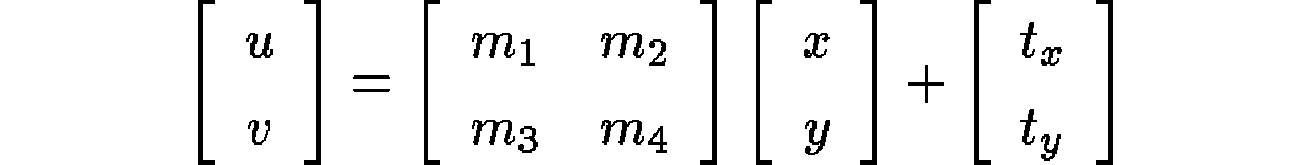

其中模型平移为[t_x t_y]^T，并且适当的旋转，缩放和拉伸由m_i参数表示。

我们希望求解变换参数，因此上面的等式可以重写为..

该方程式显示单个匹配项，但是可以添加任意数量的其他匹配项，每个匹配项在第一个和最后一个矩阵中贡献了另外两行。提供解决方案至少需要3个匹配项。

我们可以把这个线性系统写成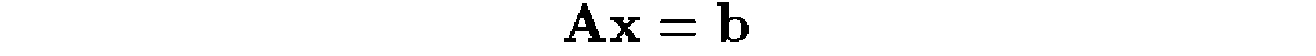

参数x的最小二乘解可以通过求解相应的正规方程来确定，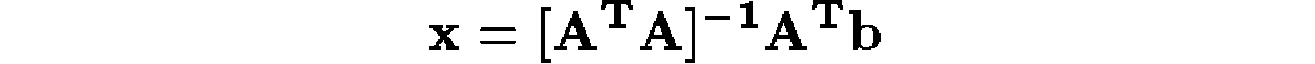

这样可以最大程度地减少从投影模型位置到相应图像位置的距离的平方和。这种最小二乘方法很容易扩展到求解关节和柔性物体的3D姿态和内部参数[12]。

给定参数解，现在可以通过检查每个图像特征与模型之间的一致性来删除异常值。每次比赛都必须在15度方向上达成一致，的比例会发生变化，并且位置上的最大模型大小应为0.2倍。如果在丢弃异常值后剩余少于3分，则比赛被拒绝。如果丢弃任何异常值，则将最小二乘解与其余点重新求解。

 

7.实验

相似的解决方案为平面对象的透视投影提供了很好的近似，因此平面模型为该方法提供了良好的初始测试。图3的第一行显示了对象矩形平面的三个模型图像。该图还显示了包含平面对象的杂乱图像，并且在识别后显示的同一图像覆盖了模型。显示的模型密钥是用于识别和最终最小二乘法的密钥。由于仅需要3个密钥即可进行可靠的识别，因此可以看出，这些解决方案具有很高的冗余度，并且可以在大量遮挡下幸存。还显示了使用最小二乘解的仿射变换投影的模型图像的矩形边界。除了透视投影引入的小误差外，这些与图像中平面区域的真实边界非常吻合。对于平面物体的许多图像已经进行了类似的实验，并且已经证明该识别对于在远离相机的任何方向上至少60度旋转物体具有鲁棒性。

图3：平面对象的模型图像显示在第一行。下面的识别结果显示了模型轮廓和用于匹配的图像键。

尽管模型图像和合适的参数不能说明3D对象深度的旋转，但它们仍然足以在每个模型视图深度大约20度旋转范围内对3D对象进行可靠的识别。图4的第一行显示了三个模型图像的示例。这些模型在黑色背景上拍摄，并通过分割背景区域来提取对象轮廓。在同一图中显示了一个识别示例，再次显示了用于识别的SIFT密钥。使用轮廓参数解决方案来投影对象轮廓，但是这次的一致性不是那么紧密，因为解决方案没有考虑深度旋转。图5显示了更多示例，其中存在明显的部分遮挡。

图4：第一行显示了3D对象的模型图像，并通过背景分割找到了轮廓。下图显示了3D对象的识别结果，其中包含模型轮廓和用于匹配的图像键。

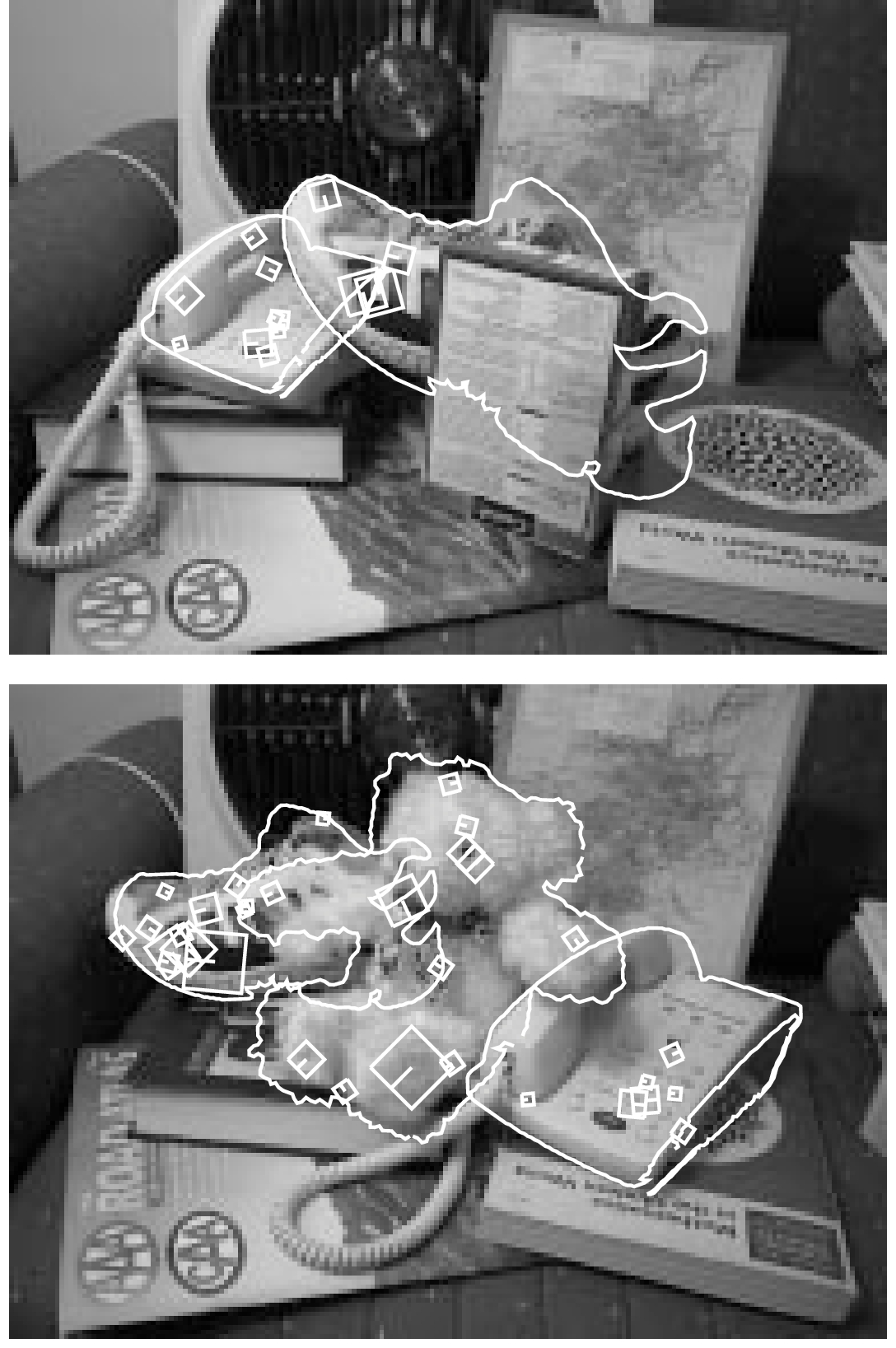
图5：遮挡的3D对象识别示例。

这些示例中的图像尺寸为384*512像素。在Sun Sparc 10处理器上，识别每个图像中所有对象的计算时间约为1.5秒，构建比例尺金字塔和识别SIFT键大约需要0.9秒，执行索引和最小二乘验证大约需要0.6秒。这不包括对每个模型图像进行预处理的时间，每个图像大约需要1秒钟，但是对于初始输入到模型数据库中只需要执行一次即可。

SIFT键的照度不变如图6所示。这两个图像从相同的视点具有相同的场景，除了第一个图像从左上角照亮，第二个图像从右中角照亮。运行完整识别系统以使用第一张图像作为模型来识别第二张图像，并且第二张图像被正确识别为与第一张图像匹配。仅显示识别中的SIFT键。作为最终匹配的一部分，已验证了273个键，这意味着在每种情况下，不仅在同一位置检测到相同的键，而且还与第二张图像中正确的对应键最接近。这些键中的任何三个都足以识别。虽然在高光或阴影发生变化的某些区域(例如，在相机的发光顶部)找不到匹配的键，但是这些键通常对照明变化表现出良好的不变性。

图6：在不同的照明条件下测试了图像按键的稳定性。第一个图像从左上角照亮，第二个从右中角照亮。底部图像中显示的键是用于将第二个图像与第一个图像进行匹配的键。

8.与生物视觉的联系

人类视觉的性能显然远远优于当前的计算机视觉系统，因此通过模拟生物过程可能会获得很多收益。幸运的是，在过去几年中，在了解如何在动物和人类中实现对象识别方面取得了巨大进步。

神经科学方面的最新研究表明，灵长类动物的目标识别利用了中等复杂度的特征，这些特征在规模，位置和照度的变化上基本不变(Tanaka [21]，Perrett＆Oram [16])。在下颞叶皮层(IT)中发现的这种中间特征的一些例子是对五角星状的深色作出反应的神经元，带有薄的突出元素的圆或三角形边界内的水平纹理区域。这些神经元对形状特征保持高度特定的响应，这些形状特征出现在视场的很大一部分内，并且范围在几个八度音阶范围内(Ito等人[7])。尽管也有一些神经元对更复杂的形状(例如脸部)做出反应，但许多这些特征的复杂性似乎与当前的SIFT特征大致相同。除了形状之外，许多神经元还对颜色和纹理属性做出反应。研究表明，特征响应取决于先前的视觉学习，即从接触包含特征的特定对象开始(Logothetis，Pauls和Poggio [10])。这些特征似乎是通过高度计算密集的并行过程在大脑中得出的，这与本文中给出的分阶段滤波方法完全不同。但是，结果几乎是相同的：将图像转换为一大组局部特征，每个局部特征都匹配一小部分潜在对象，但对于常见的观看变换却基本不变。

还众所周知，大脑中的对象识别取决于一系列注意过程，以将特征绑定到对象解释，确定姿势并从凌乱的背景中分割出对象[22]。据推测，该过程在验证中的作用与本文中使用的参数求解和离群值检测相同，因为解释的准确性通常取决于强制执行单个视点约束[11]。

9.结论和评论

SIFT功能在很大程度上不改变比例，照度和局部仿射畸变，从而比以前的方法有所改进。典型图像中的大量特征允许在杂波图像中的部分遮挡下进行稳健识别。与仅依赖索引的方法相比，可以解决最终模型参数的最终阶段可以进行更准确的验证和姿态确定。

进一步研究的重要领域是从代表对象3D结构的多个视图构建模型。这将具有进一步的优势，即可以将来自多个查看条件的键组合到一个模型中，从而增加了在新视图中查找匹配项的可能性。这些模型可以是基于运动结构的解决方案的真实3D表示，也可以根据自动聚类和插值来表示外观空间(Pope＆Lowe [17])。后一种方法的优点是它还可以对非刚性变形进行建模。

通过添加新的SIFT要素类型以合并颜色，纹理和边缘分组以及变化的要素尺寸和偏移，可以进一步提高识别性能。在背景杂乱可能会干扰其他特征的物体边界处，进行局部数字地面识别的比例不变边缘分组将特别有用。标引和验证框架允许将所有类型的比例尺和旋转不变特征合并到单个模型表示中。通过检测许多不同的特征类型并依靠索引和聚类来选择在特定图像中最有用的特征，可以实现最大的鲁棒性。

 

参考文献

[1] Ballard, D.H., “Generalizing the Hough transform to detect arbitrary patterns,” Pattern Recognition, 13, 2 (1981), pp.111-122.
[2] Basri, Ronen, and David.W. Jacobs, “Recognition using region correspondences,” International Journal of Computer Vision, 25, 2 (1996), pp. 141–162.
[3] Beis, Jeff, and David G. Lowe, “Shape indexing using approximate nearest-neighbour search in high-dimensional spaces,”Conference onComputerVision and PatternRecognition, Puerto Rico (1997), pp. 1000–1006.
[4] Crowley, James L., and Alice C. Parker, “A representation for shape based on peaks and ridges in the difference of lowpass transform,” IEEE Trans. on Pattern Analysis and Machine Intelligence, 6, 2 (1984), pp. 156–170.
[5] Edelman, Shimon, Nathan Intrator, and Tomaso Poggio,“Complex cells and object recognition,” Unpublished Manuscript, preprint at http://www.ai.mit.edu/~edelman/mirror/nips97.ps.Z
[6] Grimson, Eric, and Thom´as Lozano-P´erez, “Localizing overlapping parts by searching the interpretation tree,” IEEE Trans. on Pattern Analysis and Machine Intelligence, 9 (1987), pp. 469–482.
[7] Ito, Minami, Hiroshi Tamura, Ichiro Fujita, and Keiji Tanaka, “Size and position invariance of neuronal responses in monkey inferotemporal cortex,” Journal ofNeurophysiology, 73, 1 (1995), pp. 218–226.
[8] Lindeberg, Tony, “Scale-space theory: A basic tool for analysing structures at different scales”, Journal of Applied Statistics, 21, 2 (1994), pp. 224–270.
[9] Lindeberg, Tony, “Detecting salient blob-like image structures and their scales with a scale-space primal sketch: a method for focus-of-attention,” International Journal of Computer Vision, 11, 3 (1993), pp. 283–318.
[10] Logothetis,NikosK., Jon Pauls, andTomasoPoggio, “Shape representation in the inferior temporal cortex of monkeys,”Current Biology, 5, 5 (1995), pp. 552–563.
[11] Lowe, David G., “Three-dimensional object recognition from single two-dimensional images,” Artificial Intelligence, 31, 3 (1987), pp. 355–395.
[12] Lowe, David G., “Fitting parameterized three-dimensional models to images,” IEEE Trans. on Pattern Analysis andMachine Intelligence, 13, 5 (1991), pp. 441–450.
[13] Murase, Hiroshi, and Shree K. Nayar, “Visual learning and recognition of 3-D objects from appearance,” International Journal of Computer Vision, 14, 1 (1995), pp. 5–24.
[14] Nelson, Randal C., and Andrea Selinger, “Large-scale tests of a keyed, appearance-based 3-D object recognition system,” Vision Research, 38, 15 (1998), pp. 2469–88.
[15] Ohba, Kohtaro, and Katsushi Ikeuchi, “Detectability, uniqueness, and reliability of eigen windows for stable verification of partially occluded objects,” IEEE Trans. on Pattern Analysis and Machine Intelligence, 19, 9 (1997),pp. 1043–48.
[16] Perrett, David I., and Mike W. Oram, “Visual recognition based on temporal cortex cells: viewer-centered processing of pattern configuration,” Zeitschrift f¨ur Naturforschung C, 53c (1998), pp. 518–541.
[17] Pope, Arthur R. and David G. Lowe, “Learning probabilistic appearance models for object recognition,” in Early VisualLearning, eds. ShreeNayar and Tomaso Poggio (Oxford University Press, 1996), pp. 67–97.
[18] Schiele, Bernt, and James L. Crowley, “Object recognition using multidimensional receptive field histograms,” Fourth European Conference on Computer Vision, Cambridge, UK (1996), pp. 610–619.
[19] Schmid, C., and R. Mohr, “Local grayvalue invariants for image retrieval,” IEEE PAMI, 19, 5 (1997), pp. 530–534.
[20] Swain, M., and D. Ballard, “Color indexing,” International Journal of Computer Vision, 7, 1 (1991), pp. 11–32.
[21] Tanaka, Keiji, “Mechanisms of visual object recognition: monkey and human studies,”Current Opinion in Neurobiology, 7 (1997), pp. 523–529.
[22] Treisman, Anne M., and Nancy G. Kanwisher, “Perceiving visually presented objects: recognition, awareness, and modularity,”Current Opinion in Neurobiology, 8 (1998), pp.218–226.
[23] Zhang, Z., R. Deriche, O. Faugeras, Q.T. Luong, “A robust technique for matching two uncalibrated images through the recovery of the unknown epipolar geometry,” Artificial Intelligence, 78, (1995), pp. 87-119.