为什么拉普拉斯算子具有旋转不变性

看《图像局部不变性特征与描述》遇到的issue

基本理论:

拉普拉斯算子是最简单的各向同性微分算子，具有旋转不变性。一个二维图像函数 的拉普拉斯变换是各向同性的二阶导数:

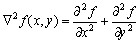
为了更适合于数字图像处理，将该方程表示为离散形式：

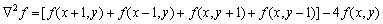
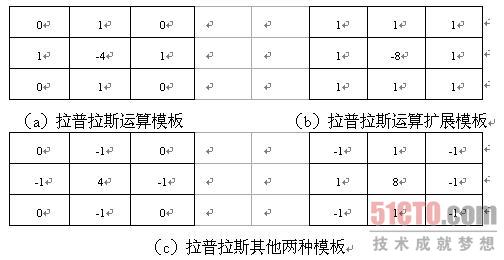
另外，拉普拉斯算子还可以表示成模板的形式，如下图所示。图（a）表示离散拉普拉斯算子的模板，图（b）表示其扩展模板，图（c）则分别表示其他两种拉普拉斯的实现模板。从模板形式容易看出，如果在图像中一个较暗的区域中出现了一个亮点，那么用拉普拉斯运算就会使这个亮点变得更亮。因为图像中的边缘就是那些灰度发生跳变的区域，所以拉普拉斯锐化模板在边缘检测中很有用。一般增强技术对于陡峭的边缘和缓慢变化的边缘很难确定其边缘线的位置。但此算子却可用二次微分正峰和负峰之间的过零点来确定，对孤立点或端点更为敏感，因此特别适用于以突出图像中的孤立点、孤立线或线端点为目的的场合。同梯度算子一样，拉普拉斯算子也会增强图像中的噪声，有时用拉普拉斯算子进行边缘检测时，可将图像先进行平滑处理。

图像锐化处理的作用是使灰度反差增强，从而使模糊图像变得更加清晰。图像模糊的实质就是图像受到平均运算或积分运算，因此可以对图像进行逆运算，如微分运算能够突出图像细节，使图像变得更为清晰。由于拉普拉斯是一种微分算子，它的应用可增强图像中灰度突变的区域，减弱灰度的缓慢变化区域。因此，锐化处理可选择拉普拉斯算子对原图像进行处理，产生描述灰度突变的图像，再将拉普拉斯图像与原始图像叠加而产生锐化图像。拉普拉斯锐化的基本方法可以由下式表示：

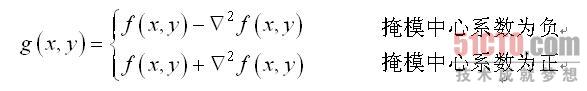
这种简单的锐化方法既可以产生拉普拉斯锐化处理的效果，同时又能保留背景信息，将原始图像叠加到拉普拉斯变换的处理结果中去，可以使图像中的各灰度值得到保留，使灰度突变处的对比度得到增强，最终结果是在保留图像背景的前提下，突现出图像中小的细节信息。

将原始图像通过拉普拉斯变换后增强了图像中灰度突变处的对比度，使图像中小的细节部分得到增强并保留了图像的背景色调，使图像的细节比原始图像更加清晰。基于拉普拉斯变换的图像增强已成为图像锐化处理的基本工具。

 

1.数学证明

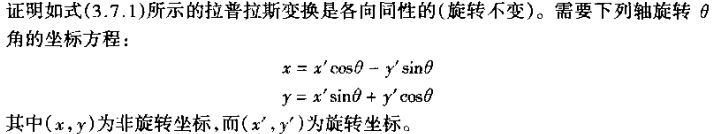
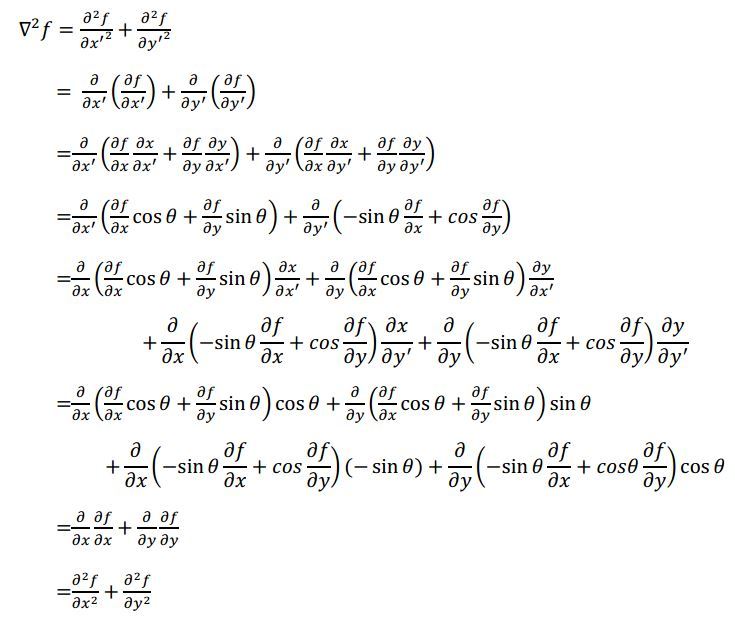
2.利用图像证明

可以看出 拉普拉斯算子为周边四个元素和减去中间元素，也可以添加对角的45度方向的，则就是周边8个元素减去中间的元素。但是通常是会用中间元素减去周边元素。可以看出与周边的元素的顺序无关，即旋转不变性

 

高斯拉普拉斯算子的卷积模板

 

 Laplacian of Gaussian Operator是用于边缘检测的算子,

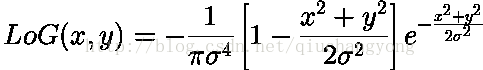
它常用的卷积模板有:

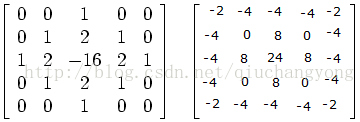
总结为：
1. 卷积模板都是由整数元素构成的矩阵。卷积是乘法运算的累积，整数乘法比浮点数效率高。
2. 该卷积模板具有最大的对称性。表现为其不只是检测某一个方向的边缘，而是所有可能的方向的边缘。
3. 该卷积模板的所有元素和为0，即如果是平滑的纹理，也不应该被检测出来。
4. 实际上卷积模板里的整数是近似值，是一种逼近后的结果，它不是简单地round，floor或ceiling函数处理后的结果，需要考虑2和3的约束。也许你会说这样做与LoG函数给出的数值不精确成比例，但实际上这关系不大。上图中左边是使用的高斯标准差为0.5，右边的使用的高斯标准差为1.0，逼近后的结果。