线段树(三)
一、线段树的定义
线段树,又名区间树,是一种二叉搜索树。
那么问题来了,啥是二叉搜索树呢?
对于一棵二叉树,若满足:
①它的左子树不空,则左子树上所有结点的值均小于它的根结点的值
②若它的右子树不空,则右子树上所有结点的值均大于它的根结点的值
③它的左、右子树也分别为二叉搜索树
那么这就是一棵二叉搜索树。
扯完废话,再回到线段树这里。顾名思义,线段树就是由线段构成的树,它大概长成这样: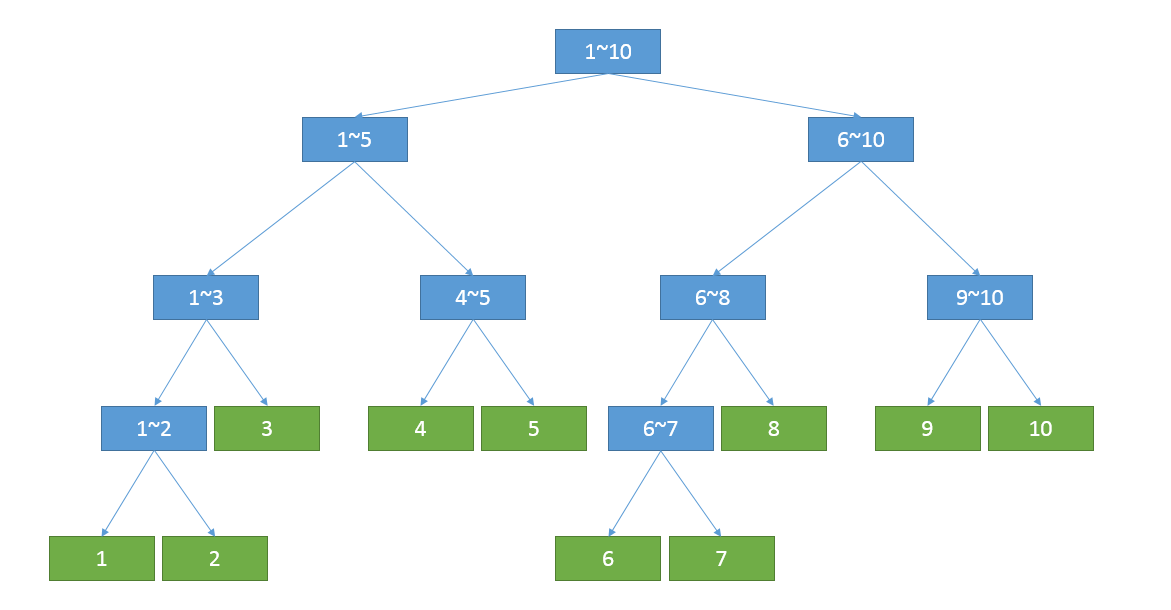
对于每一棵线段树上的节点,都有三个值:左区间、右区间以及权值。(当然,在某些情况下它只有左右区间,这个时候线段树只是作为维护某个值而使用的数据结构,如扫描线)
线段树有一个非常重要的性质,就是当父亲节点的区间为[x,y]时,左孩子的区间就必定为[x,(x+y)/2],右孩子的区间必定为[(x+y)/2+1,y]
二、线段树的基本操作
常见的应用在竞赛中的操作分为:建树,单点修改,区间求和,查询区间最值,区间修改
我们先从建树开始讲起。
1.线段树的建树
线段树的建树是采用递归写法来构建的。其核心思想就是:
递归左子树,递归左子树的左子树...递归到左子树的叶子结点,然后回溯到叶子结点的父节点的右子树...以此类推。在每一次递归到叶子结点的时候就给该节点赋值(输入或者0之类的)。
建树的伪代码很容易得出:
1 void Build() {
2 if(是叶子节点) 赋值
3 else {
4 递归左子树;
5 递归右子树;
6 }
7 }
那么问题出在这里:怎么判断是叶子结点?怎么递归左右子树?现在,往上翻,看看线段树的性质。至于叶子节点的判断,我们也可以利用线段树的性质。叶子结点没有子节点,那么它的左右区间必定相同(即一个点而不是一条线段),否则可以继续向下递归。
另外,线段树是一棵满二叉树,所以满足满二叉树一个性质:父亲节点编号为a,那么左子树编号为2*a,右子树编号为2*a+1
知道了这些性质,建树就很好写了。
1 /*i表示当前递归编号,l,r分别表示当前点的左右区间*/
2 /*Tree数组是存储线段树的数组*/
3 void Build(int i, int l, int r) {
4 if(l == r) {
5 scanf("%d", Tree[i])
6 return;
7 }
8 int Mid = (l + r) / 2;
9 Build(i * 2, l, Mid);
10 Build(i * 2, Mid + 1, r);
11 PushUp(i) /*这是什么?往后看*/
12 }
怎么样?很简单吧!
2.线段树的单点修改
接下来来讲讲线段树最基本操作之一 -- 单点修改。(前面讲了怎么递归左右子树,这里不再赘述)
单点修改在题目中一般以 "给定两个数A, B,将树上第A个修改为B"的形式存在。你可能认为:"这不是很Easy吗?",然后立马敲下了这一段代码。
Tree[A] = B
这么写就大错特错了!因为这里的"Tree[A]"不一定是我们需要找的那个'A',这么写的话会导致整棵树结构被打乱。
特别提醒:线段树中的修改操作一定只能使用特别的操作来完成,千万不要自以为是的写一些似乎是对的代码
那么怎么做呢?我们来分析一下。
如果要找到这个点A,我们必须要递归左右子树来寻找。上面介绍了递归的方法,大家是否已经发现了这样的递归很像某一种算法?没错,就是分治(如果要理解成二分也没有问题),那么问题就很显然了,每次都二分,如果要寻找的点A在当前区间的中点,即(l+r)/2之前,就递归左子树,否则递归右子树。那么写成伪代码是这样的
void Quary_Single() {
if(找到改点) 修改
if(查找点在当前区间前半部分) 递归左子树
else 递归右子树
}
这些操作我都介绍过了,那么写成真正的代码也不会很难吧。
1 /*i为当前编号,L,R为左右区间,A为修改点的编号,B为修改的值*/
2 void Update_Single(int i, int L, int R, int A, int B) {
3 if(L == R) {
4 /*如果找到了,修改值*/
5 Tree[i] == B;
6 return;
7 }
8 int Mid = (L + R) / 2;
9 if(A <= Mid) Update_Single(i * 2, L, Mid, A, B); /*递归左子树*/
10 else Update_Single(i * 2 + 1, Mid + 1, R, A, B); /*递归右子树*/
11 PushUp(i); /*这是什么?往后看*/
12 }
大家应该都有一个想法吧:单点修改也不过如此。
的确,不过如此
3.线段树的区间求和
首先我要介绍一个东西,叫做 "PushUp"函数。这个函数的作用是什么呢?应该有很多人都想到了,就是将子节点的信息"传"给父亲节点。具体写起来也不难,我们可以将PushUp函数当做前缀和来处理(其实方便区间和,如果要求区间最值,PushUp函数就是处理最值了)
代码大约是这样:
/*区间最值处理*/
void PushUp(int Now) {
Tree[Now] = Max(Tree[Now * 2], Tree[Now * 2 + 1]);
}
/*区间和处理*/
void PushUp(int Now) {
Tree[Now] = Tree[Now * 2] + Tree[Now * 2 + 1];
}
这个东西要在什么地方加上呢?要在建树以及修改之后,也就是上述的两个操作之后。。
那么来讲讲区间求和问题吧。区间求和其实非常简单,我们只需要查询给定的区间,然后找到这个区间里面的所有叶子结点,把叶子结点的权值加起来,得到的结果就是我们所需要的区间和。那么要PushUp干嘛呢?PushUp简化了这个过程。在原本的操作里,最差的情况是要递归一直到叶子结点,多么令人心痛的浪费时间!然而我们用PushUp预处理之后,就变成了前缀和问题,求和不就是小菜一碟吗?
给出伪代码
int Quary_Total() {
if(在查询区间内) 返回当前权值
if(当前区间中点在查询区间的右边) 遍历左子树,并求和
if(当前区间中点在查询区间的左边) 遍历右子树,并求和
return 答案
}
真代码不需要我多说了吧。
1 /*i 为当前编号, L, R为查询区间*/
2 int Quary_Total(int i, int L, int R, int l, int r) {
3 if(l >= L && r <= R) return Tree[i]; /*如果在区间内*/
4 int Mid = (L + R) / 2, Cnt = 0; /*初始化*/
5 if(L <= Mid) Cnt += Quary_Total(i * 2, L, R, l, Mid); /*递归左子树*/
6 if(R > Mid) Cnt += Quary_Total(i * 2 + 1, L, R, Mid + 1, r); /*递归右子树*/
7 return Cnt;
8 }
就是这么简单。
4.线段树的区间最值
其实区间最值完全可以放在区间和里面讲的,因为写法几乎一样,唯一不同的是PushUp的方式以及判断的方式。因为在PushUp的时候预处理每一棵子树的最值,所以真正处理区间时只要把上面一层扫过去就可以了。
真代码直接上:)
int Quary_RMQ(int i, int L, int R, int l, int r) {
if(l >= L && r <= R) return Tree[i];
int Mid = (L + R) / 2, Cnt = 0;
int A, B;
A = Quary_RMQ(i * 2, L, R, l, Mid);
B = Quary_RMQ(i * 2 + 1, L, R, Mid + 1, R);
return Max(A, B); /*返回最大值*/
}
那么线段树的四大基本操作就这么讲完了
三、线段树的优势和劣势
线段树的优势和劣势都很明显。
优势:时间快,操作多
线段树的优势首先是时间快,上文也讲过,线段树的所有操作都是基于分治算法,再经过PushUp优化,整个算法就变得十分稳定。比起一般的数组暴力算法,线段树是明显更优的。看下表就知道
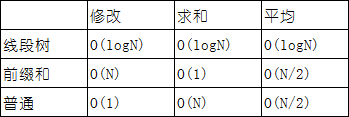
当然,在一些时候它也会劣于下面两种算法,不过是在极少数时候。
另外,它操作多样化,比起树状数组,多了区间最值一种操作。
劣势:空间浪费
上面也介绍过了,线段树一直是一棵满二叉树,所以无论如何,它所开的空间必须是四倍。但是在某些情况,线段树会浪费三倍的空间(只有一条链等),但你又不能省掉这三倍空间,还是得苦逼的开四倍。
和树状数组比起来,一棵普通的线段树是树状数组空间的四倍。
四、总结
线段树是一种区间存储结构,操作基本都有一个固定的模板,所以对于OIer的编码能力要求并不强,只要掌握了,基本就是小菜一碟。只要注意空间上的问题,其他都没什么困难的。
转自:http://www.cnblogs.com/xiaoyao24256/p/6590885.html




