转自:http://blog.csdn.net/liujian20150808/article/details/51137749
1.线段树的定义:
线段树是一种二叉搜索树,与区间树相似,它将一个区间划分成一些单元区间,每个单元区间对应线段树中的一个叶结点。
对于线段树中的每一个非叶子节点[a,b],它的左儿子表示的区间为[a,(a+b)/2],右儿子表示的区间为[(a+b)/2+1,b]。因此线段树是平衡二叉树,最后的子节点数目为N,即整个线段区间的长度。
举例描述:
因此有了以上对线段树的定义,我们可以将区间[1,10]的线段树结构描述出来:

图片来自于百度百科
有了线段[1,10]的线段树结构,我们可以发现,每个叶节点对应区间范围内的端点[a,a](1<=a<=10)
2.构造线段树
显然,当我们将线段树定义清楚之后,那么我们就要想要怎么去实现它。
我们可以观察上图,对于线段树中的每一个非叶子节点[a,b],它的左儿子表示的区间均为[a,(a+b)/2],右儿子表示的区间均为[(a+b)/2+1,b],
因此我们利用线段树的这一特点,可以递归的将这棵线段树构造出来,递归的终止条件也就是我们构造到了叶节点,即此时线段的左右区间相等。
有了以上的思路,我们可以得出以下构造线段树的代码:
-
- Node *Build(Node *_root,int left,int right){
- _root = Init(_root,left,right);
- if(left != right){
- _root -> lchild = Build(_root -> lchild,left,(left + right) / 2);
- _root -> rchild = Build(_root -> rchild,(left + right)/2+1,right);
- }
- return _root;
- }
为了检验构造情况是否和上述图示一致,我们可以利用树的中序遍历,查看每个节点存储的线段,因此我们得出以下完整代码:
- #include<cstdio>
- #include<cstdlib>
-
- typedef struct node Node;
-
- struct node{
- int leftvalue;
- int rightvalue;
- Node *lchild;
- Node *rchild;
- };
-
- int flag = 1;
- Node *Init(Node *_node,int lvalue,int rvalue){
- _node = (Node *)malloc(sizeof(Node));
- _node -> lchild = NULL;
- _node -> rchild = NULL;
- _node -> leftvalue = lvalue;
- _node -> rightvalue = rvalue;
- return _node;
- }
-
-
- Node *Build(Node *_root,int left,int right){
- _root = Init(_root,left,right);
- if(left != right){
- _root -> lchild = Build(_root -> lchild,left,(left + right) / 2);
- _root -> rchild = Build(_root -> rchild,(left + right)/2+1,right);
- }
- return _root;
- }
-
-
- void inorder(Node *_node){
- if(_node){
- inorder(_node -> lchild);
- printf("第%d个遍历的节点,存储区间为:[%d,%d]\n",flag++,_node -> leftvalue,_node -> rightvalue);
- inorder(_node -> rchild);
- }
- }
-
- int main(){
- Node *root;
- root = Build(root,1,10);
- inorder(root);
- return 0;
- }
运行结果:

我们发现,存储的结果与一开始定义的完全一致,于是我们便成功的建立好了一棵空的线段树。
3.线段树的一些简单应用:
(1).区间查询问题:
RMQ(Range Minimum/Maximum Query),即区间最值查询,是指这样一个问题:对于长度为n的数列A,回答若干询问RMQ(A,i,j)(i,j<=n),返回数列A中下标在i,j之间的最小/大值。
我们以RMQ为例:即在给定区间内查询最小值,假设我们已经将对应区间的最小值存入了线段树的节点中,那么我们利用刚刚建立好的线段树来解决这一问题。
如果查询的区间是[1,2],[3,3]这样的区间,那么我们直接找到对应节点解决这一问题即可。但是如果查询的区间是[1,6],[2,7]这样的区间时,我们可以发现在线段树中,无法找到这样的节点,
但是呢,我们可以找到树中哪几个节点能够组成我们所要求的区间,然后再取这几个区间内的最小值不就解决问题了吗?
因此有了这样的想法,我们对于任何在合理范围内的查询,都可以找到若干个相连的区间,然后将这若干个区间合并,得到待求的区间。
通常,我们用来寻找这样的一个区间的简单办法是:
function 在节点v查询区间[l,r]
if v所表示的区间和[l,r]交集不为空集 if v所表示的区间完全属于[l,r]
选取v
else
在节点v的左右儿子分别查询区间[l,r]end if end if
end function
伪代码出自《线段树》讲稿 杨戈
因此根据以上伪代码我们可以得出以下完整代码:
- #include<cstdio>
- #include<cstdlib>
-
- typedef struct node Node;
-
- struct node{
- int leftvalue;
- int rightvalue;
- Node *lchild;
- Node *rchild;
- };
-
- int flag = 1;
- Node *Init(Node *_node,int lvalue,int rvalue){
- _node = (Node *)malloc(sizeof(Node));
- _node -> lchild = NULL;
- _node -> rchild = NULL;
- _node -> leftvalue = lvalue;
- _node -> rightvalue = rvalue;
- return _node;
- }
-
-
- Node *Build(Node *_root,int left,int right){
- _root = Init(_root,left,right);
- if(left != right){
- _root -> lchild = Build(_root -> lchild,left,(left + right) / 2);
- _root -> rchild = Build(_root -> rchild,(left + right)/2+1,right);
- }
- return _root;
- }
-
-
- void inorder(Node *_node){
- if(_node){
- inorder(_node -> lchild);
- printf("第%d个遍历的节点,存储区间为:[%d,%d]\n",flag++,_node -> leftvalue,_node -> rightvalue);
- inorder(_node -> rchild);
- }
- }
-
- void Query(Node *_node,int left,int right){
-
- if(right >= _node -> leftvalue && left <= _node -> rightvalue){
-
- if(left <= _node -> leftvalue && right >= _node -> rightvalue){
- printf("[%d,%d]\n",_node -> leftvalue,_node -> rightvalue);
- }
- else{
- Query(_node -> lchild,left,right);
- Query(_node -> rchild,left,right);
- }
- }
-
- }
-
- int main(){
- Node *root;
- root = Build(root,1,10);
- inorder(root);
- printf("区间[2,7]由线段树中以下区间构成:\n");
- Query(root,2,7);
- return 0;
- }
我们以区间[2,7]为例,得出以下运行结果:

(2).区间修改操作:
在这里我们依然以RMQ问题为例,假如一开始的时候,线段树中每个节点的权值都是1,那么现在我要做的是,指定一个合法的区间,然后对这个区间内所有的数加上或者减去某个数,如果我们按照区间的内的数一 一的
去遍历并修改线段树的节点的话,那么改动的节点数必然远远超过O(logn)个,而且会存在大量的重复遍历操作,那么要怎么样才能提高程序的效率呢?
首先,我们考虑给定的修改区间,按照前面我们讨论过的问题,我们可以把待操作区间变成几个相连的子区间,那么我们试想,当我们要修改一个给定区间时,我们对其所有子区间进行修改,这样的话不就把整个
待修改区间处理完毕了吗?这样的话我们是否可以只通过修改几个子区间节点的值,而不考虑它们的孩子节点,就完成所有的操作了呢?
实际上,如果不考虑这些子区间的孩子节点的话,是错误的,因为在父亲节点所带的权值发生变化时,比如说上图示中区间[1,2]中每个值都加上5,那么我们把线段树中表示区间[1,2]的节点修改完毕是否就可以了呢?
答案显然是错误的,因为该节点的左孩子([1,1])和右孩子节点所表示的区间([2,2])中的值也都发生了变化。
所以在这里我们为了方便,我们在节点定义中加入一个标记的量,用来存储对节点的修改情况。显然,当我们自上而下的访问某节点时,父亲节点的标记要"传给"孩子节点,即修改大的区间,其子区间也必然被改动。
有了以上的分析,我们可以总结操作:
首先找到树中哪几个节点表示的区间,能够组成我们待修改的区间,然后从这些节点开始向下遍历,将以这些节点为根节点的子树节点权值做相应的改变。(边查找对应子区间,边修改权值)
完整代码如下:
- #include<cstdio>
- #include<cstdlib>
-
- typedef struct node Node;
-
- struct node{
- int leftvalue;
- int rightvalue;
- Node *lchild;
- Node *rchild;
- int weight;
- int mark;
- };
-
- int flag = 1;
- Node *Init(Node *_node,int lvalue,int rvalue){
- _node = (Node *)malloc(sizeof(Node));
- _node -> lchild = NULL;
- _node -> rchild = NULL;
- _node -> leftvalue = lvalue;
- _node -> rightvalue = rvalue;
- _node -> weight = 1;
- _node -> mark = 0;
- return _node;
- }
-
-
- Node *Build(Node *_root,int left,int right){
- _root = Init(_root,left,right);
- if(left != right){
- _root -> lchild = Build(_root -> lchild,left,(left + right) / 2);
- _root -> rchild = Build(_root -> rchild,(left + right)/2+1,right);
- }
- return _root;
- }
-
-
- void inorder(Node *_node){
- if(_node){
- inorder(_node -> lchild);
- printf("\n第%d个遍历的节点,存储区间为:[%d,%d]\n",flag,_node -> leftvalue,_node -> rightvalue);
- printf("\n第%d个遍历的节点,权值为%d,标记为%d\n",flag++,_node -> weight,_node -> mark);
- inorder(_node -> rchild);
- }
- }
-
- void Query(Node *_node,int left,int right){
-
- if(right >= _node -> leftvalue && left <= _node -> rightvalue){
-
- if(left <= _node -> leftvalue && right >= _node -> rightvalue){
- printf("[%d,%d]\n",_node -> leftvalue,_node -> rightvalue);
- }
- else{
- Query(_node -> lchild,left,right);
- Query(_node -> rchild,left,right);
- }
- }
-
- }
-
-
- void change(Node *node){
- if(node){
- if(node -> lchild){
- node -> lchild -> mark += node -> mark;
- node -> lchild -> weight += node -> lchild -> mark;
- change(node -> lchild);
- }
- if(node -> rchild){
- node -> rchild -> mark += node -> mark;
- node -> rchild -> weight += node -> rchild -> mark;
- change(node -> rchild);
- }
- }
- }
-
- void update(Node *node,int left,int right,int pos){
-
-
- if(right >= node -> leftvalue && left <= node -> rightvalue){
- if(left <= node -> leftvalue && right >= node -> rightvalue){
- node -> mark = pos;
- node -> weight += node -> mark;
-
- change(node);
- }
- else{
- update(node -> lchild,left,right,pos);
- update(node -> rchild,left,right,pos);
- }
- }
- }
-
-
-
- int main(){
- Node *root;
- root = Build(root,1,4);
-
- update(root,1,3,5);
- inorder(root);
- return 0;
- }
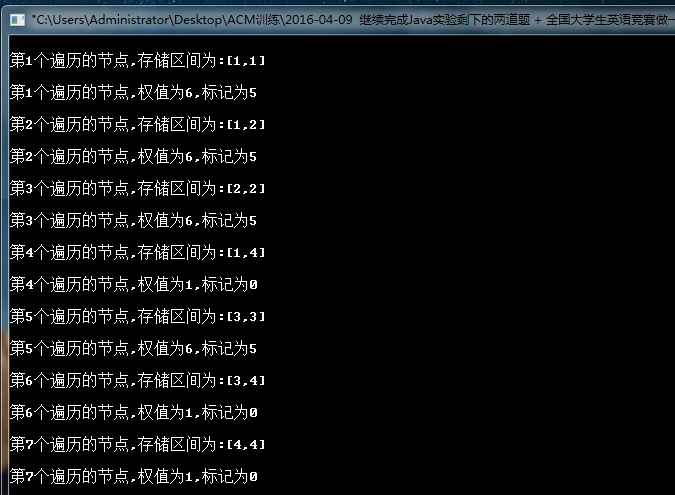
运行结果: