机器学习(4): KNN 算法
1. 综述



from sklearn import datasets
from collections import Counter # 为了做投票
from sklearn.model_selection import train_test_split
import numpy as np
# 导入iris数据
iris = datasets.load_iris()
X = iris.data
y = iris.target
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=2003)
def euc_dis(instance1, instance2):
"""
计算两个样本instance1和instance2之间的欧式距离
instance1: 第一个样本, array型
instance2: 第二个样本, array型
"""
# TODO
dist = np.sqrt(sum((instance1 - instance2)**2))
return dist
def knn_classify(X, y, testInstance, k):
"""
给定一个测试数据testInstance, 通过KNN算法来预测它的标签。
X: 训练数据的特征
y: 训练数据的标签
testInstance: 测试数据,这里假定一个测试数据 array型
k: 选择多少个neighbors?
"""
# TODO 返回testInstance的预测标签 = {0,1,2}
#时间复杂度 O(N): N:number of samples
distances = [euc_dis(x, testInstance) for x in X] #若N很大,计算欧式距离消耗的测试时间非常大的时间,take forever~ (KNN的缺点)
#argsort: O(NlogN)
#如何优化? priority queue O(NlogK)
kneighbors = np.argsort(distances)[:k]
count = Counter(y[kneighbors])
#print(count)可以显示出来每个样本出现了多少次
return count.most_common()[0][0]#取出出现最多的值
# 预测结果。
predictions = [knn_classify(X_train, y_train, data, 3) for data in X_test]
correct = np.count_nonzero((predictions==y_test)==True)
#accuracy_score(y_test, clf.predict(X_test))
print ("Accuracy is: %.3f" %(correct/len(X_test)))
Accuracy is: 0.921
https://zhuanlan.zhihu.com/p/71785246
kNN 的花式用法
kNN (k-nearest neighbors)作为一个入门级模型,因为既简单又可靠,对非线性问题支持良好,虽然需要保存所有样本,但是仍然活跃在各个领域中,并提供比较稳健的识别结果。
说到这里也许你会讲,kNN 我知道啊,不就是在特征空间中找出最靠近测试样本的 k 个训练样本,然后判断大多数属于某一个类别,那么将它识别为该类别。
这就是书上/网络上大部分介绍 kNN 的说辞,如果仅仅如此,我也不用写这篇文章了。事实上,kNN 用的好,它真能用出一朵花来,越是基础的东西越值得我们好好玩玩,不是么?
第一种:分类
避免有人不知道,还是简单回顾下 kNN 用于分类的基本思想。
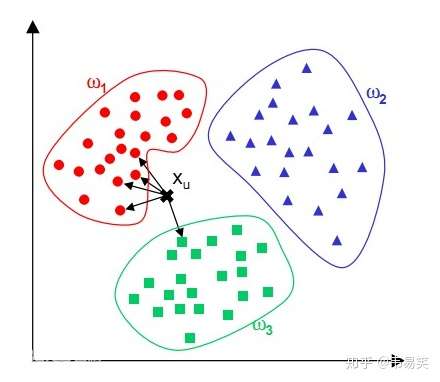
针对测试样本 Xu,想要知道它属于哪个分类,就先 for 循环所有训练样本找出离 Xu 最近的 K 个邻居(k=5),然后判断这 K个邻居中,大多数属于哪个类别,就将该类别作为测试样本的预测结果,如上图有4个邻居是红色,1是绿色,那么判断 Xu 的类别为“红色”。
第二种:回归
根据样本点,描绘出一条曲线,使得到样本点的误差最小,然后给定任意坐标,返回该曲线上的值,叫做回归。那么 kNN 怎么做回归呢?
你有一系列样本坐标(xi, yi),然后给定一个测试点坐标 x,求回归曲线上对应的 y 值。用 kNN 的话,最简单的做法就是取 k 个离 x 最近的样本坐标,然后对他们的 y 值求平均:
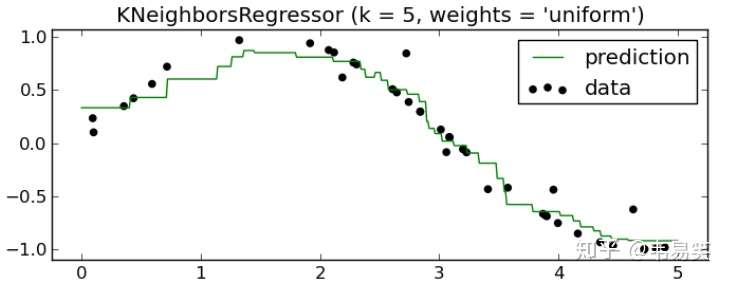
绿色是拟合出来的曲线,用的是 sklearn 里面的 KNeighborsRegressor,可以看得出对非线性回归问题处理的很好,但是还可以再优化一下,k 个邻居中,根据他们离测试点坐标 x 的距离 d 的倒数 1/d 进行加权处理:
w = [ 1 / d[i] for i in range(k) ]
y = sum([ (w[i] * y[i]) for i in range(k) ]) / sum(w)如果 x 刚好和某样本重合,di = 0 的话,1/d 就正无穷了,那么接取该样本的 y 值,不考虑其他点(sklearn的做法),这样得到的 Y 值就相对比较靠谱了:
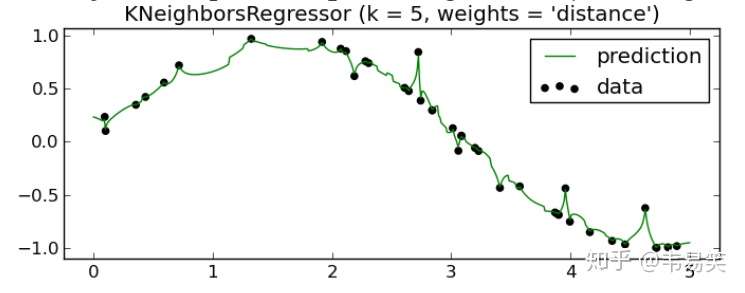
这样误差就小多了,前面不考虑距离y值平均的方法在 sklearn 中称为 uniform,后一种用距离做权重的称为 distance。
这曲线拟合的效果非常漂亮,你用梯度下降或者最小二乘法做拟合根本达不到这样的效果,即便支持向量回归 SVR 也做不到这么低的误差率。如果你觉得有些过拟合的话,可以调节 K 的值,比如增加 K 值,可以让曲线更加平滑一些。
更好的做法是 wi 设置为 exp(-d) ,这样 d=0 的时候取值 1,d 无穷大的时候,接近 0:
w[i] = math.exp(-d[i])这样即 x 和某个训练样本重合或者非常接近也不会把该 wi 弄成无穷大,进而忽略其他样本的权重,避免了 sklearn 里面那种碰到离群点都非要过去绕一圈的问题,曲线就会更平滑。
第三种:One-class 识别
One-class 分类/识别又称为:异常点/离群点检测,这个非常有用。假设我们的 app 需要识别5种不同的用户手势,一般的分类器只会告诉你某个动作属于 1-5 哪个类型,但是如果是用户进行一些非手势的普通操作,我们需要识别出来“不属于任何类型”,然后需要在手势模块中不进行任何处理直接忽略掉。
这个事情用传统分类器非常困难,因为负样本是无穷多,多到没法列举所有额外的手势,我们只能收集正样本。这和 0-9 数字手写识别是一样的,比如用户写了个 A 字母,我们需要判断某个输入图像不是 0-9 中任何一个,但是我们除了 0-9 的样本外没法枚举所有例外的可能。
这时候 One-class 识别器一直扮演着举足轻重的作用,我们将 0-9 的所有样本作为“正样本”输入,测试的时候检测检测测试值是否也属于同类别,或者属于非法的负类别。kNN 来做这件事情是非常容易的,我们用 NN-d 的本地密度估计方法:
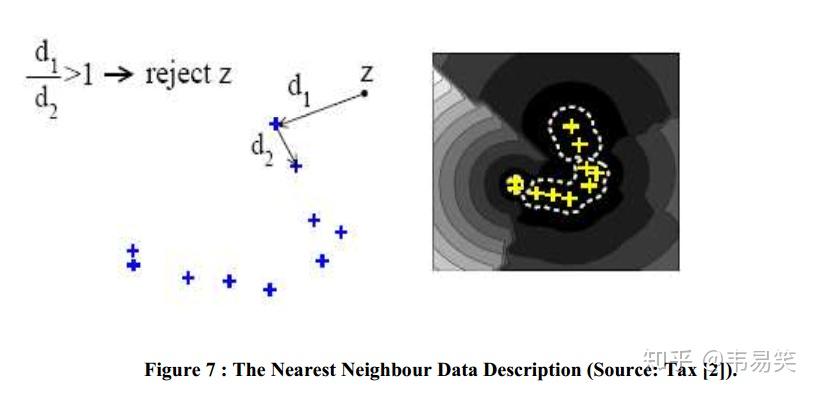
方法是对待测试样本 z ,现在训练样本中找到一个离他最近的邻居 B,计算 z 到 b 点的距离为 d1,然后再在训练样本中找到一个离 B 最近的点 C,计算 BC 距离为 d2,如果:
d1 <= alpha * d2 # alpha 一般取 1那么接受 z 样本(识别为正类别),否则拒绝它(识别为负类别)。这个方法比较简单,但是如果局部样本太密集的话,d2 非常小,容易识别为负类别被拒绝。所以更成熟的做法是在训练样本中找到 k 个离 B 最近的样本点 C1 - Ck,然后把 d2 设置成 C1 - Ck 到 B 的距离的平均值。这个方法称为 kNN-d,识别效果比之前只选一个 C 的 NN-d 会好很多。
进一步扩展,你还可以选择 j 个离 z 最近的 B 点,用上面的方法求出 j 个结果,最后投票决定 z 是否被接受,这叫 j-kNN-d 方法,上面说到的方法就是 j = 1 的特殊情况。
对比 SVM 的 ONE_CLASS 检测方法,(j) kNN-d 有接近的识别效果,然而当特征维度增加时,SVM 的 ONE_CLASS 检测精度就会急剧下降,而 (j) kNN-d 模型就能获得更好的结果。
LIBSVM 里的三大用法:分类,回归,ONE_CLASS(离群点检测),同时也是监督学习中的三类主要问题,这里我们全部用 kNN 实现了一遍,如果你样本不是非常多,又不想引入各种包依赖,那么 kNN 是一个最简单可靠的备用方案。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号