特征重要度 WoE、IV、BadRate
1.IV的用途
IV的全称是Information Value,中文意思是信息价值,或者信息量。
我们在用逻辑回归、决策树等模型方法构建分类模型时,经常需要对自变量进行筛选。比如我们有200个候选自变量,通常情况下,不会直接把200个变量直接放到模型中去进行拟合训练,而是会用一些方法,从这200个自变量中挑选一些出来,放进模型,形成入模变量列表。那么我们怎么去挑选入模变量呢?
挑选入模变量过程是个比较复杂的过程,需要考虑的因素很多,比如:变量的预测能力,变量之间的相关性,变量的简单性(容易生成和使用),变量的强壮性(不容易被绕过),变量在业务上的可解释性(被挑战时可以解释的通)等等。但是,其中最主要和最直接的衡量标准是变量的预测能力。
“变量的预测能力”这个说法很笼统,很主观,非量化,在筛选变量的时候我们总不能说:“我觉得这个变量预测能力很强,所以他要进入模型”吧?我们需要一些具体的量化指标来衡量每自变量的预测能力,并根据这些量化指标的大小,来确定哪些变量进入模型。IV就是这样一种指标,他可以用来衡量自变量的预测能力。类似的指标还有信息增益、基尼系数等等。
IV表示一个变量的预测能力:
<=0.02,没有预测能力,不可用
0.02~0.1 弱预测性
0.1~0.2 有一定预测能力
0.2+高预测性
2.对IV的直观理解
从直观逻辑上大体可以这样理解“用IV去衡量变量预测能力”这件事情:我们假设在一个分类问题中,目标变量的类别有两类:Y1,Y2。对于一个待预测的个体A,要判断A属于Y1还是Y2,我们是需要一定的信息的,假设这个信息总量是I,而这些所需要的信息,就蕴含在所有的自变量C1,C2,C3,……,Cn中,那么,对于其中的一个变量Ci来说,其蕴含的信息越多,那么它对于判断A属于Y1还是Y2的贡献就越大,Ci的信息价值就越大,Ci的IV就越大,它就越应该进入到入模变量列表中。
3.IV的计算
前面我们从感性角度和逻辑层面对IV进行了解释和描述,那么回到数学层面,对于一个待评估变量,他的IV值究竟如何计算呢?为了介绍IV的计算方法,我们首先需要认识和理解另一个概念——WOE,因为IV的计算是以WOE为基础的。
3.1WOE
WOE的全称是“Weight of Evidence”,即证据权重。WOE是对原始自变量的一种编码形式。
要对一个变量进行WOE编码,需要首先把这个变量进行分组处理(也叫离散化、分箱等等,说的都是一个意思)。分组后,对于第i组,WOE的计算公式如下:
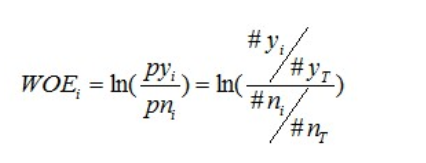
其中,pyi是这个组中响应客户(风险模型中,对应的是违约客户,总之,指的是模型中预测变量取值为“是”或者说1的个体)占所有样本中所有响应客户的比例,pni是这个组中未响应客户占样本中所有未响应客户的比例,#yi是这个组中响应客户的数量,#ni是这个组中未响应客户的数量,#yT是样本中所有响应客户的数量,#nT是样本中所有未响应客户的数量。
从这个公式中我们可以体会到,WOE表示的实际上是“当前分组中响应客户占所有响应客户的比例”和“当前分组中没有响应的客户占所有没有响应的客户的比例”的差异。
对这个公式做一个简单变换,可以得到:
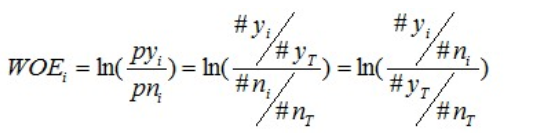
变换以后我们可以看出,WOE也可以这么理解,他表示的是当前这个组中响应的客户和未响应客户的比值,和所有样本中这个比值的差异。这个差异是用这两个比值的比值,再取对数来表示的。WOE越大,这种差异越大,这个分组里的样本响应的可能性就越大,WOE越小,差异越小,这个分组里的样本响应的可能性就越小。
关于WOE编码所表示的意义,大家可以自己再好好体会一下。
3.2 IV的计算公式
有了前面的介绍,我们可以正式给出IV的计算公式。对于一个分组后的变量,第i 组的WOE前面已经介绍过,是这样计算的:
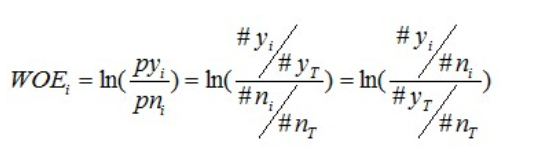
同样,对于分组i,也会有一个对应的IV值,计算公式如下:

有了一个变量各分组的IV值,我们就可以计算整个变量的IV值,方法很简单,就是把各分组的IV相加:
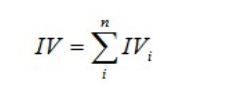
其中,n为变量分组个数。
原文链接:https://blog.csdn.net/kevin7658/article/details/50780391
==========================================
评分卡模型之特征工程中的BadRate单调与特征分箱之间的联系
Bad Rate:
坏样本率,指的是将特征进行分箱之后,每个bin下的样本所统计得到的坏样本率
bad rate 单调性与不同的特征场景:
在评分卡模型中,对于比较严格的评分模型,会要求连续性变量和有序性的变量在经过分箱后需要保证bad rate的单调性。
1. 连续性变量:
在严格的评分卡模型中,对于连续型变量就需要满足分箱后 所有的bin的 bad rate 要满足单调性,只有满足单调新的情况下,才能进行后续的WOE编码
2. 离散型变量:
离散化程度高,且无序的变量:
比如省份,职业等,我们会根据每个省份信息统计得到bad rate 数值对原始省份信息进行编码,这样就转化为了连续性变 量,进行后续的分箱操作,对于经过bad rate编码后的特征数据,天然单调。
只有当分箱后的所有的bin的bad rate 呈现单调性,才可以进行下一步的WOE编码
离散化程度低,且无序的变量:
比如婚姻状况,只有四五个状态值,因此就不需要专门进行bad rate数值编码,只要求出每个离散值对应的bin的bad rate比例是否出现0或者1的情况,若出现说明正负样本的分布存在极端情况,需要对该bin与其他bin进行合并, 合并过程完了之后 就可以直接进行后续的WOE编码
有序的离散变量:
对于学历这种情况,存在着小学,初中,高中,本科,硕士,博士等几种情况,而且从业务角度来说 这些离散值是有序的, 因此我们在分箱的时候,必须保证bin之间的有序性,再根据bad rate 是否为0 或者1的情况 决定是否进行合并,最终将合并的结果进行WOE编码
因此bad rate单调性只在连续性数值变量和有序性离散变量分箱的过程中会考虑。
bad rate要求单调性的原因分析:
1. 逻辑回归模型本身不要求特征对目标变量的单调性。之所以要求分箱后单调,主要是从业务角度考虑,解释、使用起来方便一点。如果有某个(分箱后的)特征对目标变量不单调,会加剧模型解释型的复杂化
2. 对于像年龄这种特征,其对目标变量往往是一个U型或倒U型的分布,有些公司/部门/团队是允许变量的bad rate呈(倒)U型的。
原文链接:https://blog.csdn.net/shenxiaoming77/article/details/79548807



