深度学习在CTR预估中的应用
在广告领域,预测用户点击率(Click Through Rate,简称CTR)领域近年也有大量关于深度学习方面的研究,仅这两年就出现了不少于二十多种方法
本文就近几年CTR预估领域中学术界的经典方法进行探究, 并比较各自之间模型设计的初衷和各自优缺点。
通过十种不同CTR深度模型的比较,不同的模型本质上都可以由基础的底层组件组成。
本文中出现的变量定义:
- n: 特征个数,所有特征one-hot后 连接起来的整体规模大小
- f: 特征field个数,表示特征类别有多少个
- k: embedding层维度,在FM中是隐向量维度
- H1: 深度网络中第一个隐层节点个数,第二层H2,以此类推。
二、深度学习模型
1. Factorization-machine(FM)
FM模型可以看成是线性部分的LR,还有非线性的特征组合xixj交叉而成,表示如下:
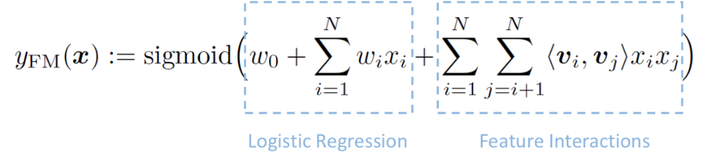
其中vi是第i维特征的隐向量,长度k<<n,包含k个描述特征的因子。参数个数为k*n。所有包含xi的非零组合特征都可以用来训练vi,缓解数据稀疏问题。
图1是从神经网络的角度表示FM, 可以看成底层为特征维度为n的离散输入,经过embedding层后,对embedding层线性部分(LR)和非线性部分(特征交叉部分)累加后输出。
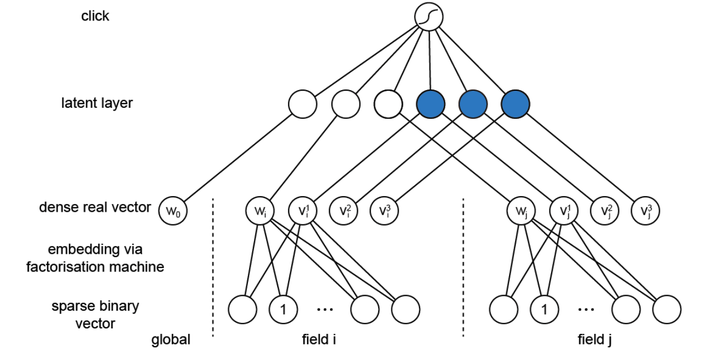
图1 FM模型结构
FM等价于FM + embedding,待学习的参数如下:
(1)LR部分: 1+n
(2)embedding 部分: n*k
FM下文中将作为各种网络模型的基础组件
2. Deep Neural Network(DNN)
图2是经典的DNN网络, 结构上看就是传统的多层感知机(MultiLayer Perceptron,简称MLP)。
在MLP网络中,输入是原始的特征n维特征空间,假设第一层隐层节点数为H1,第二层为H2,以此类推。在第一层网络中,需要学习的参数就是n*H1。
对于大多数CTR模型来说,特征体系都极其庞大而且稀疏,典型的特征数量级n从百万级到千万级到亿级甚至更高,这么大规模的n作为网络输入在ctr预估的工业界场景中是不可接受的。
下面要讲到的大多数深度学习CTR网络结构,都围绕着如何将DNN的高维离散输入,通过embedding层变成低维稠密的输入工作来展开。
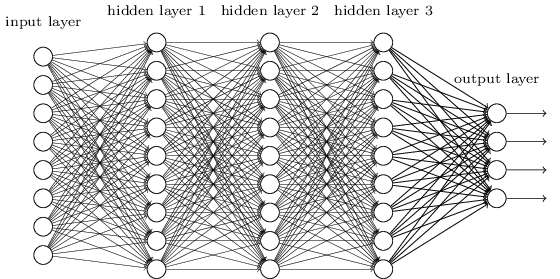
图2 DNN模型结构
DNN待学习参数: n*H1+H1*H2+H2*H3+H3*o(o为输出层大小,在ctr预估中为1)
DNN(后文称MLP)也将作为下文各种模型的基础组件之一。
3. Factorization-machine supported Neural Networks (FNN)
在上述的DNN中,网络的原始输入是全部原始特征,维度为n,通常都是百万级以上。
然而特征维度n虽然空间巨大,但如果归属到每个特征所属的field(维度为f),通常f维度会小很多。
如果有办法将每个特征用其所属的field来表示,原始输入将大大减少不少。Factorisation-machine supported Neural Networks,简称FNN就是基于这种思想提出来的。
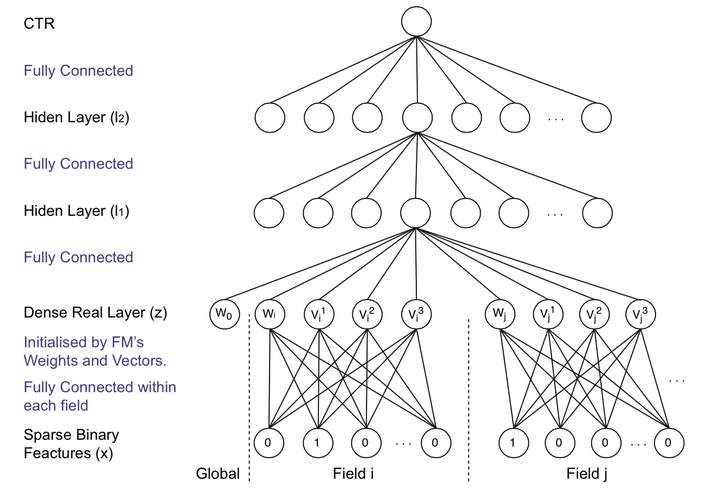
图3 FNN模型结构
FNN假设每个field有且只有一个值为1,其他均为0。x为原始输入的特征,它是大规模离散稀疏的。
它可以分成n个field,每一个field中,只有一个值为1,其余都为0(即one hot)。 field i的输入可以表示成 x[start_i: end_i], Wi为field i的embedding矩阵。
z为embedding后的向量,是一个k维的向量,它由一次项wi ,二次项vi=(vi1,vi2,…vik) 组成,其中k是FM中二次项的向量的维度。
而后面的l1,l2则为神经网络的全连接层的表示。
除此之外,FNN还具有以下几个特点:
- FM参数需要预训练
FM部分的embedding需要预先进行训练,所以FNN不是一个end-to-end模型。
在其他论文中,有试过不用FM初始化embedding, 而用随机初始化的方法,要么收敛速度很慢,要么无法收敛。
- 无法拟合低阶特征
FM得到的embedding向量直接concat连接之后作为MLP的输入去学习高阶特征表达,最终的DNN输出作为ctr预估值。因此,FNN对低阶信息的表达比较有限。
- 每个field只有一个非零值的强假设
FNN假设每个fileld只有一个值为非零值,如果是稠密原始输入,则FNN失去意义。
对于一个fileld有几个非零值的情况,例如用户标签可能有多个,一般可以做average/sum/max等处理。
本质上讲,FNN = LR+DEEP = LR + embedding + MLP,参数如下
(1)LR部分: 1+n
(2)embedding部分: n*k
(3)MLP部分: f*k*H1+H1*H2+H2
可以看到,对比DNN,在进入MLP部分之前,网络的输入由n降到了f*k(f为field个数,几十到几百之间,k为隐向量维度,一般0~100)
4. Product-based Neural Network(PNN)
FNN的embedding层直接concat连接后输出到MLP中去学习高阶特征。
PNN,全称为Product-based Neural Network,认为在embedding输入到MLP之后学习的交叉特征表达并不充分,提出了一种product layer的思想,
既基于乘法的运算来体现体征交叉的DNN网络结构,如图4所示。
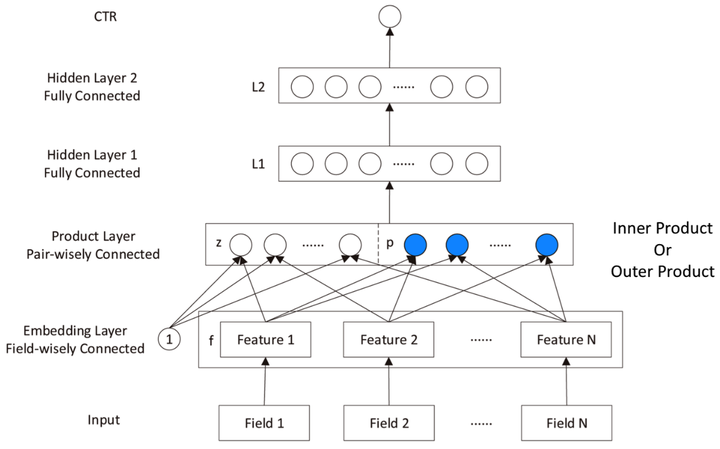
图4 PNN模型结构
对比FNN网络,PNN的区别在于中间多了一层Product Layer层。Product Layer层由两部分组成,左边z为embedding层的线性部分,右边为embedding层的特征交叉部分。
除了Product layer不同,PNN和FNN的MLP结构是一样的。这种product思想来源于,在ctr预估中,认为特征之间的关系更多是一种and“且”的关系,而非add"加”的关系。
例如,性别为男且喜欢游戏的人群,比起性别男和喜欢游戏的人群,前者的组合比后者更能体现特征交叉的意义。
根据product的方式不同,可以分为inner product(IPNN)和outer product(OPNN),如图5所示。
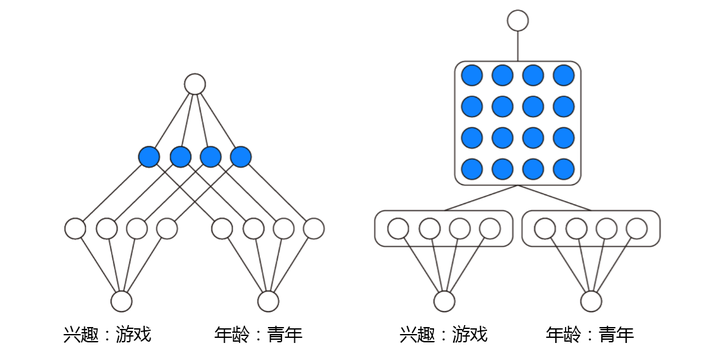
图5 PNN (左图:IPNN; 右图:OPNN)
Product layer的输出为
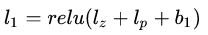
- Inner Product-based Neural Network
IPNN的叉项使用了内积g(fi, fj) = <fi, fj>。f个filed,两两求内积共计交叉项p部分的参数共f*(f-1)/2(f为特征的field个数,原始论文里用的N)个,线性部分z部分参数共f*k个。
需要学习的参数为:
(1)FM部分: 1+ n + n*k
(2)product部分: (f*k + f*(f-1)/2)*H1
(3)MLP部分:H1*H2+H2*1
- Outer Product-based Neural Network
OPNN用矩阵乘法来表示特征的交叉, g(fi, fj)=fifit。f个field两两求矩阵乘法,交叉项p共f*(f-1)/2*k*k个参数。线性部分z部分参数共f*k个。需要学习的参数为:
(1)FM部分: 1+ n + n*k
(2)product部分: (f*k + f*(f-1)/2*k*k)*H1
(3)MLP部分:H1*H2+H2*1
5. Wide & Deep Learning (Wide&Deep)
前面介绍的两种变体DNN结构FNN和PNN,都在embedding层对输入做处理后输入MLP,让神经网络充分学习特征的高阶表达,deep部分是有了,
对高阶的特征学习表达较强,但wide部分的表达是缺失的, 模型对于低阶特征的表达却比较有限。google在2016年提出了大名鼎鼎的wide&Deep的结构正是解决了这样的问题。
Wide&deep结合了wide模型的优点和deep模型的优点,网络结构如图6所示,wide部分是LR模型,Deep部分是DNN模型。
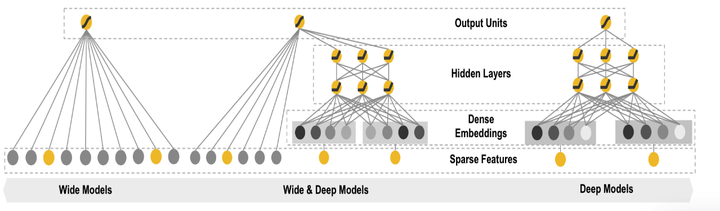
图6 Wide&Deep 模型结构
在这个经典的wide&deep模型中,google提出了两个概念,generalization(泛化性)和memory(记忆性)
- Memory(记忆性)
wide部分长处在于学习样本中的高频部分,优点是模型的记忆性好,对于样本中出现过的高频低阶特征能够用少量参数学习;
缺点是模型的泛化能力差,例如对于没有见过的ID类特征,模型学习能力较差。
- Generalization(泛化性)
deep部分长处在于学习样本中的长尾部分,优点是泛化能力强,对于少量出现过的样本甚至没有出现过的样本都能做出预测(非零的embedding向量);
缺点是模型对于低阶特征的学习需要用较多参才能等同wide部分效果,而且泛化能力强某种程度上也可能导致过拟合出现bad case.
除此之外,wide&deep模型还有如下特点
- 人工特征工程
LR部分的特征,仍然需要人工设计才能保证一个不错的效果。因为LR部分是直接作为最终预测的一部分,
如果作为wide部分的LR特征工程做的不够完善,将影响整个wide&deep的模型精度
- 联合训练
模型是end-to-end结构,wide部分和deep部分是联合训练的
- embedding层deep部分单独占有
LR部分直接作为最后输出,因此embedding层是deep部分独有的。
wide&deep 等价于LR + embedding + MLP,需要学习的网络参数有:
- LR: 1+n
- embedding部分:n*k
- MLP部分: f*k*H1 + H1*H2 + H2*1
6. Factorization-Machine based Neural Network (deepFM)
google提出的wide&deep框架固然强大,但由于wide部分是个LR模型,仍然需要人工特征工程。
但wide&deep给整个学术界和工业界提供了一种框架思想。基于这种思想,华为诺亚方舟团队结合FM相比LR的特征交叉的功能,
将wide&deep部分的LR部分替换成FM来避免人工特征工程,于是有了deepFM,网络结构如图7所示。
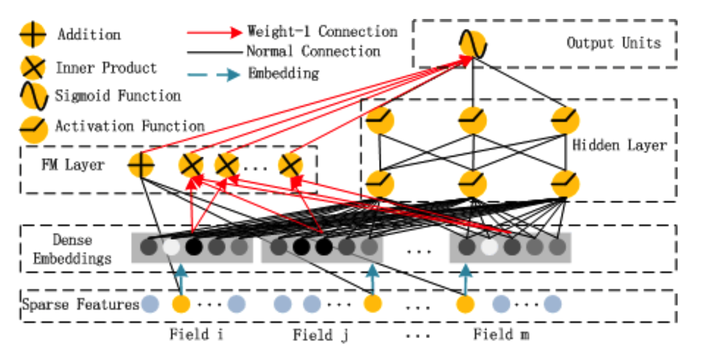
图7 DeepFM模型结构
比起wide&deep的LR部分,deepFM采用FM作为wide部分的输出,FM部分如图8所示。
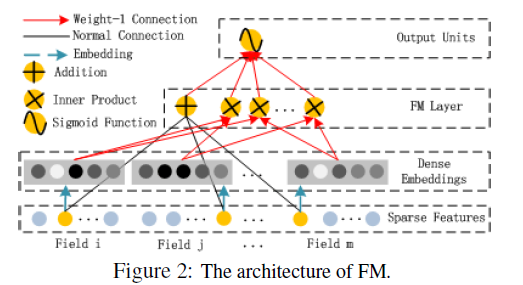
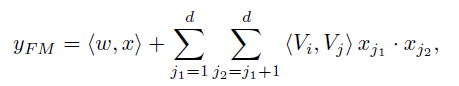
图8 deepFM模型中的FM部分结构
除此之外,deepFM还有如下特点:
- 低阶特征表达
wide部分取代WDL的LR,比FNN和PNN相比能捕捉低阶特征信息
- embedding层共享
wide&deep部分的embedding层得需要针对deep部分单独设计;
而在deepFM中,FM和DEEP部分共享embedding层,FM训练得到的参数既作为wide部分的输出,也作为DNN部分的输入。
- end-end训练
embedding和网络权重联合训练,无需预训练和单独训练
deepFM等价于FM + embedding + DNN
(1)FM部分: 1+n
(2)embedding部分:n*k
(3)DNN部分: f*k*H1 + H1*H2+H1
通过embedding层后,FM部分直接输出没有参数需要学习,进入DNN部分的参数维度从原始n维降到f*k维。
7. Neural Factorization Machines (NFM)
前面的deepFM在embedding层后把FM部分直接concat起来(f*k维,f个field,每个filed是k维向量)作为DNN的输入。
Neural Factorization Machines,简称NFM,提出了一种更加简单粗暴的方法,在embedding层后,做了一个叫做BI-interaction的操作,让各个field做element-wise后sum起来去做特征交叉,
MLP的输入规模直接压缩到k维,和特征的原始维度n和特征field 维度f没有任何关系。网络结构如图9所示。
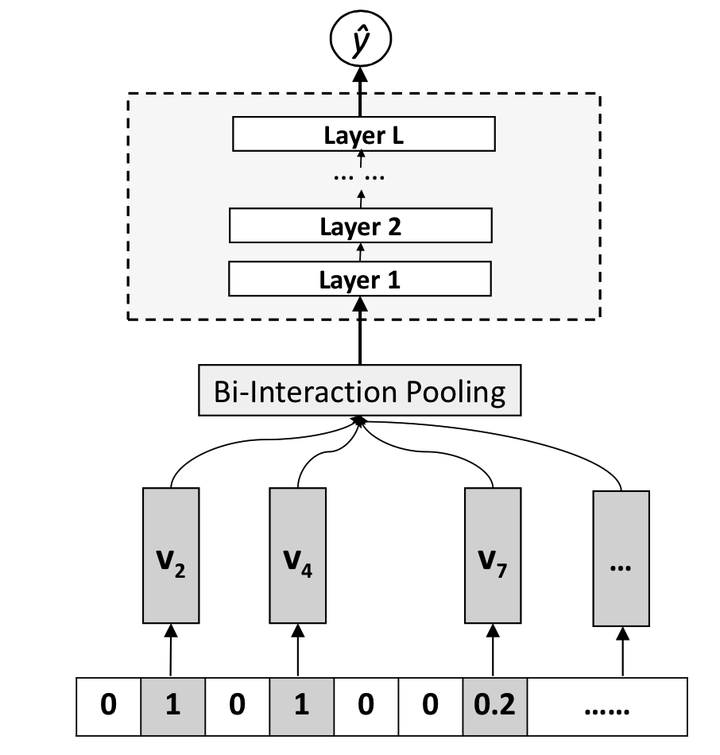
图9 NFM模型结构
这里论文只画出了其中的deep部分, wide部分在这里省略没有画出来。
Bi-interaction听名字很高大上,其实操作很简单:就是让f个field两两element-wise相乘后,得到f*(f-1)/2个向量,然后直接sum起来,最后得到一个k维的向量。
所以该层没有任何参数需要学习。
NFM等价于FM + embedding + MLP,需要学习的参数有:
(1)FM部分: 1+n
(2)embedding部分:n*k
(3)MLP部分: k*H1 + H1*H2+…+Hl*1
NFM在embedding做了bi-interaction操作来做特征的交叉处理,优点是网络参数从n直接压缩到k(比FNN和deepFM的f*k还少),降低了网络复杂度,能够加速网络的训练得到模型;但同时这种方法也可能带来较大的信息损失。
8. Attention Neural Factorization Machines (AFM)
前面提到的各种网络结构中的FM在做特征交叉时,让不同特征的向量直接做交叉,基于的假设是各个特征交叉对ctr结果预估的贡献度是一样的。
这种假设其实是不合理的, 不同特征在做交叉时,对ctr预估结果的贡献度是不一样的。Attention Neural Factorization Machines,简称NFM模型,
利用了近年来在图像、NLP、语音等领域大获成功的attention机制,在前面讲到的NFM基础上,引入了attention机制来解决这个问题。
AFM的网络结构如图10所示。和NFM一样,这里也省略了wide部分,只画出了deep部分结构。
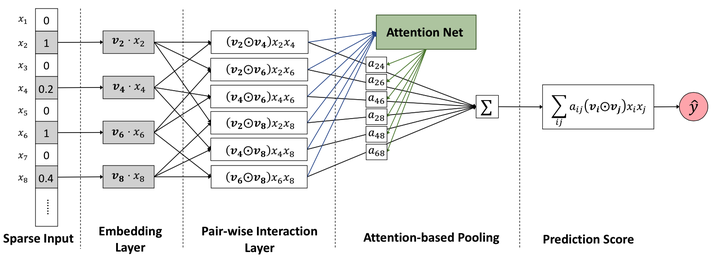
图10 AFM模型结构
AFM的embedding层后和NFM一样,先让f个field的特征做了element-wise product后,得到f*(f-1)/2个交叉项。
和NFM直接把这些交叉项sum起来不同,AFM引入了一个Attention Net,认为这些交叉特征项每个对结果的贡献是不同的,例如xi和xj的权重重要度,用aij来表示。
从这个角度来看,其实AFM其实就是个加权累加的过程。Attention Net部分的权重aij不是直接学习,而是通过如下公式表示
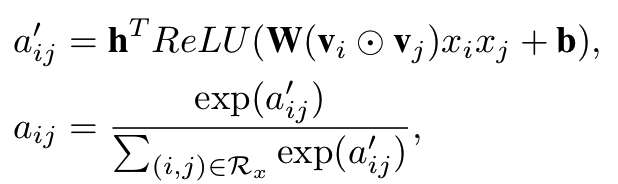
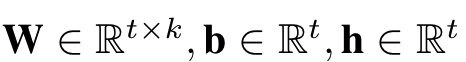
这里t表示attention net中的隐层维度,k和前面一样,为embedding层的维度。
所以这里需要学习的参数有3个,W, b, h,参数个数共t*k+2*t个。得到aij权重后,对各个特征两两点积加权累加后,得到一个k维的向量,
引入一个简单的参数向量pT,维度为k进行学习,和wide部分一起得到最终的AFM输出。
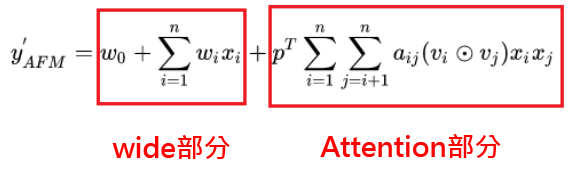
总结AFM的网络结构来说,有如下特点:
- Attention Network
AFM的亮点所在,通过一个attention net生成一个关于特征交叉项的权重,然后将FM原来的二次项直接累加,变成加权累加。本质上是一个加权平均,学习xjxj的交叉特征重要性
- Deep Network
没有deep,卒。
Attention net学习得到的交叉项直接学些个pt参数就输出了,少了DNN部分的表达,对高阶特征部分的进一步学习可能存在瓶颈。
另外,FFM其实也引入了field的概念去学习filed和featrue之间的权重。没有了deep 部分的AFM,和优化的FFM上限应该比较接近。
AFM等价于 FM + embedding + attention + MLP(一层),需要学习的参数有:
(1)FM部分参数:1+n
(2)Embedding部分参数: n*k
(3)Attention Network部分参数: k*t + t*2
(4)MLP部分参数:k*1
9. Deep&Cross Network(DCN)
在ctr预估中,特征交叉是很重要的一步,但目前的网络结构,最多都只学到二级交叉。LR模型采用原始人工交叉特征,FM自动学习xi和xj的二阶交叉特征,
而PNN用product方式做二阶交叉,NFM和AFM也都采用了Bi-interaction的方式学习特征的二阶交叉。对于更高阶的特征交叉,只有让deep去学习了。
为解决这个问题,google在2017年提出了Deep&Cross Network,简称DCN的模型,可以任意组合特征,而且不增加网络参数。图11为DCN的结构。
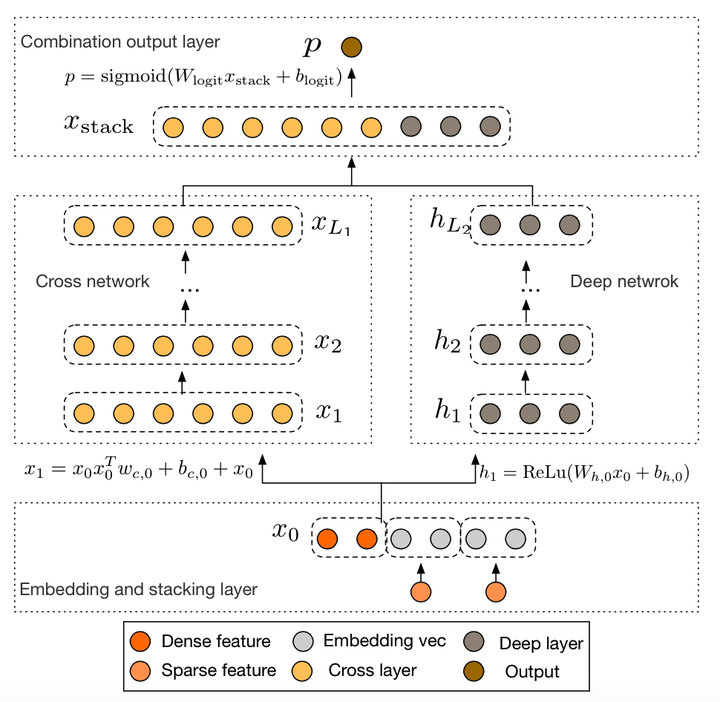
图11 DCN模型结构
整个网络分4部分组成:
(1)Embedding and stacking layer
之所以不把embedding和stacking分开来看,是因为很多时候,embedding和stacking过程是分不开的。
前面讲到的各种 XX-based FM 网络结构,利用FM学到的v向量可以很好的作为embedding。而在很多实际的业务结构,可能已经有了提取到的embedding特征信息,
例如图像的特征embedding,text的特征embedding,item的embedding等,还有其他连续值信息,例如年龄,收入水平等,这些embedding向量stack在一起后,一起作为后续网络结构的输入。
当然,这部分也可以用前面讲到的FM来做embedding。为了和原始论文保持一致,这里我们假设X0向量维度为d(上文的网络结构中为k),这一层的做法就是简答的把各种embedding向量concat起来。
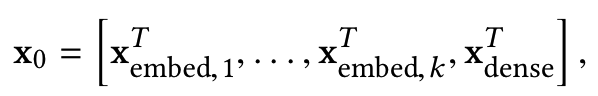
(2)Deep layer netwok
在embedding and stacking layer之后,网络分成了两路,一路是传统的DNN结构。表示如下
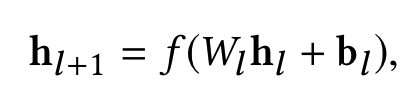
为简化理解,假设每一层网络的参数有m个,一共有Ld层,输入层由于和上一层连接,有d*m个参数(d为x0向量维度),后续的Ld-1层,
每层需要m*(m+1)个参数,所以一共需要学习的参数有 d*m+m*(m+1)*(Ld-1)。最后的输出也是个m维向量Hl2
(3)Cross layer network
Embedding and stacking layer输入后的另一路就是DCN的重点工作了。假设网络有L1层,每一层和前一层的关系可以用如下关系表示
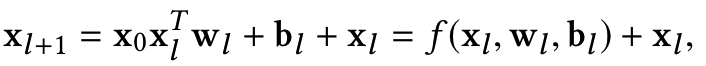
可以看到f是待拟合的函数,xl即为上一层的网络输入。需要学习的参数为wl和bl,因为xl维度为d, 当前层网络输入xl+1也为d维,
待学习的参数wl和bl也都是d维度向量。因此,每一层都有2*d的参数(w和b)需要学习,网络结构如下。
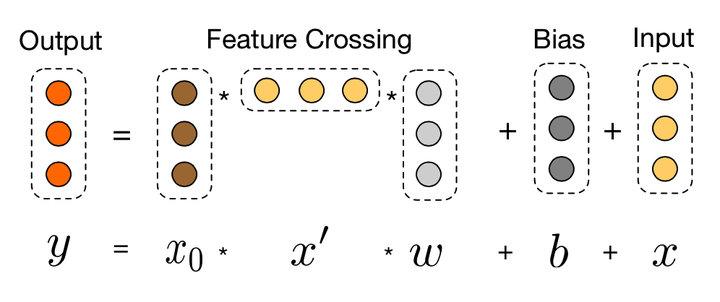
经过Lc层的cross layer network后,在该layer最后一层Lc层的输出为Lc2的d维向量
(4)Combination Output Layer
经过cross network的输出XL1(d维)和deep network之后的向量输入(m维)直接做concat,变为一个d+m的向量,最后套一个LR模型,需要学习参数为1+d+m。
总结起来,DCN引入的cross network理论上可以表达任意高阶组合,同时每一层保留低阶组合,参数的向量化也控制了模型的复杂度。
DCN等价于embedding + cross + deep + LR
(1)embedding部分参数: 根据情况而定
(2)cross部分参数:2*d*Lc(Lc为cross网路层数)
(3)deep部分参数:d*(m+1)+m*(m+1)*(Ld-1) (Ld为深度网络层数,m为每层网络参数)
(4)LR 部分参数:1+d+m
10. Deep Interest Network (DIN)
最后介绍阿里在2017年提出的Deep Interest Network,简称DIN模型。与上面的FNN,PNN等引入低阶代数范式不同,DIN的核心是基于数据的内在特点,引入了更高阶的学习范式。
用户的兴趣是多种多样的,从数学的角度来看,用户的兴趣在兴趣空间是一个多峰分布。在预测ctr时,用户embedding表示的兴趣维度,很多是和当前item是否点击无关的,
只和用户兴趣中的局部信息有关。因此,受attention机制启发,DIN在embedding层后做了一个action unit的操作,对用户的兴趣分布进行学习后再输入到DNN中去,网络结构如图12所示
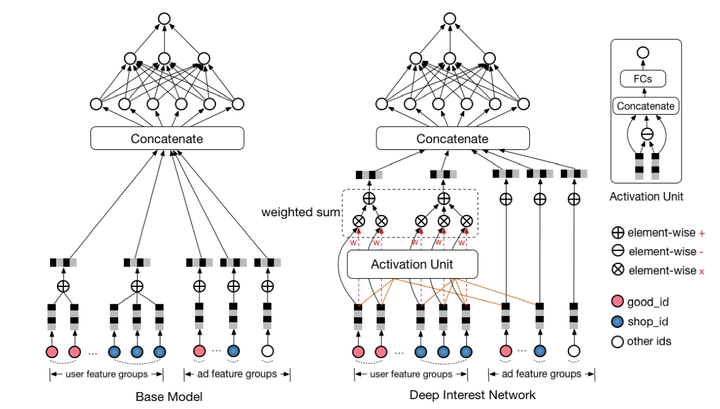
图12 DIN模型结构
DIN把用户特征、用户历史行为特征进行embedding操作,视为对用户兴趣的表示,之后通过attention network,对每个兴趣表示赋予不同的权值。
- Vu:表示用户最终向量
- Vi:表示用户兴趣向量(shop_id, good_id..)
- Va:表示广告表示向量
- Wi: 对于候选广告,attention机制中该兴趣的权重
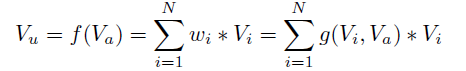
可以看到,对于用户的每个兴趣向量Vi,都会通过学习该兴趣的权重Vi, 来作为最终的用户表示。



