SeqGAN 原理简述

1. 背景
GAN在之前发的文章里已经说过了，虽然现在GAN的变种越来越多，用途广泛，但是它们的对抗思想都是没有变化的。简单来说，就是在生成的过程中加入一个可以鉴别真实数据和生成数据的鉴别器，使生成器G和鉴别器D相互对抗，D的作用是努力地分辨真实数据和生成数据，G的作用是努力改进自己从而生成可以迷惑D的数据。当D无法再分别出真假数据，则认为此时的G已经达到了一个很优的效果。
它的诸多优点是它如今可以这么火爆的原因：
- 可以生成更好的样本
- 模型只用到了反向传播,而不需要马尔科夫链
- 训练时不需要对隐变量做推断
- G的参数更新不是直接来自数据样本,而是使用来自D的反向传播
- 理论上,只要是可微分函数都可以用于构建D和G,因为能够与深度神经网络结合做深度生成式模型

它的最后一条优点也恰恰就是它的局限，在NLP中，数据不像图片处理时是连续的，可以微分，我们在优化生成器的过程中不能找到“中国 + 0.1”这样的东西代表什么，因此对于离散的数据，普通的GAN是无法work的。

2. 大体思路
这位还在读本科的作者想到了使用RL来解决这个问题。

 

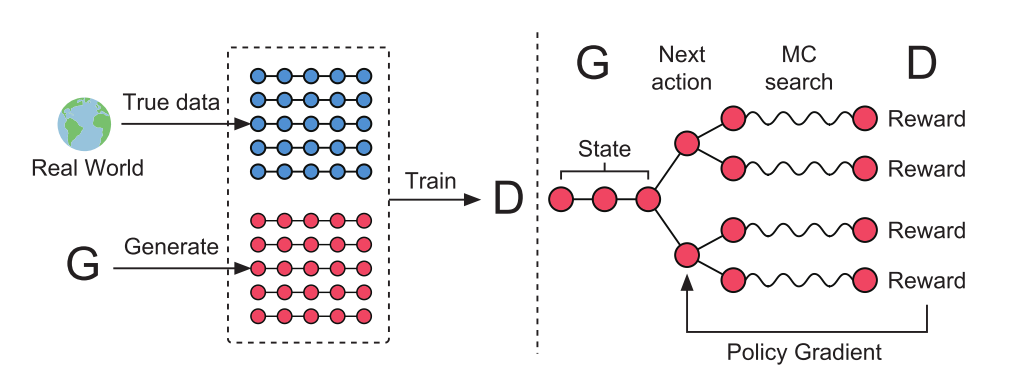
如上图（左）所示，仍然是对抗的思想，真实数据加上G的生成数据来训练D。但是从前边背景章节所述的内容中，我们可以知道G的离散输出，让D很难回传一个梯度用来更新G，因此需要做一些改变，看上图（右），paper中将policy network当做G，已经存在的红色圆点称为现在的状态（state），要生成的下一个红色圆点称作动作（action），因为D需要对一个完整的序列评分，所以就是用MCTS（蒙特卡洛树搜索）将每一个动作的各种可能性补全，D对这些完整的序列产生reward，回传给G，通过增强学习更新G。这样就是用Reinforcement learning的方式，训练出一个可以产生下一个最优的action的生成网络。

3. 主要内容
不论怎么对抗，目的都是为了更好的生成，因此我们可以把生成作为切入点。生成器G的目标是生成sequence来最大化reward的期望。

 

在这里把这个reward的期望叫做J(θ)。就是在s0和θ的条件下，产生某个完全的sequence的reward的期望。其中Gθ()部分可以轻易地看出就是Generator Model。而QDφGθ()（我在这里叫它Q值）在文中被叫做一个sequence的action-value function 。因此，我们可以这样理解这个式子：G生成某一个y1的概率乘以这个y1的Q值，这样求出所有y1的概率乘Q值，再求和，则得到了这个J(θ)，也就是我们生成模型想要最大化的函数。

所以问题来了，这个Q值怎么求？
paper中使用的是REINFORCE algorithm 并且就把这个Q值看作是鉴别器D的返回值。

 

因为不完整的轨迹产生的reward没有实际意义，因此在原有y_1到y_t-1的情况下，产生的y_t的Q值并不能在y_t产生后直接计算，除非y_t就是整个序列的最后一个。paper中想了一个办法，使用蒙特卡洛搜索（就我所知“蒙特卡洛”这四个字可以等同于“随意”）将y_t后的内容进行补全。既然是随意补全就说明会产生多种情况，paper中将同一个y_t后使用蒙特卡洛搜索补全的所有可能的sequence全都计算reward，然后求平均。

 

就这样，我们生成了一些逼真的sequence。我们就要用如下方式训练D。

 

这个式子很容易理解，最大化D判断真实数据为真加上D判断生成数据为假，也就是最小化它们的相反数。

D训练了一轮或者多轮（因为GAN的训练一直是个难题，找好G和D的训练轮数比例是关键）之后，就得到了一个更优秀的D，此时要用D去更新G。G的更新可以看做是梯度下降。

 

其中，

 

αh代表学习率。

以上就是大概的seqGAN的原理。

4. 算法

首先随机初始化G网络和D网络参数。

通过MLE预训练G网络，目的是提高G网络的搜索效率。

使用预训练的G生成一些数据，用来通过最小化交叉熵来预训练D。

开始生成sequence，并使用方程（4）计算reward（这个reward来自于G生成的sequence与D产生的Q值）。

使用方程（8）更新G的参数。

更优的G生成更好的sequence，和真实数据一起通过方程（5）训练D。

以上1，2，3循环训练直到收敛。

5. 实验
论文的实验部分就不是本文的重点了，有兴趣的话看一下paper就可以了。

---------------------

原文：https://blog.csdn.net/yinruiyang94/article/details/77675586

另一篇不错的文章：https://blog.csdn.net/Mr_tyting/article/details/80269143