DeepHyperX代码理解-HamidaEtAl
代码复现自论文《3-D Deep Learning Approach for Remote Sensing Image Classification》
先对部分基础知识做一些整理:
一、局部连接与参数共享(都减少了参数计算量)
局部连接:基于图像局部相关的原理,保留了图像局部结构,同时减少了网络的权值个数,加快了学习速率,同时也在一定程度上减少了过拟合的可能。
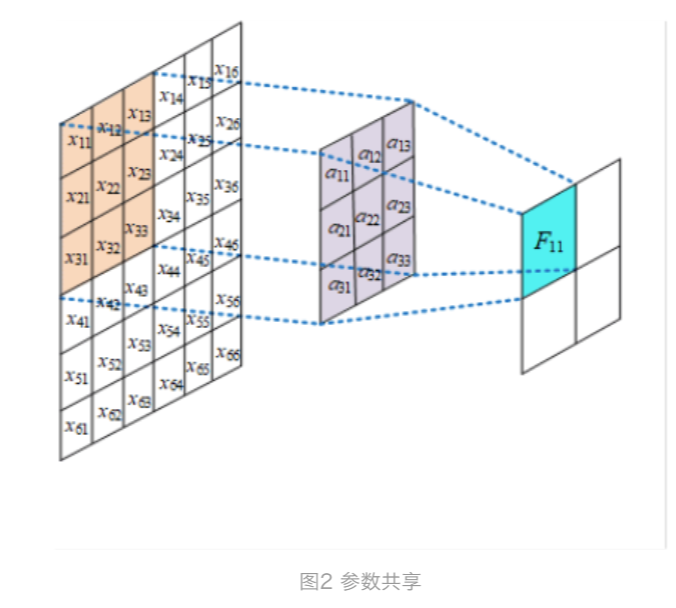
参数共享:下面用图例解释参数共享与不共享的区别。
如图是一个3*3大小的卷积核在进行特征提取,channel=1, 在每个位置进行特征提取的时候都是共享一个卷积核,假设有k个channel,则参数
总量为3*3*k,注意不同channel的参数是不能共享的。
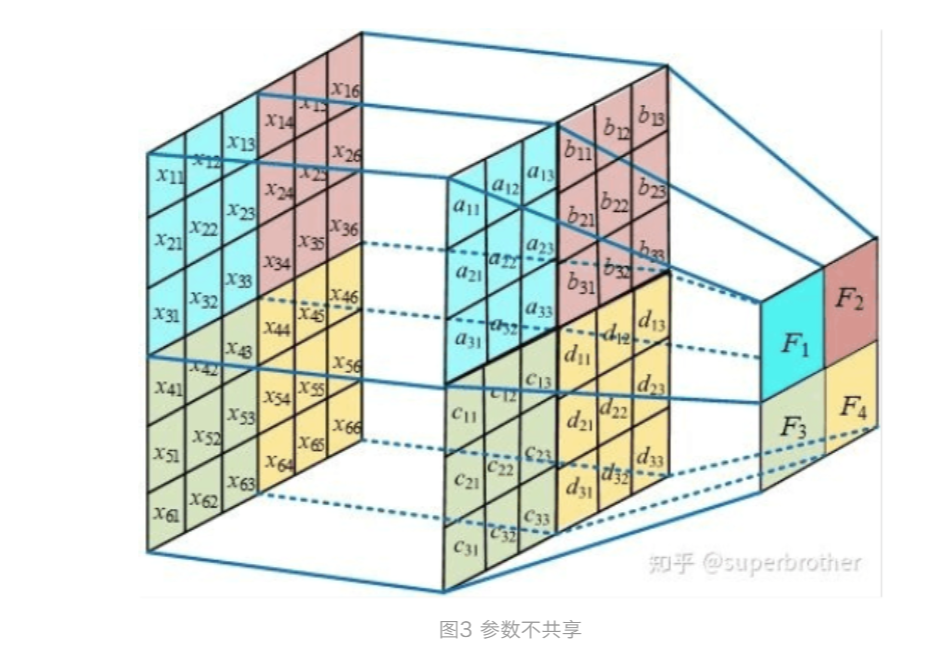
假设现在不使用参数共享,则卷积核作用于矩阵上的每一个位置时其参数都是不一样的,则卷积核的参数数量就与像素矩阵的大小保持一致了,假
设有k个channel,则参数数量为weight*height*k,这对于尺寸较大的图片来说明显是不可取的。
二、多通道输入输出:
首先理解fliter与kernel区别:kernel是fliter的组成成分,一个fliter就会对应生成一个特征图。
下图为多通道输入,单通道输出。有一个fliter,一个fliter包括三个kernel,最后生成一个特征图(一个fliter就对应一个特征图)
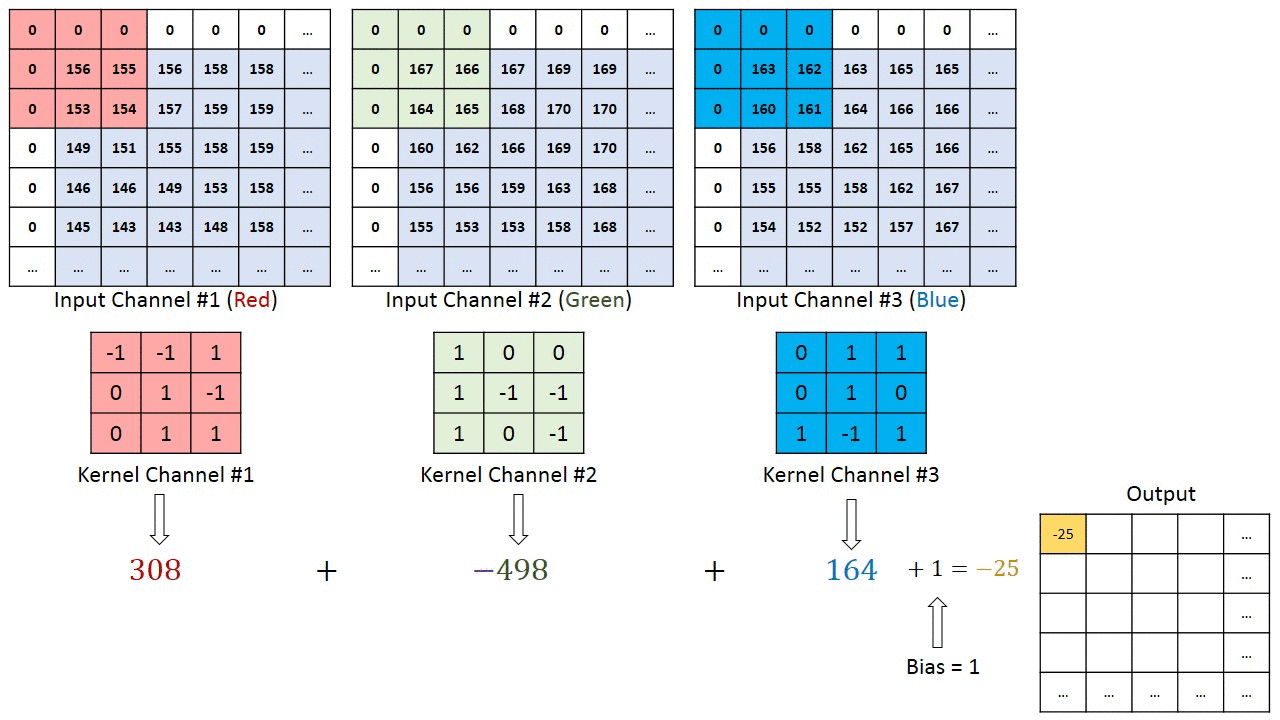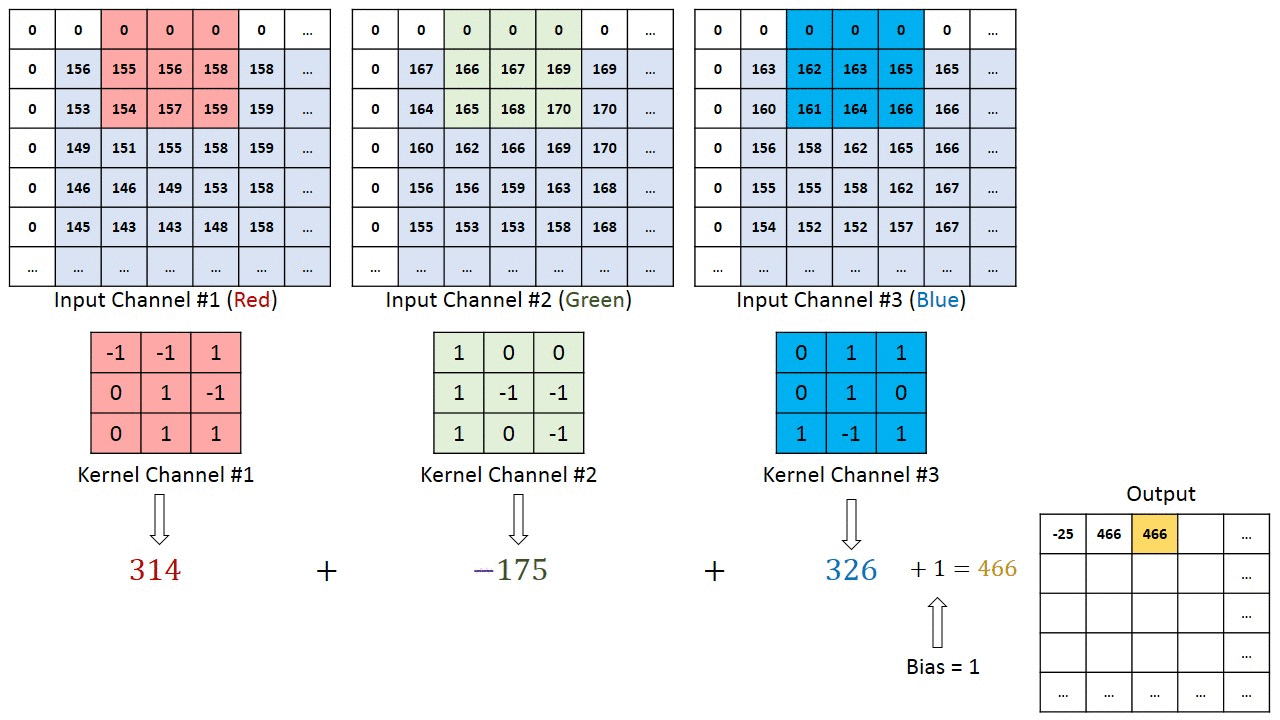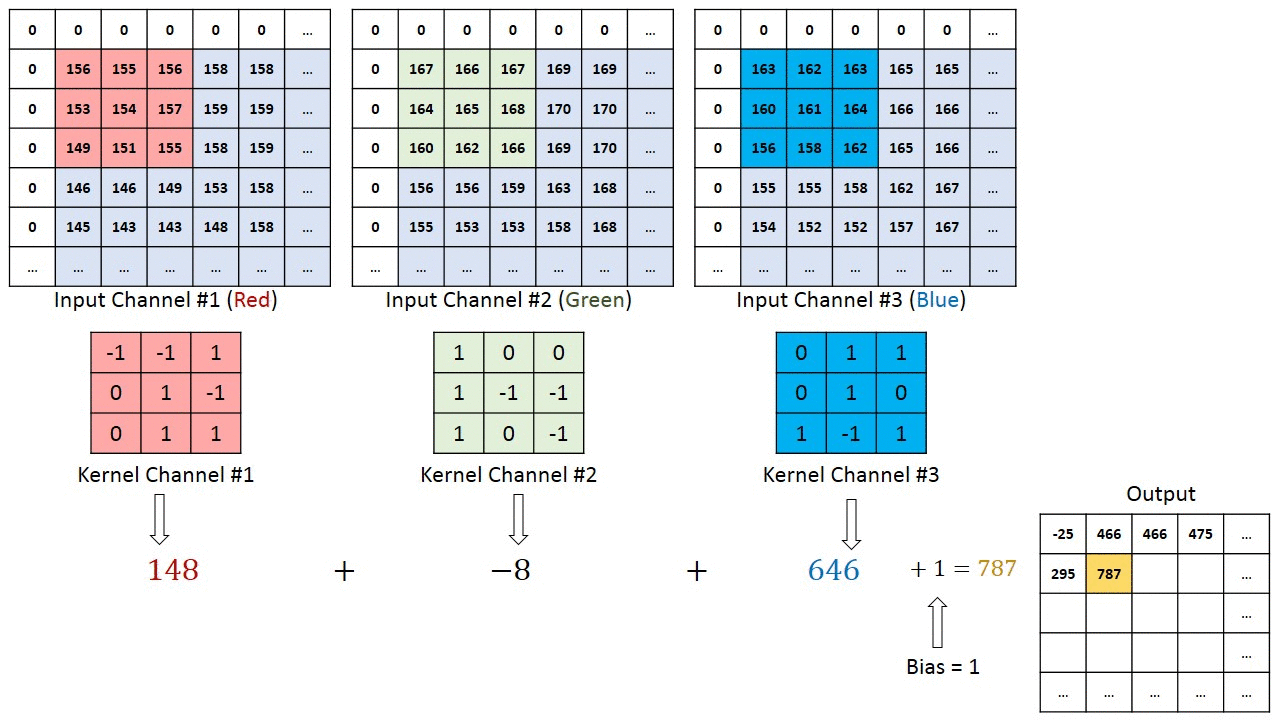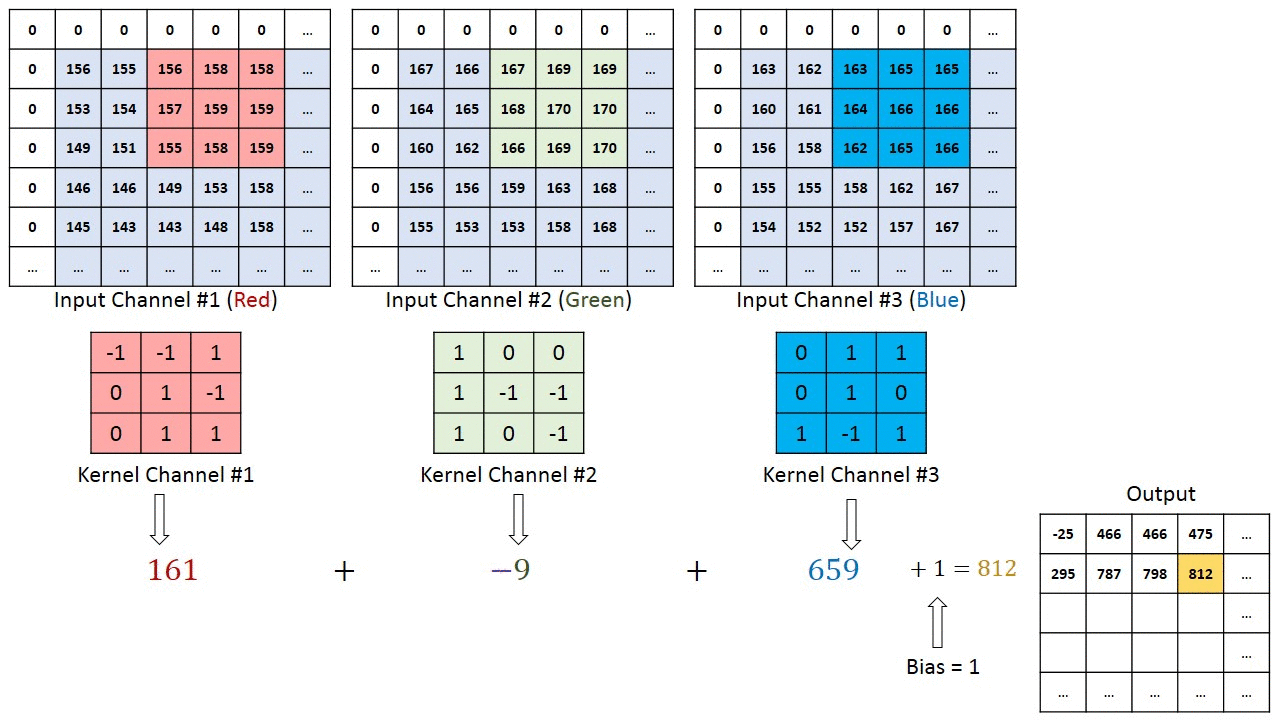
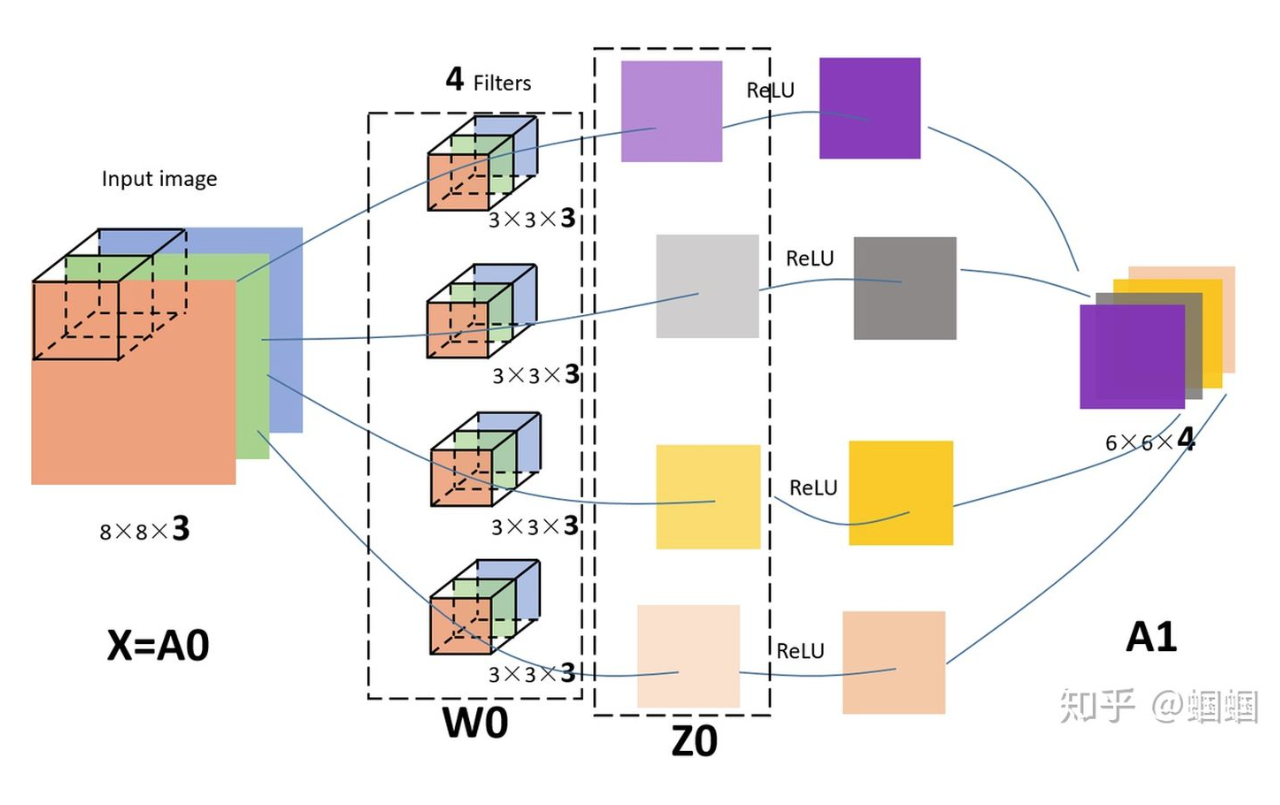
下图为直观展示,输入为8*8*3的RGB三通道图片,设置了4个fliter对应四个输出通道,也就是输出4个特征图。每个fliter有3个kernel。
三、2D卷积代码示例:
1 import torch as t 2 import torch.nn as nn 3 4 class A(nn.Module): 5 def __init__(self): 6 super(A, self).__init__() 7 #三个2D卷积层结构,每个卷积层的输入和输出通道数均为2,卷积核和大小是(3, 3) 8 #torch.nn.Conv2d(in_channels, out_channels, kernel_size, stride=1, 9 #padding=0, dilation=1, groups=1, bias=True, 10 #padding_mode='zeros', device=None, dtype=None) 11 self.conv1 = nn.Conv2d(2, 2, kernel_size=(3, 3)) 12 self.conv2 = nn.Conv2d(2, 2, kernel_size=(3, 3)) 13 self.conv3 = nn.Conv2d(2, 2, kernel_size=(3, 3)) 14 15 a = A() 16 print(list(a.parameters()))
运行结果:
1 [Parameter containing: 2 tensor([[[[ 0.0213, -0.2054, 0.0985], 3 [ 0.1254, 0.1202, -0.1115], 4 [-0.0280, 0.0256, 0.1975]], 5 6 [[-0.2118, -0.1683, 0.0056], 7 [-0.0554, 0.2255, -0.1548], 8 [ 0.1747, 0.0449, 0.1606]]], 9 10 11 [[[-0.1328, -0.1700, -0.1048], 12 [ 0.0911, -0.2230, 0.0685], 13 [ 0.0886, 0.1765, -0.1879]], 14 15 [[-0.0581, 0.1266, -0.1030], 16 [-0.0170, 0.0387, -0.0641], 17 [-0.0127, -0.2099, -0.2213]]]], requires_grad=True), Parameter containing: 18 tensor([ 0.0877, -0.1969], requires_grad=True), Parameter containing: 19 tensor([[[[-0.0266, 0.1511, -0.0034], 20 [-0.1070, -0.1734, -0.1017], 21 [ 0.0053, 0.1358, -0.0542]], 22 23 [[-0.0436, 0.1587, -0.0375], 24 [ 0.0125, -0.0431, -0.0877], 25 [-0.0766, 0.0405, -0.1306]]], 26 27 28 [[[-0.1449, -0.0315, -0.0236], 29 [ 0.0118, 0.2230, -0.2137], 30 [-0.1108, -0.1178, 0.0027]], 31 32 [[ 0.2184, 0.1964, -0.0959], 33 [-0.0385, -0.0523, 0.2135], 34 [-0.0387, 0.1951, -0.1546]]]], requires_grad=True), Parameter containing: 35 tensor([-0.0942, -0.2029], requires_grad=True), Parameter containing: 36 tensor([[[[ 8.9598e-02, -3.3190e-02, 1.0606e-01], 37 [-2.2397e-02, 2.0944e-01, -6.8180e-02], 38 [-1.7312e-01, 2.2318e-01, 1.9368e-01]], 39 40 [[ 7.0529e-02, -2.0741e-01, -1.2648e-01], 41 [-1.7503e-01, 1.7972e-01, -1.0417e-01], 42 [-1.9124e-01, -4.2022e-02, 1.4635e-01]]], 43 44 45 [[[-8.0857e-02, 8.5098e-03, 7.0629e-02], 46 [ 1.6926e-01, -1.7654e-02, -9.3033e-02], 47 [-2.9836e-02, -2.2935e-01, 1.1450e-01]], 48 49 [[ 1.3848e-01, -5.7713e-02, 1.5293e-04], 50 [-6.3998e-03, -1.0745e-01, 2.8835e-03], 51 [-1.7894e-01, 2.2133e-01, 5.2435e-02]]]], requires_grad=True), Parameter containing: 52 tensor([-0.1026, 0.0207], requires_grad=True)]
上面代码是定义的一个2D卷积网络架构,有3个卷积层,每个卷积层的输入通道和输出通道(对应fliter为2)都为2,每个fliter中有两个3*3的kernel(对应两个输入通道)。代码中的两个1*2的向量为bias。
四、3D卷积的示意图和示例代码:
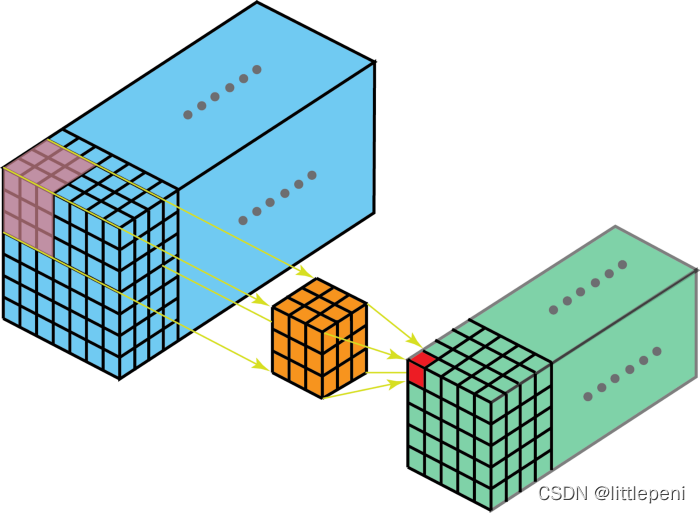
1 class B(nn.Module): 2 def __init__(self): 3 super(B, self).__init__() 4 self.conv1 = nn.Conv3d( 5 1, # 输入图像的channel数,C_in 6 3, # 卷积产生的channel数,C_out 7 kernel_size=2, # 卷积核的尺寸,这里实际是(2,2,2),第一维表示卷积核处理的帧数 8 stride=(1,1,1), # 卷积步长,(D,H,W) 9 padding=(0,0,0), # 输入的每一条边补充0的层数,(D,H,W) 10 bias=False) 11 self.conv2 = nn.Conv3d(1, 3, kernel_size=(2, 2, 2), stride=(1, 1, 1), padding=(0, 0, 0), bias=False) 12 13 b = B() 14 print(list(b.parameters()))
运行结果:
1 [Parameter containing: 2 tensor([[[[[-0.0895, -0.1651], 3 [-0.1319, 0.2510]], 4 5 [[-0.1616, -0.2614], 6 [ 0.0383, 0.2656]]]], 7 8 9 10 [[[[-0.0809, -0.1821], 11 [-0.0624, -0.1401]], 12 13 [[-0.3170, 0.1499], 14 [-0.3449, 0.2639]]]], 15 16 17 18 [[[[ 0.2779, -0.0731], 19 [ 0.0439, -0.0353]], 20 21 [[ 0.2853, -0.3177], 22 [ 0.0559, -0.3290]]]]], requires_grad=True), Parameter containing: 23 tensor([[[[[-0.2529, -0.0537], 24 [ 0.0955, -0.1513]], 25 26 [[ 0.0310, 0.2558], 27 [-0.1903, -0.1561]]]], 28 29 30 31 [[[[-0.2919, -0.3142], 32 [ 0.0190, -0.1089]], 33 34 [[-0.0586, 0.1541], 35 [-0.2402, -0.3339]]]], 36 37 38 39 [[[[-0.3260, -0.0500], 40 [ 0.1392, 0.1486]], 41 42 [[ 0.1664, 0.1514], 43 [ 0.0345, -0.1979]]]]], requires_grad=True)]
三维数据输入通道为1,输出通道为3,那么fliter数为3,每个fliter中有1个kernel(2,2,2),因为两个3D-Conv参数一样,所以每个3D-Conv有3个(2,2,2)的tensor。这里如果对应到高光谱数据集,输入通道也为1。因为整个高光谱数据集就是一个3维的volume,整个数据集图像由长*宽*光谱维组成。
论文复现:
原论文网络结构:
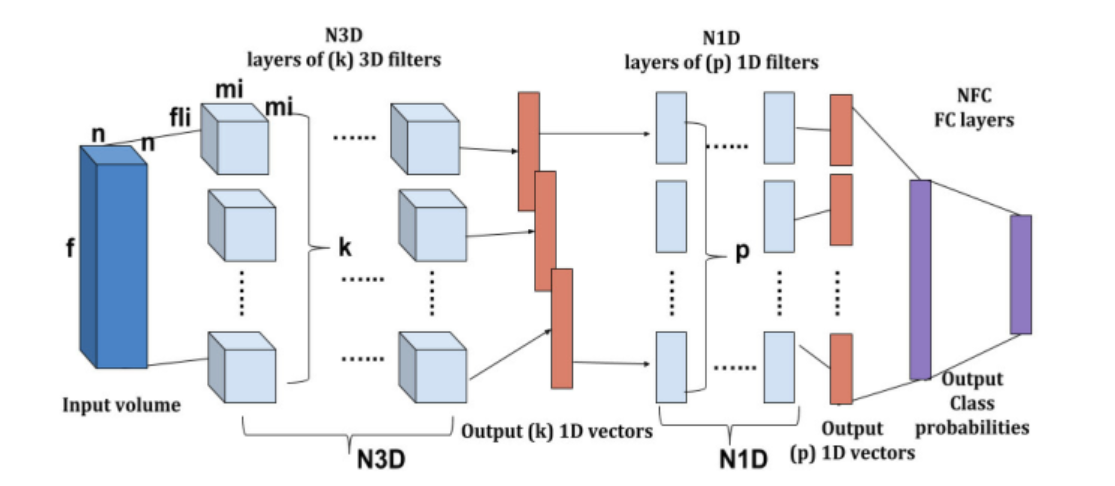
复现网络:
输入维度:Image has dimensions 610x340 and 103 channels
网络结构及参数:
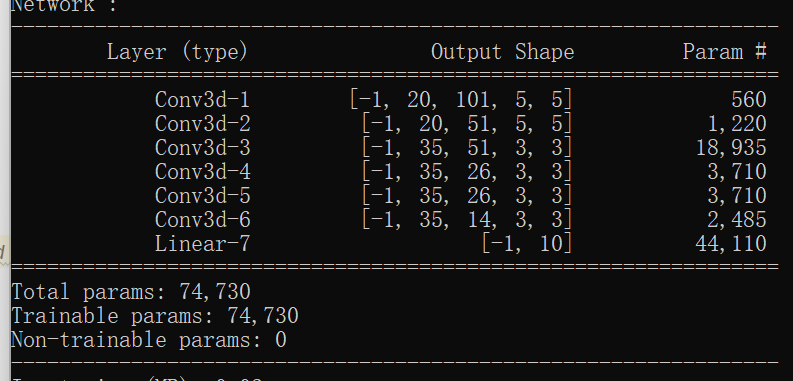
复现代码:
1 elif name == "hamida": 2 patch_size = kwargs.setdefault("patch_size", 5) 3 center_pixel = True 4 model = HamidaEtAl(n_bands, n_classes, patch_size=patch_size) 5 lr = kwargs.setdefault("learning_rate", 0.01) 6 optimizer = optim.SGD(model.parameters(), lr=lr, weight_decay=0.0005) 7 kwargs.setdefault("batch_size", 100) 8 criterion = nn.CrossEntropyLoss(weight=kwargs["weights"])
1 class HamidaEtAl(nn.Module): 2 """ 3 3-D Deep Learning Approach for Remote Sensing Image Classification 4 Amina Ben Hamida, Alexandre Benoit, Patrick Lambert, Chokri Ben Amar 5 IEEE TGRS, 2018 6 https://ieeexplore.ieee.org/stamp/stamp.jsp?arnumber=8344565 7 """ 8 9 @staticmethod 10 def weight_init(m):#权重初始化 11 if isinstance(m, nn.Linear) or isinstance(m, nn.Conv3d): 12 init.kaiming_normal_(m.weight) #kaiming_normal_均匀初始化方法 13 init.zeros_(m.bias) 14 15 def __init__(self, input_channels, n_classes, patch_size=5, dilation=1): 16 super(HamidaEtAl, self).__init__() 17 # The first layer is a (3,3,3) kernel sized Conv characterized 18 # by a stride equal to 1 and number of neurons equal to 20 19 self.patch_size = patch_size#每次截取图像patch大小(5,5) 20 self.input_channels = input_channels#输入通道数(波段数) 21 dilation = (dilation, 1, 1) 22 23 if patch_size == 3: 24 self.conv1 = nn.Conv3d( 25 1, 20, (3, 3, 3), stride=(1, 1, 1), dilation=dilation, padding=1 26 ) 27 else: 28 self.conv1 = nn.Conv3d( 29 1, 20, (3, 3, 3), stride=(1, 1, 1), dilation=dilation, padding=0 30 ) 31 # Next pooling is applied using a layer identical to the previous one 32 # with the difference of a 1D kernel size (1,1,3) and a larger stride 33 # equal to 2 in order to reduce the spectral dimension 34 #为什么要用卷积层要替代池化层: 35 # 使用2×2的最大池化,与使用卷积(stride为2)来做down sample性能并没有明显差别, 36 # 而且使用卷积(stride为2)相比卷积(步进为1)+池化,还可以减少卷积运算量和一个池化层。何乐而不为呢。 37 self.pool1 = nn.Conv3d( 38 20, 20, (3, 1, 1), dilation=dilation, stride=(2, 1, 1), padding=(1, 0, 0) 39 ) 40 # Then, a duplicate of the first and second layers is created with 41 # 35 hidden neurons per layer. 42 self.conv2 = nn.Conv3d( 43 20, 35, (3, 3, 3), dilation=dilation, stride=(1, 1, 1), padding=(1, 0, 0) 44 ) 45 self.pool2 = nn.Conv3d( 46 35, 35, (3, 1, 1), dilation=dilation, stride=(2, 1, 1), padding=(1, 0, 0) 47 ) 48 # Finally, the 1D spatial dimension is progressively reduced 49 # thanks to the use of two Conv layers, 35 neurons each, 50 # with respective kernel sizes of (1,1,3) and (1,1,2) and strides 51 # respectively equal to (1,1,1) and (1,1,2) 52 self.conv3 = nn.Conv3d( 53 35, 35, (3, 1, 1), dilation=dilation, stride=(1, 1, 1), padding=(1, 0, 0) 54 ) 55 self.conv4 = nn.Conv3d( 56 35, 35, (2, 1, 1), dilation=dilation, stride=(2, 1, 1), padding=(1, 0, 0) 57 ) 58 59 # self.dropout = nn.Dropout(p=0.5) 60 61 self.features_size = self._get_final_flattened_size() 62 # The architecture ends with a fully connected layer where the number 63 # of neurons is equal to the number of input classes. 64 self.fc = nn.Linear(self.features_size, n_classes) 65 66 self.apply(self.weight_init) 67 68 def _get_final_flattened_size(self):#计算fc前的输出tensor大小,用随机的X去测试得到,这样就不用自己去推到了 69 with torch.no_grad(): 70 x = torch.zeros( 71 (1, 1, self.input_channels, self.patch_size, self.patch_size) 72 ) 73 x = self.pool1(self.conv1(x)) 74 x = self.pool2(self.conv2(x)) 75 x = self.conv3(x) 76 x = self.conv4(x) 77 _, t, c, w, h = x.size() 78 return t * c * w * h 79 80 def forward(self, x): 81 x = F.relu(self.conv1(x)) 82 x = self.pool1(x) 83 x = F.relu(self.conv2(x)) 84 x = self.pool2(x) 85 x = F.relu(self.conv3(x)) 86 x = F.relu(self.conv4(x)) 87 x = x.view(-1, self.features_size)#对tensor resize相当于做展平(flatten)操作 88 # x = self.dropout(x) 89 x = self.fc(x) 90 return x
关于参数dilation的解释:https://blog.csdn.net/qimo601/article/details/112624091
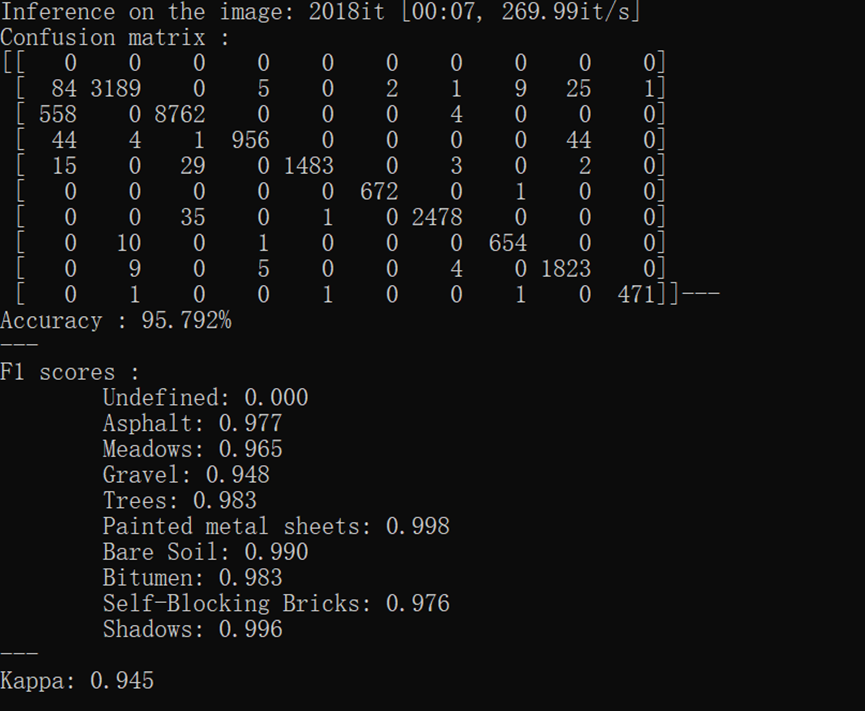
运行结果:
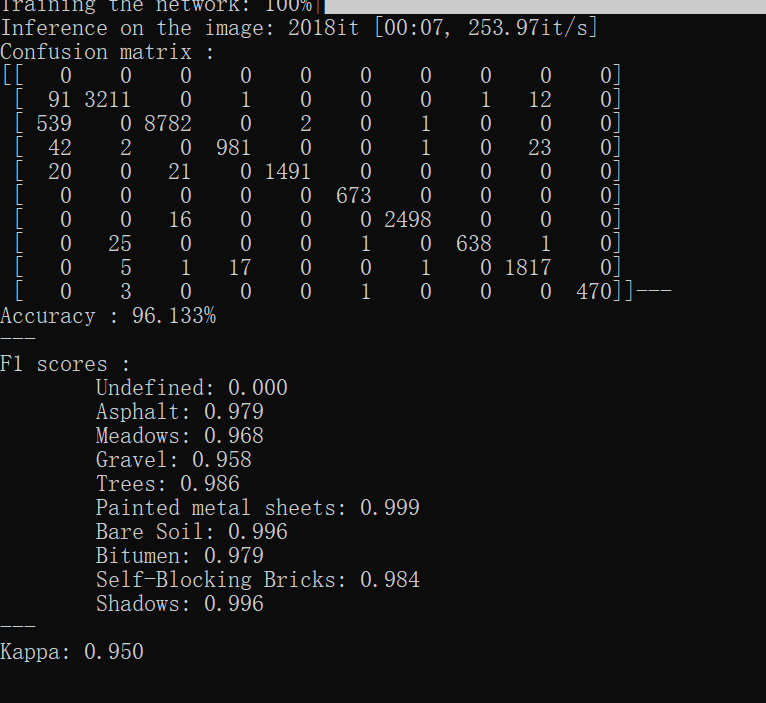
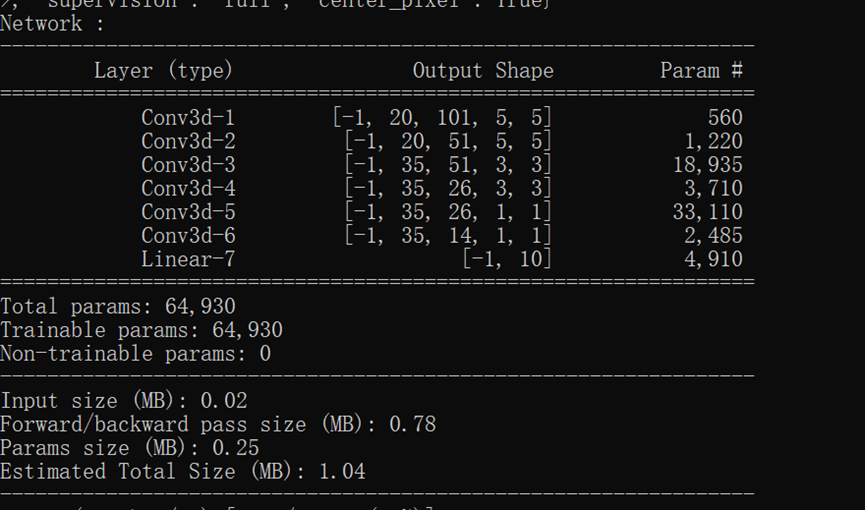
通过阅读代码发现和原论文中的结构并不完全相同,试着去修改了一层网络参数去接近原网络结构:
self.conv3 = nn.Conv3d( 35, 35, (3, 1, 1), dilation=dilation, stride=(1, 1, 1), padding=(1, 0, 0) ) ->> self.conv3 = nn.Conv3d( 35, 35, (3, 3, 3), dilation=dilation, stride=(1, 1, 1), padding=(1, 0, 0) )
但发现最终效果不如上面结果,可能是对原论文提出的结构稍作改进了吧。
参考资料:
https://github.com/nshaud/DeepHyperX
https://blog.csdn.net/weixin_38481963/article/details/109906338
https://blog.csdn.net/abbcdc/article/details/123332063
https://wenku.baidu.com/view/fa899796f221dd36a32d7375a417866fb84ac087.html



 浙公网安备 33010602011771号
浙公网安备 33010602011771号