线性代数——C语言实现（超长篇慎入）【存在问题，不建议看】

线性代数

镇楼图

Pixiv: csyday

仅作为学习线代的实验，不会特别注重内存泄漏、bug等问题

目前不打算用写稀疏矩阵，之后可能会转C++

〇、准备工作（构建分数ADT）

点击查看详细内容

要知道网上很多在线计算最烦的一点是没有分数全都是小数，这样答案也写不进作业中。

为了方便学习~~写作业~~，这里特地写一块内容

typedef struct __fraction{
	int numerator;//分子
    int denominator;//分母
}fraction,*Fraction;

bool fraction_ifexist(Fraction a){
	//作用：判断分数是否是有效的 
    //如果分母为0则返回0视为无效
    //如果分母不为0则返回1视为有效
	return (a->denominator == 0) ? false : true;
};

int fraction_ifproper(Fraction a){
	//作用：判断分数是否为真分数 
	//如果分数是真分数则返回1否则返回0 
	if(!fraction_ifexist(a)){
		printf("错误：分母为0！！！");
		exit(-1);
	}
	return (a->denominator > a->numerator) ? true : false;
};

int gcd(int a,int b){
	//求最大公约数 
	b = abs(b);
	a = abs(a);
	if(b > a){
		int t = a;
		a = b;
		b = t;
	}
	return (b == 0) ? a : gcd(b,a%b);
}

void fraction_simplify(Fraction a){
	//作用：约分
	if(!fraction_ifexist(a)){
		printf("错误：分母为0！！！");
		exit(-1);
	}
	int GCD = gcd(a->numerator,a->denominator);
	a->numerator /= GCD;
	a->denominator /= GCD;
	if(a->denominator < 0){
		a->numerator *= -1;
		a->denominator *= -1;
	}
	return;
}

int lcm(int a,int b){
	//求最小公倍数 
	return abs(a)*abs(b)/gcd(a,b);
}

void fraction_complicated(Fraction a,Fraction b){
	//作用：通分
	if(!fraction_ifexist(a) || !fraction_ifexist(b)){
		printf("错误：分母为0！！！");
		exit(-1);
	}
	int LCM = lcm(a->denominator,b->denominator);
	a->numerator *= LCM/a->denominator;
	b->numerator *= LCM/b->denominator;
	a->denominator = b->denominator = LCM;
	return;
}

Fraction fraction_add(Fraction a,Fraction b){
	//作用：加法 
	if(!fraction_ifexist(a) || !fraction_ifexist(b)){
		printf("错误：分母为0！！！");
		exit(-1);
	}
	Fraction r = (Fraction)malloc(sizeof(fraction));
	fraction_complicated(a,b);
	r->numerator = a->numerator + b->numerator;
	r->denominator = a->denominator;
	fraction_simplify(r);
	return r;
}

Fraction fraction_sub(Fraction a,Fraction b){
	//作用：减法 
	if(!fraction_ifexist(a) || !fraction_ifexist(b)){
		printf("错误：分母为0！！！");
		exit(-1);
	}
	Fraction r = (Fraction)malloc(sizeof(fraction));
	fraction_complicated(a,b);
	r->numerator = a->numerator - b->numerator;
	r->denominator = a->denominator;
	fraction_simplify(r);
	return r;
}

Fraction fraction_mul(Fraction a,Fraction b){
	//作用：乘法
	 if(!fraction_ifexist(a) || !fraction_ifexist(b)){
		printf("错误：分母为0！！！");
		exit(-1);
	}
	Fraction r = (Fraction)malloc(sizeof(fraction));
	r->numerator = a->numerator * b->numerator;
	r->denominator = a->denominator * b->denominator;
	fraction_simplify(r);
	return r;
}

Fraction fraction_div(Fraction a,Fraction b){
	//作用：除法 
	 if(!fraction_ifexist(a) || !fraction_ifexist(b)){
		printf("错误：分母为0！！！");
		exit(-1);
	}
	Fraction r = (Fraction)malloc(sizeof(fraction));
	r->numerator = a->numerator * b->denominator;
	r->denominator = a->denominator * b->numerator;
	fraction_simplify(r);
	return r;
}

void fraction_print(Fraction a){
	//作用：约分并输出
	 if(!fraction_ifexist(a)){
		printf("错误：分母为0！！！");
		exit(-1);
	}
	fraction_simplify(a);
	if(a->denominator == 1 || a->numerator == 0){
		a->denominator = 1;
		printf("%d",a->numerator);
	}else printf("%d/%d",a->numerator,a->denominator); 
	return;
}

fraction fraction_create(int a,int b){
	//生成一个以a为分子b为分母的分数
    fraction r;
    r.numerator = a;
    r.denominator = b;
    return r;
}

这样就完成了准备工作

一、线性方程(组)

点击查看详细内容

线性方程

$a_1x_1+a_2x_2...+a_nx_n=b$

其中$a_i$为系数，$x_i$为变量，$b$为值

$a_i$和$b$可以为实数或复数

解

得出的一组可行的变量值组合为解

解分为三种情况

无解不存在组合使得线性方程(组)成立	有限解只有有限个组合使得线性方程(组)成立	无穷解有无数种组合使得线性方程(组)成立

解构成的集合称为解集

有解的线性方程(组)称为是相容的

无解的线性方程(组)称为是不相容的

线性方程组

所谓线性方程组是一组线性方程构成的一组变量有关联的方程组

比如

$\begin{cases}&x&+&y&+&z=&50 \\ &5x&+&2y&+&z=&100 \end{cases}$

增广矩阵

可以将变量、运算符去掉，只保留系数、值

这样由线性方程组用矩阵符号化后的矩阵称为'增广矩阵'

$\begin{bmatrix}1&1&1&50 \\ 5&2&1&100 \end{bmatrix}$

这个矩阵中$\begin{bmatrix}1&1&1&50\end{bmatrix}$称为行

这个矩阵中$\begin{bmatrix}1 \\ 50\end{bmatrix}$称为列

维数是指矩阵所包含的行数和列数

typedef struct __matrix{
	Fraction **base;//矩阵首元素
    int row;//矩阵行数
    int col;//矩阵列数
}matrix,*Matrix;

void matrix_null(Matrix a,int m,int n){
	//创建m×n的零矩阵
	a->base = (Fraction**)malloc(sizeof(Fraction*)*m);
	for(int i = 0;i < m;i++)
		a->base[i] = (Fraction*)malloc(sizeof(Fraction)*n);
    //二维数组赋予内存稍麻烦
	a->row = m;
	a->col = n;
	for(int i=0;i < a->row;i++)
		for(int j=0;j < a->col;j++)
			a->base[i][j] = fraction_create(0,1);
    return;
}

void matrix_edelete(matrix a,int i,int j){
    //释放矩阵内a(i,j)的内存
    free(a.base[i][j]);
    return;
}

void matrix_set(matrix a,int i,int j,Fraction value){
	//将矩阵a的第i、j位置的元素修改为value 
	matrix_edelete(a,i,j);
	a.base[i][j] = value;
	return;	
}

void matrix_print(matrix a){
    //输出矩阵
	for(int i = 0;i < a.row;i++){
		for(int j = 0;j < a.col;j++){
			fraction_print(a.base[i][j]);
			printf("\t");
		}
		printf("\n");
	}
}

void matrix_delete(matrix a){
	//删除矩阵 
	for(int i = 0;i < a.row;i++){
		free(a.base[i]);
	}
	free(a.base);
	a.base = NULL;
	a.col = a.row = 0;
	return;
}

matrix matrix_rowcombine(matrix a,matrix b){
	//作用：按行合并矩阵a,b
	if(a.row != b.row){
		printf("错误：行数不一致");
		exit(-1);
	}
	matrix new;
	matrix_null(&new,a.row,a.col+b.col);
	for(int i = 0;i < a.row;i++){
		for(int j = 0;j < a.col;j++){
			matrix_set(new,i,j,a.base[i][j]);
		}
	}
	for(int i = 0;i < a.row;i++){
		for(int j = a.col;j < a.col+b.col;j++){
			matrix_set(new,i,j,b.base[i][j - a.col]);
		}
	}
	return new;
}

matrix matrix_colcombine(matrix a,matrix b){
	//作用：按列合并矩阵a,b
	if(a.col != b.col){
		printf("错误：列数不一致");
		exit(-1);
	}
	matrix new;
	matrix_null(&new,a.row+b.row,a.col);
	for(int i = 0;i < a.row;i++){
		for(int j = 0;j < a.col;j++){
			matrix_set(new,i,j,a.base[i][j]);
		}
	}
	for(int i = a.row;i < a.row+b.row;i++){
		for(int j = 0;j < a.col;j++){
			matrix_set(new,i,j,b.base[i - a.row][j]);
		}
	}
	return new;
}

void matrix_identity(Matrix a,int n){
    //生成n阶的单位矩阵
    a->base = (Fraction**)malloc(sizeof(Fraction*)*n);
	for(int i = 0;i < n;i++)
		a->base[i] = (Fraction*)malloc(sizeof(Fraction)*n);
	a->row = n;
	a->col = n;
	for(int i=0;i < a->row;i++)
		for(int j=0;j < a->col;j++)
			if(i != j) a->base[i][j] = fraction_create(0,1);
			else a->base[i][j] = fraction_create(1,1);
	return;
}

void matrix_square(Matrix a,int n){
    //生成n阶的单位矩阵
    a->base = (Fraction**)malloc(sizeof(Fraction*)*n);
	for(int i = 0;i < n;i++)
		a->base[i] = (Fraction*)malloc(sizeof(Fraction)*n);
	a->row = n;
	a->col = n;
	for(int i=0;i < a->row;i++)
		for(int j=0;j < a->col;j++)
			a->base[i][j] = fraction_create(0,1);
	return;
}

现在就能用几行代码来生成一个矩阵了，更加具体的操作我会随着线代的学习来写代码

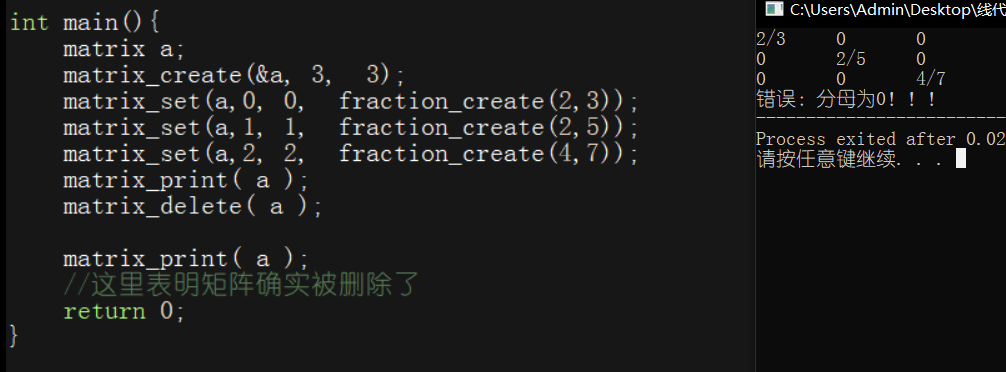
初等变换

增广矩阵不过是符号化后的线性方程组，线性方程组该怎么求还就怎么求

根据原本对线性方程组的求解方法，在增广矩阵里可以抽象为一种规律

使用下述规律后这个增广矩阵依然等价

①倍加：可以将某一行/列加上另一行的某个倍数

②对换：可以任意交换两行/列

③倍乘：某一行/列可以乘上某一不为0的倍数

初等变换也是可逆的

bool matrix_ifrow(matrix a,int i){
	//判断第i行是否在a矩阵里合法 
	return (i >=0 && i < a.row) ? true : false;
}

①对换

void matrix_transfrom_rreplace(matrix a,int i1,int i2){
	//矩阵a进行初等行变换，i1行与i2行交换 
	if(!matrix_ifrow(a,i1) || !matrix_ifrow(a,i2)){
		printf("错误：所描述的行已超出行数");
		exit(-1);
	} 
	for(int j = 0;j < a.col;j++){
		Fraction t = a.base[i1][j];
		a.base[i1][j] = a.base[i2][j];
		a.base[i2][j] = t;
	}
	return;
}

②倍乘

void matrix_transfrom_rmul(matrix a,int i,Fraction c){
	//矩阵a进行初等行变换，i1行乘上某已分数 
	if(!matrix_ifrow(a,i)){
		printf("错误：所描述的行已超出行数");
		exit(-1);
	} 
	for(int j = 0;j < a.col;j++){
		a.base[i][j] = fraction_mul(a.base[i][j],c);
	}
	return;
}

③加法

void matrix_transfrom_radd(matrix a,int i1,int i2){
	//矩阵a进行初等行变换，i1行加i2行
	if(!matrix_ifrow(a,i1) || !matrix_ifrow(a,i2)){
		printf("错误：所描述的行已超出行数");
		exit(-1);
	} 
	for(int j = 0;j < a.col;j++){
		a.base[i1][j] = fraction_add(a.base[i1][j],a.base[i2][j]);
	}
	return;
}

④倍加

void matrix_transfrom_rcadd(matrix a,int i1,Fraction c,int i2){
	//矩阵a进行初等行变换，i1行加c的倍i2行
	if(!matrix_ifrow(a,i1) || !matrix_ifrow(a,i2)){
		printf("错误：所描述的行已超出行数");
		exit(-1);
	} 
	for(int j = 0;j < a.col;j++){
		a.base[i1][j] = fraction_add(a.base[i1][j],fraction_mul(a.base[i2][j],c));
	}
	return;
}

行阶梯形矩阵

以下面这个矩阵为例

$\begin{bmatrix}0&1&2&3&0&15 \\ 0&0&5&6&7&16 \\ 0&0&0&0&9&17 \\ 0&0&0&0&0&0 \end{bmatrix}$

其中矩阵当中如果有某一行元素全部为0就称这是零行

在非零行的最左侧的元素称为先导元素，这里是1,5,9

主元除了满足先导元素条件以外，还要保证左侧全是0

主元所在位置称为主元位置，主元所在列称为主元列

所谓主元就算在主元位置上的非零元素

为了符号化的表示，用■表示先导元素，*表示由先导元素所形成的阶梯内的元素，其他元素为0的则省略不写

此例符号化表示为

$\begin{bmatrix}&■&*&*&*&* \\ &&■&*&*&* \\ &&&&■&* \\ &&&&& \end{bmatrix}$

行阶梯形矩阵

只有满足以下条件才能算得上是行阶梯矩阵

①非零行要在零行上

②先导元素一定是从左到右依次排列好的

③先导元素所在列的下方元素都为0

简化阶梯形矩阵(U)

这是增广矩阵的最简形式，简单到能一眼看出解，这是比其他行阶梯形矩阵还要好算的形式

除了行阶梯形矩阵的定义以外还要满足以下条件

①先导元素为1

②先导元素是这一列唯一的非零元素

每个矩阵只有唯一的简化阶梯形矩阵(简化阶梯形的唯一性)

程序里常用rref或ref来表示（英文缩写）

二、高斯消元法（行化简算法）

点击查看详细内容

为了计算求解线性方程组需要求解增广矩阵的阶梯形矩阵或简化阶梯形矩阵

高斯消元算法正是汇编了一套方法来求解，而其原理也很简单就是行初等变换

①构建框架

目前接触到了$row~<=~col$的情况，$row~>~col$的情况干脆忽略了

void matrix_augmented_REF(matrix a){
    //求解矩阵等价的阶梯形矩阵
	if(a.row > a.col){
		printf("无法处理：行数大于列数\n");
		exit(-1);
	}
	//
}

②选择主元

在求解线性方程组一般情况会将主元优先选择在$(0,0)$的位置，但也有特殊情况

■$(0,0)$恰好是零元素

这种情况好解决，可以通过交换其他不是零元素的行，在程序里默认找绝对值的最大值

■$(0,0)$这一列都是零元素，交换了也没用

这种情况的话，都是0，不存在所谓的主元，这一列都不用考虑了，需要移动到下1列找主元

//分数操作9
int fraction_abscmp(Fraction a,Fraction b){
	/*作用：比较分数a与b绝对值的大小
      若a < b返回-1
	  若a = b返回0
	  若a > b返回1*/
    fraction_complicated(a,b);
    if(fabs(a->numerator) < fabs(b->numerator))return -1;
    else if(fabs(a->numerator) == fabs(b->numerator))return 0;
    else return 1;
}

bool matrix_augmented_REF_select(matrix a,int* posx,int* posy){
     int maxx = *posx;
    //maxx为a.base[maxx][posy]的绝对值最大的横坐标
	for(int i = *posx;i < a.row;i++){
		if(fraction_abscmp(a.base[maxx][*posy],a.base[i][*posy]) < 0)maxx = i;
	}
	//从posy列中索引，找到最大的一个来避免第一种特殊情况
    if(a.base[maxx][*posy]->numerator == 0){
        return false;
    }
    matrix_transfrom_rreplace(a,*posx,maxx);
    return true;
    //然后判断第二种特殊情况，如果成立则换到下一列
    //不然就直接交换来完成第一步操作
    //返回true表示在(posx,posy)这一列成功找到主元
    //返回false表示未找到主元
}

②消元

根据第一步操作，如果未找到主元，则要修改主元位置来重新选择主元，这里先考虑如果找到了主元的情况

//分数操作10
Fraction fraction_opposite(Fraction a){
	//求分数的相反数 
	fraction b;
	b.numerator = -1;
	b.denominator = 1;
	return fraction_mul(a,&b);
}

void matrix_augmented_REF_eliminate(matrix a,int* posx,int* posy){
	//消元
	for(int i = *posx+1;i < a.row;i++){
		matrix_transfrom_rcadd(a,i,fraction_div(a.base[i][*posy],fraction_opposite(a.base[*posx][*posy])),*posx);
    }
    return;
}

③迭代

根据前两步的处理，判断下一个主元位置在哪

■首先要根据第一步不同的返回值来操作

如果返回了true就代表当前列存在主元，位置$(posx,posy)$将移动到$(posx+1,posy+1)$

如果返回了false，位置$(posx,posy)$将移动到$(posx,posy+1)$

■同时需要设置什么时候退出迭代

根据这个算法可知只有要选择主元的位置超出矩阵范围时就不需要再执行了

bool matrix_augmented_REF_iterator(matrix a,bool ifsuccess,int* posx,int* posy){
    (ifsuccess == true) ? (*posx)++,(*posy)++ : (*posy)++ ;
    if(*posx >= a.row || *posy >= a.col-1)return false;
	else return true;
    //修改主元位置
}

④汇总

根据前三步已经描述出了这个算法的流程，接下来只要设置好即可

void matrix_augmented_REF(matrix a){
    //求解矩阵等价的阶梯形矩阵
	if(a.row > a.col){
		printf("无法处理：行数大于列数\n");
		exit(-1);
	}
	int posx = 0,posy = 0;
    bool flag;
	do{
        bool issuccess = matrix_augmented_REF_select(a,&posx,&posy);
        if(issuccess)matrix_augmented_REF_eliminate(a,&posx,&posy);
        flag =  matrix_augmented_REF_iterator(a,issuccess,&posx,&posy);
    }while(flag);
    return;
}

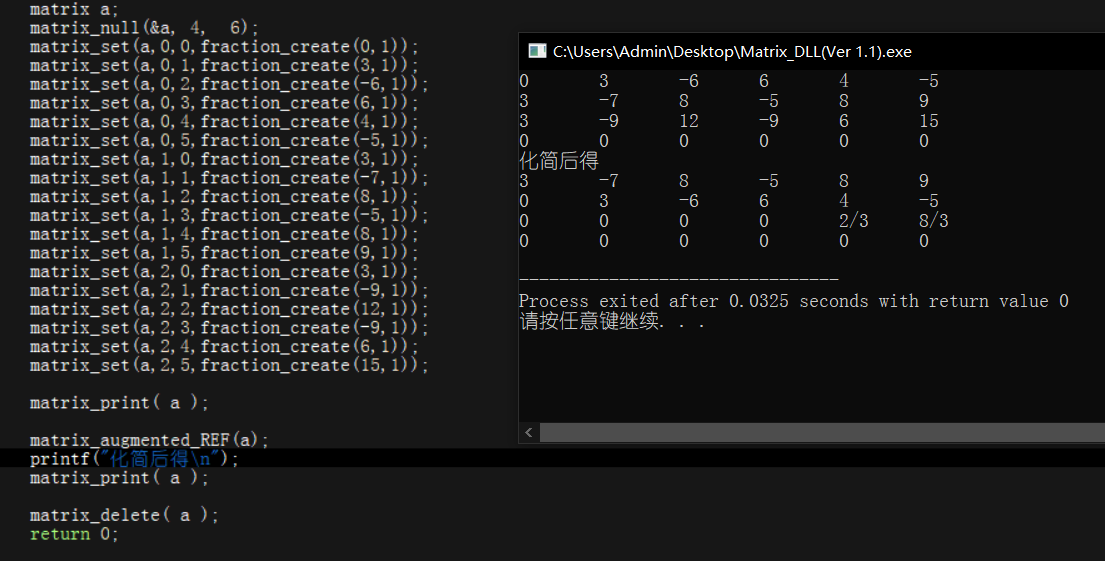
⑤阶梯形矩阵变简化阶梯形矩阵

这里只需要修改之前的一部分代码即可，之前是求得了阶梯形矩阵，只要在求得阶梯形矩阵中加入一些操作就能变成简化阶梯形矩阵

■在消元后额外添加一步——当前主元变为1，并消除主元列中除主元以外其他的元素

void matrix_augmented_REFF_extra(matrix a,int* posx,int* posy){
    matrix_transfrom_rmul(a,*posx,fraction_create(a.base[*posx][*posy]->denominator,a.base[*posx][*posy]->numerator));
    for(int i = (*posx)-1;i >= 0;i--){
    	matrix_transfrom_rcadd(a,i,fraction_opposite(a.base[i][*posy]),*posx);
	}
}

void matrix_augmented_REFF(matrix a){
    //求解矩阵等价的简化阶梯形矩阵 
	if(a.row > a.col){
		printf("无法处理：行数大于列数\n");
		exit(-1);
	}
	int posx = 0,posy = 0;
    bool flag;
	do{
        bool issuccess = matrix_augmented_REF_select(a,&posx,&posy);
        if(issuccess){
			matrix_augmented_REF_eliminate(a,&posx,&posy);
			matrix_augmented_REFF_extra(a,&posx,&posy);
            //这是额外的一步
		}
        flag =  matrix_augmented_REF_iterator(a,issuccess,&posx,&posy);
    }while(flag);
    return;
}

至此完成了求解简化阶梯形矩阵的算法，简化阶梯形矩阵只是在求阶梯形矩阵时多了一步而已

三、线性方程组的解

点击查看详细内容

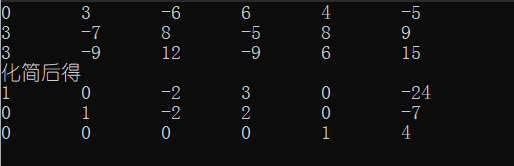
以上面的例子为例，最终通过高斯消元算法求得了简化阶梯形矩阵，主元所对应的变量当作未知量，其余变量当作已知量得

$\begin{cases} x_1=-24+2x_3-3x_4 \\ x_2=-7+2x_3-2x_4 \\x_5=4 \end{cases}$

其中主元所对应的变量称为基本变量，其他不是主元所对应的变量称为自由变量

此例$x_3$、$x_4$是自由变量，其他是基本变量

一般情况是以基本变量当作未知量，自由变量当作已知量

这样求得的解称为通解，而$x_3$、$x_4$取什么是无所谓的

因为含有自由变量，所以有无数种解

存在与唯一性定理

若某一行不存在这种形式$\begin{bmatrix}0& ... &0&b \end{bmatrix}~~~b≠0$，则增广矩阵一定相容

增广矩阵相容时，若增广矩阵不存在自由变量则只有唯一解，若增广矩阵存在自由变量则有无穷多解

之前用set函数来输入代码量实在多，下述代码主要改善一下输入功能

void matrix_input(matrix a,int* n,int* d){
	//n数组元素作为分子，d数组元素作为分母，按行输入
    int count = 0;
    for(int i = 0;i < a.row;i++){
    	for(int j = 0;j < a.col;j++){
    		matrix_set(a,i,j,fraction_create(n[count],d[count]));
    		count++;
		}
	}
	return;
}

void matrix_inputint(matrix a,int* n){
	//n数组元素作为分子，分母为1，按行输入 
    int count = 0;
    for(int i = 0;i < a.row;i++){
    	for(int j = 0;j < a.col;j++){
    		matrix_set(a,i,j,fraction_create(n[count],1));
    		count++;
		}
	}
	return;
}

四、线性变换

点击查看详细内容

这属于线代在图形学应用方面，但这个应用实在重要，直接在此说明了注：这里仅考虑二维的线性变换

$Ax=b$中

$A$代表的是一组基向量构建的新坐标系

$x$代表的是点的位置

$b$代表的是在原坐标系下于新坐标系的点的位置

但换个角度想，$x$如果是表示原坐标系和新坐标系的点

点会存在一个变换

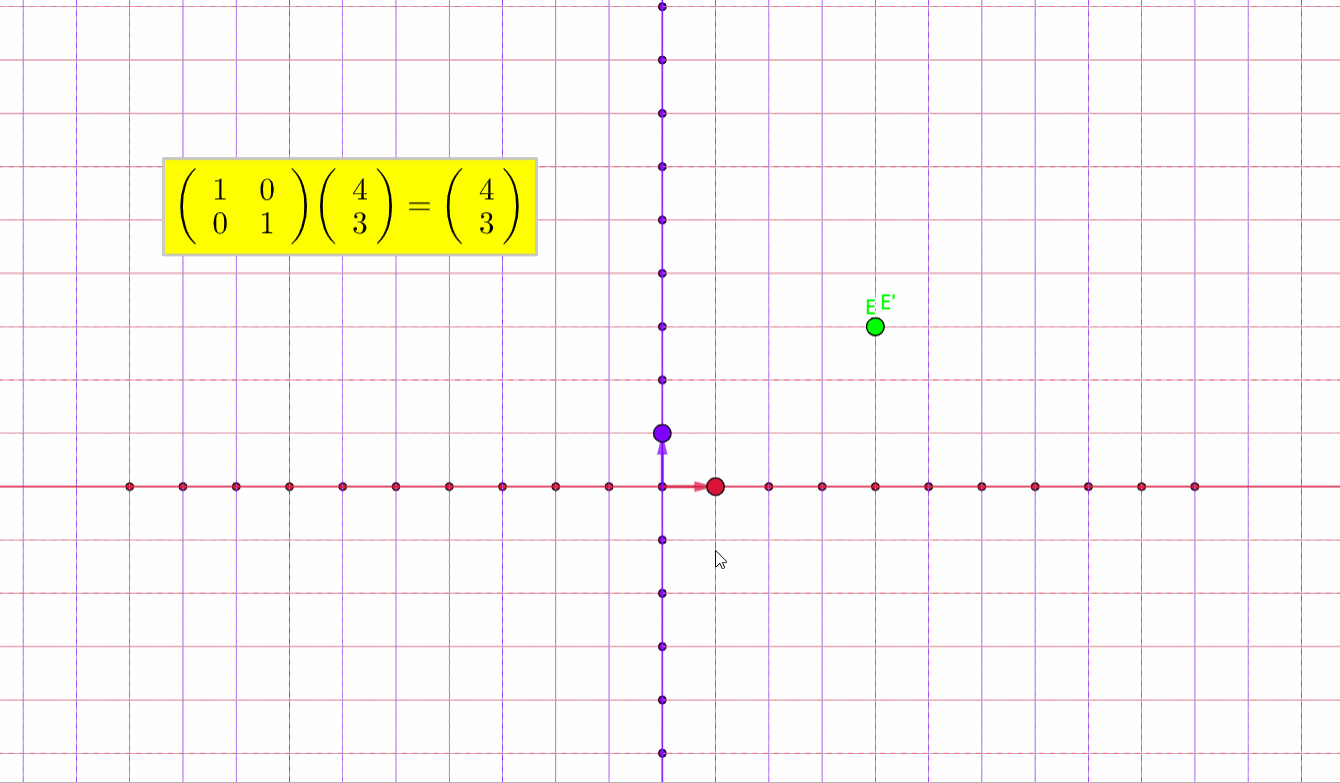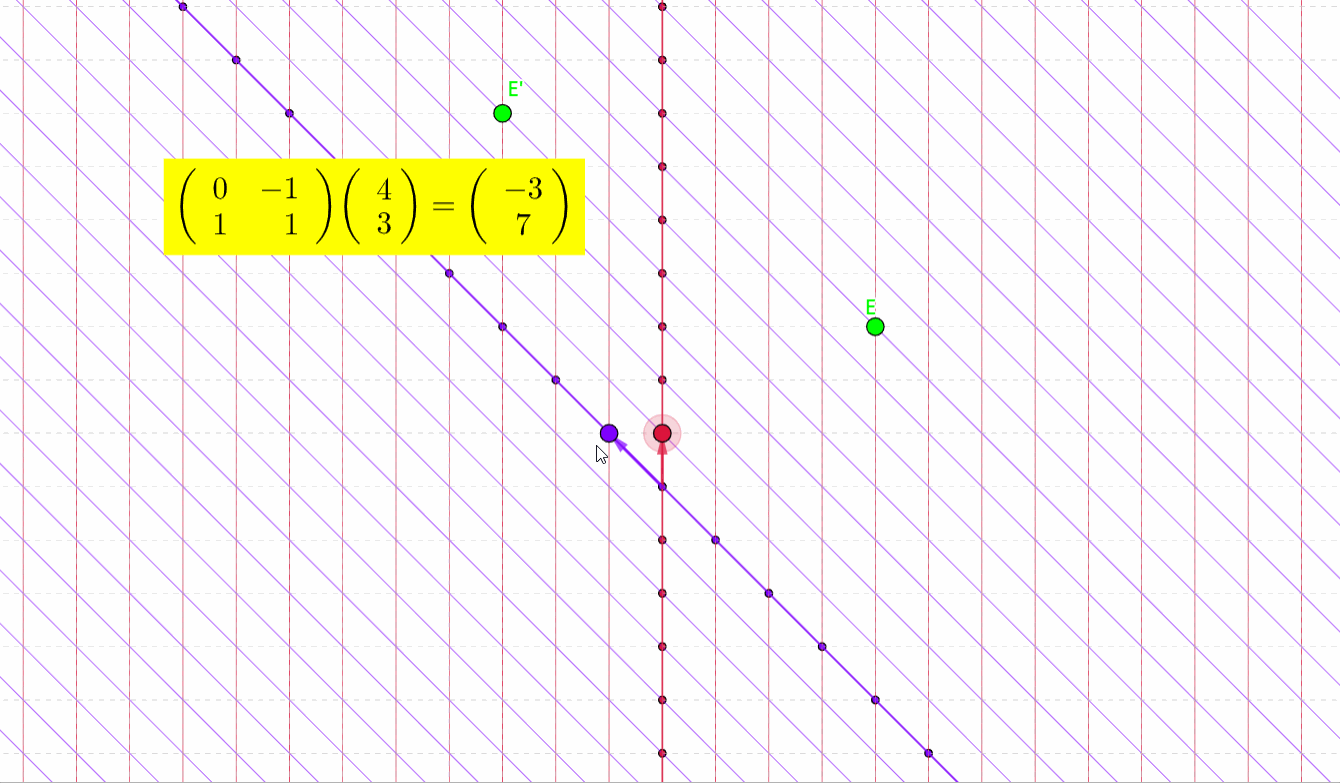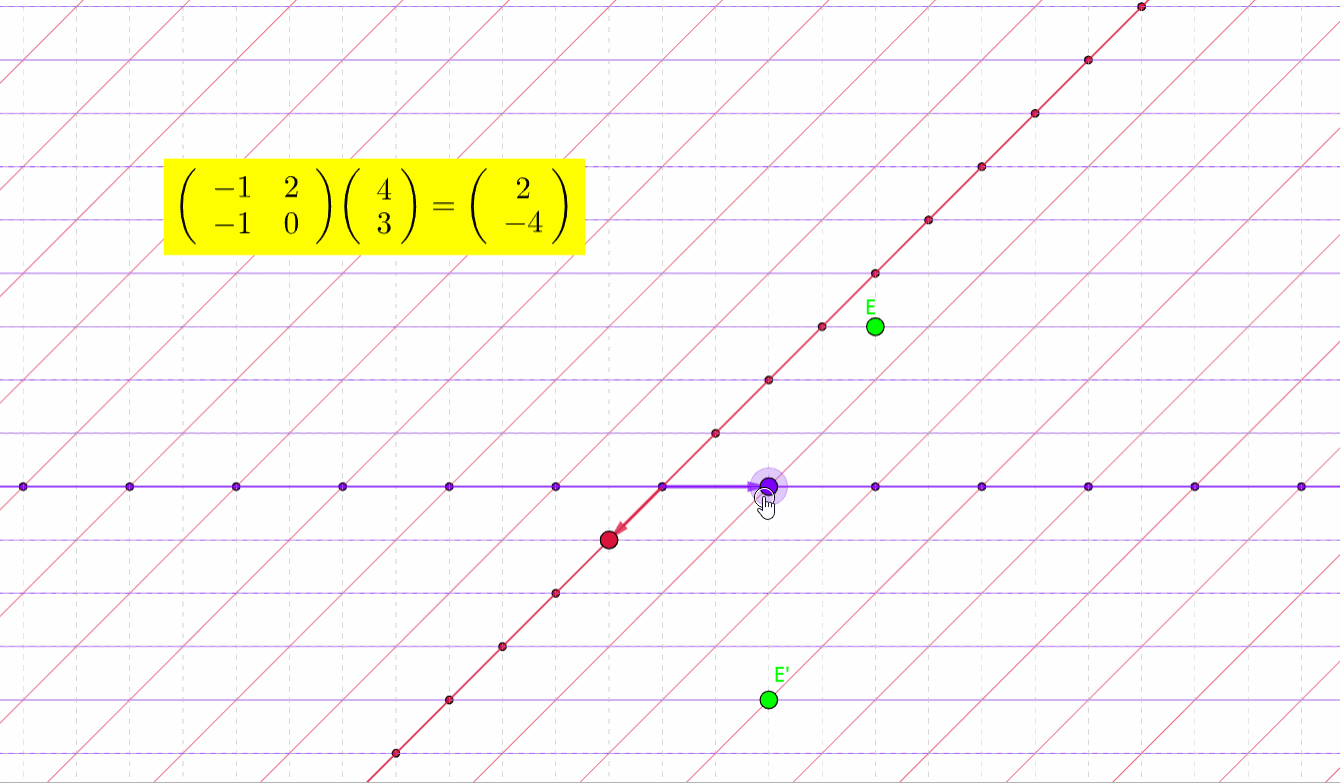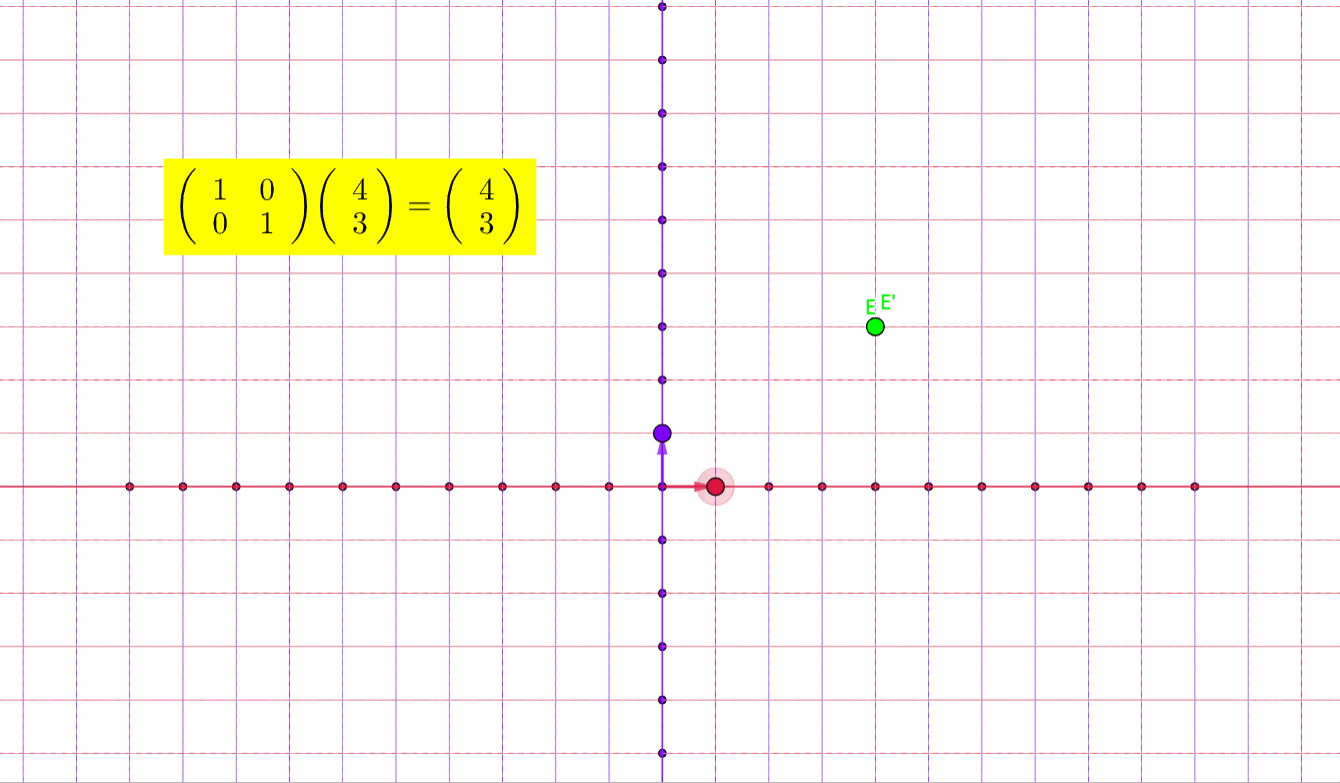
如图所示，E通过矩阵乘法变换到了其他位置

而如果是一个图形，同样会存在一个变换

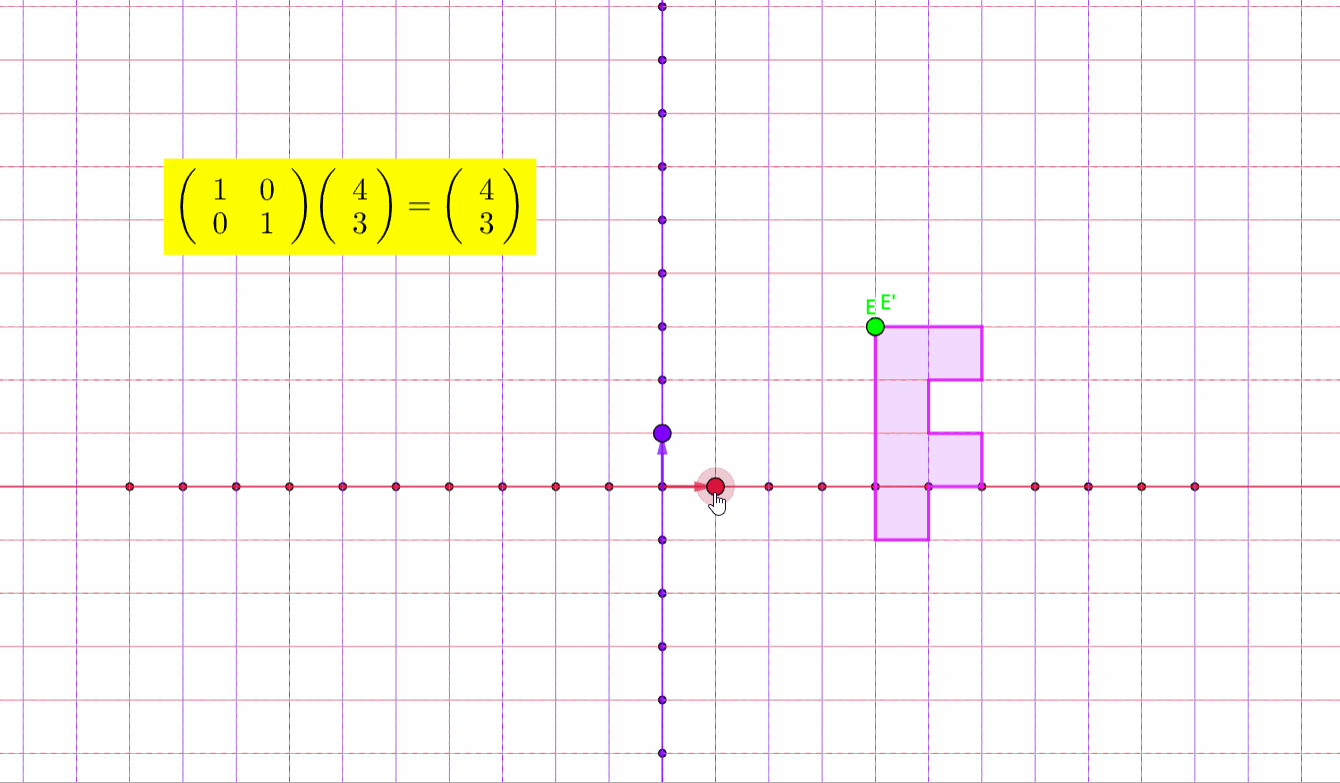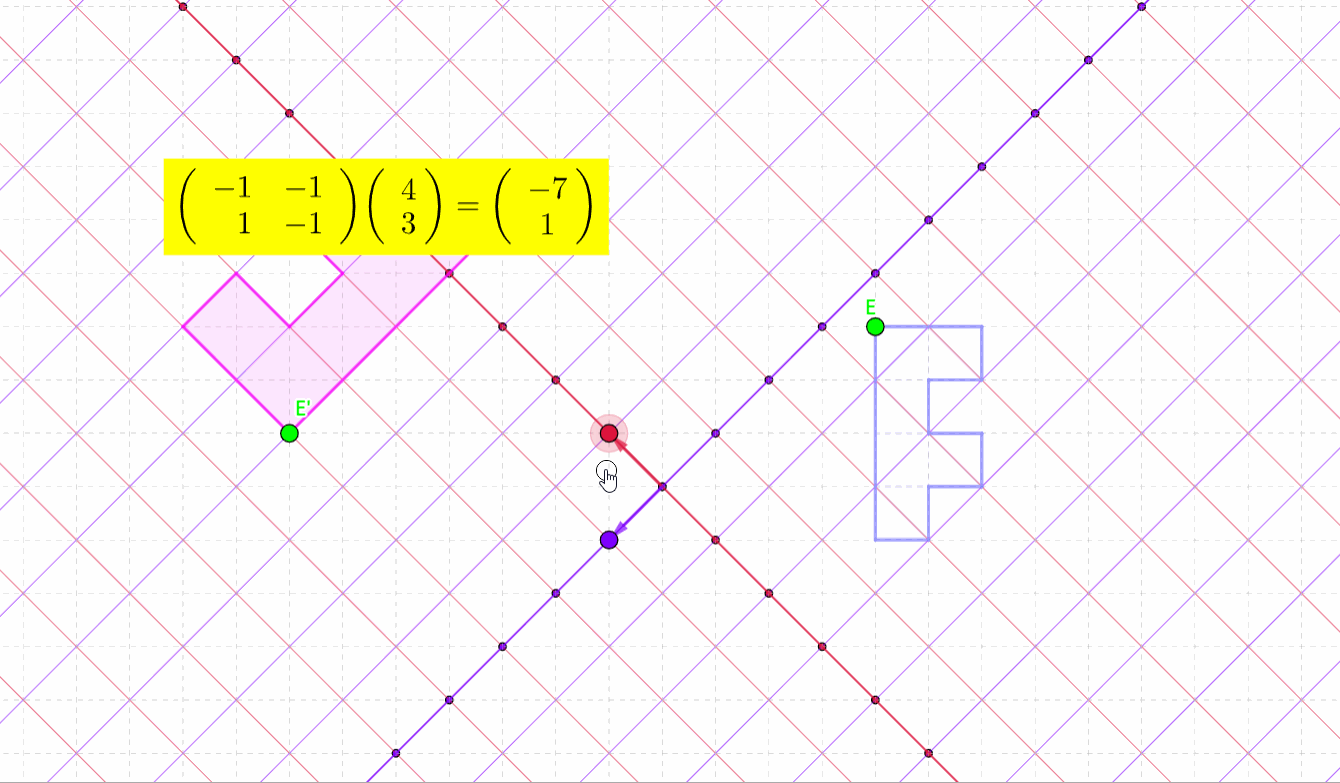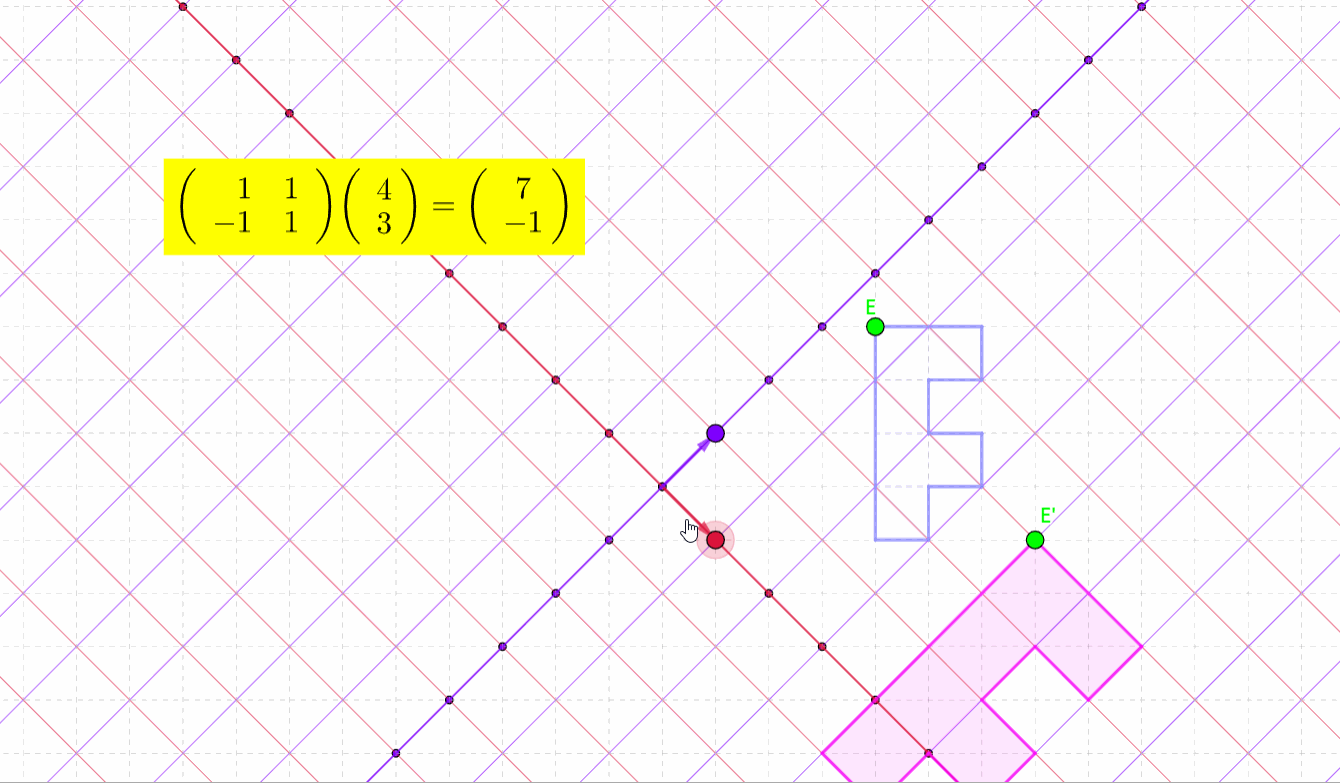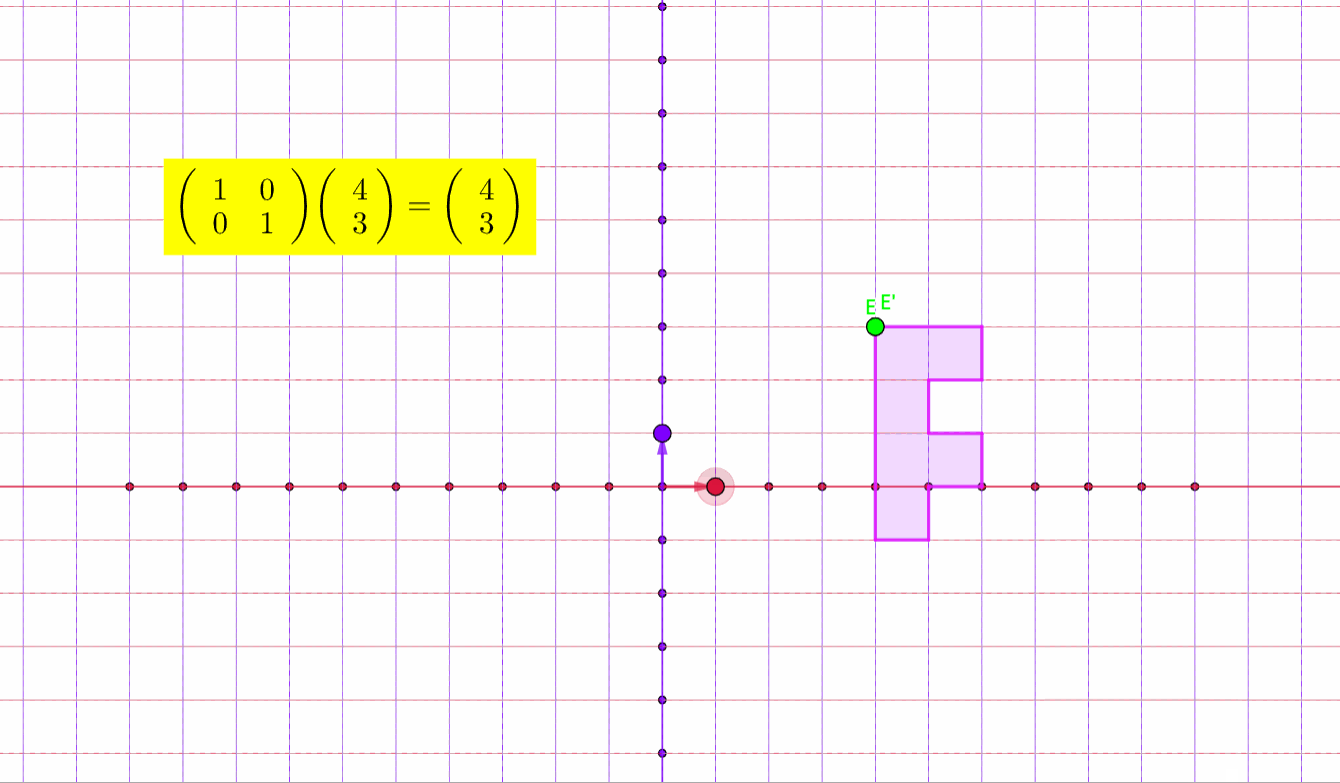
你可以清楚地看到粉色图形随着A的变换而变换

标准矩阵

$A$也称为标准矩阵，可以发现图形进行线性变换最重要的是$A$，因为$A$的不同导致了图形不同的变换

因此研究标准矩阵是重要的一环

这里形式化定义一个函数$T(x)=Ax$

由于是线性变换满足线性

①$T(cx)=c~T(x)$

②$T(ax+by)=a~T(x)+b~T(y)$

矩阵可以完成刚体变换、仿射变换、投影变换

①平移变换

严格来说平移不属于线性变换，但可以通过增加一个维度（齐次坐标系）来完成平移

$\begin{bmatrix}1&0&t_x \\ 0&1&t_y \\ 0&0&1 \end{bmatrix}$

而此时点的位置为$\begin{bmatrix}x\\y\\1 \end{bmatrix}$

通过增加一维来完成$\begin{cases}x'=x+t_x \\ y'=y+t_y \\ z=1 \end{cases}$

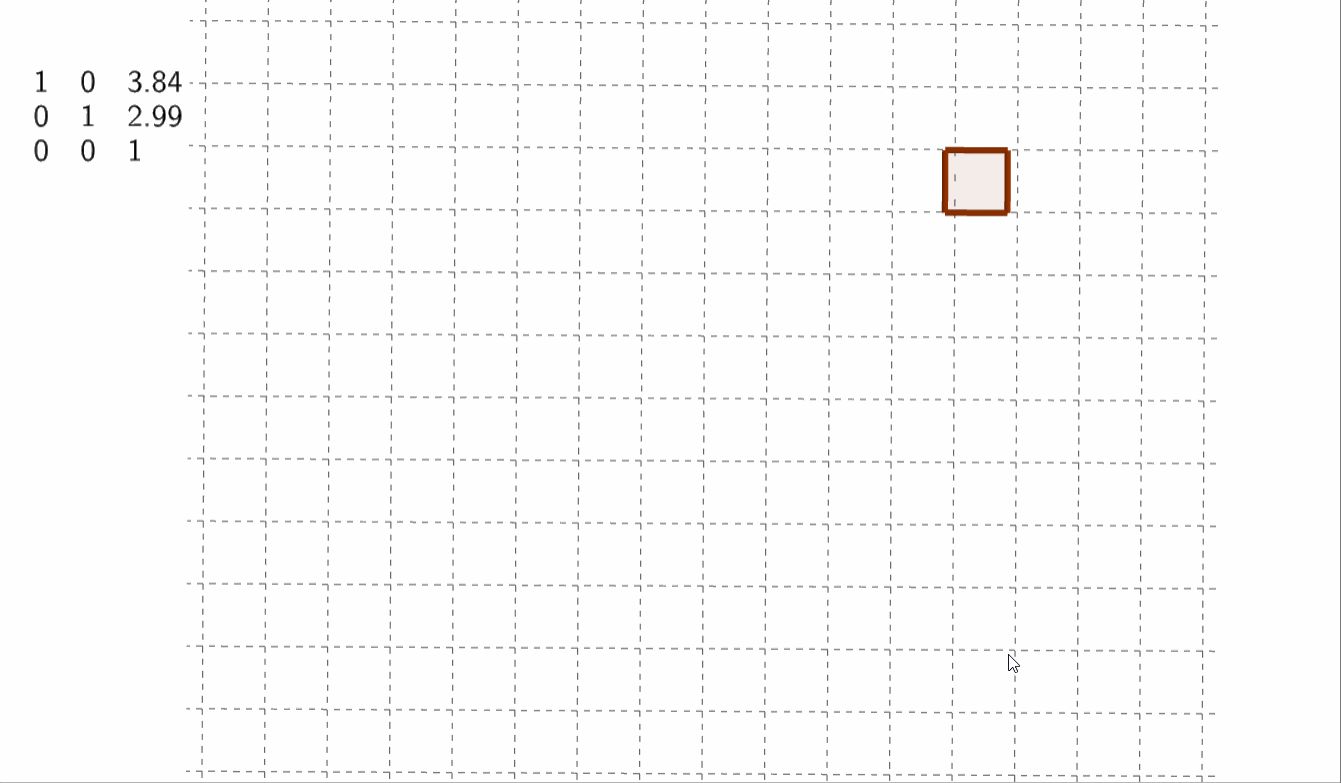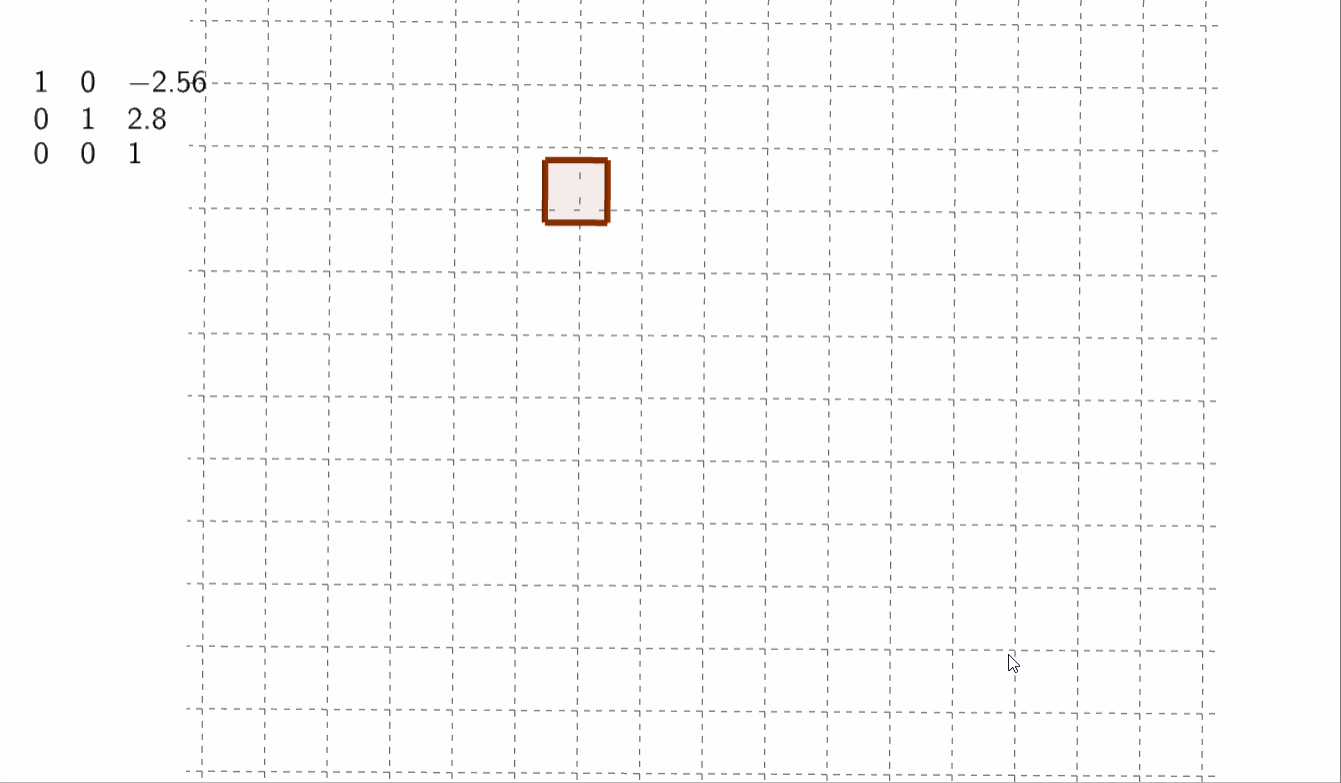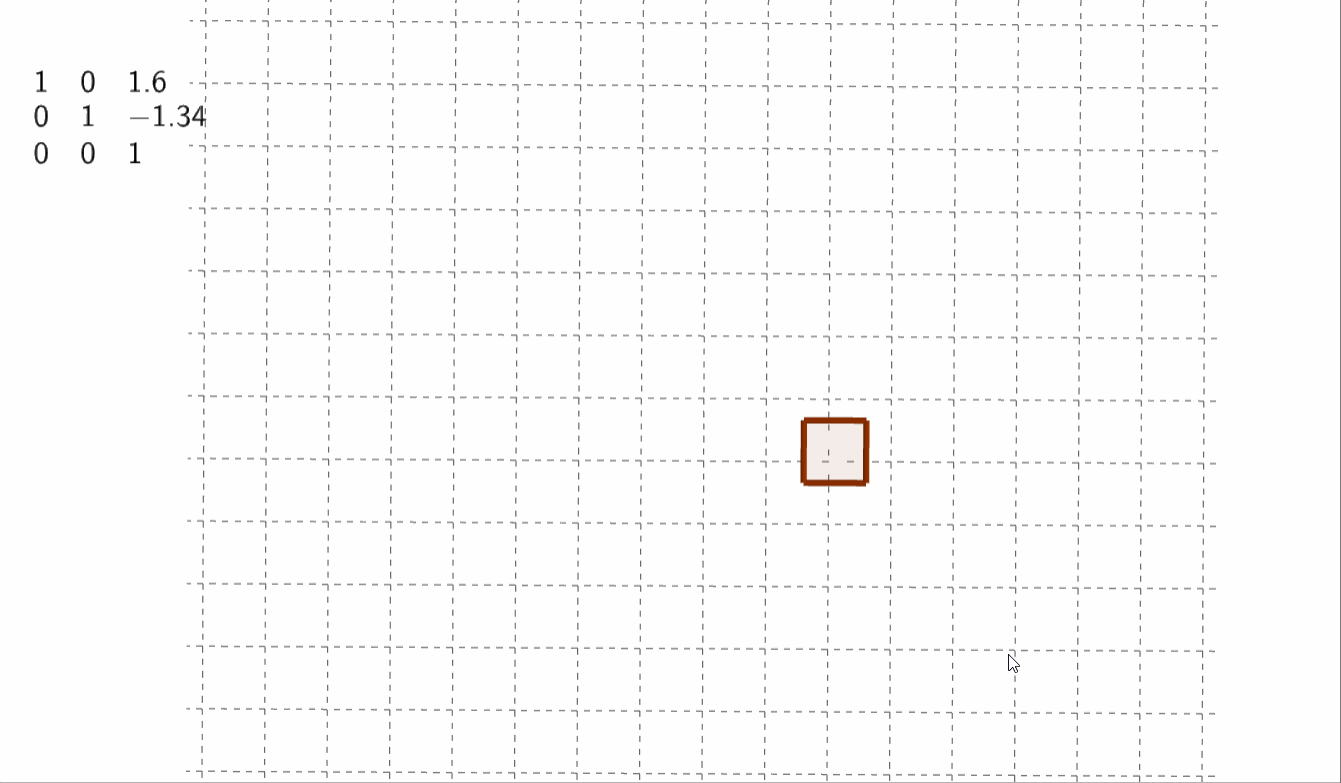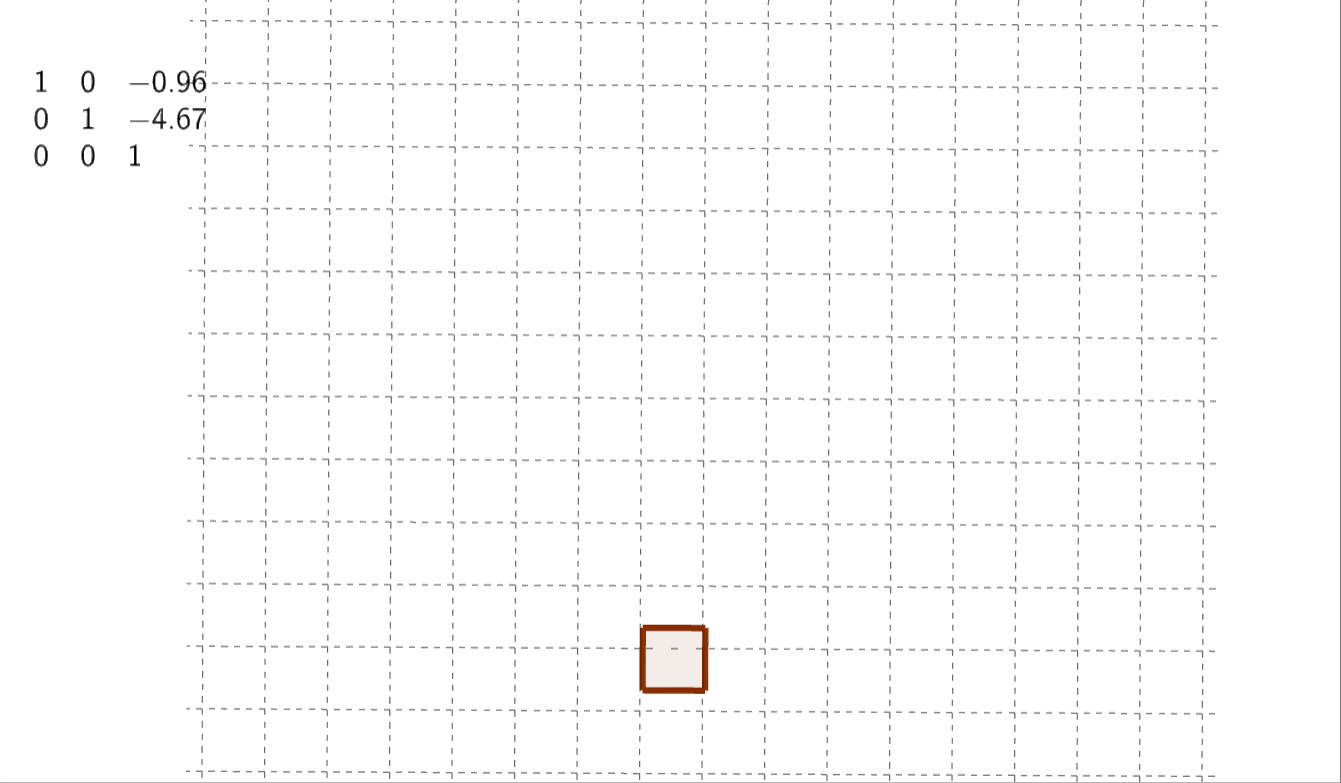
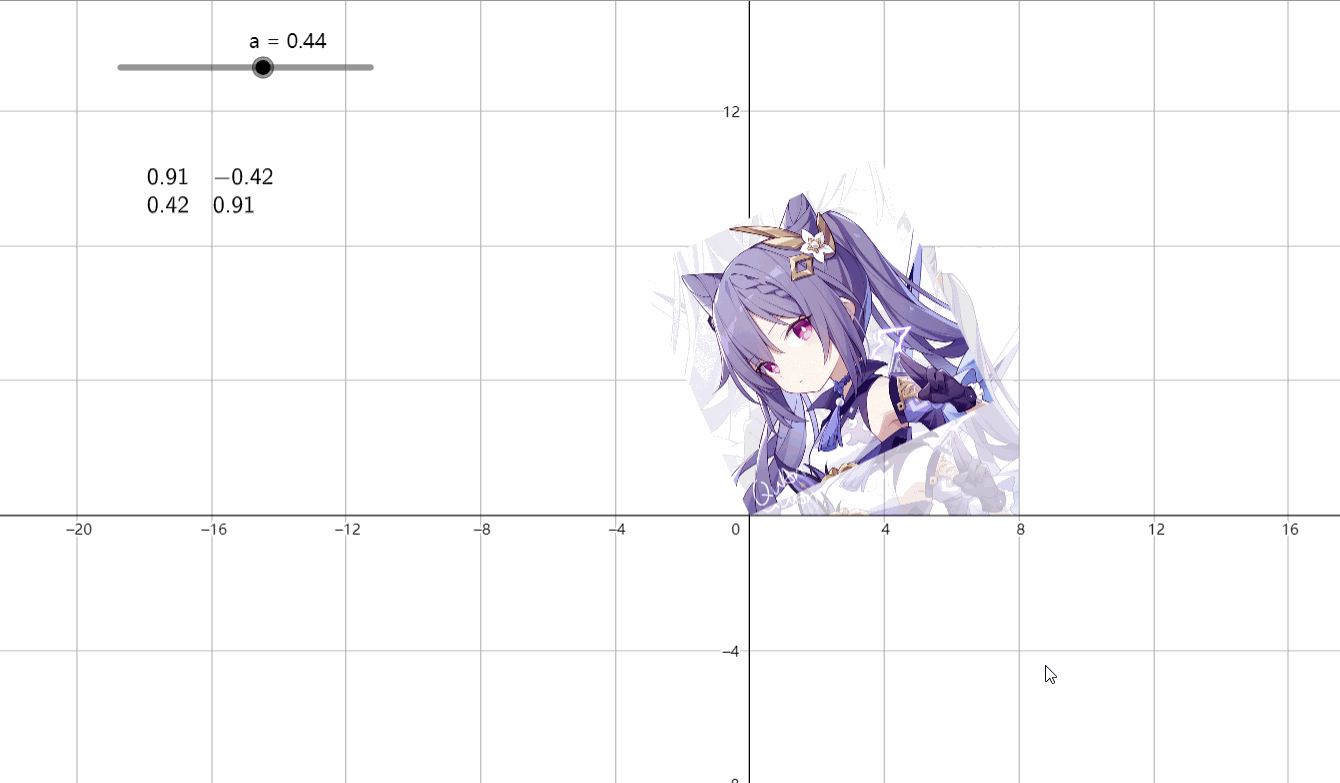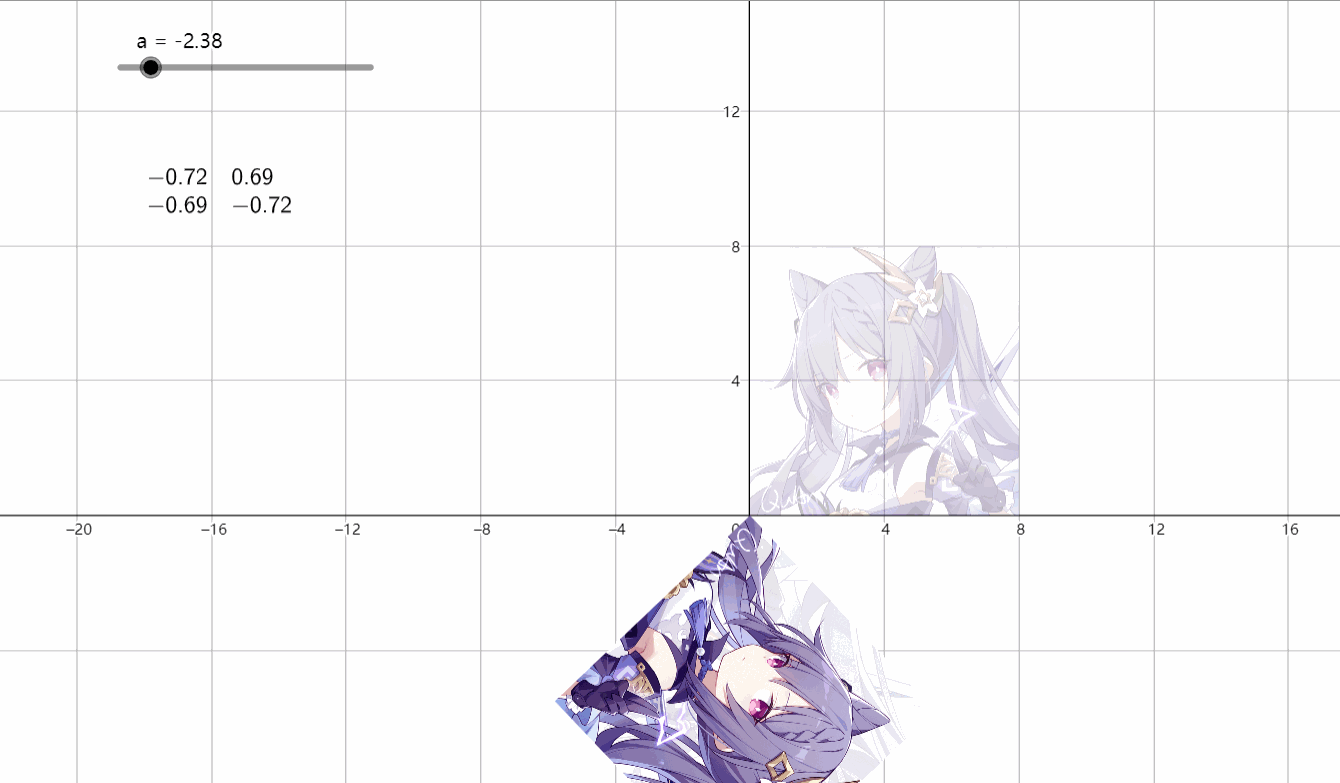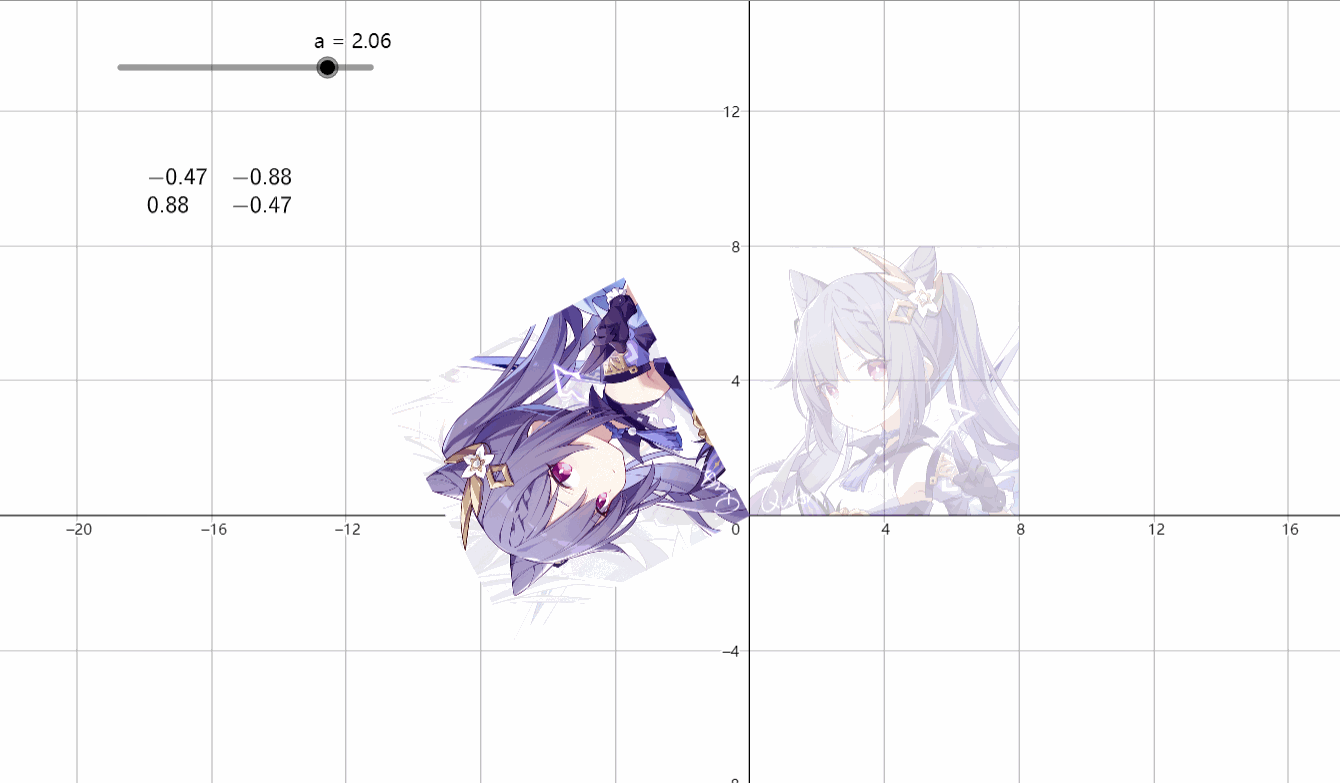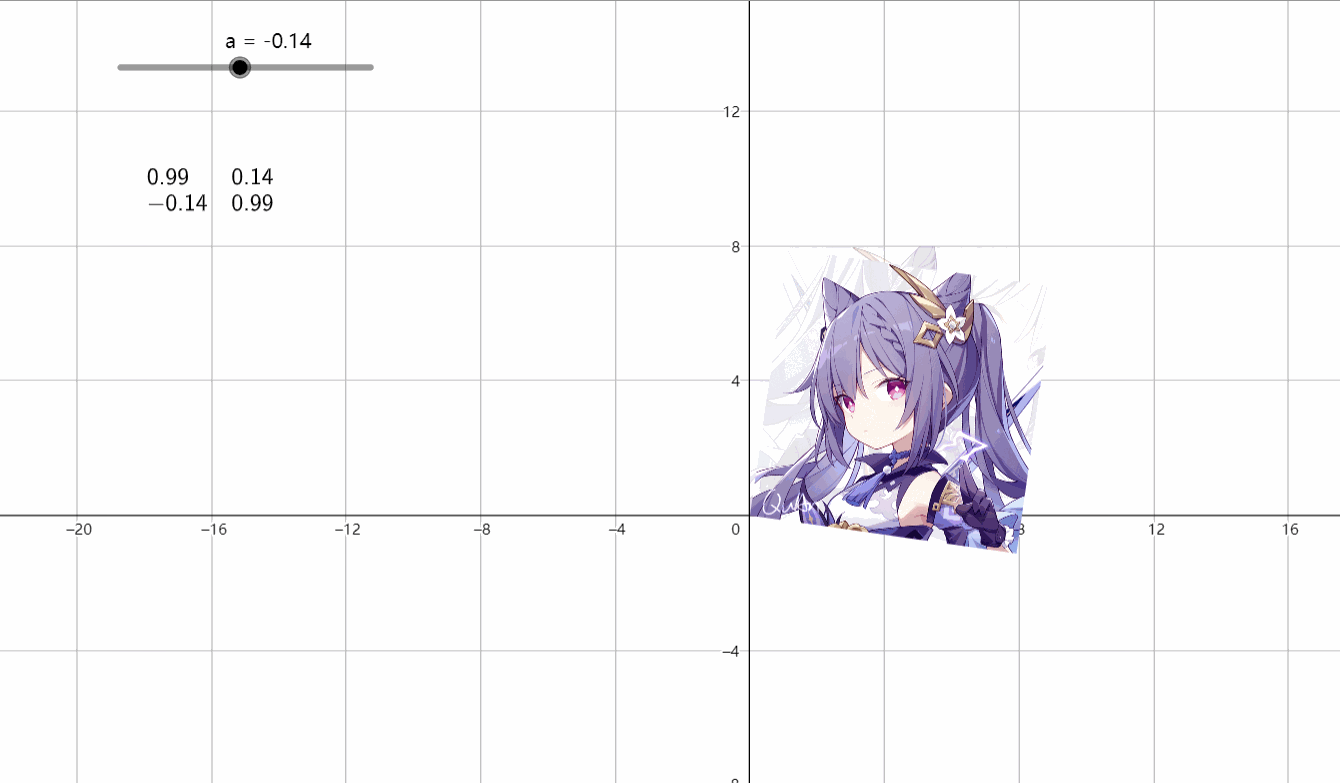
②旋转变换

这属于线性变换

$\begin{bmatrix}cos~x&-sin~x \\ sin~x&cos~x \end{bmatrix}$

而x为按逆时针所要旋转的角度

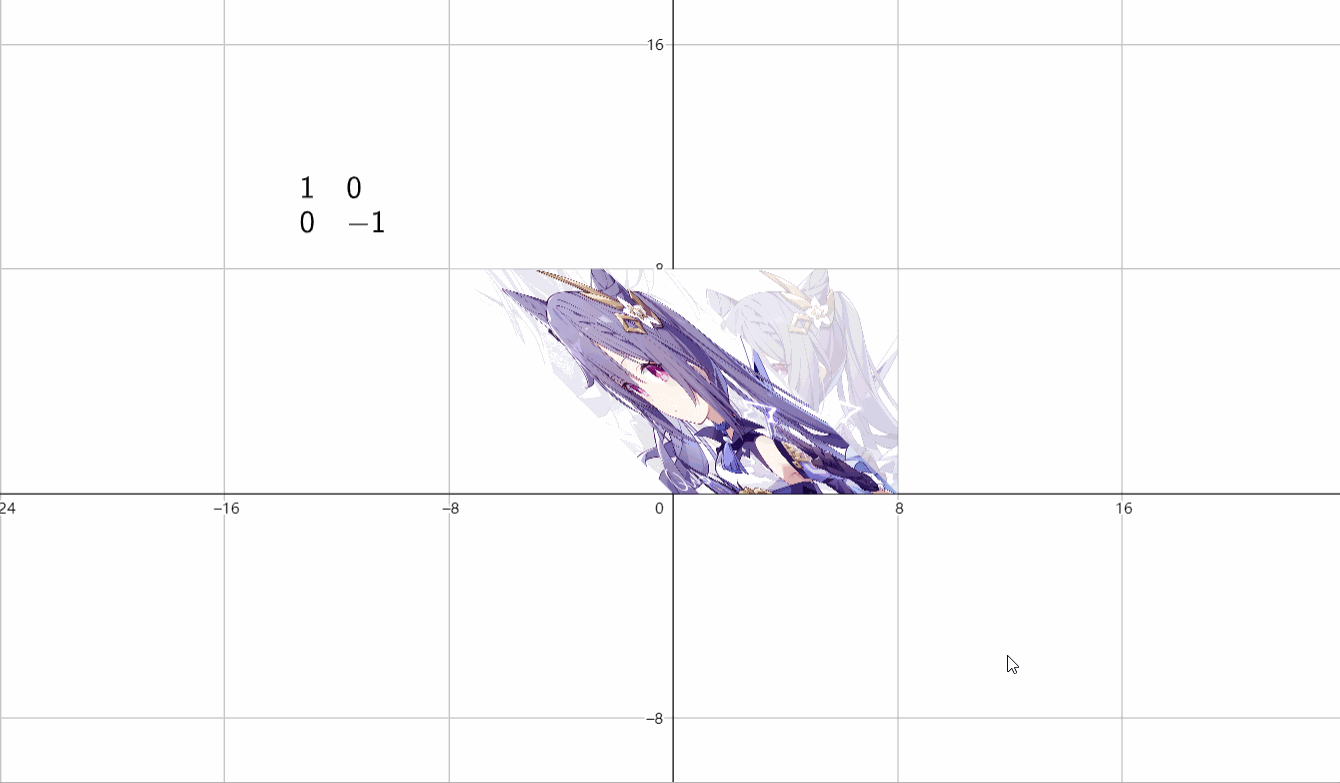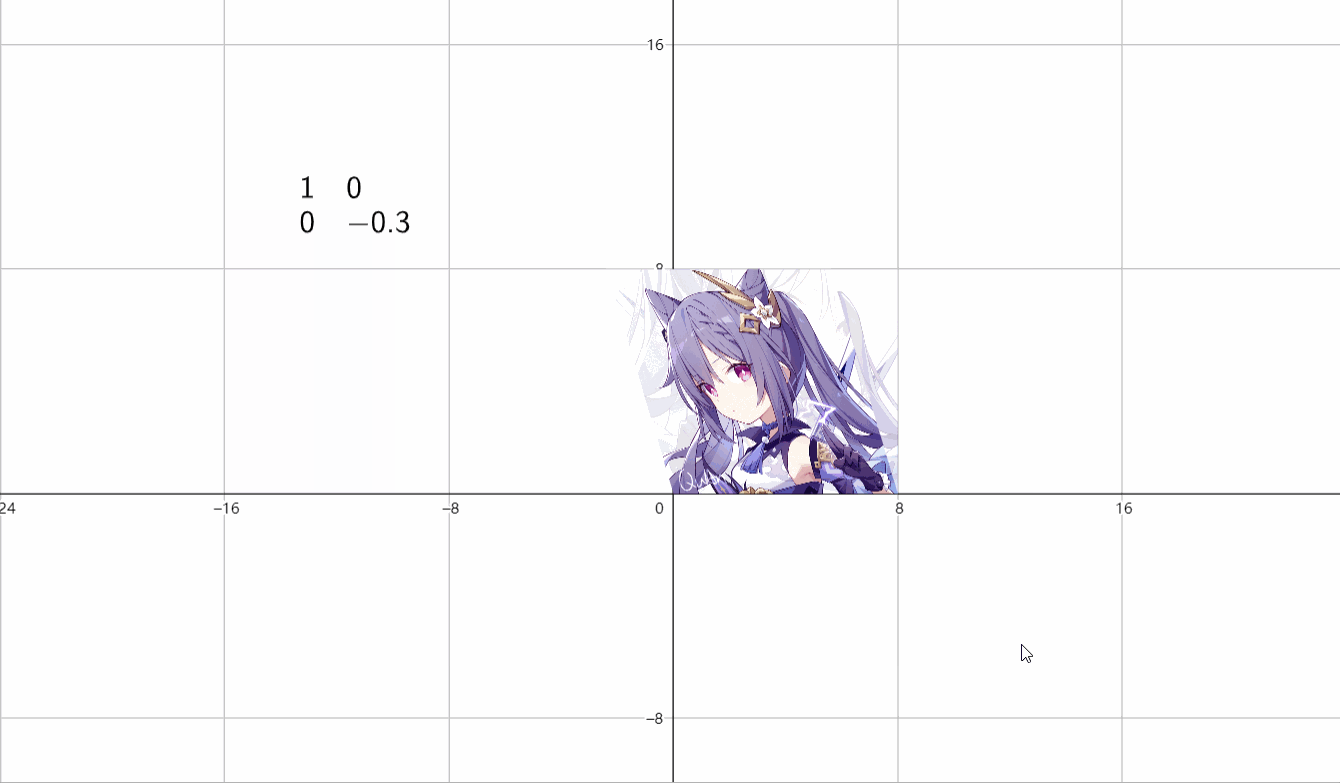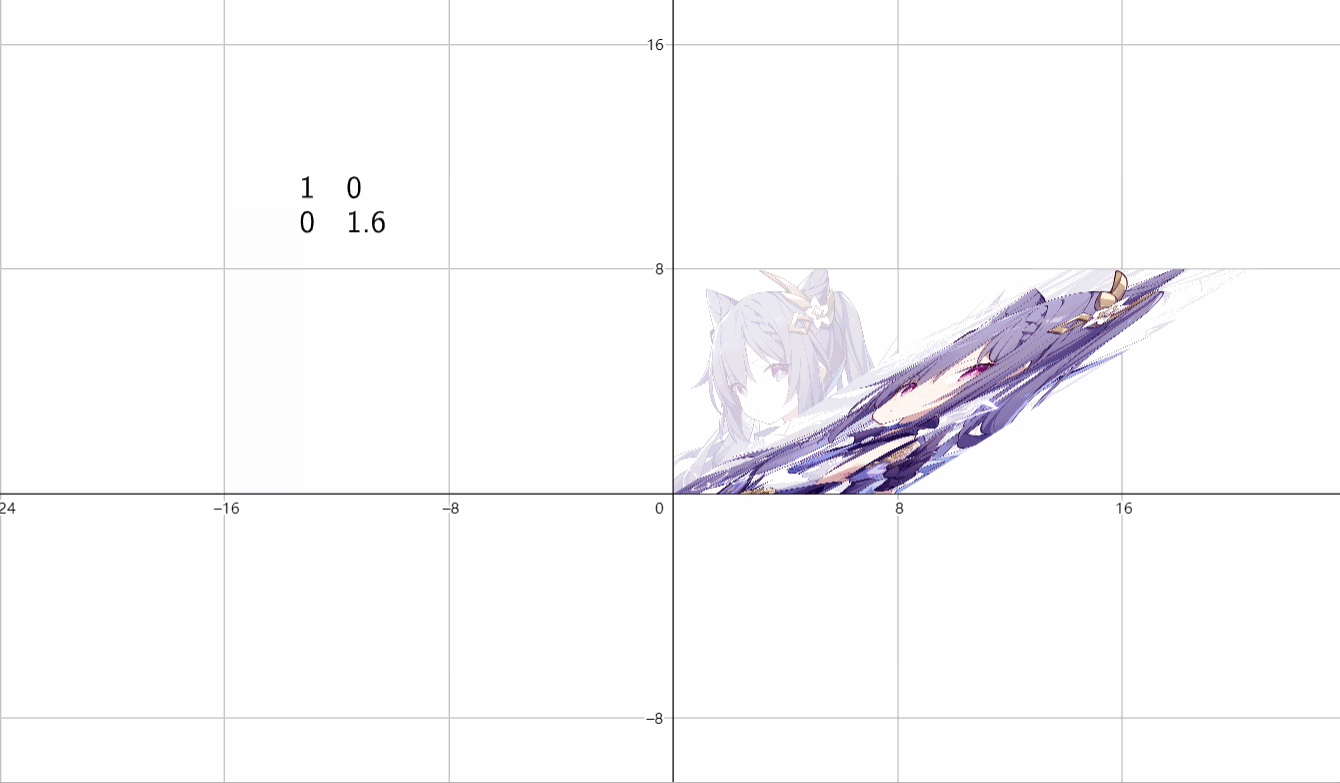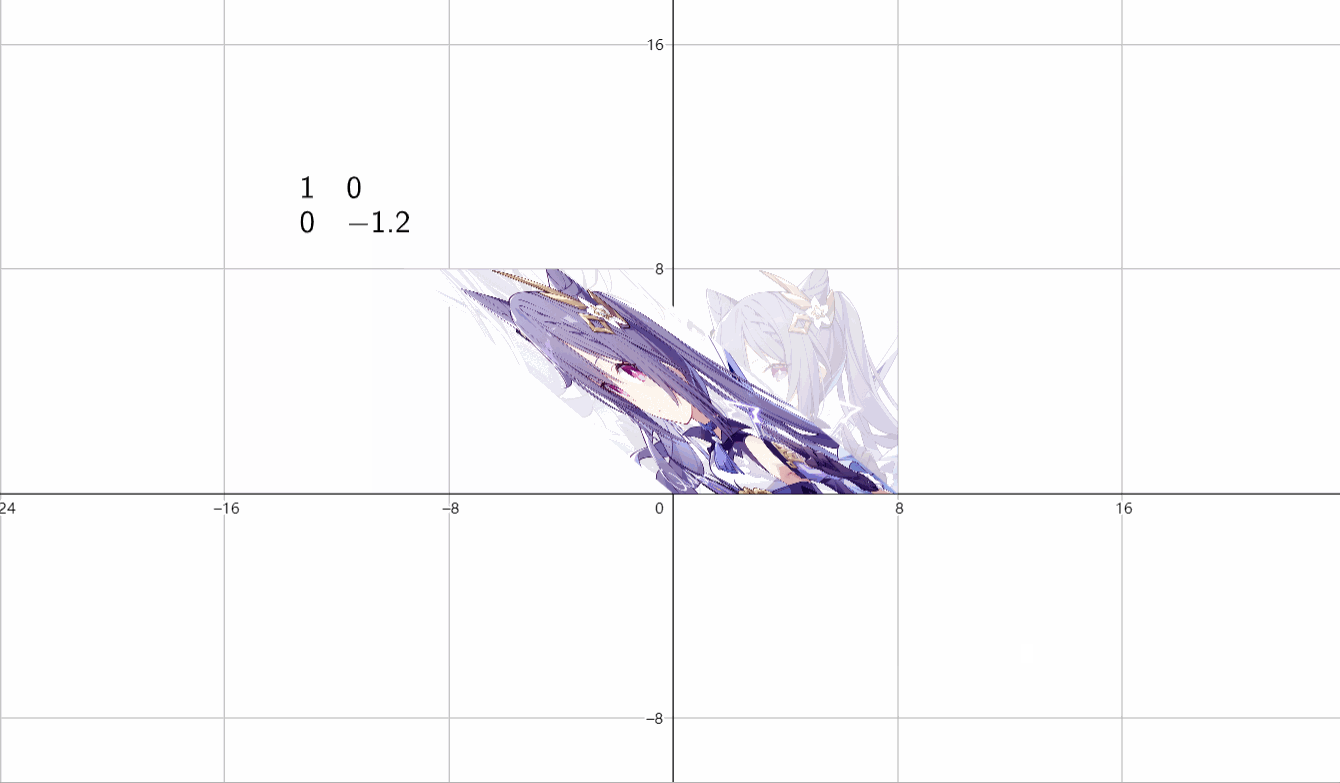
③对称变换

(1)关于$x$轴变换

$\begin{bmatrix}1&0 \\ 0&-1 \end{bmatrix}$

(2)关于$y$轴变换

$\begin{bmatrix}-1&0 \\ 0&1 \end{bmatrix}$

(3)关于$x=y$对称

$\begin{bmatrix}0&1 \\ 1&0 \end{bmatrix}$

(4)关于$x=-y$对称

$\begin{bmatrix}0&-1 \\ -1&0 \end{bmatrix}$

(5)关于原点对称

$\begin{bmatrix}-1&0 \\ 0&-1 \end{bmatrix}$

如何记住？

这里我推荐直接画个基向量，然后根据对称画出对称的基向量，然后就能得出了

④伸缩变换

(1)水平伸缩

$\begin{bmatrix}k&0 \\ 0&1 \end{bmatrix}$

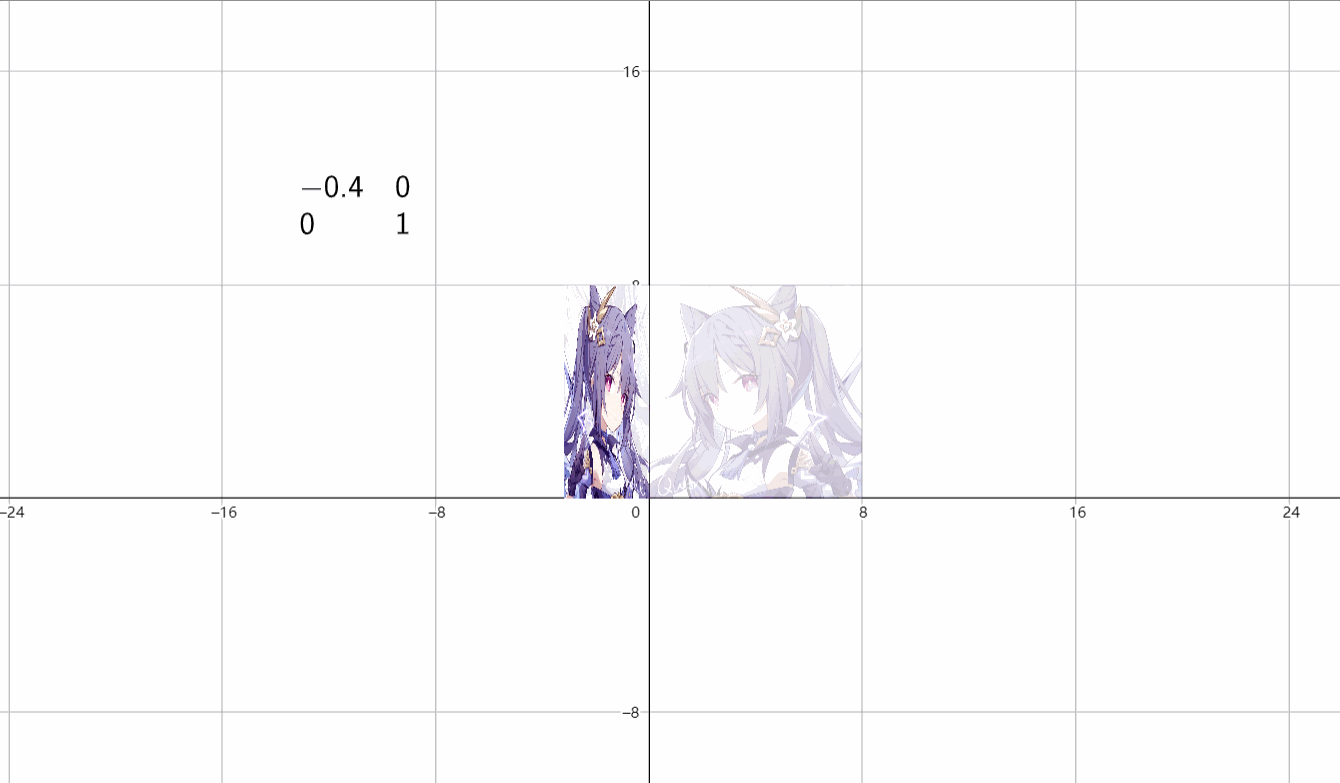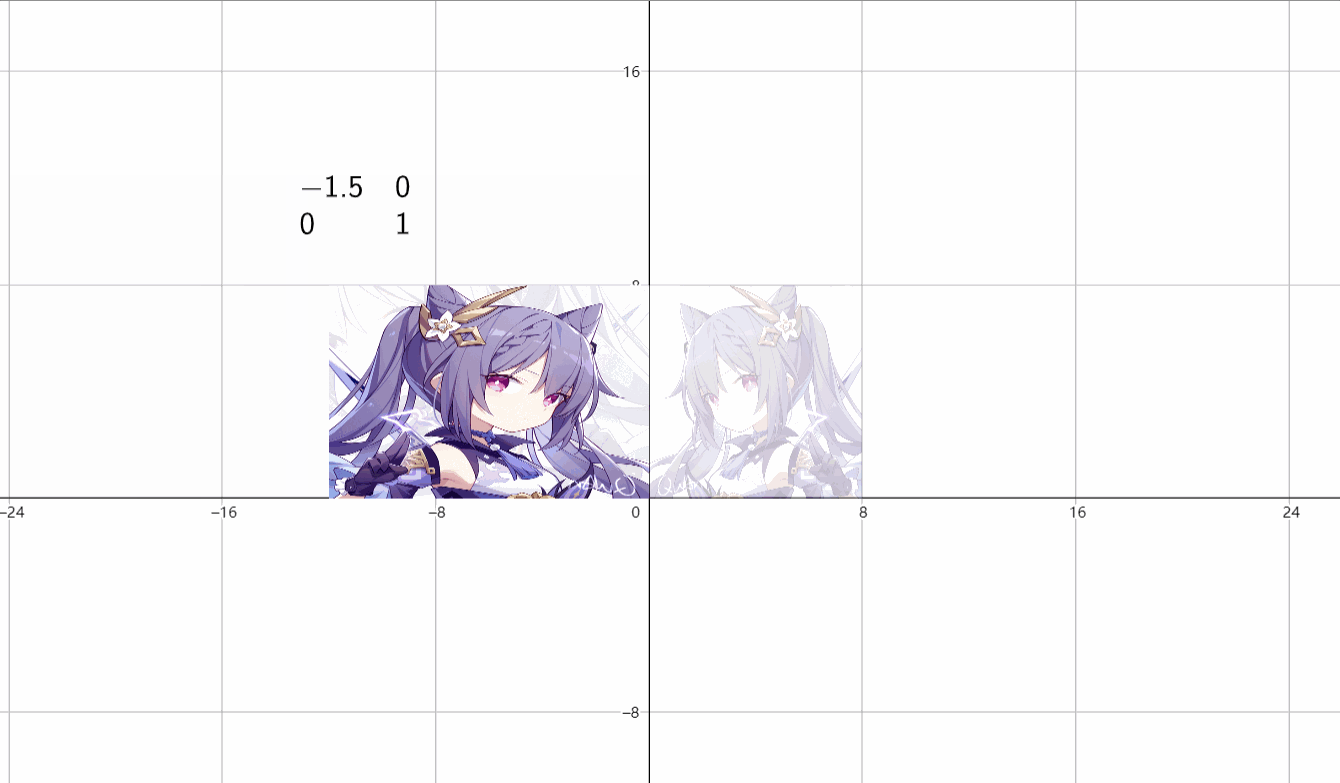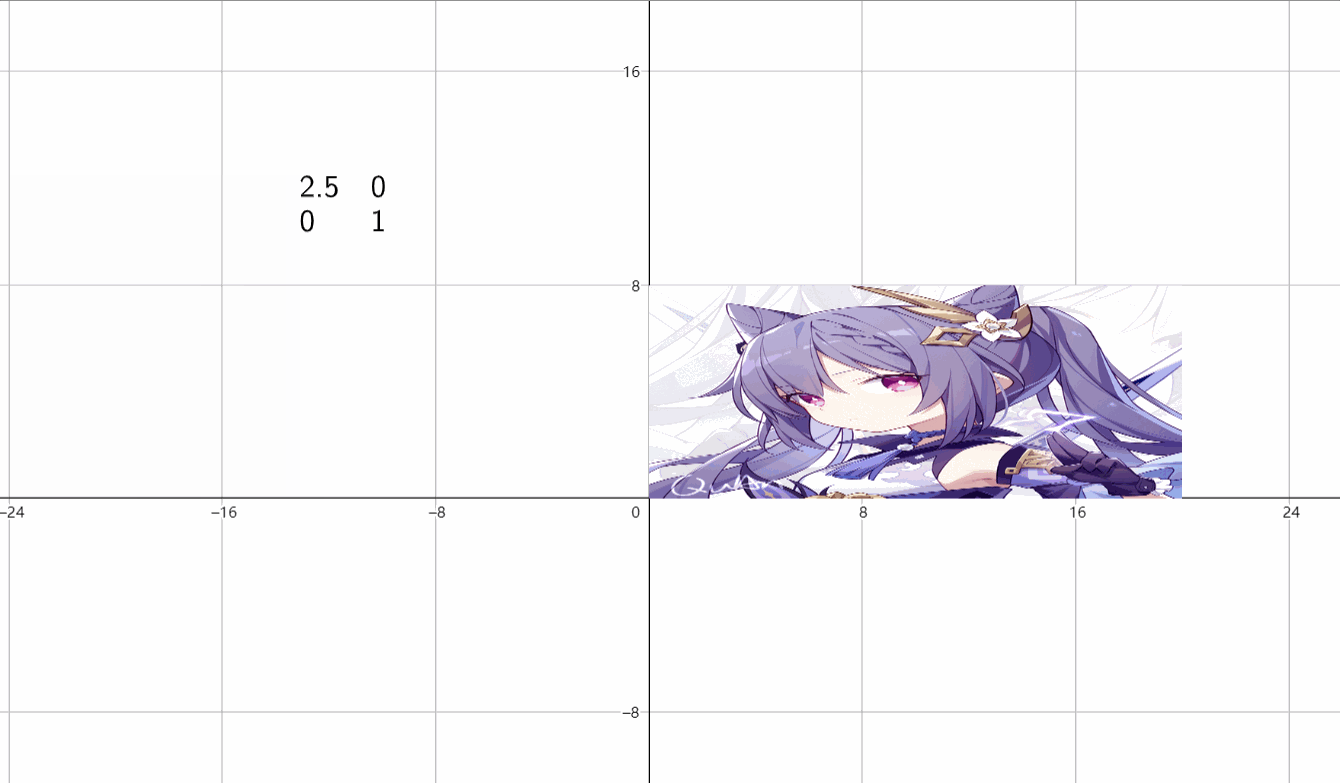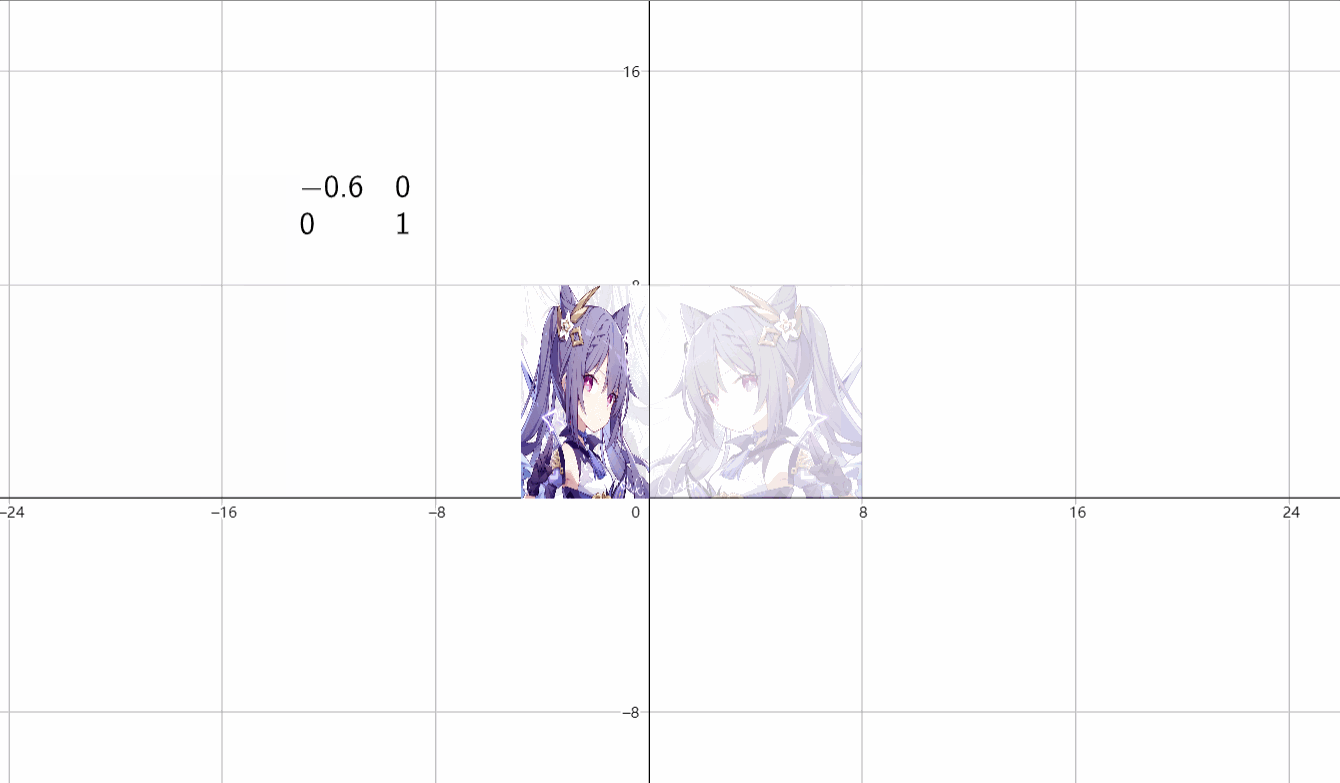
(2)垂直伸缩

$\begin{bmatrix}1&0 \\ 0&k \end{bmatrix}$

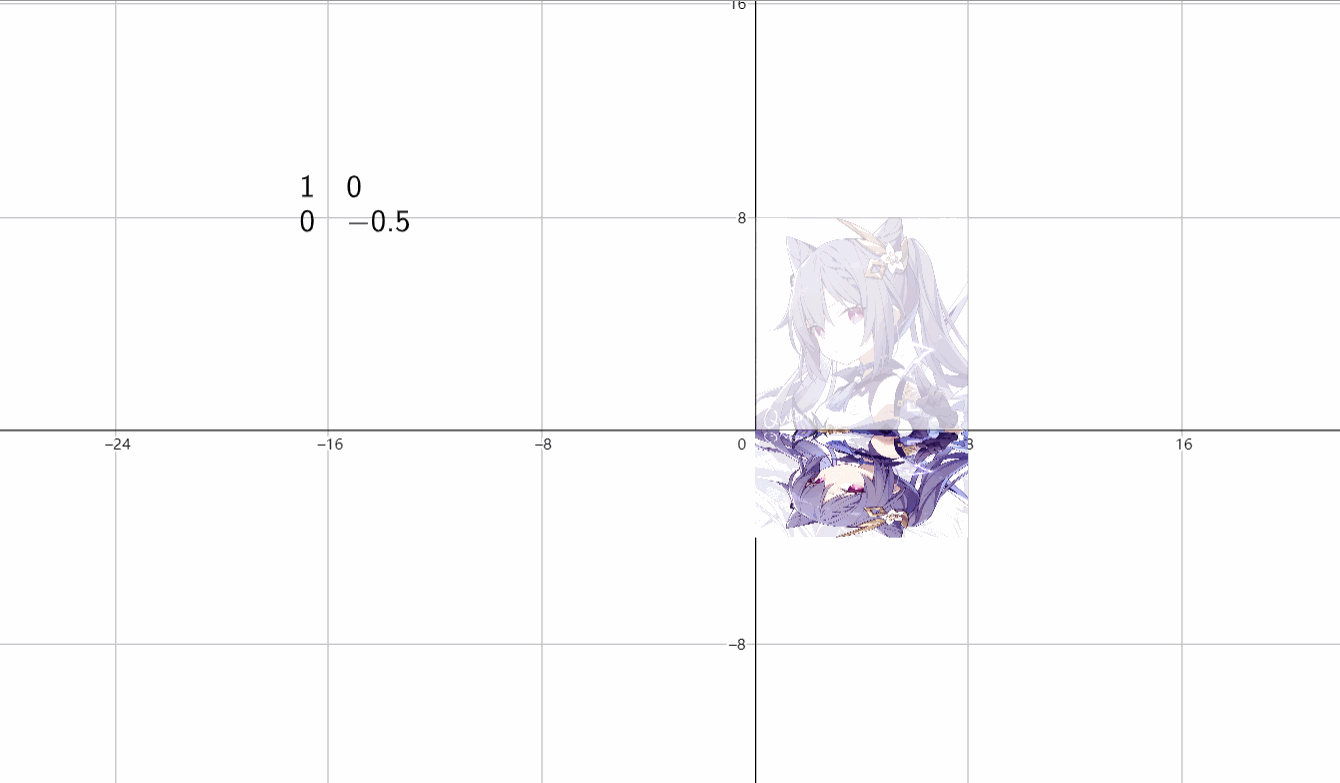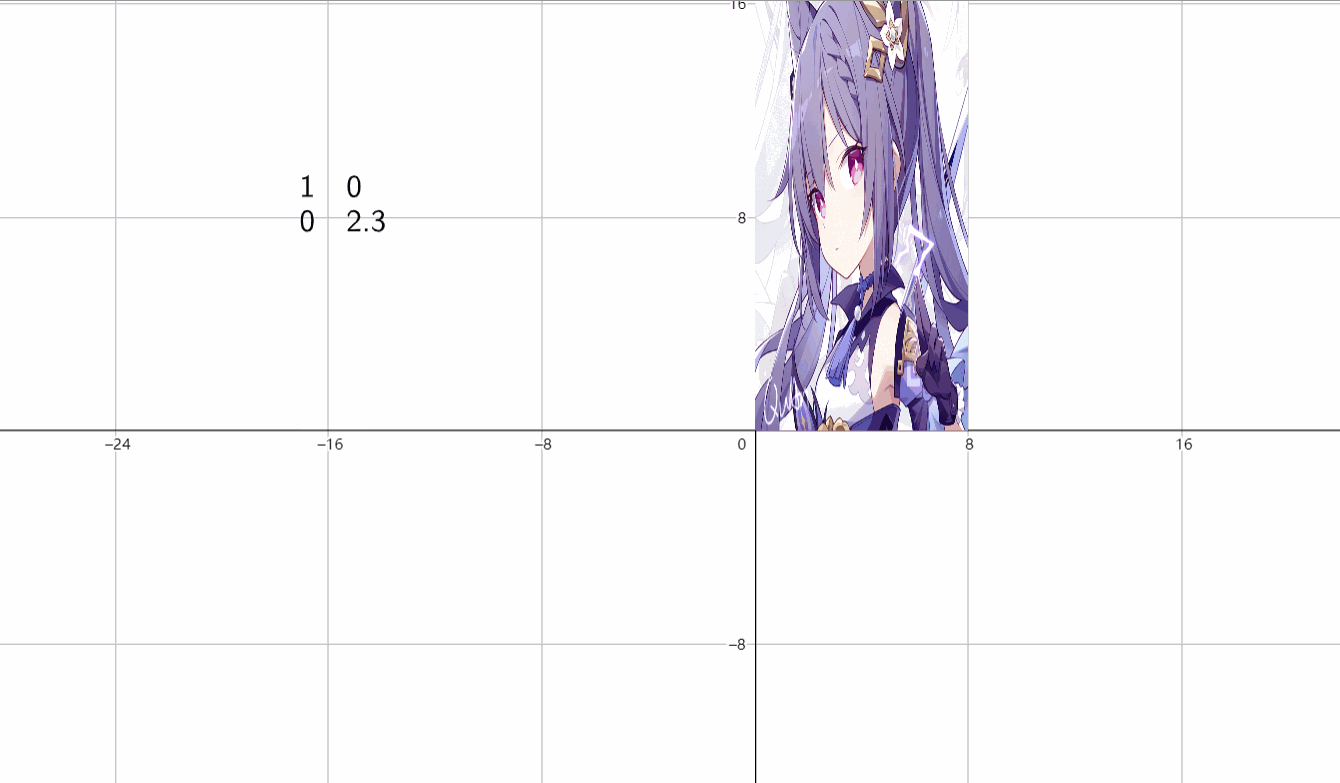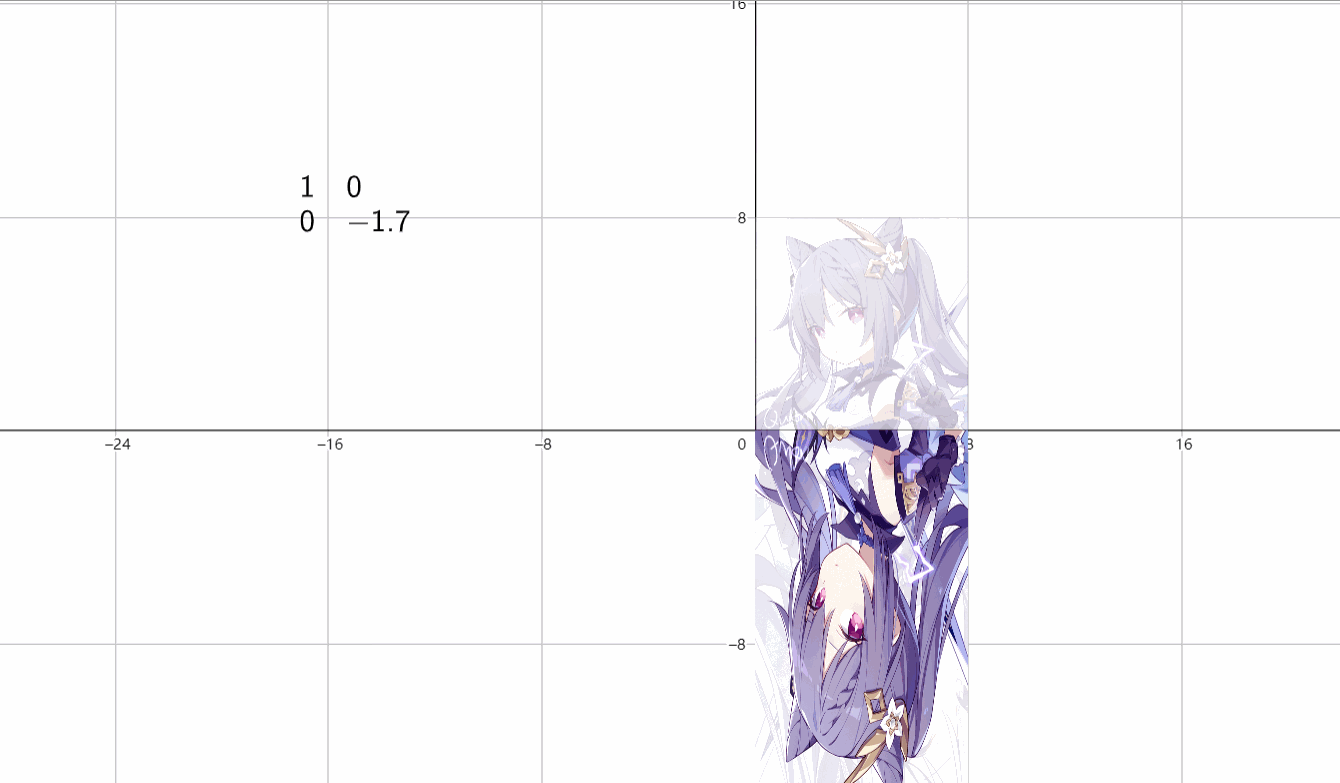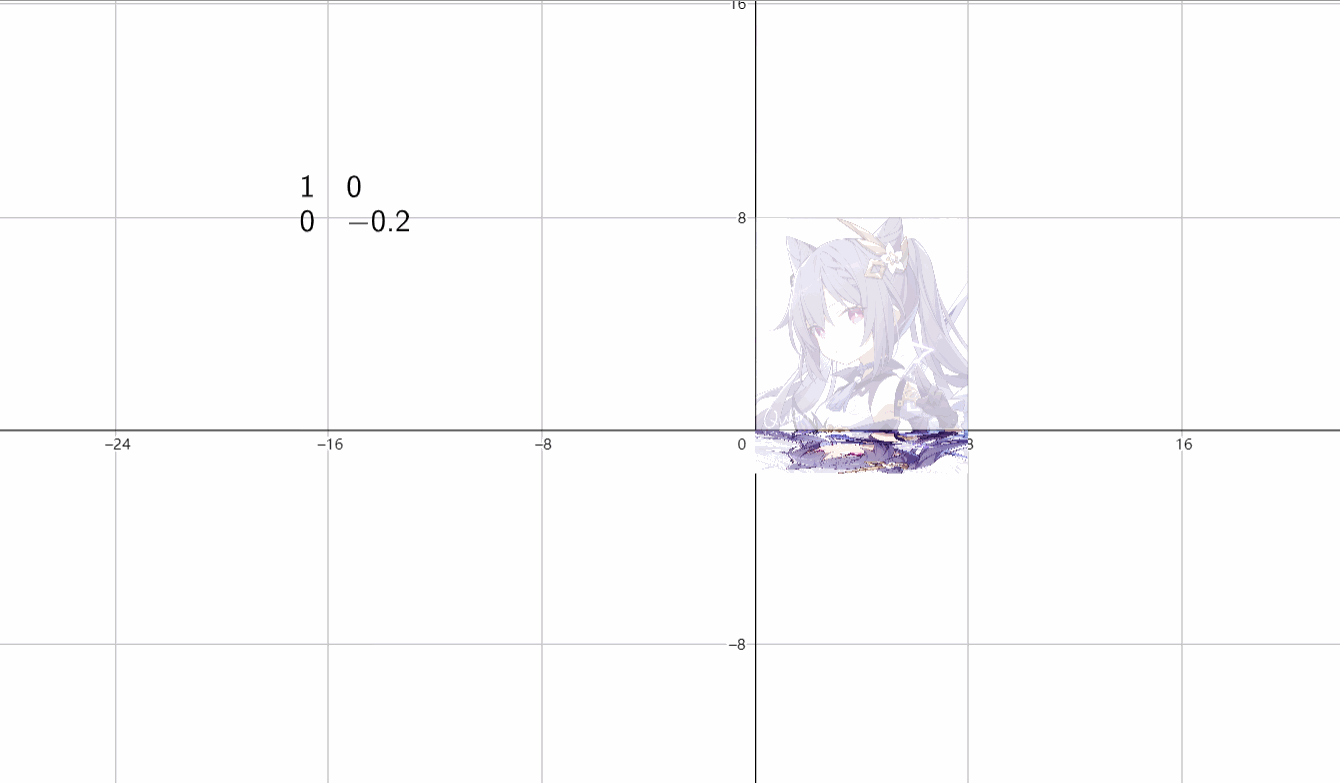
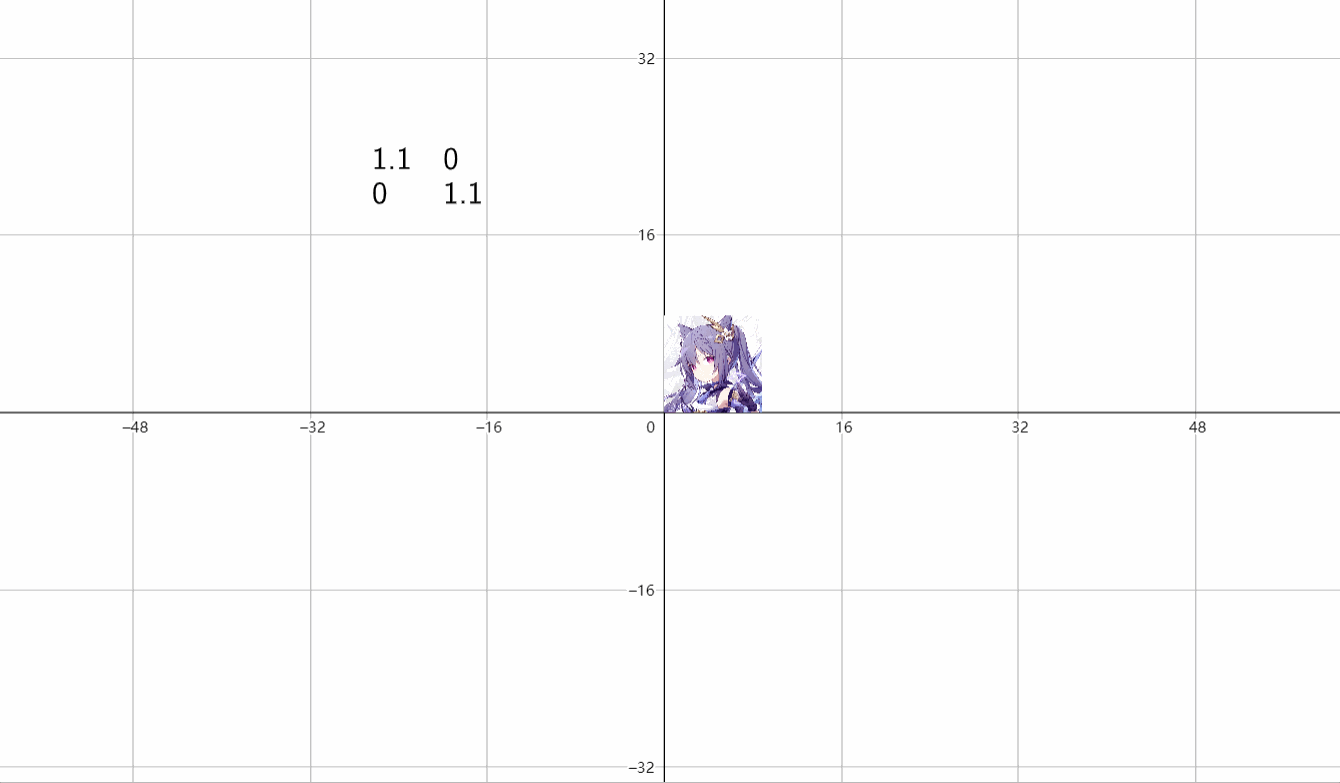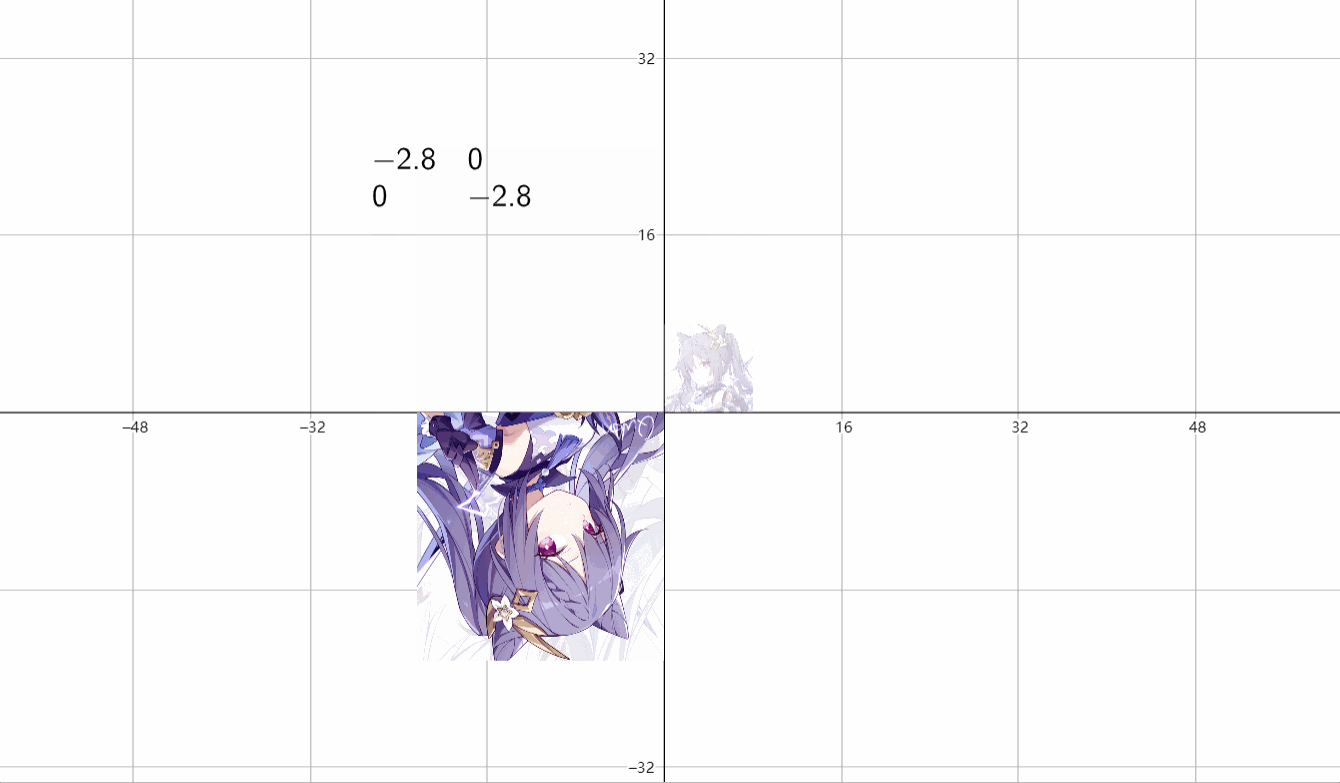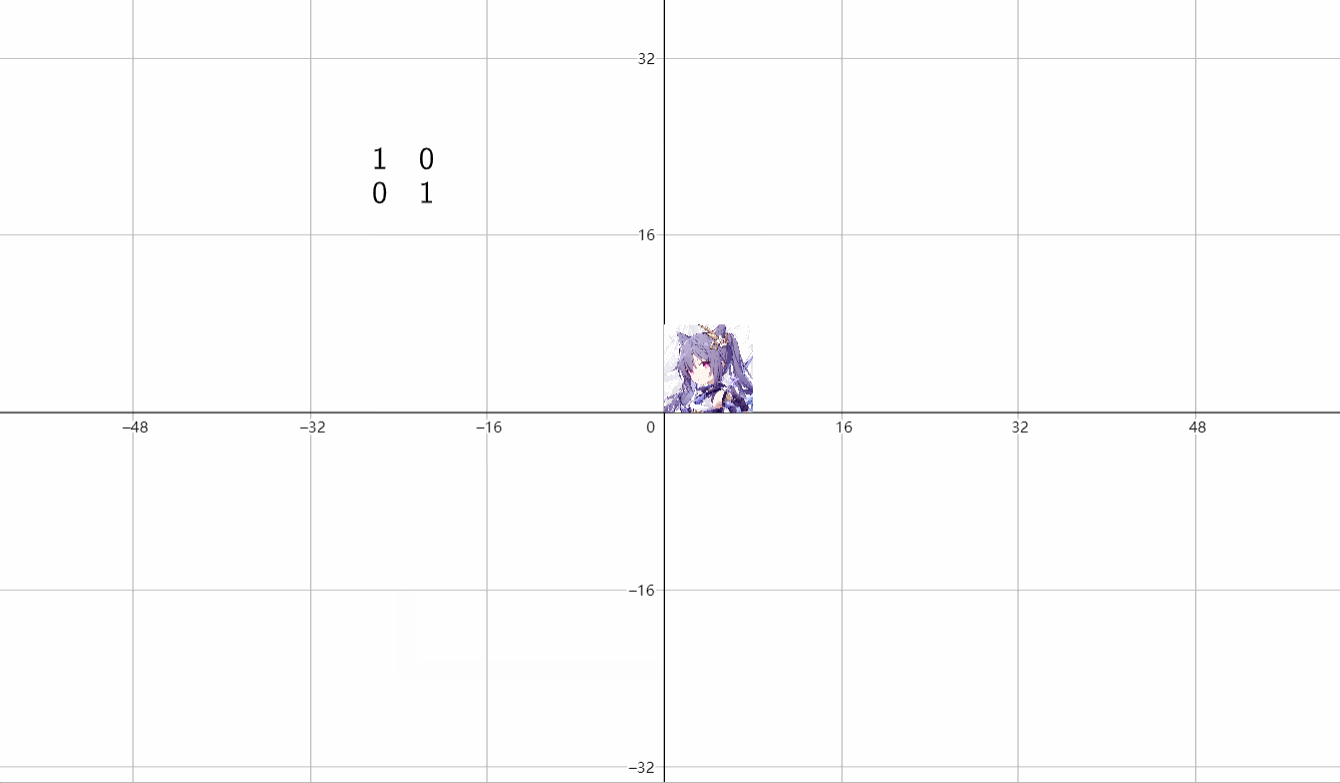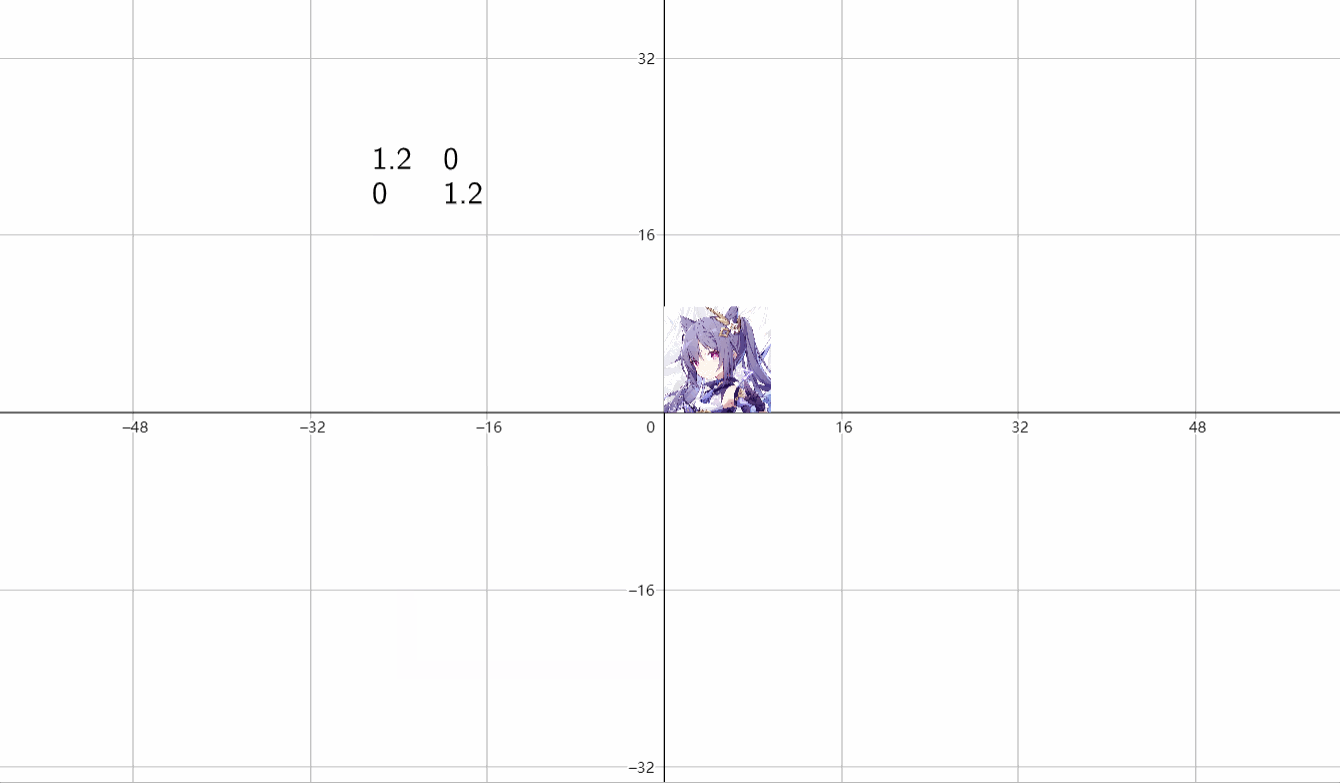
(3)放缩

$\begin{bmatrix}k&0 \\ 0&k \end{bmatrix}$

⑤剪切变换

(1)水平剪切

$\begin{bmatrix}1&k \\ 0&1 \end{bmatrix}$

(2)垂直剪切

$\begin{bmatrix}1&0 \\ k&1 \end{bmatrix}$

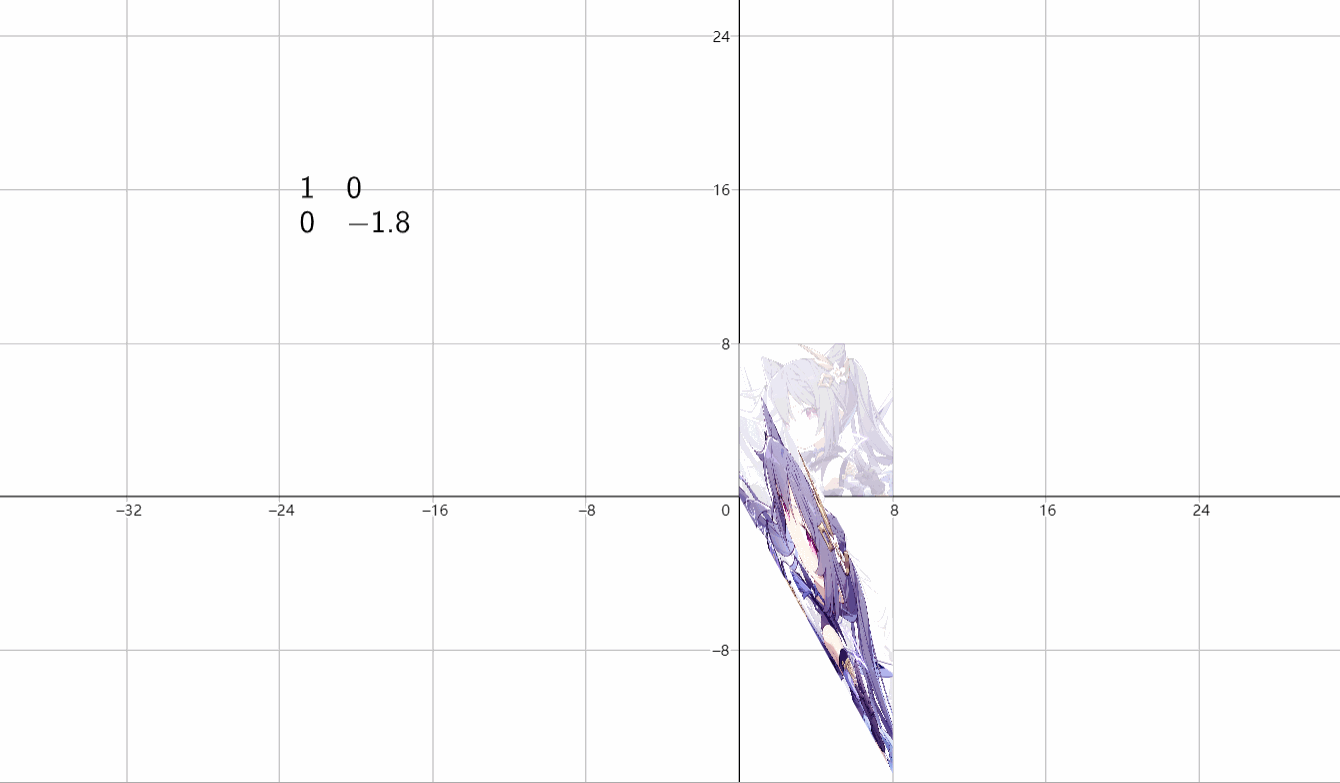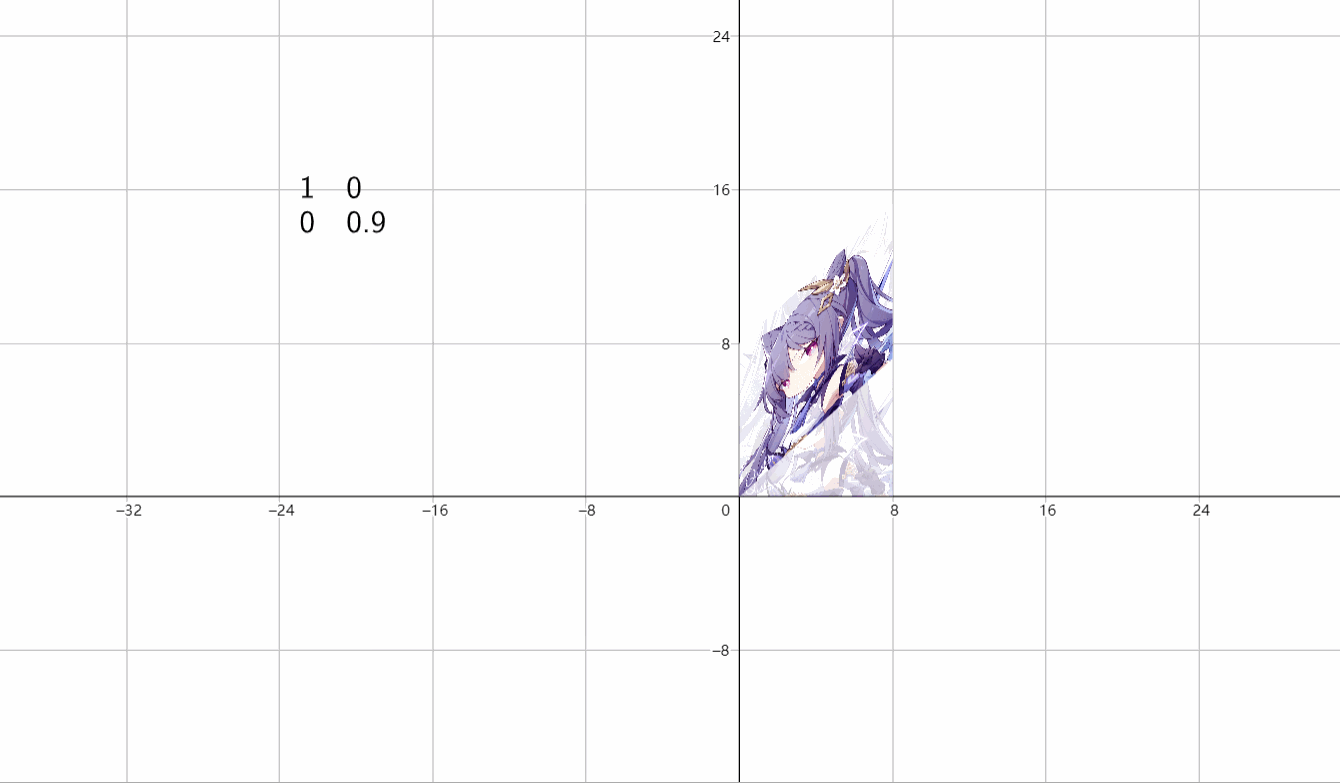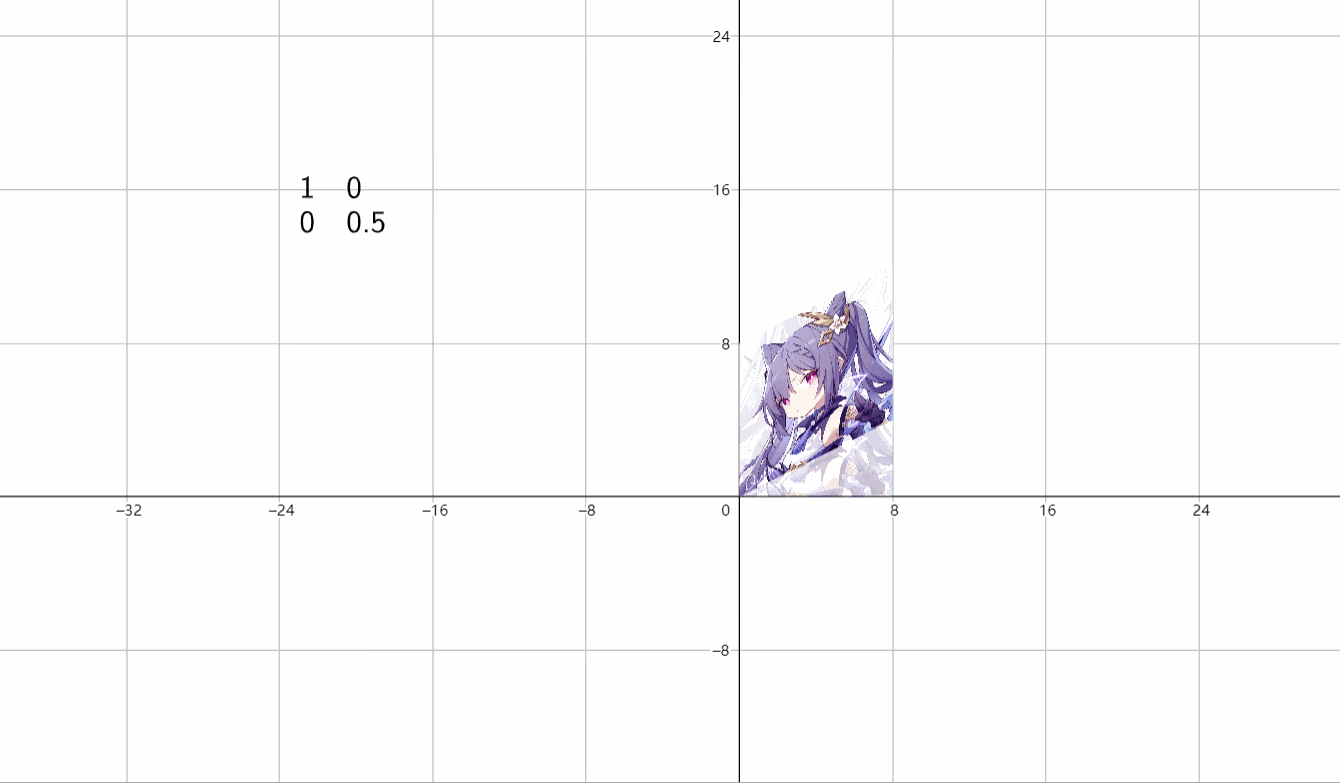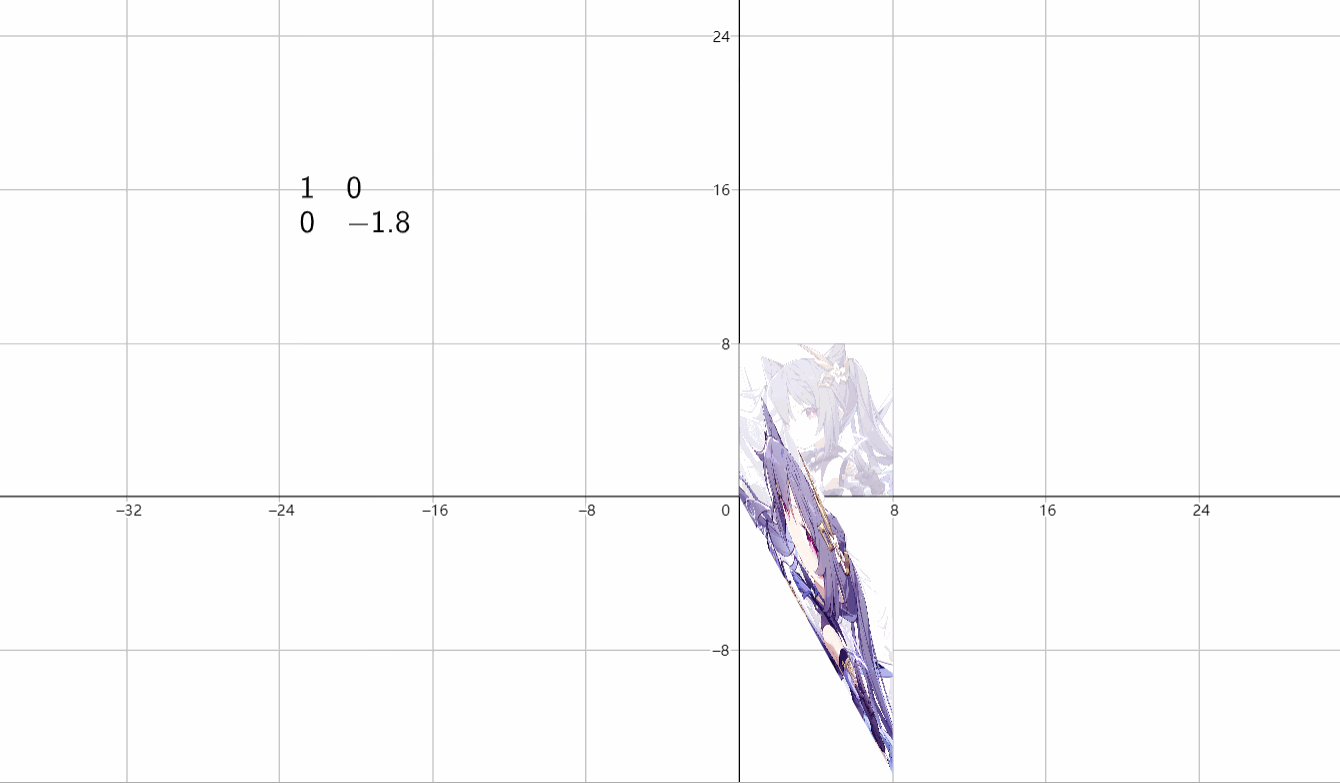
⑥投影变换

(1)投影至x轴

$\begin{bmatrix}1&0 \\ 0&0 \end{bmatrix}$

(2)投影至y轴

$\begin{bmatrix}0&0 \\ 0&1 \end{bmatrix}$

由于投影至一条线，因此无法看到，这里不做演示。但如果是3维投影到2维情况就不一样了，可以将一个立体物体变成二维，而如果这时候将投影后的图像涂黑，就变成了影子

五、矩阵运算性质

点击查看详细内容

注：这一块内容仅说明运算性质

基本术语

零空间用$0_{m×n}$表示

矩阵元素用$a_{ij}$表示，$i$为行，$j$为列（当然按照计算机传统，默认从0开始）

列向量用$a_i$表示，一般一个矩阵会用$\begin{bmatrix}a_1&a_2& ...&a_n \end{bmatrix}$表示

行向量也用$a_i$表示，一般一个矩阵会用$\begin{bmatrix}a_1 \\ a_2 \\ \vdots \\ a_n \end{bmatrix}$表示

单位矩阵用$E$或$I_m$表示

标量乘法、加法

①$A+B=B+A$（交换律）

②$(A+B)+C=A+(B+C)$（结合律）

③$(r+s)A=rA+sA$（分配律）

④$r(A+B)=rA+rB$（分配律）

⑤$r(sA)=(rs)A$（结合律）

matrix matrix_add(matrix a,matrix b){
	//作用：矩阵加法a+b
	if(a.col != b.col || a.row != b.row){
		printf("错误：维数不匹配");
		exit(-1);
	}
	matrix r;
	matrix_null(&r,a.row,a.col);
	for(int i = 0;i < a.row;i++){
		for(int j = 0;j < a.col;j++){
			r.base[i][j] = fraction_add(a.base[i][j],b.base[i][j]);
		}
	}
	return r;
}

matrix matrix_sub(matrix a,matrix b){
	//作用：矩阵减法a-b
	if(a.col != b.col || a.row != b.row){
		printf("错误：维数不匹配");
		exit(-1);
	}
	matrix r;
	matrix_null(&r,a.row,a.col);
	for(int i = 0;i < a.row;i++){
		for(int j = 0;j < a.col;j++){
			r.base[i][j] = fraction_sub(a.base[i][j],b.base[i][j]);
		}
	}
	return r;
}

matrix matrix_cmul(matrix a,Fraction C){
	//作用：标量乘法C*a
	matrix r;
	matrix_null(&r,a.row,a.col);
	for(int i = 0;i < a.row;i++){
		for(int j = 0;j < a.col;j++){
			r.base[i][j] = fraction_mul(a.base[i][j],C);
		}
	}
	return r;
}

matrix matrix_linear(Fraction C1,matrix a,Fraction C2,matrix b){
	//作用：矩阵线性组合C1*a+C2*b
	if(a.col != b.col || a.row != b.row){
		printf("错误：维数不匹配");
		exit(-1);
	}
	matrix r;
	matrix_null(&r,a.row,a.col);
	for(int i = 0;i < a.row;i++){
		for(int j = 0;j < a.col;j++){
			r.base[i][j] = fraction_add(fraction_mul(a.base[i][j],C1),fraction_mul(b.base[i][j],C2));
		}
	}
	return r;
}

矩阵乘法

$AB$是$A$的各列乘上$B$所对应的权

从单个元素来看得出重要公式

$(AB)_{ij}=∑_{k=0}^{n}a_{ik}b_{kj}$

然后根据这个重要公式编写代码

matrix matrix_mul(matrix a,matrix b){
	//作用：矩阵乘法A*B
	if(a.col != b.row){
		printf("错误：维数不匹配");
		exit(-1);
	}
	matrix r;
	matrix_null(&r,a.row,b.col);
	for(int i = 0;i < r.row;i++){
		for(int j = 0;j < r.col;j++){
			for(int k = 0;k < a.col;k++)
			r.base[i][j] = fraction_add(r.base[i][j],fraction_mul(a.base[i][k],b.base[k][j]));
		}
	}
	return r;
}

①$AB≠BA$一般情况不满足交换律！！！

因为不满足交换律，$B$乘上$A$就分为了两种方式

一个是左乘$AB$，一个是右乘$BA$

②$A(BC)=(AB)C$（结合律）

③$B(A+C)=BA+BC$（左分配律）

④$(A+C)B=AB+CB$（右分配律）

⑤$A(rB)=r(AB)$

⑥$I_mA=AI_m=A$

⑦不满足消去律，不能由$AB=AC$推出$B=C$

乘幂

$A^k=A.A...A$

①$A^0=I_m$

matrix matrix_pow(matrix a,int k){
	//作用：矩阵乘幂A^k
	if(a.row != a.col){
		printf("错误：维数无法匹配");
		exit(-1);
	}
	matrix r;
	matrix_identity(&r,a.row);
	while(k--){
		r = matrix_mul(r,a);
	}
	return r;
}

转置

行向量是指$\begin{bmatrix}a_1&a_2&...&a_n \end{bmatrix}$的向量

行向量本质上是和列向量一样的，只是表达上有所区别

比如从行向量看待的$\begin{bmatrix}1&2 \end{bmatrix}$和从列向量看待的$\begin{bmatrix}1 \\ 2 \end{bmatrix}$是一样的

中间经过一个叫转置的运算，记作$A^T$

转置是将原本从列/行向量看待的矩阵变成从行/列向量看待的矩阵

从单个元素来看就是$a_{ij}=a_{ji}$

矩阵乘法从不同角度所做的运算是不同的，但结果相似的
列向量看待矩阵乘法是Ax把右侧看作未知量，为左乘
行向量看待矩阵乘法时就是xA把左侧看作未知量，为右乘

比如$\begin{bmatrix}1&2 \\ 3&4 \end{bmatrix}\begin{bmatrix}1\\2\end{bmatrix}=1\begin{bmatrix} 1 \\ 3\end{bmatrix}+2\begin{bmatrix} 2 \\ 4\end{bmatrix}=\begin{bmatrix}5 \\ 11\end{bmatrix}$

从行向量看待，就需要将这个式子中的矩阵进行转置并且把左乘改成右乘

从行向量看待的乘法就要从行来看待$\begin{bmatrix}1&2 \end{bmatrix}\begin{bmatrix}1&3 \\ 2&4 \end{bmatrix}=1\begin{bmatrix}1&3 \end{bmatrix}+2\begin{bmatrix}2&4 \end{bmatrix}=\begin{bmatrix}5&11 \end{bmatrix}$

但可以发现的是结果之间进行转置就能相互得到

①$(AB)^T=B^TA^T$（列向量转行向量，左乘变右乘）

②$(A^T)^T=A$

③$(A+B)^T=A^T+B^T$（分配律）

matrix matrix_transf(matrix a){
	//作用：矩阵转置A^T
	matrix r;
	matrix_null(&r,a.col,a.row);
	for(int i = 0;i < r.row;i++){
		for(int j = 0;j < r.col;j++){
			r.base[i][j] = a.base[j][i];
		}
	}
	return r;
}

行向量与列向量

如果是以行向量的角度来看，矩阵乘法要为左乘

如果是以列向量的角度来看，矩阵乘法要为右乘

bool matrix_ifcol(matrix a,int j){
	//作用：判断a矩阵是否有第j列 
	return (i >= 0 && i < a.col) ? true : false;
}

void matrix_cadd(matrix a,int j1,int j2){
	//作用：j1列加j2列
	if(!matrix_ifcol(a,j1) || !matrix_ifrow(a,j2)){
		printf("错误：超出列数");
		exit(-1);
	} 
	for(int i = 0;i < a.row;i++){
		a.base[i][j1] = fraction_add(a.base[i][j1],a.base[i][j2]);
	}
	return;
}

void matrix_creplace(matrix a,int j1,int j2){
	//作用：交换j1列、j2列
	if(!matrix_ifcol(a,j1) || !matrix_ifcol(a,j2)){
		printf("错误：超出列数");
		exit(-1);
	} 
	for(int i = 0;i < a.row;i++){
		Fraction t = a.base[i][j1];
		a.base[i][j1] = a.base[i][j2];
		a.base[i][j2] = t;
	}
	return;
}

void matrix_ccmul(matrix a,int j,Fraction C){
	//作用：j列乘上分数C
	if(!matrix_ifcol(a,j)){
		printf("错误：超出列数");
		exit(-1);
	} 
	for(int i = 0;i < a.row;i++){
		a.base[i][j] = fraction_mul(a.base[i][j],C);
	}
	return;
}

void matrix_ccadd(matrix a,int j1,Fraction C,int j2){
	//作用：j1列加C倍的j2列
	if(!matrix_ifcol(a,j1) || !matrix_ifcol(a,j2)){
		printf("错误：超出列数");
		exit(-1);
	} 
	for(int i = 0;i < a.row;i++){
		a.base[i][j1] = fraction_add(a.base[i][j1],fraction_mul(a.base[i][j2],C));
	}
	return;
}

对称矩阵

若$A^T=A$则称矩阵$A$为对称矩阵

①$AA^T$一定也为对称矩阵

逆矩阵

类似倒数概念，若$AA^{-1}=I$

那么$A^{-1}$就叫$A$的"逆矩阵"（或$A$叫$A^{-1}$的"逆矩阵"）

形式上若$A$是$m×n$，那么$A^{-1}$是$n×m$的，这样才能得到单位矩阵

但为了更简单地讨论，在逆矩阵的定义中$A$、$A^{-1}$必须是方阵

若$A$不是方阵，那么$A$的逆被称为广义逆

从线性变换角度上相当于撤销操作。比如用放缩矩阵进行了放缩，如果要将这个操作还原就要用到逆矩阵

奇异矩阵

（0没有倒数，自然矩阵中也存在没有逆的情况）

如果矩阵$A$是可逆的（有其逆矩阵），那么就称$A$是非奇异矩阵（可逆矩阵）

如果矩阵$A$是不可逆的（没有其逆矩阵），那么就称$A$是奇异矩阵（不可逆矩阵）

逆矩阵性质

①$AA^{-1}=I_m$

②$(A^{-1})^{-1}=A$

③$(AB)^{-1}=B^{-1}A^{-1}$

④$(A^T)^{-1}=(A^{-1})^T$

如果$A$是可逆矩阵，则满足

①$A$有$n$个主元

②$Ax=0$仅有平凡解

③$A$的各个列向量是线性无关的

④$b∈R^n$，则矩阵方程$Ax=b$至少有一个解

⑤$A$的各个列向量生成了空间$R^n$

⑥$A^T$也是可逆的

⑦逆矩阵行/列等价于单位矩阵

⑧逆矩阵可以看成是原矩阵的逆向线性变换

求解逆矩阵

将$A^{-1}$看作未知数，相当于求矩阵方程$\begin{bmatrix} A&I \end{bmatrix}$

然后左乘$A^{-1}$，矩阵方程行等价于$\begin{bmatrix}I&A^{-1} \end{bmatrix}$

根据方程只需要将$A$通过行初等变换得到$I$，同时$I$进行相同的变换就能得到逆矩阵

如果是用行向量的角度来看就是求解$\begin{bmatrix}A \\ I \end{bmatrix}$

现在来写代码求解

这里对之前的高斯消元法进行扩展，使得也能求得逆矩阵

#define all 0
#define left 1
#define right 2

typedef int mode;

void matrix_mode(matrix* r,int col,mode code){
	if(code == all){
		return;
	}else if(code == left){
		r->col -= col;
		return;
	}else if(code == right){
		matrix new;
		matrix_null(&new,r->row,r->col-col);
		for(int i = 0;i < new.row;i++){
			for(int j = 0;j < new.col;j++){
				new.base[i][j] = r->base[i][j+col];
			}
		}
		*r = new;
		return;
	}else{
		printf("错误：无效模式码");
		exit(-1);
	}
}

bool matrix_REF_select(matrix a,int* posx,int* posy){
    //作用：REF算法的第一步——选择主元
	int maxx = *posx;
	for(int i = *posx;i < a.row;i++){
		if(fraction_abscmp(a.base[maxx][*posy],a.base[i][*posy]) < 0)maxx = i;
	}
    if(a.base[maxx][*posy]->numerator == 0){
        return false;
    }
    matrix_rreplace(a,*posx,maxx);
    return true;
}

void matrix_REF_eliminate(matrix a,int* posx,int* posy){
	//作用：REF算法中的第二步——主元列除主元以外其他变为0
	for(int i = *posx+1;i < a.row;i++){
		matrix_rcadd(a,i,fraction_div(a.base[i][*posy],fraction_opposite(a.base[*posx][*posy])),*posx);
    }
    return;
}

bool matrix_REF_iterator(matrix a,bool ifsuccess,int* posx,int* posy){
    //作用：REF算法的最后一步——迭代，移动当前位置
	(ifsuccess == true) ? (*posx)++,(*posy)++ : (*posy)++ ;
    if(*posx >= a.row || *posy >= a.col-1)return false;
	else return true;
}

matrix matrix_REF(matrix a,matrix b,mode code){
    //作用：求增广矩阵的阶梯形矩阵
	matrix r = matrix_rowcombine(a,b);
	int posx = 0,posy = 0;
    bool flag;
	do{
        bool issuccess = matrix_REF_select(r,&posx,&posy);
        if(issuccess)matrix_REF_eliminate(r,&posx,&posy);
        flag =  matrix_REF_iterator(r,issuccess,&posx,&posy);
    }while(flag);
	matrix_mode(&r,a.col,code);
    return r;
}

void matrix_REFF_extra(matrix a,int* posx,int* posy){
	//REF算法额外的一步——当前主元变为1主元列其余元素化为0
    matrix_rmul(a,*posx,fraction_create(a.base[*posx][*posy]->denominator,a.base[*posx][*posy]->numerator));
    for(int i = (*posx)-1;i >= 0;i--){
    	matrix_rcadd(a,i,fraction_opposite(a.base[i][*posy]),*posx);
	}
}

matrix matrix_REFF(matrix a,matrix b,mode code){
    //作用：求增广矩阵的简化阶梯形
	matrix r = matrix_rowcombine(a,b);
	int posx = 0,posy = 0;
    bool flag;
	do{
        bool issuccess = matrix_REF_select(r,&posx,&posy);
        if(issuccess){
			matrix_REF_eliminate(r,&posx,&posy);
			matrix_REFF_extra(r,&posx,&posy);
		}
        flag =  matrix_REF_iterator(r,issuccess,&posx,&posy);
    }while(flag);
	matrix_mode(&r,a.col,code);
    return r;
}

matrix matrix_inverse(matrix a){
	if(a.col != a.row){
		printf("错误：行列不匹配");
		exit(-1);
	}
	matrix i;
	matrix_identity(&i,a.row);
	return matrix_REFF(a,i,right);
}

初等矩阵E

初等矩阵是对单位矩阵进行一次初等变换的矩阵

初等矩阵用$E$表示

初等矩阵本身是初等变换得到的，但初等矩阵乘上某一矩阵$A$对$A$也具有同样的初等变换效果

比如$E=\begin{bmatrix}1&0&0 \\ 0&1&0 \\ -4 &0&1 \end{bmatrix}$，$EA$则是$A$将第一行倍加至第三行，如果是$AE$则是将第三列倍加至第一列

这样就有了对矩阵进行初等行/列变换的方法

①左乘$E$为初等行变换，右乘$E$为初等列变换

②初等矩阵或可逆矩阵进行有限次乘积也必然是非奇异矩阵

③任何一个非奇异矩阵可以拆解成有限次初等矩阵的乘积

$A=E_pE_{p-1}...E_1$

④初等矩阵的逆矩阵是一个同类型的初等矩阵

LU分解

LU分解常常用在稀疏矩阵中求解矩阵方程

LU分解是上面第三条的观点

假设存在一个$m×n$的矩阵$A$，那么存在等式

$(∏_iE_i)A=U$（$U$为$A$行等价的阶梯形）

而$E_i$只能通过倍加变换得到的

那么$A=(∏_iE_i)^{-1}U$

其中$(∏_iE_i)^{-1}$被称为置换下三角矩阵，记作$L$

这种仅用倍加变换处理得到的$LU$就称为LU分解

性质

①$A=LU$

②$L$为$min(m,n)×min(m,n)$的方阵

③$L$表明了一种行/列变换的一种过程

比如$L=\begin{bmatrix}1&& \\ -2&1& \\ 1&-3&1 \end{bmatrix}$从行变换角度来说可以将$A$依次进行变换$row_2+2row_1 \\ row_3-row_1 \\ row_3+3row_2$（之所以要加负号是因为$U=L^{-1}A$）

满足此$L$的矩阵有$\begin{bmatrix}2&4&-1&5 \\ -4&-5&3&-8 \\ 2&-5&-4&1 \end{bmatrix}$

依次进行变换后得到$\begin{bmatrix}2&4&-1&5 \\ 0&3&1&2 \\ 0&0&0&2 \end{bmatrix}$

可以发现正是一个阶梯形$U$

病态矩阵

计算机计算时常常会出现微小误差，如果一个矩阵因为微小误差结果就出现了重大变化，就称这类矩阵为病态矩阵。比如奇异矩阵可能因为误差得到的是非奇异矩阵的结果，而一个非常接近奇异矩阵的非奇异矩阵可能因为误差得到的是奇异矩阵的结果

分块矩阵

之前一直是将实数看成矩阵的元素，当然矩阵也可以看成是一个元素

$\left[\begin{array}{c|c|c} \begin{matrix}3&0&-1 \\ -5&2&4 \\ -8&-6&3 \end{matrix}& \begin{matrix}5&9 \\ 0&-3 \end{matrix} & \begin{matrix}-2 \\ 1 \end{matrix} \\ \hline \begin{matrix}-8&-6&3 \end{matrix} & \begin{matrix}1&7 \end{matrix} &-4 \end{array} \right]$

抽象后为

$\begin{bmatrix}A_{11}&A_{12}&A_{13} \\ A_{21}&A_{22}&A_{23} \end{bmatrix}$

分块矩阵的引入是为了更加系统地描述某一模型

比如可以分割称$2×3$的系统，每一系统都有一定的参数

这常常用来将一些高阶矩阵化为低阶矩阵，然后解决

分块矩阵运算

①加法、标量乘法

这和原来的一样，只要保证$A$、$B$维数一样且分块方式一样，则可以进行加法、标量乘法。然后再分块逐个计算

②矩阵乘法AB

除了保证A的列数与B的行数一致以外，还要保证分块后A的列数和B的行数一致

$A$是列数为5，$B$的行数为5

则按照某种分块方式

$A$分成了2列3列，那么$B$也要分成2行3行

$A=\begin{bmatrix}A_{11}&A_{12} \\ A_{21}&A_{22} \end{bmatrix}$，$B=\begin{bmatrix}B_1 \\ B_2 \end{bmatrix}$

$AB=\begin{bmatrix}A_{11}B_1+A_{12}B_2 \\ A_{21}B1+A_{22}B_2 \end{bmatrix}$

依据分块矩阵可以这样定义矩阵乘法

$row_i(A)$为$A$的第$i$行的分块，$col_i(A)$为A的第$i$列的分块

$AB=\begin{bmatrix}col_1(A)&col_2(A)&...&col_n(A) \end{bmatrix} \begin{bmatrix}row_1(B) \\ row_2(B) \\ \vdots \\row_n(B) \end{bmatrix} =∑_i~col_i(A)row_i(B)$

③转置

分块矩阵的逆运算，出了矩阵元素要转置以外，本身的矩阵也要转置

$\begin{bmatrix}A_{11}&A_{12} \\ A_{21}&A_{22} \end{bmatrix}^T=\begin{bmatrix}(A_{11})^T&(A_{21})^T \\ (A_{12})^T&(A_{22})^T \end{bmatrix}$

六、行列式

点击查看详细内容

意义（口胡）

行列式是一个多项式函数，用来描述当前维度的空间大小

用$det~~A$或$|A|$表示，其中$A$是当前空间的矩阵

当前空间大小如何度量？

显然空间是无穷大的，但空间又是有大有小的（比如放缩矩阵）

于是用基向量平行后所围成的图像来度量空间大小

比如$\begin{bmatrix}1&0 \\ 0&1 \end{bmatrix}$其基向量是$\begin{bmatrix}1 \\ 0 \end{bmatrix}$和$\begin{bmatrix}0 \\ 1 \end{bmatrix}$

在二维情况下是基向量平行后是平行四边形，也就说平行四边形的面积来描述当前空间的大小

$det~\begin{bmatrix}1&0 \\0&1 \end{bmatrix}=1$

在二维下行列式的公式比较简单

$det~\begin{bmatrix}a&b \\ c&d \end{bmatrix}=ad-bc$

$det~\begin{bmatrix}2&4 \\0&3 \end{bmatrix}=底×高=2×3=6$

还有一种说法是行列式表示的是当前空间和原空间大小的比值。但原空间大小是1，当前空间大小和线性变换后的空间大小当然是一样的，因此也行列式$det$也可以看成是一个空间进行线性变换后与原空间大小的比值

如果$n$阶方阵$A$是非奇异矩阵，对于$R^n$内的$∀b$，方程$Ax=b$只有唯一解

同时左乘$A^{-1}$

$AA^{-1}x=A^{-1}b→x=A^{-1}b$

当然如果一个矩阵方程是右乘$xA=b$

那么$x=bA^{-1}$

虽然能用逆矩阵求解方程组，但一般情况是直接用高斯消元法或分解

三阶以下的行列式

$det~[a] = a$

$det~\begin{bmatrix}a&b \\c&d \end{bmatrix}=ad-bc$

$det~\begin{bmatrix}a_{11}&a_{12}&a_{13} \\ a_{21}&a_{22}&a_{23} \\a_{31}&a_{32}&a_{33} \end{bmatrix}=a_{11}a_{22}a_{33}+a_{12}a_{23}a_{31}+a_{13}a_{21}a_{32}-a_{11}a_{23}a_{32}-a_{12}a_{21}a_{33}-a_{13}a_{22}a_{21}$

可以将三阶行列式化简

$a_{11}a_{22}a_{33}+a_{12}a_{23}a_{31}+a_{13}a_{21}a_{32}-a_{11}a_{23}a_{32}-a_{12}a_{21}a_{33}-a_{13}a_{22}a_{21} \ $$=a_{11}(a_{22}a_{33}-a_{23}a_{32})-a_{12}(a_{21}a_{33})+a_{13}(a_{21}a_{32}-a_{22}a_{31})$

$=a_{11}det~~\begin{bmatrix}a_{22}&a_{23} \\a_{32}&a_{33} \end{bmatrix}-a_{12}det~~\begin{bmatrix}a_{21}&a_{23} \\a_{31}&a_{33} \end{bmatrix}+a_{13}det~~\begin{bmatrix}a_{21}&a_{22} \\a_{31}&a_{32} \end{bmatrix}$

进行抽象

$=a_{11}det~~A_{11}-a_{12}det~~A_{12}+a_{13}det~~A_{13}$

其中$A_{ij}$的行标列标和$a_{ij}$是一致的

而矩阵$A_{ij}$是划去$i$行$j$列所剩下的矩阵

n阶行列式

形式上将$n$阶矩阵变成$(n-1)$阶矩阵

这是一个递归定义

$det~~A=a_{11}det~~A_{11}-a_{12}det~~A_{12}+...+(-1)^{1+n}a_{1n}det~~A_{1n}$

$=∑_{j=1}^n(-1)^{1+j}a_{1j}det~~A_{1j}$

而$A_{1j}$也可以再次通过定义降一阶，直到三阶、二阶这种熟悉地行列式时就能得到答案

用不太标准的程序算法就是

det(matrix A){
	//判断基准情况
    int sum = 0;
    for(int i = 1;i <= n;i++){
        sum += (-1)^(1+i)a[1][i]det(A[1][i]);
    }
    return sum;
}
//不过这个算法实现

其中$A_{ij}$被称为$a_{ij}$的余子式

其中$C_{ij}=(-1)^{i+j}A_{ij}$被称为$a_{ij}$的代数余子式

行列式的展开有两种，按行展开或按列展开

可以在任意列任意行展开

$det~~A=∑_{j=1}^na_{ij}C_{ij}$

$det~~A=∑_{i=1}^na_{ij}C_{ij}$

至于行列式某一项的正负号有两种方法确定

①定义

②棋盘模式

代数余子式的正负取决于$a_ij$的位置，可以用一个棋盘来表示当前代数余子式的正负

$\begin{bmatrix}+&-&+&... \\ -&+&-&\\ +&-&+& \\ \vdots&&& \ddots \end{bmatrix}$

逆序数下行列式的定义

一组n个元素组成的有序数组被称为n级排列

而在n级排列中如果一个数大于之后的一个数就称为这两个数构成逆序

逆序数是指一个n级排列中拟序的总数，用$τ(i_1,i_2...i_n)$表示

逆序数为奇数的排列称为奇排列，逆序数为偶数的排列称为偶排列

行列式的定义还可以写成

$det~~A=∑_{j_{1}...j_{n}}(-1)^{τ(j_{1}...j_{n})a_{1j_{1}}}a_{1j_{2}}...a_{1j_{n}}$

逆序数还揭示了一点：n阶行列式展开后项数有$n!$项

这种定义虽然用到了逆序数，但在程序实现上要简单不少，但实现上依然复杂，不采用这种定义实现

性质

①如果A是三角矩阵，那么$det~~A$为主对角线各个元素之积

②初等变换对$det~~A$的影响

倍加：$det~~A_{倍加}=det~~A$

倍乘：$det~~A_{倍乘k}=k~det~~A$

交换：$det~~A_{某两行/列交换}=-det~~A$

③依据初等变换倍加、交换可以得到

$det~~A=(-1)^rU$

其中$r$为交换次数，$U$为阶梯形

而一个阶梯形又是上三角矩阵可以通过乘上对角线元素来求得

Fraction matrix_det(matrix a){
	//作用：求矩阵a的行列式
	if(a.col != a.row){
		printf("错误：行列不匹配");
		exit(-1);
	}
	int count = 0;
	int posx = 0,posy = 0;
	bool flag = true;
	while(flag){
		bool issuccess;
		{
			int maxx = posx;
			for(int i = posx;i < a.row;i++){
				if(fraction_abscmp(a.base[maxx][posy],a.base[i][posy]) < 0)maxx = i;
			}
			if(a.base[maxx][posy]->numerator == 0){
				issuccess = false;
			}else{
				issuccess = true;
			}
			if(maxx != posx){
				matrix_rreplace(a,posx,maxx);
				count++;
			}
		}
		if(issuccess){
			matrix_REF_eliminate(a,&posx,&posy);
		}
		flag =  matrix_REF_poschange(a,issuccess,&posx,&posy);
	}
	Fraction r;
	r = (count%2) ? fraction_create(-1,1) : fraction_create(1,1);
	for(int i = 0;i < a.row;i++){
		r  = fraction_mul(r,a.base[i][i]);
	}
	return r;
}

④若$det~~A≠0$，则方阵$A$是非奇异矩阵矩阵

若$det~~A=0$，则方阵$A$是奇异矩阵

//求逆矩阵算法中可以增加这一条件
if(matrix_det(a) == 0){
		printf("错误：奇异矩阵");
		exit(-1);
}

⑤$det~~A^T=det~~A$

⑥$det~~AB=det~~A.det~~B$

（一般情况$det~~(A+B)≠det~~A+det~~B$）

⑦线性性质

分为两种，从列向量观点来看，假设$A$中某一列为$x$

则存在函数$T(x)=\begin{bmatrix}a_1&...&x&a_n \end{bmatrix}$

满足$T(cx)=c~T(x)$和$T(x+y)=T(x)+T(y)$

对于行向量也是如此

⑧初等矩阵行列式性质

$det~~E=\begin{cases}~~~1，E_{倍加} \\ -1，E_{交换} \\ ~~~k，E_{倍乘k} \end{cases}$

⑨$det^{-1}~~A=det~~A^{-1}$（可以从$det~~I=det~~AA^{-1}$得到）

⑩$det~~A^{k}=det^{k}~~A$（包括$k<0$的情况）

⑪$det~~kA=k^ndet~~A$

⑫若某一行/列元素相同，则$det~~A=0$

⑬若某一行/列与另一行/列成比例，则$det~~A=0$

范德蒙行列式（略）

形如$det~~\begin{bmatrix}1&1&...&1 \\ x_1&x_2&...&x_n \\ \vdots & \vdots && \vdots \\ x_1^{n-1}&x_2^{n-1}&...&x_n^{n-1} \end{bmatrix}$称为n阶范德蒙行列式

这里不做证明，结果为$∏_{1≤j≤i≤n}(x_i-x_j)$

余子式与代数余子式的性质（略）

因为$C_{ij}=(-1)^{i+j}A_{ij}$，所以代数余子式和余子式之间可以相互转换，最多差个负号

如果求某一矩阵的余子式相加或代数余子式相加，可以转换成行列式

比如求$A_{11}+2A_{12}+4A_{14}$可以将矩阵$A$中$a_{11}$、$a_{12}$、$a_{14}$元素改成1、2、4然后这个新矩阵的行列式就是$A_{11}+2A_{12}+4A_{14}$的结果

根据范德蒙行列式，还可以知道

$a_{1i}A_{1j}+a_{2i}A_{2j}...+a_{ni}A_{nj}=0(i≠j)$

$a_{i1}A_{j1}+a_{i2}A_{j2}...+a_{ni}A_{nj}=0(i≠j)$

克拉默法则

假设$A=\begin{bmatrix}a_1&a_2&...&a_n \end{bmatrix}$

那么定义

$A_i(b)=A.I_i(x)=\begin{bmatrix}Ae_1&...&Ax&...Ae_n \end{bmatrix}$

$=\begin{bmatrix}a_1&a_2&...&b(位于i列)&...&a_n \end{bmatrix}$

$A_i(b)$是将矩阵$A$第$i$列替换为$b$

如果$A$是可逆的$n$阶矩阵，那么矩阵方程$Ax=b$的解可以表示为

$det~~A.det~~I_i(x)=det~~A_i(b)$

得 $I_i(x)=x_i=\frac{det~~A_i(b)}{det~~A}$，$i=1,2...n$

利用克拉默法则不考虑算法复杂度的情况下，逻辑上是要比高斯消元法还要简单的一种求解线性方程组的方法

逆矩阵的公式

如果已知$n$阶矩阵$A$，求其逆矩阵本质上是解矩阵方程$Ax=I_n$

根据克拉默法则

可以求$Ax=e_j$，$j$为单位矩阵第$j$列

$x_{ij}=\frac{det~~A_i(e_j)}{det~~A}$求解的是第$i$行第$j$列的逆矩阵的元素

综上$A^{-1}=\begin{bmatrix}\frac{det~~A_1(e_1)}{det~~A}&\frac{det~~A_1(e_2)}{det~~A}&...&\frac{det~~A_1(e_n)}{det~~A} \\ \frac{det~~A_2(e_1)}{det~~A}&\frac{det~~A_2(e_2)}{det~~A}&...&\frac{det~~A_2(e_n)}{det~~A} \\ \vdots& \vdots&& \vdots \\ \frac{det~~A_n(e_1)}{det~~A}&\frac{det~~A_n(e_2)}{det~~A}&...&\frac{det~~A_n(e_n)}{det~~A} \end{bmatrix}$

提取$\frac{1}{det~~A}$

$A^{-1}=\frac{1}{det~~A} \begin{bmatrix}det~~A_1(e_1)&det~~A_1(e_2)&...&det~~A_1(e_n) \\ det~~A_2(e_1)&det~~A_2(e_2)&...&det~~A_2(e_n) \\ \vdots& \vdots&& \vdots \\ det~~A_n(e_1)&det~~A_n(e_2)&...&det~~A_n(e_n)\end{bmatrix}$

现在处理$det~~A_i(e_j)$，首先这个矩阵表示在第$i$列被$e_j$替换，而要知道$e_j$中只有第$j$个元素是1，其余是0。

因此矩阵在第$i$列中，除了$(j,i)$为1以外，都为0

$det~~A_i(e_j)=(-1)^{i+j}det~~A_{ji}=C_{ji}$

因此$A^{-1}=\frac{1}{det~~A}\begin{bmatrix}C_{11}&C_{21}&...&C_{n1} \\ C_{12}&C_{22}&...&C_{n2} \\ \vdots& \vdots && \vdots \\ C_{1n} & C_{2n} &...&C_{nn} \end{bmatrix}$

而其中右边的余因子矩阵的转置被称为$A$的伴随矩阵，记作$adj~~A$

$A^{-1}=\frac{1}{det~~A}adj~~A$

这个公式俨然不适合计算，但作为理论揭示了一些内容（比如空间大小上，逆矩阵的行列式和矩阵的行列式成反比）

也说明判断矩阵是否可逆关键看$det~~A$是否为0

【注：部分术语可能与其他材料不同，$M_{ij}$表示余子式，$A_{ij}$表示代数余子式，$A^*$表示伴随矩阵】

反对角线行列式公式（口胡）

做题时发现的一个问题，除了课本中的公式，鄙人自行推出了另一个公式，程序中测试了1~5000阶来验证公式，未发现错误

有证明，但不严谨，这里就不说明了

大概思路：生成序列$\{0,1,1,0,0,1,1,0,0,...\}$

$原公式：D=(-1)^{\frac{n(n-1)}{2}}∏_i λ_i$

新公式：$D=(-1)^{1-⌈\frac{n+1}{2}⌉ \% 2 }∏_i λ_i$

等价公式1$D=(-1)^{1-⌈\frac{n+1}{2}⌉ + (n+1)//2 }∏_i λ_i$（$//$表示整除）

和群友讨论时，有人说$\frac{n+1}{2}$在计算机计算时会出现浮点数，有缺点，于是我稍微变换了一下

等价公式2：$D=(-1)^{1-((n+1)//2+(n+1) \%2) \% 2 }∏_i λ_i$

新公式最大的问题是形式复杂

但等价公式2解决了新公式的浮点数问题以及原公式的溢出问题

七、向量空间

点击查看详细内容

在线代中有一个相当重要的问题，那就是在空间上具有什么含义

行/列向量

用$n×1$的矩阵来代表一个列向量，其中$n$表示这个列向量在空间的维数

比如$\begin{bmatrix}1 \\ 2 \\ 3 \end{bmatrix}$是表示在三维空间中$(1,2,3)$的向量，当然默认始点在原点，那么这个列向量也可以代表是三维空间的一个点

从另外一个观点来看，也可以用一个$1×n$的矩阵表示一个行向量

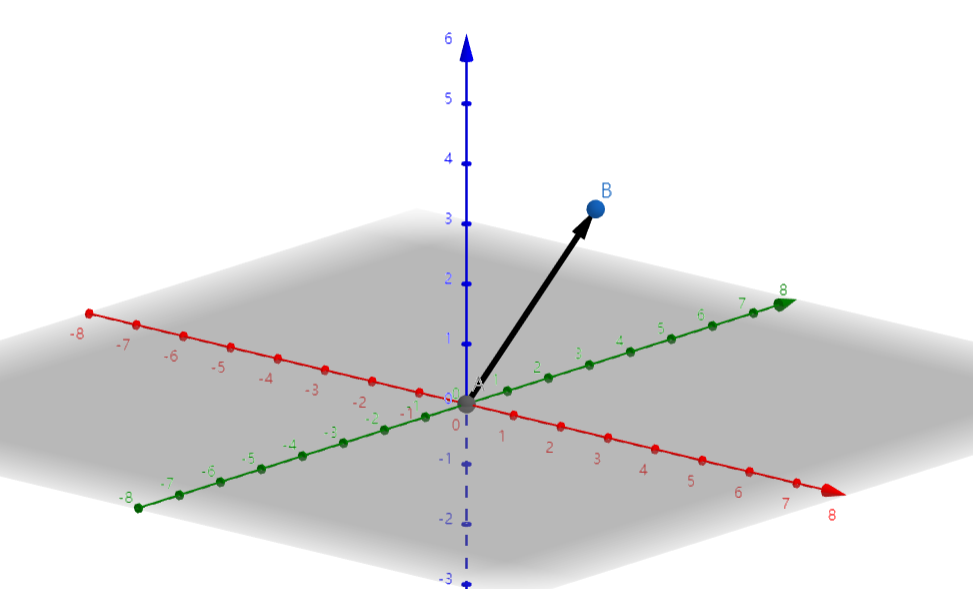
基于列向量的运算

①标量乘法

若$\vec u=\begin{bmatrix}u_1 \\... \\ u_n \end{bmatrix}$

$c\vec u=\begin{bmatrix}c.u_1 \\... \\ c.u_n \end{bmatrix}$

②加法

若$\vec u=\begin{bmatrix}u_1 \\... \\ u_n \end{bmatrix}$若$\vec v=\begin{bmatrix}v_1 \\... \\ v_n \end{bmatrix}$

$\vec u~ +~ \vec v = \begin{bmatrix}u_1+v_1 \\... \\ u_n+v_n \end{bmatrix}$

③两个向量的线性组合

若$\vec u=\begin{bmatrix}u_1 \\... \\ u_n \end{bmatrix}$若$\vec v=\begin{bmatrix}v_1 \\... \\ v_n \end{bmatrix}$

$c_1.\vec u~ +~c_2. \vec v = \begin{bmatrix}c_1.u_1+c_2.v_1 \\... \\ c_1.u_n+c_2.v_n \end{bmatrix}$

行向量也同理

线性组合与向量方程

通过线性组合得到的向量设为$\vec y$

这样得到的一个方程称为向量方程

$c_1 \vec {v_1}+c_2 \vec {v_2}...+c_n \vec {v_n} = \vec y$

其中$c_i$称为权，$\vec{v_i}$为列向量，$\vec y$是通过线性组合后得到的新向量

其中这一组向量组成一个集合，记作$β$，称为向量集

$R^n$空间（略）

线代中的空间满足三个性质

假设$H⊆R^n$

(1) $0∈H$

(2) $u+v∈H$

(3) $Cu∈H$

矩阵$A$各个列向量构成的空间称为列空间，记作$Col~~A={b~|~~b=Ax,x∈R^n}$

矩阵$A$各个行向量构成的空间称为行空间，记作$Row~~A={b~|~~b=xA,x∈R^n}$

$Ax=0$所有解的集合称为$A$的零空间，记作$Nul~~A={x~|~~Ax=0,x∈R^n}$

假设向量集$β$线性无关，就称$β$是线性无关集

向量集$β$生成的空间记作$Span(β)$，称为张成空间或生成空间

不同形式下的方程

这是线性方程组

$\begin{cases}v_{00}c_1+v_{01}c_2...+v_{0n}c_n=y_0 \\ v_{10}c_1+v_{11}c_2...+v_{1n}c_n=y_1 \\... \\v_{n0}c_1+v_{n1}c_2...+v_{nn}c_n=y_n \end{cases}$

这是增广矩阵

$\begin{bmatrix}v_{00}&v_{01}&...&v_{0n}&y_0 \\v_{10}&v_{11}&...&v_{1n}&y_1\\...&...&...&...&...\\v_{n0}&v_{n1}&...&v_{nn}&y_n \end{bmatrix}$

这是向量方程

$c_0 \vec {v_0}+c_1 \vec {v_1}...+c_n \vec {v_n}=∑_0^n c_i.\vec {v_i} = \vec y$

这是矩阵方程

$Ax=b$

结论：线性方程组、增广矩阵、向量方程、矩阵方程可以随意转换，这个结论是显然的，是从不同角度或抽象而来的

齐次线性方程组

矩阵方程$Ax=b$中若$b=\mathbf 0$则称这是齐次的，否则为非齐次的

（注：这里的$\mathbf 0$是表示一个零矩阵）

其中如果计算出来的解$x=\mathbf 0$则称这个解是平凡解

结论

①若齐次线性方程组$Ax=\mathbf 0$有非平凡解，则这个方程至少有1个自由变量，即有无数解

②设矩阵$A$是$m×n$的矩阵，则下列命题要么全满足要么全不满足

■$∀b$取$R^m$空间内的任意点，$Ax=b$一定相容

■$b$可以看成是$A$各列向量的线性组合

■由$A$各个列向量生成的$R^m$空间一定是$n$维空间

■$A$每一行都有一个主元

③齐次线性方程组和非齐次线性方程组的关系：

设方程为$Ax=b$，那么$Ax=\mathbf 0$的解仅仅是忽略了$Ax=b$解的常数项

（注：若Ax=b只有唯一解，则解都是常数项，则Ax=0的解忽略常数项后就是0）

③若$v_1...v_p$在空间$V$中，则$Span(v_1...v_p)⊆V$

线性相关性

假设存在向量集$β$，若向量方程$β_1x_1+β_2x_2...+β_nx_n=0$存在非平凡解，则称向量集$β$具有线性相关性

反之，若向量方程仅存在非平凡解，则称向量集$β$具有线性无关性且称$β$是线性无关集

而某一矩阵$A$从列/行向量角度来看就是向量集

①具有线性相关性的向量集存在$v$是其他向量的线性组合

②线性无关集$β$的张成空间$H=Span(β)$而$H$恰好是$|β|$维的空间

③生成集定理

具有线性相关性的向量集$α$中如果去掉可以线性组合得到的向量，那么剩下的向量也就构成了线性无关集$β$，张成空间$H$恰好是$|β|$维的。

那么去除的向量对于张成空间不做任何贡献，可以认为是冗余的

$H=Span(α)=Span(β)$，$β⊆α$

④从空间角度来说，某一空间$H$的一组基向量就是某一线性无关集

Nul A和Col A的性质

假设有一$m×n$的矩阵$A$

①$Nul~~A⊆R^n$

②$Col~~A⊆R^m$

③$|Nul~A|$为$A$自由变量个数

④若$Nul~A={0}$的充要条件是$Ax=0$仅有平凡解

⑤若$Col~A=R^m$的充要条件是$Ax=b$仅有唯一解

⑥对矩阵初等变换不影响矩阵的线性关系

假如存在一个$m×n$的矩阵$A$，那么可以将$A$通过高斯消元变为$U$

然后根据$U$的自由变量数，即非主元的个数来得到$ |Nul~A|$

根据$U$的绑定变量数，即主元的个数来得到$|Col~A|$

同时$U$中非主元列全部去除即可得到$A$张成空间的基向量

⑦线性无关集$β$从生成空间角度来看，是一个"不大不小"的向量集。如果加入一个新向量很可能会使得$β$具有线性相关性或者使得空间新增一维，如果减少一个向量则会让空间失去一维，无法得到原本空间

坐标系（略）

如果某空间$H$可以通过基$β$生成得到，那么这一基$β$各个向量也称为坐标系的基向量

基是指线性无关集

①唯一表示定理：若有空间$H$的基$β={b_1...b_n}$，则$∀x∈H$，$x=c_1b_1+...+c_nb_n$（这个等式唯一）

其中$\begin{bmatrix}c_1 \\ \vdots \\ c_n \end{bmatrix}$记作$[x]_β$称为$x$的$β-$坐标向量

$x=[x]_β.β$

维数（略）

维数的概念是从线性相关性、线性无关性推导得出的，一般情况在判断维数时需要先判断是否线性相关

在空间中维数表示相互独立即线性无关的一组向量，显然线性基$β$生成空间的维数为$|β|$

若空间$H$是由有限线性无关集生成的，则维数为有限维，记作$dim~~H$

若空间$H$是由无限线性无关集生成，则维数为无穷维

维数为$n$的空间被称为$n$维空间

①若有$n$维空间$H$是由向量集$β$生成的，则满足$n≤|β|$

推论：若$|β|＞n$，则$β$一定是线性相关的

②$n$维空间所有可能的基的元素数也为$n$

③基定理：若有$n$维空间$H$，则具有$n$个元素数的线性无关集一定是$H$的基

③$dim~~R^n=n$

④若有限维空间$H⊆V$，则$dim~~H≤dim~~V$

⑤$dim~~Nul~~A$为$A$中自由变量的个数

⑥$dim~~Col~~A$为$A$中主元列的个数

⑦$dim~~Row~~A$为$A$中非零行的个数

这里阐述了行空间、列空间、零空间的维数定义，而在下面秩的概念中将表明行空间、列空间、零空间维数之间的关系

秩

$m×n$的矩阵$A$中从行空间和列空间两种不同角度去考虑

将$A$化简为某一阶梯形$U$

假设这个阶梯形$U$形式上是这样的$\begin{bmatrix}■&※&※&※&※ \\ &■&※&※&※ \\ &&&■&※ \\ & \end{bmatrix}$

那么这里列空间维数就是主元列个数（即主元个数）为3

行空间的基为$\{\begin{bmatrix}■&※&※&※&※ \end{bmatrix},\begin{bmatrix}0&■&※&※&※ \end{bmatrix},\begin{bmatrix}0&0&0&■&※ \end{bmatrix}\}$

行空间维数就是非零行个数（即主元个数）为3

列空间的基为$\{\begin{bmatrix}■ \\ 0 \\ 0 \\ 0 \end{bmatrix},\begin{bmatrix}※ \\ ■ \\ 0 \\ 0 \end{bmatrix},\begin{bmatrix}※ \\ ※ \\ ■ \\ 0 \end{bmatrix}\}$

可见列空间维数和行空间维数都取决于主元，因为主元所在列为主元列，主元所在行为非零行，所以能得出$dim~~Col~~A=dim~~Row~~A$

而这个主元数就称之为秩数，用$rank~~A$表示

从定义上得出以下结论

①$rank~~A=dim~~Col~~A=dim~~Row~~A$

②$dim~~Col~~A$为$A$主元个数即绑定变量个数

③$dim~~Row~~A$为$A$主元个数即绑定变量个数

④秩定理：$dim~~Nul~~A+rank~~A=n$

⑤秩定理推论：秩数就是矩阵的绑定变量数，零空间维数就是矩阵的自由变量数

秩的概念揭示了行空间、列空间、零空间之间维数的关系，这种关系我认为也是刻画了矩阵方程$Ax=b$、$xA=b$以及$Ax=0$的关系

int matrix_dim(matrix a,space code){
	/*code若为col，计算矩阵a列空间维数
	  code若为row，计算矩阵a行空间维数
	  code若为nul，计算矩阵a零空间维数
	  code若为rank，计算矩阵a秩数*/
	//bug:使用dim函数后a会变成阶梯形
	int bind = 0;
	matrix r = a;

	int posx = 0,posy = 0;
    bool flag = true;
	while(flag){
        bool issuccess = matrix_REF_select(r,&posx,&posy);
        if(issuccess)matrix_REF_eliminate(r,&posx,&posy);
        (issuccess) ? posx++,posy++,bind++ : posy++;
    	if(posx >= r.row || posy > r.col-1)flag = false;
		else flag = true;
    }
	return (code == space_nul) ? r.col-bind : bind;
}

基本原理也是高斯消元，bind变量用来计数绑定变量数，然后利用秩定理可以求得零空间维数

但秩数同样受到行数和列数限制，比如一个$6×9$的矩阵是不可能有2维零空间。

如果具有2维零空间，那么秩数就为7，但$dim~~Row~~A$因为行数限制是不可能超过6的，因此不具有2维零空间

注：一般情况而言，会将$A$的主元列作为$Col~~A$的基，会将$U$的非零行作为$Row~~A$的基

注：n维度不代表空间$R^n$

秩和逆矩阵

若$A$是$n$阶逆矩阵，则满足以下充要条件

①$Col~~A=R^n$

②$rank~~A=n$

③$dim~~Nul~~A=0$

（部分和转置相关定理由于课本并未给出，这里不会详细说明）

$rank~~A=rank~~A^T$

$Row~~A=Col~~A^T$

$rank~~A+dim~~Nul~~A^T=m$

课本中对于秩的定义

课本中采用行列式进行定义

在$m×n$的矩阵中任取$k$行$k$列然后取出做$det$运算，这个就称为$A$的$k$阶子式

存在$A$的$n$阶子式不为0，而所有$n+1$阶子式为0，那么这个$n$就是$A$的秩数

形象点说就是在$A$的$k$维下如果有不为0的，就代表A的列/行空间在当前$k$维里是能度量的，如果在$k+1$维下所有行列式都为0，那么就代表列/行空间在$k+1$维下是无法度量的（比如空间是一维的线，在二维里问线的面积是多少）那么这个$k$就是秩数了

从这个定义看，秩数是$A$能度量的最大维度

①若$A$的秩数为$r$，那么$r$阶子式就称为$A$的最高阶非零子式（不唯一）

②$m×n$的矩阵$A$，其行空间维数、列空间维数受行数、列数制约

$\begin{cases}dim~~Col~~A ≤ m~~~∧~~~dim~~Col~~A ≤ n \\ dim~~Row~~A ≤ m~~~∧~~~dim~~Row~~A ≤ n \\ rank~~A ≤ m~~~∧~~~rank~~A ≤ n \end{cases}$

③$m×n$的矩阵$A$

若$rank~~A=m$，则$A$称为行满秩矩阵

若$rank~~A=n$，则$A$称为列满秩矩阵

若同时满足上面两点，即$A$为方阵且$rank~~A=n$，则$A$称为满秩矩阵

若$A$为方阵但$rank~~A≠n$，则$A$称为降秩矩阵

④根据逆矩阵和秩的定理，满秩矩阵为非奇异矩阵，降秩矩阵为奇异矩阵

向量与秩（略）

不管是列向量集还是行向量集都能组成一个矩阵，从而能得出向量和秩的关系

①$m$个$n$维向量，若$m>n$，则向量集线性相关

②若向量集$\{a_1,...a_m\}$可由向量集$\{b_1...b_n\}$线性表出（线性组合）且$m>n$

则向量集$\{a_1,...a_m\}$线性相关

③若向量集$\{a_1,...a_m\}$可由向量集$\{b_1...b_n\}$线性表出且$\{a_1,...a_m\}$线性相关

则$m≤n$

④极大无关组$β$：$β$为向量组$α$的一部分且$α$可由$β$线性表出，则$β$称为极大无关组

⑤极大无关组与原本向量组等价$Span(α)=Span(β)$

⑥同一向量组的极大无关组等价

⑦等价的极大无关组秩数一样

⑧行秩即为行空间的维数，列秩即为列空间的维数。行秩等于列秩

齐次线性方程组的基础解系（略）

将方程$Ax=0$化成向量集Ω，这个向量集就称为是$Ax=0$的基础解系

基变换

基变换也就是线性变换的原理

假设基$β$，那么在$β$为基的情况$[x]_β$为$β-$坐标向量，满足等式$x=β[x]_β$

假若现在要线性变换，将基从$β$变为$c$，那么就要将$[x]_β$变为$[x]_c$

$[x]_c=[β[x]_β]_c=[[b_1]_c~[b_2]_c~...[b_n]_c][x]_β$

其中$[[b_1]_c~[b_2]_c~...[b_n]_c]$记为$P_{c←β}$

$[x]_c=P_{c←β}[x]_β$

①$(P_{c←β})^{-1}[x]_c=[x]_β$即$(P_{c←β})^{-1}=P_{β←c}$

只要求出$P_{c←β}$就能得出$[x]_c$

根据定义得出方程组$\begin{cases}b_1=c[b_1]_c \\ b_2=c[b_2]_c \\ \dots \\ b_n=c[b_n]_c \end{cases}$

这里以$\{~[b_1]_c~~~...~~~[b_n]_c~\}$为变量$x$，$cx=β$，$x=c^{-1}β$

$P_{c←β}=x=c^{-1}β$

因此$[x]_c=c^{-1}β[x]_β$

比如某向量$x$通过左乘$A$，得到$Ax$

这在基变换中相当于$x$左乘$β^{-1}$，得到$[x]_β=β^{-1}x$

如果要从$Ax$左乘B，得到$BAx$

这在基变换中相当于$β^{-1}x$左乘$c^{-1}$，得到$[x]_c=c^{-1}[x]_β=c^{-1}β^{-1}x$

在此例中$A=β^{-1}$，$B=c^{-1}$

八、特征值、特征向量

点击查看详细内容

在之前线性变换描述了$x$和$Ax$之间的区别，从行列式描述大小区别，伴随矩阵描述“方向”区别，空间描述基、坐标系的区别 #### 特征值、特征向量

若存在$λ$使$Ax=λx$（$A$为方阵，$x≠0$）成立

则称$λ$为$A$的特征值

称$x$为$A$对应于$λ$的特征向量

经变换可得$(A-λI)x=0$

其中$x$解集为$A-λI$的零空间，这个空间也称为$A$对应于$λ$的特征空间

(1)若特征方程成立，则方程存在非平凡解，即$r(A-λI)＜n$即$det~~(A-λI)=0$

(2)若$A$为三角矩阵，则$λ$为主对角线元素

(3)若$A$存在零特征值，则该矩阵为奇异矩阵，否则为非奇异矩阵

(4)矩阵的一组特征值构成的集合称为谱，若谱中不同的特征值对应了任意一个特征向量，则这些特征向量构成的向量集$V$具有线性无关性

(5)$A^kx=λ^kx$

特征方程

$det~~(A-λI)=0$称为特征方程

特征方程展开后称为特征多项式，即$det~~(A-λI)=∏(λ_i-λ)$

根据特征方程求出的根也称为特征根

特征根若存在$x$个相同的值，则称为该特征值重数为$x$，该特征根也称为重根

若考虑重根、复数根，则$n$阶矩阵有且仅有$n$个特征值

若已知某一特征根$λ$，则求$(A-λI)x=0$的基础解系后便能求得特征向量

特征向量表明伸缩变换后方向固定的向量

(1)$det~~(A-λI)=∏(λ_i-λ)$

(2)$det~~A=∏λ_i$

(3)$A^{-1}$的特征值为$λ^{-1}$，即$A^{-1}x=λ^{-1}x$

(4)$A^T$的特征值为$λ$，即$A^Tx=λx$

(5)$A^{k}$的特征值为$λ^{k}$，即$A^{k}x=λ^{k}x$

(6)$λ_i$所对应的特征空间维数小于等于其重数$x$

矩阵相似

若满足$A=PBP^{-1}$（$P$可逆），则称$A$与$B$相似

若矩阵相似满足以下关系

(1)具有相同特征方程

(2)具有相同特征多项式

(3)具有相同行列式

(4)具有相同迹

(5)若$A$,$B$相似，则$kA$,$kB$相似

(6)若$A$,$B$相似，则$A^{-1}$,$B^{-1}$相似

对角化（谱分解）

若存在$A=PDP^{-1}$（$D$为对角矩阵）

则称$A$可对角化，从$A$到$PDP^{-1}$的过程称为对角化或谱分解

(1)对角化定理：$n$阶矩阵$A$可对角化的充要条件是：$A$存在着一组具有线性无关性的$n$个特征向量

可推得其他充要条件：⇔所有相异特征值$λ_i$所对应特征空间的维数之和为$n$，$∑dim(A-λ_iI)=n$

⇔所有相异特征值$λ_i$特征空间的维数等于其重数$x$，$dim(A-λ_iI)=x$

(2)$A^k=PD^kP^{-1}$

(3)具有$n$个不同特征值的$n$阶矩阵一定可对角化

(4)$n$阶对称矩阵一定可对角化

对角化（谱分解）步骤

1.求出$A$的谱$λ$

2.根据不同特征值$λ_i$求出对应的线性无关的特征向量$v_i$

3.得出$P=\begin{bmatrix}v_1&v_2&...&v_n \end{bmatrix}$，$D=\begin{bmatrix}λ_1&& \\ &\ddots & \\ && λ_n \end{bmatrix}$

其中$v_i$和$λ_i$对应

九、正交性

点击查看详细内容

范数（长度）

范数表明一个向量的大小

用$||u||$表示

范数为1的向量称为单位向量常用$e$表示

单位化是指将某个向量$u$经过运算得到单位向量，$e_u=\frac{u}{||u||}$

距离

表示两向量之间的范数

$dist(u,v)=||u-v||=\sqrt{||u-v||^2}=\sqrt{∑(u_i-v_i)^2}$

内积

内积是向量与向量之间的一种运算，在原本向量空间中加上内积运算，这个空间九称为内积空间

内积运算有这些写法$u.v$或$<u,v>$或$[u,v]$

满足以下性质

(1)$<u,v>=<v,u>$

(2)$<u+v,w>=<u,w>+<v,w>$

(3)$<cu,v>=c<u,v>$

(4)$<u,u>≥0$且$<u,u>=0⇔u=0$

(5)Cauchy–Schwarz不等式：$|<u,v>|≤||u||+||v||$

范数相关性质

(6)$||u||=\sqrt{<u,u>}$

(7)$||u||^2=<u,u>$

(8)$||cu||=|c|.||u||$

距离相关性质

(9)三角不等式：$||u+v||≤||u||+||v||$

(10)$||u-v||=||u||.||v||.cos~~α$（$cos~~α$为两向量的夹角）

向量的正交性

通俗来讲，正交就是垂直

若满足$||u+v||=||u-v||$，即$<u,v>=0$那么就称$u$和$v$是相互正交的正交向量

记作$u⊥ v$

(1)零向量与任意向量正交

(2)勾股定理：$||u+v||^2=||u||^2+||v||^2$

空间的正交性

假设有空间W和空间V

其中在空间V的任意向量$v_i$若与空间W的任意向量$w_j$正交

那么就称这两个空间是正交的，其中的某一向量也与另一空间正交

空间与空间的正交记作$V=W^⊥$或$W=V^⊥$或$V⊥W$

向量与空间的正交性记作$v_i⊥W$

(1)$Nul~~A=(Row~~A)^⊥$

(2)$Nul~~A^T=(Col~~A)^⊥$

正交集

若集合$V=\{v_1,v_2...v_n\}$其中任意向量之间正交，则称这个集合为正交集

(1)若$V$正交集，则$V$是线性无关集

(2)在正交集构成空间中的某一向量满足

$y=∑c_iy_i$

那么可以求得$c_i=\frac{<y,v_i>}{<v_i,v_i>}$，这个系数是$V$构成向量的一个权值，在后续也会用到

(3)假设$y=αu+z$，其中$u∈L$，$z⊥L$

$⇒z=y-αu$

$∵z⊥u$

$∴<y-αu,u>=0$

$⇒α=\frac{<y,u>}{<u,u>}$

其中$αu$记作$Proj_L~y$表示$y$在空间$L$上的正交投影

（值得注意的是正交投影只存在于空间$L$）

那么可得$Proj_L~y = \frac{<y,u>}{<u,u>} u$

正交分解定理

和上述第三点性质类似，但推广到了更抽象的空间

$y=z_1+z_2$，$z_1∈W$，$z2⊥W$

其中$z2$所在空间恰好是$W^⊥$

可以得知$y$存在于$W$空间和$W^⊥$空间

可以将$y$分解为$z1∈W$和$z2∈W^⊥$

而$W$和$W^⊥$的设置是任意的

$z1$就称为$y$在$W$的投影

$z1=∑ \frac{<y,u_i>}{<u_i,u_i>}u_i$

$∴y=Proj_W~y+z_2$（$Proj_W~y⊥z_2$）

最佳逼近定理

$||y-Proj_W~y||~<~||y-v||$（$v∈W$，$v≠Proj_W~y$）

最佳逼近定理表明已知空间$W$，那么距离$y$最近的向量是$Proj_W~y$

（单位）正交基

单位化的正交基称为单位正交基

满足性质$U^TU=I$

$\begin{bmatrix}u_1^T \\ \vdots \\ u_n^T \end{bmatrix} \begin{bmatrix}u_1&...&u_n \end{bmatrix}=\begin{bmatrix}u_1^Tu_1&...&u_1^Tu_n \\ \vdots & \ddots & \vdots \\ u_n^Tu_1 & ... &u_n^Tu_n \end{bmatrix}=I$

（$u_i^Tu_j= \begin{cases}1，i＝j \\ 0，i≠j \end{cases}$

单位正交基在线性映射下依然保持范数、正交性

(1)$||Ux||=||x||$

(2)$<Ux,Uy>=<x,y>$

(3)$<x,y>=0~~⇔~~<Ux,Uy>=0$

(4)$||U||=\sqrt{U^TU}=1$

(5)正交矩阵$U$若为方阵，则行列均是正交的

(6)在正交基下，$Proj_W~y=∑(<y,u_i>)u_i=UU^Ty$

Gram-Schmidt正交化算法

已知线性无关集$X=\{x_1,x_2...x_n\}$是子空间$W$的基

可以通过以下步骤构造正交基$V=\{v_1,v_2...v_n\}$

(1)$v_1=x_1$，$W_1=Span(v_1)$

(2)$v_i=x_i-∑ \frac{<x_i,v_i>}{v_i,v_i}v_i$，$W_i=Span(v_1...v_n)$

可看作$v_i=x_i-Proj_{W_{i-1}}~~x_i$

即$x_i$剔除$W_{i-1}$的空间分量

即可求出正交基

若需要单位正交基

还需要进行一步单位化

$e_{v_i}=\frac{v_i}{||v_i||}$

QR分解

$A=QR$（$A$为$m×n$矩阵）

$Q$是由$Col~~A$标准正交基形成的$m×n$矩阵

$R$是$n×n$上三角可逆矩阵，主对角线元素均为正数

$x_i=r_iv_i$

$r_i=\begin{bmatrix}r_{1i} \\ \vdots \\ r_{ii} \\ 0 \\ \vdots \\ 0 \end{bmatrix}$

QR分解步骤

(1)求出正交矩阵$Q$

(2)$R=Q^{-1}A=Q^TA$求出$R$

十、二次型

点击查看详细内容

对称矩阵

若$A$为对称矩阵，则不同特征空间之间的任意特征向量均是具有正交性

$v_i⊥v-j$，$v_i∈V_i$，$v_j∈V_j$

矩阵关系

相等关系：$A=B$，不仅形式一样，元素也要相同

等价关系：$A=PBQ$，即通过任意次初等变换可得到则称为等价

相似关系：$A=P^{-1}BP$，即矩阵可逆

合同关系：$A=C^TBC$，即实矩阵对称

(1)具有合同关系的矩阵一定也具有相似关系、等价关系

(2)具有相似关系的矩阵一定也具有等价关系

(3)$A$可正交对角化的充要条件是：$A$是对称矩阵

谱定理

若$A$为$n$阶对称矩阵，则

(1)$A$具有$n$个实特征值且一定重复

(2)每一特征空间维数等于其重数，即$dim~~(A-λI)=x$

(3)特征空间之间相互正交，即$V_i⊥V_j$

(4)可正交对角化

二次型矩阵

$Q(x)=x^TAx$（$A$为对称矩阵）称为二次型

对称矩阵$A$的元素$a_ij$表示二次型某一项为$a_{ij}x_ix_j$

若二次型展开中$i≠j$，那么对应于对称矩阵的$a_{ij}$也需要折半

主轴定理

主轴定理核心原理是变量代换

$x=Py$

$x^TAx=y^T(P^{-1}AP)y$

如果能将$x^TAx$变换为$y^TDy$就称为二次型标准化

其中$P$称为主轴

主轴的作用是将二次型原本非标准位置转变为标准位置，即改变基向量将基向量变为$I$

二次型标准化步骤

(1)求解$A$的特征向量集$P$（线性无关且可逆）

(2)令$x=Py$求解$y$

(3)求得$x^TAx=y^T(P^TAP)y=y^TDy$（$D$与$P$相对应）

二次型类型

正定二次型：$x≠0$且$∀x~~~Q(x)>0$

半正定二次型：$∀x~~~Q(x)≥0$

负定二次型：$x≠0$且$∀x~~~Q(x)>0$

半负定二次型：$∀x~~~Q(x)≤0$

不定二次型：$∃x~~~Q(x)>0~~~∨~~~Q(x)<0$

判定定理：

若$A$为对称矩阵

■ $Q(x)$正定的充要条件是：$A$的特征值均为正数

■ $Q(x)$负定的充要条件是：$A$的特征值均为负数

■ $Q(x)$不定的充要条件是：$A$的特征值有正数也有负数

Last、实际应用

点击查看详细内容

①列向量标量乘法

假设列向量为要生产的一个商品$\vec u=\begin{bmatrix}材料成本=0.8 \\ 人力成本=1.2 \\ 管理成本=0.5\end{bmatrix}$

那么生产一百个商品成本为$100\vec u=\begin{bmatrix}80\\120\\50 \end{bmatrix}$

注：列向量可以设置不同参数表示某一个具象或抽象的东西，而标量乘法代表多个东西下的总参数

②构造线性模型：求解线性方程组

这个应用极其广泛，大部分学科都需要求解线性方程组，这里就简单列举化学方程式配平

配平化学式$KMnO_4+HCl→KCl+MnCl_2+Cl_2+H_2O$

根据化学式的要求，首先系数必须是整数，要保证左右相等

用一列表示某一分子含有的元素数

$\begin{bmatrix}K \\ Mn \\ O \\ H \\ Cl \end{bmatrix}$

这个方程即为$x_1 \begin{bmatrix}1\\1\\4\\0\\0 \end{bmatrix}+x_2 \begin{bmatrix}0\\0\\0\\1\\1 \end{bmatrix}=x_3 \begin{bmatrix}1\\0\\0\\0\\1 \end{bmatrix}+x_4 \begin{bmatrix}0\\1\\0\\0\\2 \end{bmatrix}+x_5 \begin{bmatrix}0\\0\\0\\0\\2 \end{bmatrix}+x_6 \begin{bmatrix}0\\0\\1\\2\\0 \end{bmatrix}$

即为$\begin{bmatrix}1&0&-1&0&0&0\\1&0&0&-1&0&0 \\ 4&0&0&0&0&-1 \\0&1&0&0&0&-2 \\ 0&1&-1&-2&-2&0 \end{bmatrix}\begin{bmatrix}x_1 \\x_2 \\x_3 \\x_4 \\ x_5 \\ x_6 \end{bmatrix} = \begin{bmatrix}0 \\ 0 \\ 0 \\ 0 \\ 0 \end{bmatrix}$

然后求解增广矩阵$\begin{bmatrix}1&0&-1&0&0&0&0\\1&0&0&-1&0&0&0 \\ 4&0&0&0&0&-1&0 \\0&1&0&0&0&-2&0 \\ 0&1&-1&-2&-2&0&0 \end{bmatrix}$即可

求出来为$\begin{bmatrix}1&0&0&0&0&-\frac{1}{4}&0 \\ 0&1&0&0&0&-2&0 \\ 0&0&1&0&0&-\frac{1}{4}&0 \\0&0&0&1&0&-\frac{1}{4}&0 \\ 0&0&0&0&1&-\frac{5}{8}&0 \end{bmatrix}$

即$\begin{cases}x_1 = -1/4 \\ x_2=-2 \\ x_3 = -1/4 \\ x_4 = -1/4 \\ x_5 = -5/8 \end{cases}$

然后去掉分母和负数就能求得$\begin{cases}x_1 = 2 \\ x_2=16 \\ x_3 = 2 \\ x_4 = 2 \\ x_5 = 5 \end{cases}$

因此这个化学式配平后为$2KMnO_4+16HCl→2KCl2MnCl_2+2Cl_2+5H_2O$

在中学阶段是凭感觉配平，现在可以很快速地用线性代数来配平

除了化学方程式配平以外，只要你能意识到当前所做的运算是在求解线性方程组就能用线性代数求解

在实际应用过程中需要注意以下特点

①需要注意每一行每一列所代表的实际含义，比如这里每一行代表不同元素数，每一列代表当前分子

②需要注意解的取值范围，需要对结果进行适当变换，比如化学式配平只能取正整数

注：比较特殊的线性方程组是差分方程

③图像学中的应用（略）

见第六节，三维很多变换我省略了，这些在网上是能找到的，这篇blog不侧重图像学的应用，因此省略了

④列昂惕夫投入产出模型（略）

假设经济体系分为3个部门，x为产出，d为需求

消耗\部门	A	B	C
A	0.5	0.4	0.2
B	0.2	0.3	0.1
C	0.1	0.1	0.3

此表格为不同部门生产需要消耗其他部门资源的数量

这个表格用矩阵表示为C，称为消耗矩阵

那么满足等式$x=Cx+d$

参考教程

Geogebra:matrix 3D
Geogebra:Geometry of 2x2 Matrix Multiplication with Intro Questions

参考书籍

《线性代数及其应用(第三版)》，David C.Lay/

posted on 2021-09-02 09:32 摸鱼鱼的尛善阅读(818) 评论(1) 编辑收藏举报

会员力量，点亮园子希望

刷新页面返回顶部

线性代数——C语言实现（超长篇慎入）【存在问题，不建议看】

线性代数

镇楼图

仅作为学习线代的实验，不会特别注重内存泄漏、bug等问题

目前不打算用写稀疏矩阵，之后可能会转C++

〇、准备工作（构建分数ADT）

一、线性方程(组)

线性方程

解

线性方程组

增广矩阵

初等变换

行阶梯形矩阵

行阶梯形矩阵

简化阶梯形矩阵(U)

二、高斯消元法（行化简算法）

①构建框架

②选择主元

②消元

③迭代

④汇总

⑤阶梯形矩阵变简化阶梯形矩阵

三、线性方程组的解

存在与唯一性定理

四、线性变换

标准矩阵

①平移变换

②旋转变换

③对称变换

④伸缩变换

⑤剪切变换

⑥投影变换

五、矩阵运算性质

基本术语

标量乘法、加法

矩阵乘法

\(AB\)是\(A\)的各列乘上\(B\)所对应的权

\((AB)_{ij}=∑_{k=0}^{n}a_{ik}b_{kj}\)

乘幂

转置

行向量与列向量

对称矩阵

逆矩阵

奇异矩阵

逆矩阵性质

求解逆矩阵

初等矩阵E

LU分解

病态矩阵

分块矩阵

分块矩阵运算

六、行列式

意义（口胡）

三阶以下的行列式

n阶行列式

逆序数下行列式的定义

性质

范德蒙行列式（略）

余子式与代数余子式的性质（略）

克拉默法则

逆矩阵的公式

反对角线行列式公式（口胡）

七、向量空间

行/列向量

基于列向量的运算

线性组合与向量方程

\(R^n\)空间（略）

不同形式下的方程

齐次线性方程组

结论

线性相关性

Nul A和Col A的性质

坐标系（略）

维数（略）

秩

秩和逆矩阵

课本中对于秩的定义

相关结论

向量与秩（略）

齐次线性方程组的基础解系（略）