深度优先遍历

利用深度优先遍历 求组合问题 Eg: 1-9 中 任取k个整数 总共有多少种组合？

深度优先遍历很容易列出所有可能 这里我们分情况 标注几个易错的点

不重复组合

不重复组合 则表明 如果我们取K=3（取N1、N2、N3） 则N1从1-9中任取 但N1需要排除N1 同理N3需要排除N1、N2

代码如下

 public static void DFS3(int start,  List<int> nums, List<IList<int>> ret)
        {
            if (nums.Count > gK )
                return;
            if (gK == nums.Count )
            {
                ret.Add(new List<int>(nums));
                return;
            }
            for (int i = start; i < 10; i++)
            {
                
                nums.Add(i);
                DFS3(++start,  nums, ret);
                //++start（start在开始N3遍历前自增 N2处记录start=3） : N1=1,N2=2,N3  当N3>9 遍历完 返回N2的遍历 此时i++ N2=3开始遍历  N3则是=++start=4开始遍历
                //start+1 （start在开始N3遍历后+1 N2处记录start=2） : N1=1,N2=2,N3  当N3>9 遍历完 返回N2的遍历 此时i++ N2=3开始遍历  N3则是=++start=3开始遍历
                nums.RemoveAt(nums.Count - 1);
            }
        }

【注】这里有个易错点 就是递归时start的传值 一定要是 ++start

++start 组合结果如下

而start+1结果则是

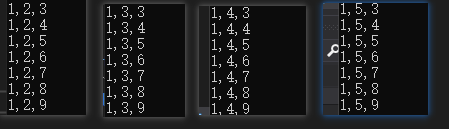
可重复组合 即全排列 则N1、N2、N3均有9种可能

public static void DFS3(int start,  List<int> nums, List<IList<int>> ret)
        {
            if (nums.Count > gK )
                return;
            if (gK == nums.Count )
            {
                ret.Add(new List<int>(nums));
                return;
            }
            for (int i = start; i < 10; i++)
            {
                
                nums.Add(i);
                DFS3(1,  nums, ret);
                nums.RemoveAt(nums.Count - 1);
            }
        }