bzoj1001 [ICPC-Beijing 2006]狼抓兔子

我满心以为本题正解为最短路，结果到处都是最大流……

几乎所有的都写了什么“对偶图”跑最短路，但我真的不知道什么叫做对偶图
-------------------------------------------------------------------------------------------------
介绍一下本题的最短路算法叭。并不算难。主要是感性理解。

 

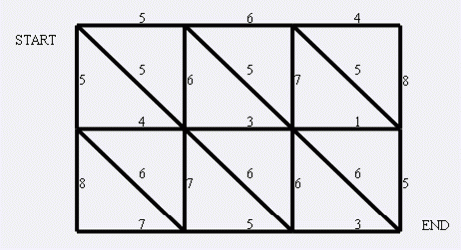
首先很容易观察出这是一个最小割，那么就是求最大流了。

但是这题的点数高达10e6，按常理来说最大流应该稳稳地TLE。但是没有T好气哦

那么想办法！

首先最小割在本题时可以这样感性理解：上图是一个你同学在钢铁厂打出来的一个铁架子。你把start处用手捏起来，end处自然垂下。用一个剪刀钳把这个铁架子拦腰剪成两半。

如果剪成好几瓣（掉下来有好几个联通块的），那么显而易见，不如剪成两半（把刚才几个剪断的地方原样拼起来变成两个联通块）。

我们把三角形看成是点，黑色的边看成是连接三角形的边，那么剪成两半的意思是……在三角形点的图上找一条从左下到右上的最短路径！沿着这条路径剪开就行了。

但是这题的点数高达10e6，按常理来说SPFA应该稳稳地TLE。但是没有T好气哦

那就堆优化dijkstra。

这个加边超烦的。但思路清晰的话就没什么问题。记得在左下空白处设一个源点，右上角设一个汇点。源点连接所有邻接它的左边的、下边的三角形点，汇点连接所有邻接它的右边的、上边的三角形点。

#include <cstdio>
#include <queue>
using namespace std;
const int N=1002,S=N*N*6+30,inf=(1<<30)-1;
int n,m,a[N][N],b[N][N],c[N][N],d[S],id[N][N],ss,tt,h[S],v[S],nx[S],w[S],eg=1;
bool vis[S]={0};
struct info
{
    int x,w;
}data;
inline bool operator<(const info &a,const info &b)
{
    return a.w>b.w;
}
priority_queue<struct info> pq;
inline void egadd(int uu,int vv,int ww)
{
    nx[++eg]=h[uu];h[uu]=eg;
    v[eg]=vv;w[eg]=ww;
}
void rd(int &s)
{
    s=0;char c=getchar();
    while (c<48) c=getchar();
    while (c>=48) s=(s<<1)+(s<<3)+(c^48),c=getchar();
}
int main()
{
    scanf("%d%d",&n,&m);
    for (int i=1;i<=n;i++)
        for (int j=1;j<=m-1;j++)
            rd(a[i][j]);
    for (int i=1;i<=n-1;i++)
        for (int j=1;j<=m;j++)
            rd(b[i][j]);
    for (int i=1;i<=n-1;i++)
        for (int j=1;j<=m-1;j++)
            rd(c[i][j]);
    n--;m--;
    if (!n)
    {
        int res=inf;
        for (int i=1;i<=m;i++)
            if (a[1][i]<res)
                res=a[1][i];
        printf("%d",res);
        return 0;
    }
    if (!m)
    {
        int res=inf;
        for (int i=1;i<=n;i++)
            if (b[i][1]<res)
                res=b[i][1];
        printf("%d",res);
        return 0;
    }
    for (int i=1;i<=n;i++)
        for (int j=1;j<=m;j++)
            id[i][j]=(i-1)*2*m+j;
    ss=n*2*m+1;tt=ss+1;
    for (int i=1;i<=n;i++)
        for (int j=1;j<=m;j++)
        {
            egadd(id[i][j],id[i][j]+m,c[i][j]);
            egadd(id[i][j]+m,id[i][j],c[i][j]);
        }
    for (int i=1;i<=n;i++)
        for (int j=1;j<=m-1;j++)
        {
            egadd(id[i][j],id[i][j+1]+m,b[i][j+1]);
            egadd(id[i][j+1]+m,id[i][j],b[i][j+1]);
        }
    for (int i=1;i<=n-1;i++)
        for (int j=1;j<=m;j++)
        {
            egadd(id[i][j]+m,id[i+1][j],a[i+1][j]);
            egadd(id[i+1][j],id[i][j]+m,a[i+1][j]);
        }
    for (int i=1;i<=m;i++)
    {
        egadd(id[1][i],tt,a[1][i]);
        egadd(ss,id[n][i]+m,a[n+1][i]);
    }
    for (int i=1;i<=n;i++)
    {
        egadd(ss,id[i][1]+m,b[i][1]);
        egadd(id[i][m],tt,b[i][m+1]);
    }
    for (int i=1;i<=tt;i++)
        d[i]=inf;
    d[ss]=0;
    pq.push((info){ss,0});
    while (!pq.empty())
    {
        while (!pq.empty() && vis[pq.top().x])
            pq.pop();
        if (pq.empty()) break;
        data=pq.top();
        pq.pop();
        int x=data.x,ww=data.w;
        printf("%d %d\n",x,ww);
        vis[x]=true;
        for (int i=h[x];i;i=nx[i])
            if (!vis[v[i]] && d[v[i]]>ww+w[i])
            {
                d[v[i]]=ww+w[i];
                pq.push((info){v[i],d[v[i]]});
                printf("Add:%d %d\n",v[i],d[v[i]]);
            }
    }
    printf("%d",d[tt]);
    return 0;
}