基本算法

算法定义

　　一个计算过程，解决问题的方法
　　有输入有输出，给规定的输入得到规定的输出

时间复杂度

　　用来估计算法运行时间的一个式子（单位）
　　一般来说，时间复杂度高的算法比复杂度低的算法慢。
　　常见复杂度效率排序

　　　　　　O(1)<O(logn)<O(n)

简单的判断时间复杂度？（无递归）

　　循环减半的过程---->O(logn)

　　几层循环就是n的几次方的复杂度

空间复杂度

　　用来估计算法内存占用大小的式子

列表查找：从列表中查找指定元素

　　输入：列表、待查找元素

　　输出：元素下标或者未查到元素　　

1 li = [1, 5, 6, 55, 64]
2 res = 6 in li
3 li.index(6)

顺序查找线性查找 O(n)

　　从列表第一和元素开始，顺序进行搜索，直到找到为止。　　

1 for i in li:
2     pass

二分查找 O(logn)

　　从有序列表的候选区data[0:n]开始，通过对待查找的值与候选区中中间值的比较，可以使候选区减少一半。

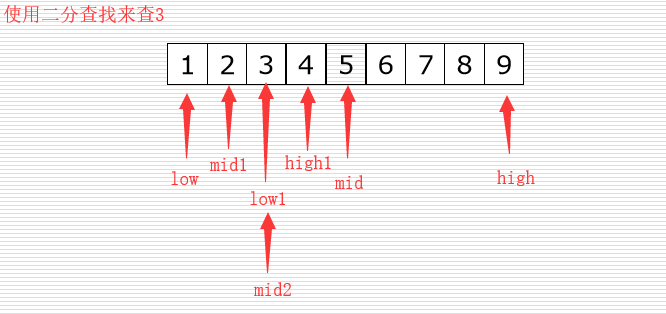
从上图：

　若low <= high 存在候选区
　若low > high 不存在候选区说明被查找的值根本不存在

 1 #!/usr/bin/env python
 2 # -*- coding:utf-8 -*-
 3 
 4 
 5 def bin_search(li, val):
 6     low = 0
 7     high = len(li) - 1
 8     while low <= high:
 9         # 存在候选区
10         mid = (low + high) // 2
11         if li[mid] == val:
12             return mid
13         elif li[mid] < val:
14             # 右边
15             low = mid + 1
16         else:
17             # 左边
18             high = mid - 1
19     # 查找不到我默认返回-1
20     return -1
21 
22 
23 # 递归
24 def bin_search_rec(li, val, low, high):
25     if low <= high:
26         mid = (low + high) // 2
27         if li[mid] == val:
28             return mid
29         elif li[mid] > val:
30             return bin_search_rec(li, val, low, mid - 1)
31         else:
32             return bin_search_rec(li, val, mid + 1, high)
33     else:
34         return -1

low B三人组(时间O(n**2) 空间O(1))

冒泡排序 O(n**2)

思路：相邻两位置比较大小

 1 # 装饰器
 2 def timer(func):
 3     def wrapper(*args, **kwargs):
 4         import time
 5         start_time = time.time()
 6         res = func(*args, **kwargs)
 7         stop_time = time.time()
 8         print('运行时间%s' % (stop_time - start_time))
 9         return res
10     return wrapper

 1 @timer
 2 def bubble_sort(li):
 3     for i in range(len(li)-1):  # i表示第n趟 一共n或者n-1趟
 4         exchange = False
 5         for j in range(len(li)-i-1):  # 第i趟 无序区[0， n-i-1] j表示箭头0~n-i-2
 6             if li[j] > li[j+1]:
 7                 li[j], li[j+1] = li[j+1], li[j]
 8                 exchange = True
 9         if not exchange:
10             break

选择排序O(n**2)

思路：一趟遍历记录最小的数，放到第一个位置，一直循环

 1 def get_min_pos(li):
 2     """
 3     找最小值的位置
 4     :param li:
 5     :return:
 6     """
 7     min_pos = 0
 8     for i in range(1, len(li)):
 9         if li[i] < li[min_pos]:
10             min_pos = i
11     return min_pos
12 
13 
14 @timer
15 def select_sort(li):
16     for i in range(len(li) - 1):  # n趟或者n-1趟
17         # 第i趟无序区的范围 i~最后
18         min_pos = i   # min_pos更新无序区最小位置
19         for j in range(i+1, len(li)):
20             if li[j] < li[min_pos]:
21                 min_pos = j
22         li[i], li[min_pos] = li[min_pos], li[i]

插入排序O(n**2)

思路：摸到的牌与前边的牌进行逐个比较

 1 @timer
 2 def insert_sort(li):
 3     for i in range(1, len(li)):  # i表示摸到的牌下标
 4         tmp = li[i]   # 摸到的牌
 5         j = i - 1
 6         while j >= 0 and li[j] > tmp:  # 只要往后挪就循环 2个条件都得满足
 7             # 如果j=-1停止挪动 如果li[j]小了 停止挪动
 8             li[j+1] = li[j]
 9             j -= 1
10         li[j+1] = tmp
11 
12 
13 # li = list(range(10000))
14 # random.shuffle(li)
15 # insert_sort(li)

NB排序三人组

快排O(nlogn)

思路：
　　1.取一个元素p,使p归位
　　2.列表被P分成两部分，左边都比P小，右边都比P大
　　3.递归完成排序

 1 #!/usr/bin/env python
 2 # -*- coding:utf-8 -*-
 3 
 4 import sys
 5 import random
 6 from lowB import timer
 7 # 快排 O(n*logn)
 8 
 9 
10 @timer
11 def quick_sort(li):
12     _quick_sort(li, 0, len(li)-1)
13 
14 
15 # 这种写法没从新开辟新的空间
16 def _quick_sort(li, left, right):
17     if left < right:
18         mid = partition(li, left, right)
19         _quick_sort(li, left, mid-1)
20         _quick_sort(li, mid+1, right)
21 
22 
23 def partition(li, left, right):
24     tmp = li[left]
25     while left < right:
26         while left < right and li[right] >= tmp:
27             right -= 1
28         li[left] = li[right]
29         while left < right and li[left] <= tmp:
30             left += 1
31         li[right] = li[left]
32     li[left] = tmp
33     return left
34 
35 
36 @timer
37 def sys_sort(li):
38     li.sort()
39 
40 
41 li = list(range(10000))
42 random.shuffle(li)
43 quick_sort(li)  # 运行时间0.19099831581115723
44 sys_sort(li)    # 运行时间0.0009989738464355469   Python内部排序快100倍
45 
46 # sys.setrecursionlimit(2000)设置递归深度
47 
48 
49 # 开辟了新的空间 列表生成式 生成两列表占空间 思想完全相同
50 def quick_sort2(li):
51     if len(li) < 2:
52         return li
53     tmp = li[0]
54     left = [v for v in li[1:] if v <= tmp]
55     right = [v for v in li[1:] if v > tmp]
56     left = quick_sort2(left)
57     right = quick_sort2(right)
58     return left + [tmp] + right

问题：1.当列表全部倒序递归的层数就非常大 2.如果p元素只有一边有数据和p元素随机取呢

堆排序(O(nlogn))

　插曲了解些数据结构

　树是一种数据结构可以仿照目录结构理解
　树是一种可以递归定义的数据结构
　上张图辅助理解

根节点：A
叶子节点：B/C等等没孩子的节点
树的深度（高度）：4
树的度：6
孩子节点的度：比如节点F，它的度为3
子树：比如：F K L W构成一个子树 E I J P Q也是

　　二叉树：度不超过2的树（节点最多有两个叉）

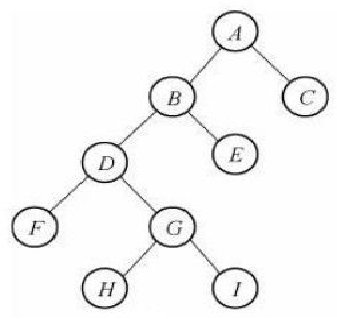
满二叉树：节点全是满的，而且每个节点的孩子节点只能为2个
完全二叉树：最多两个孩子节点，并且是最左边一个个的少

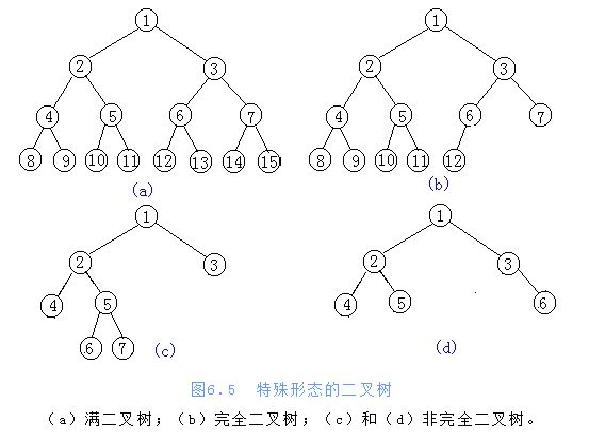
二叉树的存储方式：链式存储、顺序存储方式

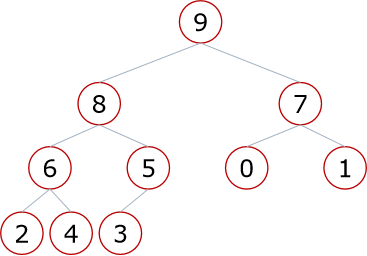
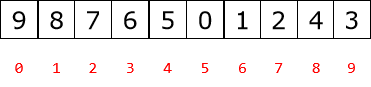
父节点和左孩子节点的编号下标关系：

　　　　0-----1 1-----3 2-----5 3------7 4-----9

　　　　推出关系 i------2i+1

父节点和右孩子节点的编号下标关系

　　　　0------2 1------4 2-----6 3-------8 4-----10

　　　　推出关系 i-------2i+2

孩子与父节点的编号下标关系

　　　　1------0 2------0

　　　　3------1 4------1

　　　　5------2 6------2

　　　　推出关系左:(i-1)/2 右:(i-2)/2

　　　　总体：(i-1)//2

　　堆

大根堆：一棵完全二叉树，满足任意节点都比孩子节点大

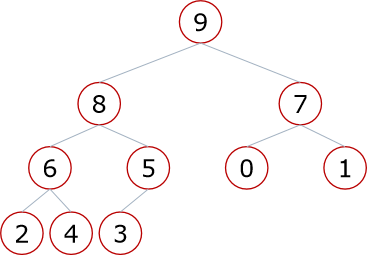
小根堆：一棵完全二叉树，满足任意节点都比孩子节点小

-----------------------------------------------------------------------------------------------------------------------

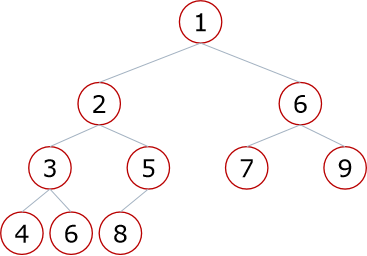
堆排序的三环节：

堆的向下调整环节性质
创建堆（用到性质）
挨个出数（用到性质）

 1 # 堆的向下调整性质
 2 def sift(li, low, high):
 3     # li表示树  low表示树的根 high:表示最后一个子节点的位置
 4     tmp = li[low]
 5     i = low  # 指向空的位置
 6     j = 2 * i + 1  # 指向两孩子的位置
 7     while j <= high:  # 循环退出的第二种情况：j大于high，说明空位i没有孩子了，i是叶子节点
 8         if j + 1 <= high and li[j] < li[j+1]:  # 如果右孩子存在，并且右孩子比左孩子的值大，指向右孩子
 9             j += 1
10         if li[j] > tmp:
11             # 省长上位
12             li[i] = li[j]
13             # 变换i与j的位置
14             i = j
15             j = 2 * i + 1
16         else:  # 循环跳出的第一种情况：j位置的值比tmp小，说明两孩子都比tmp小
17             break
18         li[i] = tmp
19 
20 
21 @timer
22 def heap_sort(li):
23     # 创建堆
24     n = len(li)
25     # 从最后一个子树的位置一个个进行的调整
26     # 最后一个节点的位置是n-1
27     # 孩子节点的父亲孩子节点是i-1 // 2
28     for low in range(n//2-1, -1, -1):
29         sift(li, low, n-1)
30     print(li)  # 画一个堆出来
31     # 挨个出数
32     for high in range(n-1, -1, -1):
33         li[0], li[high] = li[high], li[0]  # 退休 棋子
34         sift(li, 0, high-1)
35 
36 
37 li = list(range(10))
38 random.shuffle(li)
39 heap_sort(li)
40 print(li)

归并排序　　

　归并排序之一次归并假设现在的列表分两段有序，合成一个有序列表

 1 def merge(li, low, mid, high):
 2     i = low   # 是第一段有序列表中第一个元素
 3     j = mid + 1  # 是第二段有序列表的第一个元素
 4     ltmp = []  # 创列表比较之后元素存放
 5     while i <= mid and j <= high:
 6         if li[i] <= li[j]:
 7             ltmp.append(li[i])
 8             i += 1
 9         else:
10             ltmp.append(li[j])
11             j += 1
12     while i <= mid:
13         ltmp.append(li[i])
14         i += 1
15 
16     while j <= high:
17         ltmp.append(li[j])
18         j += 1
19 
20     li[low:high + 1] = ltmp
21     # for i in range(low, high+1):
22     #     li[i] = ltmp[i-low]
23 # li = [2, 5, 7, 8, 9, 1, 3, 4, 6]
24 # merge(li, 0, 4, 8)
25 # print(li)
26 
27 
28 def merge_sort(li, low, high):
29     if low < high:
30         # 分解
31         mid = (low + high) // 2
32         # 递归
33         merge_sort(li, low, mid)
34         merge_sort(li, mid+1, high)
35         # 一次归并
36         merge(li, low, mid, high)
37 
38 
39 li = [10, 4, 6, 3, 8, 2, 5, 7]
40 merge_sort(li, 0, len(li) - 1)
41 print(li)

实例展示不要直接合并起来再sort（nlogn）归并一次合成下面实例就是（n）

 1 #!/usr/bin/env python
 2 # -*- coding:utf-8 -*-
 3 
 4 
 5 # 如果现在两个有序列表 合并成一个
 6 # def merge2list(li1, li2):
 7 #     li = []
 8 #     i = 0
 9 #     j = 0
10 #     while i < len(li1) and j < len(li2):
11 #         if li1[i] <= li2[j]:
12 #             li.append(li1[i])
13 #             i += 1
14 #         else:
15 #             li.append(li2[j])
16 #             j += 1
17 #     while i < len(li1):
18 #         li.append(li1[i])
19 #         i += 1
20 #     while j < len(li2):
21 #         li.append(li2[j])
22 #         j += 1
23 #     return li
24 #
25 #
26 # li1 = [2, 5, 7, 8, 9]
27 # li2 = [1, 3, 4, 6]
28 # li = merge2list(li1, li2)
29 # print(li)

总结：

快速排序 < 归并排序 < 堆排序

三种排序算法的缺点：

　快速排序：极端情况下排序效率低
　归并排序：需要额外的内存开销
　堆排序：在快的排序算法中相对较慢

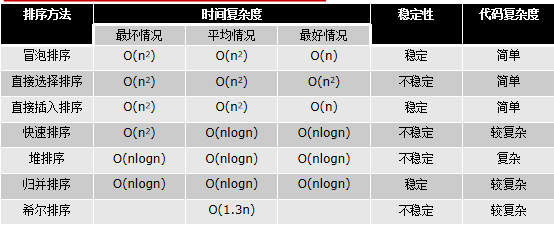
补充：

　　希尔排序

是一种分组插入排序算法。
首先取一个整数d1=n/2，将元素分为d1个组，每组相邻量元素之间距离为d1，在各组内进行直接插入排序；
取第二个整数d2=d1/2，重复上述分组排序过程，直到di=1，即所有元素在同一组内进行直接插入排序。

 1 #!/usr/bin/env python
 2 # -*- coding:utf-8 -*-
 3 
 4 import random
 5 
 6 
 7 def timer(func):
 8     def wrapper(*args, **kwargs):
 9         import time
10         start_time = time.time()
11         res = func(*args, **kwargs)
12         stop_time = time.time()
13         print('运行时间%s' % (stop_time - start_time))
14         return res
15     return wrapper
16 
17 
18 def insert_sort_gap(li, d):
19     for i in range(1, len(li)):
20         tmp = li[i]
21         j = i - d
22         while j >= 0 and li[j] > tmp:
23             li[j+d] = li[j]
24             j -= d
25         li[j+d] = tmp
26 
27 
28 @timer
29 def shell_sort(li):
30     d = len(li) // 2
31     while d > 0:
32         # do something
33         insert_sort_gap(li, d)
34         d = d // 2
35 
36 
37 li = list(range(10000))
38 random.shuffle(li)
39 shell_sort(li)
40 # 运行时间0.11099767684936523
41 # 对插入排序确实提高了很多,但是跟NB三人组还是差距大

计数排序

现在有一个列表，列表中的数范围都在0到100之间，列表长度大约为100万。设计算法在O(n)时间复杂度内将列表进行排序。

 1 #!/usr/bin/env python
 2 # -*- coding:utf-8 -*-
 3 
 4 
 5 # 数字不能很大  这样创列表超级大
 6 def count_sort(li, max_num=50):
 7     count = [0 for _ in range(max_num + 1)]
 8     for val in li:
 9         count[val] += 1
10     li.clear()
11     for i, v in enumerate(count):
12         # 表示i这个数出现了v次
13         for _ in range(v):
14             li.append(i)
15 # 时间复杂度O(n)  看第二层循环n是v的嘛

基数排序

先按照低位进行桶排序,然后按照高位再桶排序,最后挨个出数-->桶排序+关键字排序思想

 1 def radix_sort(li):
 2     max_num = max(li)
 3     i = 0  # 最开始0位(最低位)
 4     while (10 ** i <= max_num):
 5         # do something
 6         # 建立一个桶
 7         buckets = [[] for _ in range(10)]
 8         # 遍历每一个值
 9         for val in li:
10             # 最低位的数字
11             digit = val // (10 ** i) % 10
12             # 把val放在桶里边
13             buckets[digit].append(val)
14         li.clear()
15         # 遍历出来每个桶
16         for bucket in buckets:
17             for val in bucket:
18                 # 把每个桶里边的元素放在li列表中
19                 li.append(val)
20         i += 1

下面是搞着玩的代码

 1 #!/usr/bin/env python
 2 # -*- coding:utf-8 -*-
 3 
 4 
 5 # [1, 2, 3, 4, 5] 0, 1
 6 # [1, 2, 3, 4, 5, 6] 0, 1, 2
 7 # [1, 2, 3, 4, 5, 6, 7]0, 1, 2
 8 # n // 2 -1
 9 
10 
11 def reverse_list(li):
12     n = len(li)
13     for i in range(n // 2):
14         li[i], li[n-i-1] = li[n-i-1], li[i]
15     return li
16 
17 
18 print(reverse_list([1, 2, 3, 4, 5]))
19 
20 
21 def int2list(num):
22     li = []
23     while num > 0:
24         li.append(num % 10)
25         num //= 10
26     li.reverse()
27     return li
28 
29 
30 print(int2list(12345))
31 
32 
33 def reverse_int(num):
34     """
35     123->321 12300->321
36     :param num:
37     :return:
38     """
39     is_neg = False
40     if num < 0:
41         is_neg = True
42         num = -1 * num
43     res = 0
44     while num > 0:
45         res = res * 10
46         digit = num % 10
47         res = res + digit
48         num = num // 10
49     if is_neg:
50         res = res * -1
51     return res
52 
53 
54 print(reverse_int(-100))
55 
56 
57 def get_digit(num, i):
58     """
59 
60     :param num: 57841
61     :param i: i为0 个位1 十位2 百位...  3
62     :return: 7
63     """
64     return num // (10 ** i) % 10

推荐两网站不定期的练算法

　　算法的动画+伪代码https://visualgo.net/en

　　时不时的洗脑壳https://leetcode-cn.com/

posted @ 2019-09-05 21:01 MC_Hotdog 阅读(555) 评论(0) 编辑收藏举报

刷新页面返回顶部