吴恩达机器学习视频笔记——2

4、线性回归

4.4、多变量线性回归(Linear Regression with Multiple Variables) 

参考视频: 4 - 1 - Multiple Features (8 min).mkv 

 假设房价模型有多个特征。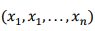

 

 

 

 

 

 4.5、多变量梯度下降

 参考视频: 4 - 2 - Gradient Descent for Multiple Variables (5 min).mkv

 

 

 

 我们开始随机选择一系列的参数值，计算所有的预测结果后，再给所有的参数一个新的值，如此循环直到收敛。

4.6、梯度下降法问题一：特征缩放（归一化）

参考视频: 4 - 3 - Gradient Descent in Practice I - Feature Scaling (9 min).mkv

保证特征都具有相近的尺度，将帮助梯度下降算法更快地收敛，解决的方法是尝试将所有特征的尺度都尽量缩放到-1 到 1 之间。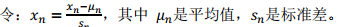

 

 

4.7、梯度下降法问题二：调整学习率

参考视频: 4 - 4 - Gradient Descent in Practice II - Learning Rate (9 min).mkv

梯度下降算法收敛所需要的迭代次数根据模型的不同而不同，我们不能提前预知，我们可以绘制迭代次数和代价函数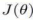的图表来观测算法在何时趋于收敛。 

也有一些自动测试是否收敛的方法，例如将代价函数的变化值与某个阀值（例如 0.001）进行比较，但通常上面这样的图表法效果更好。

梯度下降算法的每次迭代受到学习率的影响，如果学习率𝑎过小，则达到收敛所需的迭代次数会非常高；如果学习率𝑎过大，每次迭代可能不会减小代价函数，可能会越过局部最小值导致无法收敛。

通常可以考虑尝试些学习率：
𝛼 = 0.01， 0.03， 0.1， 0.3， 1， 3， 10

4.8、多项式回归模型和线性回归模型 

 

 

 

 

 

 4.9、正规方程

参考视频: 4 - 6 - Normal Equation (16 min).mkv

 

此处可结合广义逆矩阵知识进行求解。（若A不可逆，通常可检查A中数据单位是否统一及训练集数量是否小于特征数量）

 

 

 

 

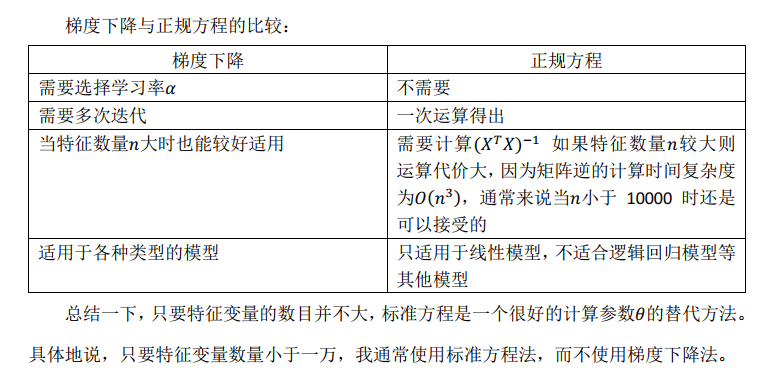
通常，我们会使用一种叫做正则化的线性代数方法，通过删除某些特征或者是使用某些技术，来解决当𝑚比𝑛小的时候的问题。即使你有一个相对较小的训练集，也可使用很多的特征来找到很多合适的
参数。 总之当你发现的矩阵𝑋′𝑋的结果是奇异矩阵，或者找到的其它矩阵是不可逆的，我会建议你这么做。

 

 

 

 

 

 

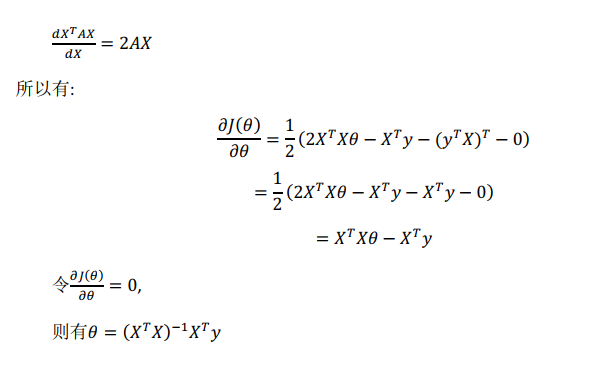
 具体矩阵求导可参考：https://wenku.baidu.com/view/f7fa307a580216fc700afdb9.html

4.10、实例计算

实例计算部分可参见黄海广博士所附代码。

本博客主要引用文章如下：

作者：黄海广
链接：斯坦福大学2014机器学习教程个人笔记（V5.4）
来源：PDF

作者：凌灏文库
链接：https://wenku.baidu.com/view/f7fa307a580216fc700afdb9.html
来源：百度文库

著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。