吴恩达机器学习视频笔记——1
1、机器学习概念
参考视频: 1 - 2 - What is Machine Learning_ (7 min).mkv
1998年来自卡内基梅隆大学的Tom Mitchell对机器学习给出了一个更加正式的定义：A computer program is said to learn from experience E with respect to some task T and some performance measure P,if its performance on T,as measured by P,improves with experience E.
2、监督学习概念
参考视频: 1 - 3 - Supervised Learning (12 min).mkv
监督学习（supervised learning）:监督学习就是给出一组特征，也给出特征所对应的结果。以此来推测另外的特征所对应的结果。（当特征为连续值时属于回归问题，当特征为离散值时为分类问题。）
3、无监督学习概念
参考视频: 1 - 4 - Unsupervised Learning (14 min).mkv
无监督学习（unsupervised learning）:无监督学习就是给出一些特征，但是不给出这些特征所对应的结果，以此来判断这些特征之间有什们结构关系。（聚类问题）
4、线性回归
4.1、单变量线性回归
参考视频: 2 - 1 - Model Representation (8 min).mkv
第一个算法：线性回归（linear regression）
我们将回归问题描述如下：
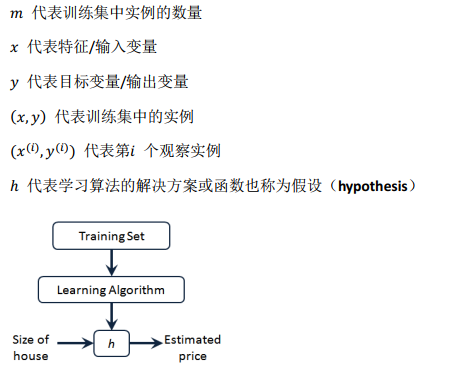
这就是一个监督学习算法的工作方式 。
一种可能的表达方式为：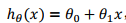
，因为只含有一个特征/输入变量，因此这样的问题叫作单变量线性回归问题。
4.2、代价函数（cost function 成本函数）
参考视频: 2 - 2 - Cost Function (8 min).mkv
为了给模型选择最合适的参数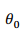
和
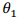，定义建模误差（modeling error）为：模型预测值与训练集中实际值之间的差距 。
我们的目标就是使建模误差的平方和最小，即：
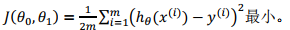其中1/2是为后续数学计算提供便利。
因此单变量线性回归问题可描述为：
代价函数也被称作平方误差函数，有时也被称为平方误差代价函数。我们之所以要求出误差的平方和，是因为误差平方代价函数，对于大多数问题，特别是回归问题，都是一个合理的选择。还有其他的代价函数也能很好地发挥作用，但是平方误差代价函数可能是解决回归问题最常用的手段了。
4.3、梯度下降
梯度下降是一个用来求函数最小值的算法，我们将使用梯度下降算法来求出代价函数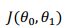
的最小值。
梯度下降背后的思想是：开始时我们随机选择一个参数的组合(𝜃0, 𝜃1, . . . . . . , 𝜃𝑛)，计算代价函数，然后我们寻找下一个能让代价函数值下降最多的参数组合。我们持续这么做直到到到一个局部最小值（ local minimum），因为我们并没有尝试完所有的参数组合，所以不能确定我们得到的局部最小值是否便是全局最小值（ global minimum），选择不同的初始参数组合，可能会找到不同的局部最小值。
其中𝑎是学习率（ learning rate），它决定了我们沿着能让代价函数下降程度最大的方向向下迈出的步子有多大，在批量梯度下降中，我们每一次都同时让所有的参数减去学习速率乘以代价函数的导数。
在这个表达式中，如果你要更新这个等式，你需要同时更新𝜃0和𝜃1。
求出代价函数的导数，即：
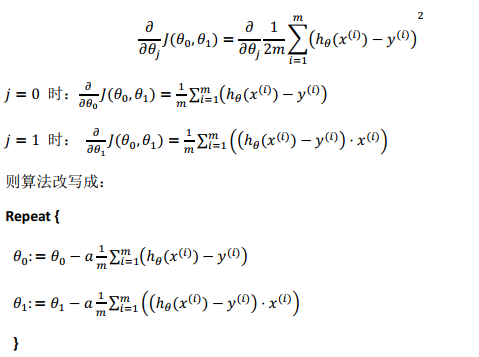
该算法被称为“批量梯度下降”。指的是在梯度下降的每一步中， 我们都用到了所有的训练样本，在梯度下降中，在计算微分求导项时，我们需要进行求和运算，所以，在每一个单独的梯度下降中，我们最终都要计算这样一个东西，这个项需要对所有𝑚个训练样本求和。因此，批量梯度下降法这个名字说明了我们需要考虑所有这一"批"训练样本，而事实上，有时也有其他类型的梯度下降法，不是这种"批量"型的，不考虑整个的训练集，而是每次只关注训练集中的一些小的子集。在后面的课程中，我们也将介绍这些方法。 例如：一种在不需要多步梯度下降的情况下，也能解出代价函数𝐽的最小值，称为正规方程(normal equations)的方法。实际上在数据量较大的情况下，梯度下降法比正规方程要更适用一些。
本博客主要引用文章如下：
作者：黄海广
链接：斯坦福大学2014机器学习教程个人笔记（V5.4）
来源：PDF
作者：辛侠平
链接：https://www.cnblogs.com/xxp17457741/p/8331246.html
来源：博客园
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。
