背包问题

 

第一个问题：01背包问题
时间复杂度O(n*v)，空间复杂度O(v) 其中n是物品个数，v是背包大小。

（x, y） 表示物品大小为x，价值为y
设置状态dpij，表示考虑到前i个物品用大小为j的背包所能装的最大价值
A. 考虑第i个物品可以不要这个物品。dpij = dpi-1j
比如已经用（1, 2）(1, 3)两个物品装进背包，那么此时背包大小为2的时候我们最大价值为5。
现在考虑第三个物品（2，4）来装进背包。当我们枚举到背包大小2的时候，用第三个物品装背包价值会减小，那么这个物品相对前两个“性价比”更低，所以不选。
B. 考虑第i个物品选。dpij = dpi-1j-x + y
比如已经用（1, 2）(1, 3)两个物品装进背包，那么此时背包大小为2的时候我们最大为价值5，背包大小为3的时候最大价值也是5。
现在考虑第三个物品（2，4）来装进背包。当我们枚举到背包大小3的时候，用第三个物品装背包价值会从dp[3 - 1][3 - 2]转移, 发现价值转移完为6。
所以得状态转移方程式：

#include <bits/stdc++.h>
using namespace std;
#define ll long long
#define forn(i, n) for(int i = 0; i < n; ++i)
#define for1(i, n) for(int i = 1; i <= n; ++i)
#define IO ios::sync_with_stdio(false);cin.tie(0)

const int maxn = 1e3 + 5;

int dp[maxn][maxn];

int main() {
    IO;
    int n, V; cin >> n >> V;
    for1(i, n) {
        int c, val; cin >> c >> val;
        for(int j = 1; j <= V; ++j) {
            if(j >= c)
                dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - c] + val);
            else 
                dp[i][j] = dp[i - 1][j];
        }
    } 
    cout << dp[n][V] << '\n';
    return 0;
}

考虑空间优化：
对于一个物品(x,y)，dpij 只会从dpi-1j和dpi-1j-x两个状态转移，对于i-2, i-3的状态都不需要保存，那么代表i-1用完之后就可以抛弃掉。所以第一种优化就是滚动数组。
但是，我们会发现dpij不仅仅只从i-1状态转移，还只从不比j大的状态转移。那么就可以利用枚举顺序来优化。
按照背包大小从大到小的顺序枚举，j从j - x转移的时候，j - x状态还没有被更新，也就是j - x状态保留的就是i-1层的状态。所以就可以优化到一个维度了。

#include <bits/stdc++.h>
using namespace std;
#define ll long long
#define forn(i, n) for(int i = 0; i < n; ++i)
#define for1(i, n) for(int i = 1; i <= n; ++i)
#define IO ios::sync_with_stdio(false);cin.tie(0)

const int maxn = 1e3 + 5;

int dp[maxn];

int main() {
    IO;
    int n, V; cin >> n >> V;
    for1(i, n) {
        int c, val; cin >> c >> val;
        for(int j = V; j >= c; --j) 
            dp[j] = max(dp[j], dp[j - c] + val);
    } 
    cout << dp[V] << '\n';
    return 0;
}

例题1:
背包的两个变种问题：（做法1和做法2）

做法1：求总体积最大，物品体积和价值看作相同的值

做法2：可行性背包，dpj = 1代表恰好把背包j放满

例题2：结合概率

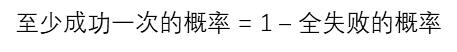
分界线-------------------------------------------------------------------------------------------------------------------------------------------------------

第二个第三个问题：方案数数背包 && 求一种方案的背包
方案数：从谁转移+=谁
输出方案：记录每个状态上一次从谁转移
（其他背包问题的方案数做法也是这么做）


分界线-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------

写不动了，我B站有讲全部的问题。