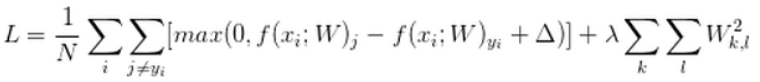深度学习——02、深度学习入门 1-7
01深度学习与人工智能简介
什么是人工智能?
观察周围的世界,把看到的事物加以理解,最后通过理解进行一系列的决策。
感知+理解+决策。
学习的能力,是智能的本质!
大数据时代
大数据时代造就了人工智能的高速发展
深度学习
上世纪九十年代就已经存在。
2012年Alex-net在ImageNet图像分类比赛中一炮打响。
2016年阿尔法狗战胜李世石说明人工智能时代来临。
百度绘制传统AI算法与深度学习算法对比
深度学习述说图片的故事

无人驾驶汽车
1.物体检测
2.行人检测
3.标志识别
4.速度识别
……

02计算机视觉面临挑战与常规套路
图像分类:计算机视觉核心任务
图像在计算机中长什么样呢?

一张图片被表示成三维数组的形式,每个像素的值从0到255。
像素点可以直接与亮度挂钩,像素点越大,亮度越高。
挑战:照射角度
挑战:光照强度
挑战:形状改变
挑战:部分遮蔽
挑战:背景混入
深度学习的套路
1.收集数据并给定标签
2.训练一个分类器
3.测试,评估
03用K近邻来进行图像分类
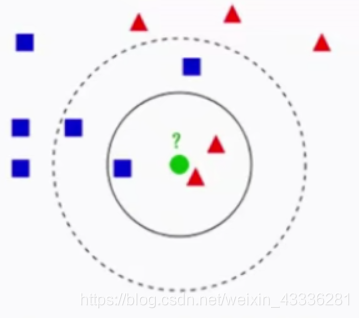
1.如果K=3,绿色圆点的最近3个邻居是2个红色小三角形和1个蓝色小正方形,少数服从多数,基于统计的方法,判定绿色的这个待分类点属于红色的三角形一类。
2. 如果K=5,绿色圆点的最近5个邻居是2个红色小三角形和3个蓝色小正方形,少数服从多数,基于统计的方法,判定绿色的这个待分类点属于蓝色的正方形一类。
对于未知类别属性数据集中的点:
1.计算已知类别数据集中的点与当前点的距离
2.按照距离依次排序
3.选取与当前距离最小的K个点
(K最好选为奇数)
4.确定前K个点所在类别的出现概率
5.返回前K个点出现概率最高的类别作为当前点的预测分类
K-近邻概述
KNN算法本身简单有效,它是一种lazy-learning算法。
分类器不需要使用训练集进行训练,训练时间复杂度为0。
KNN分类的计算复杂度和训练集中的文档数目成正比,也就是说,如果训练集中文档总数为n,那么KNN的分类时间复杂度为O(n)。
K-近邻缺陷
K值的选择,距离度量和分类决策规划是该算法的三个基本要素。
问题:该算法在分类时有个主要的不足是,当样本不平衡时,如一个类的样本容量很大,而其他类样本容量很小时,有可能导致当输入一个新样本时,该样本的K个邻居大容量类的样本占多数。
解决,不同的样本给予不同权重项。
数据库样例:CIFAR-10
10类标签
50000个训练数据
10000个测试数据
大小均为32*32
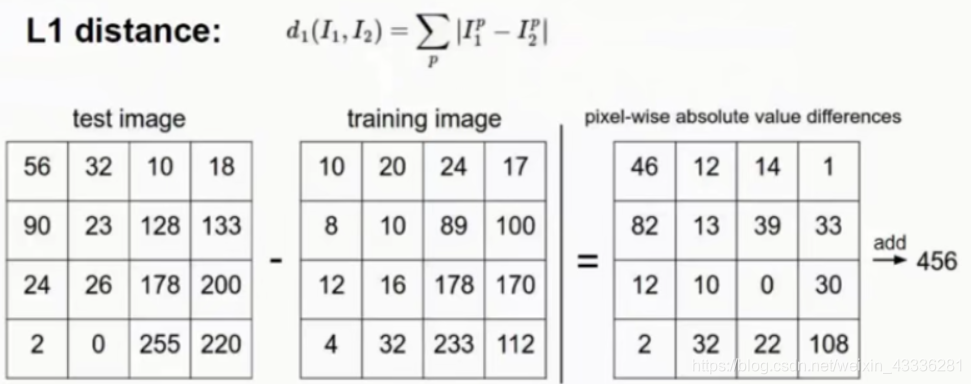
如何计算
04超参数与交叉验证
超参数

问题:
1.对于距离如何设定?
2.对于K近邻的K该如何选择?
3.如果有的话,其他超参数该怎么设定?
解决:
找到最好的参数:多次用测试数据实验,找到做好的一组参数组合。
但这是错误的想法,因为测试数据只能最终使用。
交叉验证
背景主导导致不能用K-近邻进行图片分类
总结
1.选取超参数的正确方法是:将原始训练集分为训练集和验证集,我们在验证集上尝试不同的超参数,最后保留表现最好那个。
2.如果训练数据量不够,使用交叉验证方法,它能帮助我们在选取最优超参数的时候减少噪音。
3.一旦找到最优的超参数,就让算法以该参数在测试集跑且只跑一次,并根据测试结果评价算法。
4.最近邻分类器能够在CIFAR-10上得到将近40%的准确率。该算法简单易实现,但需要存储所有训练数据,并且在测试的时候过于耗费计算能力。
5.最后,仅仅使用L1和L2范数来进行像素比较是不够的,图像更多的是按照背景和颜色被分类,而不是语义主体分身。
6.预处理你的数据:对你数据中的特征进行归一化(normalize),让其具有零平均值(zero mean)和单位方差(unit variance)。
7.如果数据是高维数据,考虑使用降维方法,比如PCA。
8.将数据随机分入训练集和验证集。按照一般规律,70%-90% 数据作为训练集。
9.在验证集上调优,尝试足够多的k值,尝试L1和L2两种范数计算方式。
05线性分类

假设有这么一张我学校的校徽图片,对应大小为[32323],然后有十个标签, 想要找一组比较好的权重参数w,得出当前的权重参数对每个分类的得分。

转换为矩阵形式:
将32323=3072个像素点进行拉伸,转换成一个列向量:30721的矩阵,结果是101的矩阵, 则w为3072*10的二维矩阵,每个元素都是一个权重参数,跟图像转换的矩阵进行组合,就可以算出得分。
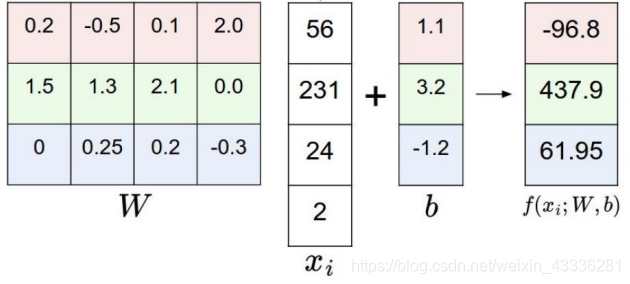
06损失函数
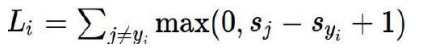

07正则化惩罚项
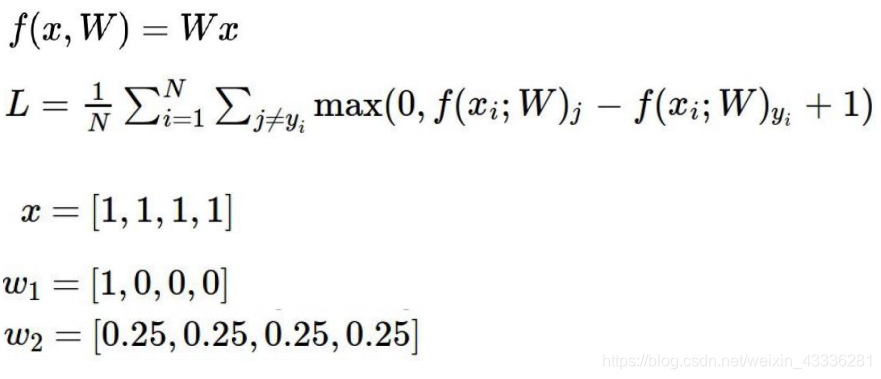
w1只关注第一个像素点,w2对每个像素点一视同仁,虽然结果相同,但是对于w1是不可取的。
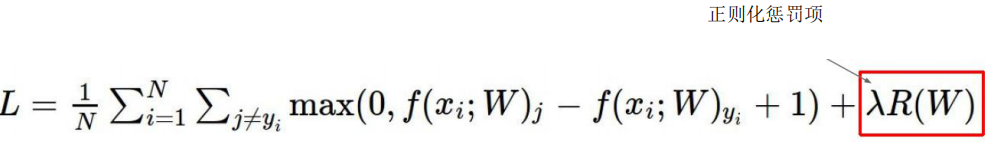
由此可得,损失函数终极版: