第六章 定积分的应用 —— 第一节 定积分的元素法

定积分的元素法是在应用定积分的理论来分析和解决一些几何，物理中的问题时，需要将一个量表达成为定积分的分析方法。

步骤
一般的，如果某一实际问题中的所求量U符合下列条件：
（1）U是与一个变量x的变化区间[a,b]有关的量；
（2）U对于区间[a,b]具有可加性，就是说，如果把区间[a,b]分成许多小区间，则U相应的分成许多部分量，而U等于所有部分量之和；
（3）部分量ΔU_i近似值可表示为f(ξ_i)Δx_i，那么就可以考虑用定积分来表达这个量U。

通常写出这个量U的积分表达式的步骤是：
1）根据问题的具体情况，选取一个变量例如x为积分变量，并确定他的变化区间[a,b]；
2）设想把区间[a,b]分成n个小区间，选取其中任一个小区间并记作[x,x+dx]，求出相应于这个小区间的部分量△U的近似值。如果△U能近似的表示为[a,b]上的一个连续函数在x处的值f(x)于定积分dx的乘积，就把f(x)dx称为量U的元素且记作dU，即

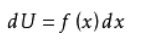
3）以所求量U的元素f(x)dx为被积表达式，在区间[a,b]上作定积分，得

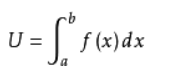
这就是所求量U的积分表达式。
上面所用的方法就是元素法。