Tree Walk Aizu - ALDS1_7_C
Binary trees are defined recursively. A binary tree T is a structure defined on a finite set of nodes that either
contains no nodes, or
is composed of three disjoint sets of nodes:
- a root node.
- a binary tree called its left subtree.
- a binary tree called its right subtree.
Your task is to write a program which perform tree walks (systematically traverse all nodes in a tree) based on the following algorithms:
Print the root, the left subtree and right subtree (preorder).
Print the left subtree, the root and right subtree (inorder).
Print the left subtree, right subtree and the root (postorder).
Here, the given binary tree consists of n nodes and evey node has a unique ID from 0 to n-1.
Input
The first line of the input includes an integer n, the number of nodes of the tree.
In the next n linen, the information of each node is given in the following format:
id left right
id is the node ID, left is ID of the left child and right is ID of the right child. If the node does not have the left (right) child, the left(right) is indicated by -1
Output
In the 1st line, print “Preorder”, and in the 2nd line print a list of node IDs obtained by the preorder tree walk.
In the 3rd line, print “Inorder”, and in the 4th line print a list of node IDs obtained by the inorder tree walk.
In the 5th line, print “Postorder”, and in the 6th line print a list of node IDs obtained by the postorder tree walk.
Print a space character before each node ID.
Constraints
1 ≤ n ≤ 25
Sample Input 1
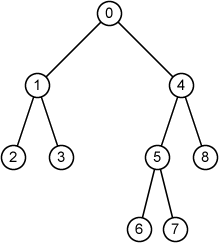
9
0 1 4
1 2 3
2 -1 -1
3 -1 -1
4 5 8
5 6 7
6 -1 -1
7 -1 -1
8 -1 -1
Sample Output 1
Preorder
0 1 2 3 4 5 6 7 8
Inorder
2 1 3 0 6 5 7 4 8
Postorder
2 3 1 6 7 5 8 4 0
Reference
Introduction to Algorithms, Thomas H. Cormen, Charles E. Leiserson, Ronald L. Rivest, and Clifford Stein. The MIT Press.
Code
/*
^....0
^ .1 ^1^
.. 01
1.^ 1.0
^ 1 ^ ^0.1
1 ^ ^..^
0. ^ 0^
.0 1 .^
.1 ^0 .........001^
.1 1. .111100....01^
00 11^ ^1. .1^
1.^ ^0 0^
.^ ^0..1
.1 1..^
1 .0 ^ ^
00. ^^0.^
^ 0 ^^110.^
0 0 ^ ^^^10.01
^^ 10 1 1 ^^^1110.1
01 10 1.1 ^^^1111110
010 01 ^^ ^^^1111^1.^ ^^^
10 10^ 0^ 1 ^^111^^^0.1^ 1....^
11 0 ^^11^^^ 0.. ....1^ ^ ^
1. 0^ ^11^^^ ^ 1 111^ ^ 0.
10 00 11 ^^^^^ 1 0 1.
0^ ^0 ^0 ^^^^ 0 0.
0^ 1.0 .^ ^^^^ 1 1 .0
^.^ ^^ 0^ ^1 ^^^^ 0. ^.1
1 ^ 11 1. ^^^ ^ ^ ..^
^..^ ^1 ^.^ ^^^ .0 ^.0
0..^ ^0 01 ^^^ .. 0..^
1 .. .1 ^.^ ^^^ 1 ^ ^0001
^ 1. 00 0. ^^^ ^.0 ^.1
. 0^. ^.^ ^.^ ^^^ ..0.0
1 .^^. .^ 1001 ^^ ^^^ . 1^
. ^ ^. 11 0. 1 ^ ^^ 0.
0 ^. 0 ^0 1 ^^^ 0.
0.^ 1. 0^ 0 .1 ^^^ ..
.1 1. 00 . .1 ^^^ ..
1 1. ^. 0 .^ ^^ ..
0. 1. .^ . 0 .
.1 1. 01 . . ^ 0
^.^ 00 ^0 1. ^ 1 1
.0 00 . ^^^^^^ .
.^ 00 01 ..
1. 00 10 1 ^
^.1 00 ^. ^^^ .1
.. 00 .1 1..01 ..
1.1 00 1. ..^ 10
^ 1^ 00 ^.1 0 1 1
.1 00 00 ^ 1 ^
. 00 ^.^ 10^ ^^
1.1 00 00 10^
..^ 1. ^. 1.
0 1 ^. 00 00 .^
^ ^. ^ 1 00 ^0000^ ^ 01
1 0 ^. 00.0^ ^00000 1.00.1 11
. 1 0 1^^0.01 ^^^ 01
.^ ^ 1 1^^ ^.^
1 1 0.
.. 1 ^
1 1
^ ^ .0
1 ^ 1
.. 1.1 ^0.0
^ 0 1..01^^100000..0^
1 1 ^ 1 ^^1111^ ^^
0 ^ ^ 1 1000^
.1 ^.^ . 00
.. 1.1 0. 0
1. . 1. .^
1. 1 1. ^0
^ . ^.1 00 01
^.0 001. .^
*/
// Virtual_Judge —— Tree Walk Aizu - ALDS1_7_C.cpp created by VB_KoKing on 2019-05-08:20.
/* Procedural objectives:
Variables required by the program:
Procedural thinking:
Functions required by the program:
Determination algorithm:
Determining data structure:
*/
/* My dear Max said:
"I like you,
So the first bunch of sunshine I saw in the morning is you,
The first gentle breeze that passed through my ear is you,
The first star I see is also you.
The world I see is all your shadow."
FIGHTING FOR OUR FUTURE!!!
*/
#include <iostream>
#define MAX 10007
#define NIL -1
using namespace std;
struct Node {int parent, left, right;};
struct Node T[MAX];
int n;
//前序遍历
void pre_parse(int u) {
if (u == NIL) return;
cout << " " << u;
pre_parse(T[u].left);
pre_parse(T[u].right);
}
//中序遍历
void in_parse(int u) {
if (u == NIL) return;
in_parse(T[u].left);
cout << " " << u;
in_parse(T[u].right);
}
//后序遍历
void post_parse(int u) {
if (u == NIL) return;
post_parse(T[u].left);
post_parse(T[u].right);
cout << " " << u;
}
int main() {
cin>>n;
int v, l, r, root;
for (int i = 0; i < n; i++)
T[i].parent = NIL;
for (int i = 0; i < n; i++) {
cin >> v >> l >> r;
T[v].left = l;
T[v].right = r;
if (l != NIL) T[l].parent = v;
if (r != NIL) T[r].parent = v;
}
for (int i = 0; i < n; i++)
if (T[i].parent == NIL)
root = i;
cout << "Preorder" << endl;
pre_parse(root);
cout << endl << "Inorder" << endl;
in_parse(root);
cout << endl << "Postorder" << endl;
post_parse(root);
cout << endl;
return 0;
}



