Complete Binary Tree Aizu - ALDS1_9_A
A complete binary tree is a binary tree in which every internal node has two children and all leaves have the same depth. A binary tree in which if last level is not completely filled but all nodes (leaves) are pushed across to the left, is also (nearly) a complete binary tree.
A binary heap data structure is an array that can be viewed as a nearly complete binary tree as shown in the following figure.
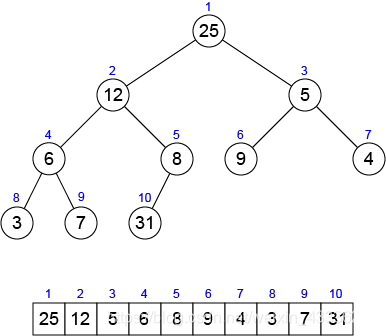
Each node of a nearly complete binary tree corresponds to an element of the array that stores the value in the node. An array A that represents a binary heap has the heap size H, the number of elements in the heap, and each element of the binary heap is stored into A[1…H] respectively. The root of the tree is A[1], and given the index i of a node, the indices of its parent parent(i), left child left(i), right child right(i) can be computed simply by ⌊i/2⌋, 2×i and 2×i+1 respectively.
Write a program which reads a binary heap represented by a nearly complete binary tree, and prints properties of nodes of the binary heap in the following format:
node id: key = k, parent key = pk, left key = lk, right key = rk,
id, k, pk, lk and rk represent id (index) of the node, value of the node, value of its parent, value of its left child and value of its right child respectively. Print these properties in this order. If there are no appropriate nodes, print nothing.
Input
In the first line, an integer H, the size of the binary heap, is given. In the second line, H integers which correspond to values assigned to nodes of the binary heap are given in order of node id (from 1 to H).
Output
Print the properties of the binary heap in the above format from node 1 to H in order. Note that, the last character of each line is a single space character.
Constraints
H≤250
−2,000,000,000≤ value of a node ≤2,000,000,000
Sample Input 1
5
7 8 1 2 3
Sample Output 1
node 1: key = 7, left key = 8, right key = 1,
node 2: key = 8, parent key = 7, left key = 2, right key = 3,
node 3: key = 1, parent key = 7,
node 4: key = 2, parent key = 8,
node 5: key = 3, parent key = 8,
Reference
Introduction to Algorithms, Thomas H. Cormen, Charles E. Leiserson, Ronald L. Rivest, and Clifford Stein. The MIT Press.
Code
/*
^....0
^ .1 ^1^
.. 01
1.^ 1.0
^ 1 ^ ^0.1
1 ^ ^..^
0. ^ 0^
.0 1 .^
.1 ^0 .........001^
.1 1. .111100....01^
00 11^ ^1. .1^
1.^ ^0 0^
.^ ^0..1
.1 1..^
1 .0 ^ ^
00. ^^0.^
^ 0 ^^110.^
0 0 ^ ^^^10.01
^^ 10 1 1 ^^^1110.1
01 10 1.1 ^^^1111110
010 01 ^^ ^^^1111^1.^ ^^^
10 10^ 0^ 1 ^^111^^^0.1^ 1....^
11 0 ^^11^^^ 0.. ....1^ ^ ^
1. 0^ ^11^^^ ^ 1 111^ ^ 0.
10 00 11 ^^^^^ 1 0 1.
0^ ^0 ^0 ^^^^ 0 0.
0^ 1.0 .^ ^^^^ 1 1 .0
^.^ ^^ 0^ ^1 ^^^^ 0. ^.1
1 ^ 11 1. ^^^ ^ ^ ..^
^..^ ^1 ^.^ ^^^ .0 ^.0
0..^ ^0 01 ^^^ .. 0..^
1 .. .1 ^.^ ^^^ 1 ^ ^0001
^ 1. 00 0. ^^^ ^.0 ^.1
. 0^. ^.^ ^.^ ^^^ ..0.0
1 .^^. .^ 1001 ^^ ^^^ . 1^
. ^ ^. 11 0. 1 ^ ^^ 0.
0 ^. 0 ^0 1 ^^^ 0.
0.^ 1. 0^ 0 .1 ^^^ ..
.1 1. 00 . .1 ^^^ ..
1 1. ^. 0 .^ ^^ ..
0. 1. .^ . 0 .
.1 1. 01 . . ^ 0
^.^ 00 ^0 1. ^ 1 1
.0 00 . ^^^^^^ .
.^ 00 01 ..
1. 00 10 1 ^
^.1 00 ^. ^^^ .1
.. 00 .1 1..01 ..
1.1 00 1. ..^ 10
^ 1^ 00 ^.1 0 1 1
.1 00 00 ^ 1 ^
. 00 ^.^ 10^ ^^
1.1 00 00 10^
..^ 1. ^. 1.
0 1 ^. 00 00 .^
^ ^. ^ 1 00 ^0000^ ^ 01
1 0 ^. 00.0^ ^00000 1.00.1 11
. 1 0 1^^0.01 ^^^ 01
.^ ^ 1 1^^ ^.^
1 1 0.
.. 1 ^
1 1
^ ^ .0
1 ^ 1
.. 1.1 ^0.0
^ 0 1..01^^100000..0^
1 1 ^ 1 ^^1111^ ^^
0 ^ ^ 1 1000^
.1 ^.^ . 00
.. 1.1 0. 0
1. . 1. .^
1. 1 1. ^0
^ . ^.1 00 01
^.0 001. .^
*/
// Virtual_Judge —— Complete Binary Tree Aizu - ALDS1_9_A .cpp created by VB_KoKing on 2019-05-10:09.
/* Procedural objectives:
Variables required by the program:
Procedural thinking:
Functions required by the program:
Determination algorithm:
Determining data structure:
*/
/* My dear Max said:
"I like you,
So the first bunch of sunshine I saw in the morning is you,
The first gentle breeze that passed through my ear is you,
The first star I see is also you.
The world I see is all your shadow."
FIGHTING FOR OUR FUTURE!!!
*/
#include <iostream>
#define MAX 100007
using namespace std;
int parent(int i) { return i/2;}
int left(int i) { return 2*i;}
int right(int i) { return 2*i+1;}
int main()
{
int H,A[MAX];
cin>>H;
for (int i = 1; i < H+1; i++)
cin>>A[i];
for (int i = 1; i < H+1; i++) {
cout<<"node "<<i<<": key = "<<A[i]<<", ";
if (parent(i)>0) cout<<"parent key = "<<A[parent(i)]<<", ";
if (left(i)<H+1) cout<<"left key = "<<A[left(i)]<<", ";
if (right(i)<H+1) cout<<"right key = "<<A[right(i)]<<", ";
cout<<endl;
}
return 0;
}



 浙公网安备 33010602011771号
浙公网安备 33010602011771号