Maximum Heap Aizu - ALDS1_9_B
A binary heap which satisfies max-heap property is called max-heap. In a max-heap, for every node i other than the root, A[i]≤A[parent(i)], that is, the value of a node is at most the value of its parent. The largest element in a max-heap is stored at the root, and the subtree rooted at a node contains values no larger than that contained at the node itself.
Here is an example of a max-heap.
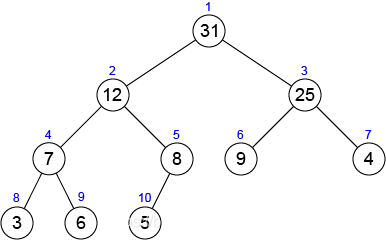
Write a program which reads an array and constructs a max-heap from the array based on the following pseudo code.
maxHeapify(A,i) move the value of A[i] down to leaves to make a sub-tree of node i a max-heap. Here, H is the size of the heap.
1 maxHeapify(A, i)
2 l = left(i)
3 r = right(i)
4 // select the node which has the maximum value
5 if l ≤ H and A[l] > A[i]
6 largest = l
7 else
8 largest = i
9 if r ≤ H and A[r] > A[largest]
10 largest = r
11
12 if largest ≠ i // value of children is larger than that of i
13 swap A[i] and A[largest]
14 maxHeapify(A, largest) // call recursively
The following procedure buildMaxHeap(A) makes A a max-heap by performing maxHeapify in a bottom-up manner.
1 buildMaxHeap(A)
2 for i = H/2 downto 1
3 maxHeapify(A, i)
Input
In the first line, an integer H is given. In the second line, H integers which represent elements in the binary heap are given in order of node id (from 1 to H).
Output
Print values of nodes in the max-heap in order of their id (from 1 to H). Print a single space character before each value.
Constraint
1≤H≤500,000
−2,000,000,000≤ value of a node ≤2,000,000,000
Sample Input 1
10
4 1 3 2 16 9 10 14 8 7
Sample Output 1
16 14 10 8 7 9 3 2 4 1
Reference
Introduction to Algorithms, Thomas H. Cormen, Charles E. Leiserson, Ronald L. Rivest, and Clifford Stein. The MIT Press.
Code
/*
^....0
^ .1 ^1^
.. 01
1.^ 1.0
^ 1 ^ ^0.1
1 ^ ^..^
0. ^ 0^
.0 1 .^
.1 ^0 .........001^
.1 1. .111100....01^
00 11^ ^1. .1^
1.^ ^0 0^
.^ ^0..1
.1 1..^
1 .0 ^ ^
00. ^^0.^
^ 0 ^^110.^
0 0 ^ ^^^10.01
^^ 10 1 1 ^^^1110.1
01 10 1.1 ^^^1111110
010 01 ^^ ^^^1111^1.^ ^^^
10 10^ 0^ 1 ^^111^^^0.1^ 1....^
11 0 ^^11^^^ 0.. ....1^ ^ ^
1. 0^ ^11^^^ ^ 1 111^ ^ 0.
10 00 11 ^^^^^ 1 0 1.
0^ ^0 ^0 ^^^^ 0 0.
0^ 1.0 .^ ^^^^ 1 1 .0
^.^ ^^ 0^ ^1 ^^^^ 0. ^.1
1 ^ 11 1. ^^^ ^ ^ ..^
^..^ ^1 ^.^ ^^^ .0 ^.0
0..^ ^0 01 ^^^ .. 0..^
1 .. .1 ^.^ ^^^ 1 ^ ^0001
^ 1. 00 0. ^^^ ^.0 ^.1
. 0^. ^.^ ^.^ ^^^ ..0.0
1 .^^. .^ 1001 ^^ ^^^ . 1^
. ^ ^. 11 0. 1 ^ ^^ 0.
0 ^. 0 ^0 1 ^^^ 0.
0.^ 1. 0^ 0 .1 ^^^ ..
.1 1. 00 . .1 ^^^ ..
1 1. ^. 0 .^ ^^ ..
0. 1. .^ . 0 .
.1 1. 01 . . ^ 0
^.^ 00 ^0 1. ^ 1 1
.0 00 . ^^^^^^ .
.^ 00 01 ..
1. 00 10 1 ^
^.1 00 ^. ^^^ .1
.. 00 .1 1..01 ..
1.1 00 1. ..^ 10
^ 1^ 00 ^.1 0 1 1
.1 00 00 ^ 1 ^
. 00 ^.^ 10^ ^^
1.1 00 00 10^
..^ 1. ^. 1.
0 1 ^. 00 00 .^
^ ^. ^ 1 00 ^0000^ ^ 01
1 0 ^. 00.0^ ^00000 1.00.1 11
. 1 0 1^^0.01 ^^^ 01
.^ ^ 1 1^^ ^.^
1 1 0.
.. 1 ^
1 1
^ ^ .0
1 ^ 1
.. 1.1 ^0.0
^ 0 1..01^^100000..0^
1 1 ^ 1 ^^1111^ ^^
0 ^ ^ 1 1000^
.1 ^.^ . 00
.. 1.1 0. 0
1. . 1. .^
1. 1 1. ^0
^ . ^.1 00 01
^.0 001. .^
*/
// Virtual_Judge —— Maximum Heap Aizu - ALDS1_9_B .cpp created by VB_KoKing on 2019-05-10:09.
/* Procedural objectives:
Variables required by the program:
Procedural thinking:
Functions required by the program:
Determination algorithm:
Determining data structure:
*/
/* My dear Max said:
"I like you,
So the first bunch of sunshine I saw in the morning is you,
The first gentle breeze that passed through my ear is you,
The first star I see is also you.
The world I see is all your shadow."
FIGHTING FOR OUR FUTURE!!!
*/
#include <iostream>
#define MAX 2000007
using namespace std;
int H, A[MAX];
void max_heapify(int i) {
int l, r, largest;
l = 2 * i;
r = 2 * i + 1;
if (l < H + 1 && A[l] > A[i]) largest = l;
else largest = i;
if (r < H + 1 && A[r] > A[largest]) largest = r;
if (largest != i){
swap(A[i],A[largest]);
max_heapify(largest);
}
}
int main(){
cin>>H;
for (int i = 1; i < H+1; i++) cin>>A[i];
for (int i = H/2; i > 0; i--) max_heapify(i);
for (int i = 1; i < H+1; i++) cout<<' '<<A[i];
cout<<endl;
return 0;
}



