2017年第八届蓝桥杯C/C++ B组国赛 —— 第三题:希尔伯特曲线
标题:希尔伯特曲线
希尔伯特曲线是以下一系列分形曲线 Hn 的极限。我们可以把 Hn 看作一条覆盖 2n × 2n 方格矩阵的曲线,曲线上一共有 2n × 2n 个顶点(包括左下角起点和右下角终点),恰好覆盖每个方格一次。
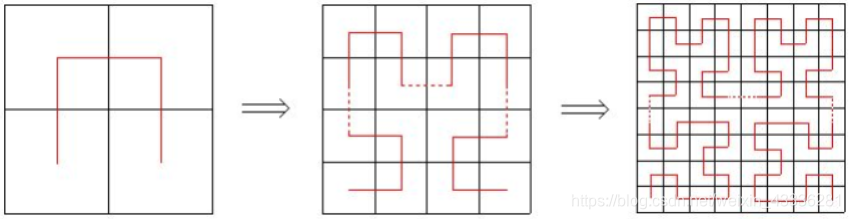
Hn(n > 1)可以通过如下方法构造:
- 将 Hn-1 顺时针旋转90度放在左下角
- 将 Hn-1 逆时针旋转90度放在右下角
- 将2个 Hn-1 分别放在左上角和右上角
- 用3条单位线段把4部分连接起来
对于 Hn 上每一个顶点 p ,我们定义 p 的坐标是它覆盖的小方格在矩阵中的坐标(左下角是(1, 1),右上角是(2n, 2n),从左到右是X轴正方向,从下到上是Y轴正方向),
定义 p 的序号是它在曲线上从起点开始数第几个顶点(从1开始计数)。
以下程序对于给定的n(n <= 30)和p点坐标(x, y),输出p点的序号。请仔细阅读分析源码,填写划线部分缺失的内容。
#include <stdio.h>
long long f(int n, int x, int y) {
if (n == 0) return 1;
int m = 1 << (n - 1);
if (x <= m && y <= m) {
return f(n - 1, y, x);
}
if (x > m && y <= m) {
return 3LL * m * m + f(n - 1, ________________ , m * 2 - x + 1); // 填空
}
if (x <= m && y > m) {
return 1LL * m * m + f(n - 1, x, y - m);
}
if (x > m && y > m) {
return 2LL * m * m + f(n - 1, x - m, y - m);
}
}
int main() {
int n, x, y;
scanf("%d %d %d", &n, &x, &y);
printf("%lld", f(n, x, y));
return 0;
}
注意:只填写划线处缺少的内容,不要填写已有的代码或符号,也不要填写任何解释说明文字等。
Code
/*
^....0
^ .1 ^1^
.. 01
1.^ 1.0
^ 1 ^ ^0.1
1 ^ ^..^
0. ^ 0^
.0 1 .^
.1 ^0 .........001^
.1 1. .111100....01^
00 11^ ^1. .1^
1.^ ^0 0^
.^ ^0..1
.1 1..^
1 .0 ^ ^
00. ^^0.^
^ 0 ^^110.^
0 0 ^ ^^^10.01
^^ 10 1 1 ^^^1110.1
01 10 1.1 ^^^1111110
010 01 ^^ ^^^1111^1.^ ^^^
10 10^ 0^ 1 ^^111^^^0.1^ 1....^
11 0 ^^11^^^ 0.. ....1^ ^ ^
1. 0^ ^11^^^ ^ 1 111^ ^ 0.
10 00 11 ^^^^^ 1 0 1.
0^ ^0 ^0 ^^^^ 0 0.
0^ 1.0 .^ ^^^^ 1 1 .0
^.^ ^^ 0^ ^1 ^^^^ 0. ^.1
1 ^ 11 1. ^^^ ^ ^ ..^
^..^ ^1 ^.^ ^^^ .0 ^.0
0..^ ^0 01 ^^^ .. 0..^
1 .. .1 ^.^ ^^^ 1 ^ ^0001
^ 1. 00 0. ^^^ ^.0 ^.1
. 0^. ^.^ ^.^ ^^^ ..0.0
1 .^^. .^ 1001 ^^ ^^^ . 1^
. ^ ^. 11 0. 1 ^ ^^ 0.
0 ^. 0 ^0 1 ^^^ 0.
0.^ 1. 0^ 0 .1 ^^^ ..
.1 1. 00 . .1 ^^^ ..
1 1. ^. 0 .^ ^^ ..
0. 1. .^ . 0 .
.1 1. 01 . . ^ 0
^.^ 00 ^0 1. ^ 1 1
.0 00 . ^^^^^^ .
.^ 00 01 ..
1. 00 10 1 ^
^.1 00 ^. ^^^ .1
.. 00 .1 1..01 ..
1.1 00 1. ..^ 10
^ 1^ 00 ^.1 0 1 1
.1 00 00 ^ 1 ^
. 00 ^.^ 10^ ^^
1.1 00 00 10^
..^ 1. ^. 1.
0 1 ^. 00 00 .^
^ ^. ^ 1 00 ^0000^ ^ 01
1 0 ^. 00.0^ ^00000 1.00.1 11
. 1 0 1^^0.01 ^^^ 01
.^ ^ 1 1^^ ^.^
1 1 0.
.. 1 ^
1 1
^ ^ .0
1 ^ 1
.. 1.1 ^0.0
^ 0 1..01^^100000..0^
1 1 ^ 1 ^^1111^ ^^
0 ^ ^ 1 1000^
.1 ^.^ . 00
.. 1.1 0. 0
1. . 1. .^
1. 1 1. ^0
^ . ^.1 00 01
^.0 001. .^
*/
// VB_king —— 2017_Finals_B_C++_3.cpp created by VB_KoKing on 2019-05-14:07.
/* Procedural objectives:
Variables required by the program:
Procedural thinking:
每个网格中的1*1的方格都对应曲线上的一个顶点——即使有些1*1的方格内不存在转折点,但也是曲线上的一个顶点。
Functions required by the program:
Determination algorithm:
Determining data structure:
*/
/* My dear Max said:
"I like you,
So the first bunch of sunshine I saw in the morning is you,
The first gentle breeze that passed through my ear is you,
The first star I see is also you.
The world I see is all your shadow."
FIGHTING FOR OUR FUTURE!!!
*/
#include <stdio.h>
long long f(int n, int x, int y) {
if (n == 0) return 1;
int m = 1 << (n - 1); // m存储的就是边长为:pow(2,n)的正方形的二分之一的长
/*
四个 return 返回给上一层都是当前层顶点(x,y)的序号
根据曲线的走势,左下角是序号的第一部分,其次是左上角、右上角、右下角
要求左上角的顶点序号,应该要加上左下角的顶点数:1LL*m*m;
要求右下角的顶点序号,要加上前面三部分(左下角、左上角、右上角)的顶点数:3LL * m * m
f()代表的是下一层传过来的点序号
所以 '+' 左边的部分加上右边的部分==(x,y)的序号
*/
if (x <= m && y <= m) { //左下角
return f(n - 1, y, x);
}
if (x > m && y <= m) { //右下角
return 3LL * m * m + f(n - 1, m + 1 - y, m * 2 - x + 1);
/*
下一层的 y 和当前层的 x 是相关联的,
所以推测下一层的 x 和当前层的 y 是相关联的;
设当前层的坐标为 (x',y'),下一层的坐标为(x,y);
所以 y = 2 * m - x' + 1;即 x' = 2 * m - y + 1;(用下一层的坐标表示当前层的坐标)
可设 y’ = m*a + b*x + c;由于 m已知,所以可化简为 y' = b*x + F
从B、C两图中找出可以带入上式求出未知参数的坐标;
(1,1)——> (8,4)
(2,1)——> (8,3)
(3,1)——> (8,2)
左边的坐标从B图中任意取,右边的坐标要从C图的右下角部分取;
比如B图中的序号为7的顶点的坐标为(2,4);在C图右下角也找到序号为7的顶点,坐标为(5,3);
将左边坐标的横坐标、右边坐标的纵坐标代入 y' = b*x + F 得:
4=b+F;
3=2b+F;
解得 b = -1,F=5;
所以 m*a+c=5;从 x' 的表达式很容易就可以推测出 F = m + 1;
*/
}
if (x <= m && y > m) { //左上角
return 1LL * m * m + f(n - 1, x, y - m);
}
if (x > m && y > m) { //右上角
return 2LL * m * m + f(n - 1, x - m, y - m);
}
}
int main() {
int n, x, y;
scanf("%d %d %d", &n, &x, &y);
printf("%lld", f(n, x, y));
return 0;
}



