那就别担心了 - 题解【记忆化搜索】
题面
这是2020年天梯赛的L3-1题。
下图转自“英式没品笑话百科”的新浪微博 —— 所以无论有没有遇到难题,其实都不用担心。
博主将这种逻辑推演称为“逻辑自洽”,即从某个命题出发的所有推理路径都会将结论引导到同一个最终命题(开玩笑的,千万别以为这是真正的逻辑自洽的定义……)。现给定一个更为复杂的逻辑推理图,本题就请你检查从一个给定命题到另一个命题的推理是否是“逻辑自洽”的,以及存在多少种不同的推理路径。例如上图,从“你遇到难题了吗?”到“那就别担心了”就是一种“逻辑自洽”的推理,一共有 3 条不同的推理路径。
输入格式:
输入首先在一行中给出两个正整数$ N (1<N≤500)$和 \(M\),分别为命题个数和推理个数。这里我们假设命题从 1 到 \(N\) 编号。接下来 \(M\) 行,每行给出一对命题之间的推理关系,即两个命题的编号 \(S_1, S_2\),表示可以从 \(S_1\) 推出 \(S_2\)。题目保证任意两命题之间只存在最多一种推理关系,且任一命题不能循环自证(即从该命题出发推出该命题自己)。
最后一行给出待检验的两个命题的编号 \(A \enspace B\)。
输出格式:
在一行中首先输出从 A 到 B 有多少种不同的推理路径,然后输出Yes如果推理是“逻辑自洽”的,或No如果不是。题目保证输出数据不超过 \(10^9\) 。
输入样例 1:
7 8 7 6 7 4 6 5 4 1 5 2 5 3 2 1 3 1 7 1输出样例 1:
3 Yes输入样例 2:
7 8 7 6 7 4 6 5 4 1 5 2 5 3 6 1 3 1 7 1输出样例 2:
3 No
题解
这道题啰里八嗦讲了这么多的背景故事,实际上题意就是:给定一个有向无环图(DAG),并且给出起点A和终点B,问从A出发的所有路径是否都能到达B,并且求出从A出发到达B的不同路径有多少条。第一个问题非常好解,只要从A开始DFS,如果搜到某个出度为0的点,并且这个点不是题面给出的B点,就说明并不是所有从A出发的路径都能到达B。对于第二个问题,虽然这道题数据比较小,最多只有500个点,但是这题的时间限制是400ms,对于求解不同路径的问题,如果暴力搜索的话是一定会超时的(题面保证输出数据不超过$ 10^9 $)。实际上,这道题30分,暴力加上各种玄学优化可以骗到25分。不过如果拿满,我们需要一点优化策略。
我们从DFS的过程进行考虑,假设有这样的一个DAG,要求起点1到终点7的所有路径。
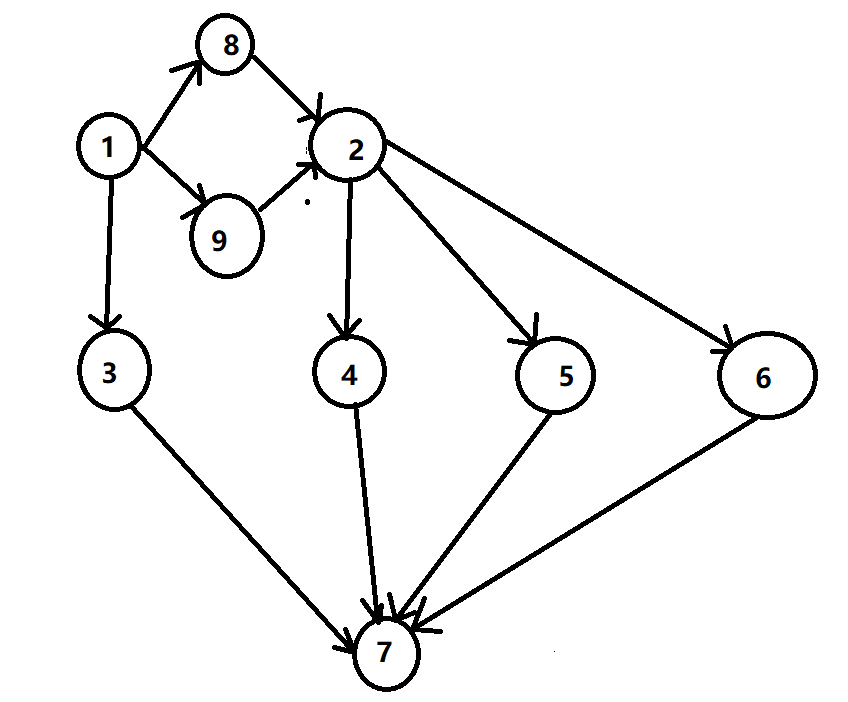
很显然,一共会有
$ 1 \rightarrow 3 \rightarrow 7 $
$ 1 \rightarrow 8 \rightarrow 2 \rightarrow 4 \rightarrow 7 $
$ 1\rightarrow 8 \rightarrow 2 \rightarrow 5 \rightarrow 7 $
$ 1 \rightarrow 8 \rightarrow 2 \rightarrow 6 \rightarrow 7 $
$ 1 \rightarrow 9 \rightarrow 2 \rightarrow 4 \rightarrow 7 $
$ 1\rightarrow 9 \rightarrow 2 \rightarrow 5 \rightarrow 7 $
$ 1 \rightarrow 9 \rightarrow 2 \rightarrow 6 \rightarrow 7 $
一共7条路径。排除起点和终点,我们发现,如果经过2号节点,有3条路径能够到达7号节点,如果暴力搜索,从1号经过8号到达2号时,会把2号为入口的三条路搜一遍,而经过9号到达2号时,也会把2号节点下属的三条路各搜一遍,这样就造成了时间的浪费。我们考虑,如果在经过8号节点到达2号节点,再到达终点7号节点的所有路径全部搜索完时,2号节点能够储存下“经过该节点有3条路径到达目标节点”这个信息,这样在从9号节点搜索到2号时,就不需要再重复地将接下来的路径全部搜索一遍了,直接从2号节点读到“接下来有3条不同的路径”这个信息。正好,DFS的“走到底再返回”的性质可以做到从尾到头,也就是从终点到起点记录信息,因此我们可以在DFS的过程中进行记忆化操作。
我们定义\(step[i]\)为“从\(i\)号节点到达目标节点的路径条数”,求解的目标是\(step[A]\),定义\(step[B]=1\),并且标记\(B\)节点已经被访问过。在DFS的过程中,如果将要搜索的节点没有被访问过,就搜索,并记录下路径条数,当前节点直接加上待搜索(其实这时候已经搜索完了)的节点的路径条数。以上图为例,DFS的过程如下:
- 初始化\(step[]\)数组为0,初始化\(vis[]\)数组为false,赋值\(step[7]=1,\enspace vis[7]=true\)。
- 从起点1开始DFS。接下来想搜索3,\(vis[3]==false\),进入。
- 从3节点开始DFS。接下来想搜索7,\(vis[7]==true\),不进入,累加路径条数\(step[3]=step[3]+step[7]\),这时\(step[3]=1\)。3节点没有其他的路径,赋值\(vis[3]=true\),返回。
- 对起点1而言,3节点搜索完毕,进行记录\(step[1]=step[1]+step[3]\),这时\(step[1]=1\)。
- 节点1开始仍然有路线,想搜索8,\(vis[8]==false\),进入。
- 从8节点开始DFS,接下来搜索2,进入,搜索4,进入,搜索7,\(vis[7]==true\),不进入,进行累加,\(step[4]=step[4]+step[7]=1\)。4节点无其他路径,搜索完成,\(vis[4]=true\),返回并累加,\(step[2]=step[2]+step[4]\),这时\(step[2]=1\)。
- 2节点仍未搜索完,搜索节点5,进入,搜索7,不进入,累加,\(step[5]=1\),搜索完成,\(vis[5]=true\),返回并累加,\(step[2]=step[2]+step[5]\),这时候\(step[2]=2\)。
- 2号节点仍有一条经过6的路径,类似地进行搜索,结束时\(step[2]=3\)。2节点搜索完毕,\(vis[2]=true\),返回并累加,\(step[8]=step[8]+step[2]\)。8节点搜索完毕,\(vis[8]=true, \enspace step[8]=3\),返回并累加,\(step[1]=step[1]+step[8]\)。这时\(step[1]=4\)。
- 接下来进入9号节点,想搜索2,但是此时\(vis[2]=true\),在之前的DFS过程中已经搜索过2了,这时就不进行搜索直接累加,\(step[9]=step[9]+step[2]=3\)(这里直接获取到了2号节点有3条不同路径这个信息)。9号节点搜索完毕,\(vis[9]=true\),直接返回并累加,\(step[1]=step[1]+step[9]\),此时\(step[1]=7\)。
- 起点搜索完毕,返回最终结果,\(step[1]=7\)即为最终答案。
上述过程用代码实现非常简单,如下:
void dfs(int r) {
vis[r] = true; //设置为已被访问。在搜索完设置与搜索前设置没有什么区别
for (int& i : fmp[r]) { //对于节点r的所有出边连接的直接后继
if (!vis[i]) dfs(i); //如果后继未被访问过,那么访问
step[r] += step[i]; //累加结果(如果访问过,那么就会有结果的记录)
}
}
当然我们可以在DFS过程中判断能否“逻辑自洽”。只要如下操作就行( ok 为bool 类型的全局变量并且初值为true):
void dfs(int r) {
vis[r] = true;
if (fmp[r].size() == 0 && r != b) { //如果出度为0并且不是目标终点
ok = false; //就记录为不“逻辑自洽”
}
for (int& i : fmp[r]) {
if (!vis[i]) dfs(i);
step[r] += step[i];
}
}
搜索过程中对每一个节点都只进行了一次访问,因此复杂度为\(O(n)\)。
代码实现
#include <bits/stdc++.h>
using namespace std;
#define FAST ios::sync_with_stdio(false);cin.tie(0);
#define rep(i,a,b) for(int i=a;i<=b;++i)
#define rrep(i,a,b) for(int i=a;i>=b;--i)
#define elif else if
#define mem(arr,val) memset(arr,val,sizeof(arr))
typedef long long ll;
typedef unsigned long long ull;
int n, m;
vector< vector<int> > fmp; //vector实现图的邻接表
vector<int> step;
vector<bool> vis;
int u, v, a, b;
bool ok;
void dfs(int r) {
vis[r] = true;
if (fmp[r].size() == 0 && r != b) {
ok = false;
}
for (int& i : fmp[r]) {
if (!vis[i]) dfs(i);
step[r] += step[i];
}
}
int main() {
FAST
cin >> n >> m;
fmp.resize(n + 1);
step.resize(n + 1, 0);
vis.resize(n + 1, false);
ok = true;
//以上为初始化
rep(i, 1, m) {
cin >> u >> v;
fmp[u].push_back(v);
}
cin >> a >> b;
step[b] = 1;
vis[b] = true;
dfs(a); //进行搜索
cout << step[a];
if (ok) {
cout << " Yes" << endl;
} else {
cout << " No" << endl;
}
return 0;
}
/*
_ _ _ _
/\ | | | | | | (_)
/ \ | | _____ _| |__| | ___ _ __ _ _ __ __ _
/ /\ \ | |/ _ \ \/ / __ |/ _ \| '__| | '_ \ / _` |
/ ____ \| | __/> <| | | | (_) | | | | | | | (_| |
/_/ \_\_|\___/_/\_\_| |_|\___/|_| |_|_| |_|\__, |
__/ |
|___/
*/
感谢你看到这里~


 浙公网安备 33010602011771号
浙公网安备 33010602011771号