树-下(堆)

堆

• 优先队列：特殊的队列，取出元素的顺序是依照元素的优先权大小，而不是元素进入队列的先后顺序。
• 采用数组或链表实现优先队列的时间复杂度

1. 数组：
      插入-元素总是插入尾部             O(1)
      删除-查找最大(最小)关键字         O(n)
            从数组中删除需要移动的元素  O(n)
2. 链表
      插入-元素总是插入链表的头部       O(1)
      删除-查找最大(最小)关键字        O(n)
            删去结点                  O(1)
3. 有序数组
      插入-找到合适的位置              O(n)或O(log2(n))
            移动元素并插入             O(n)
      删除-删去最后一个元素             O(1)
4. 有序链表
      插入-找到合适的位置               O(n)
            插入元素                   O(1)
      删除-删除首元素或最后元素          O(1)

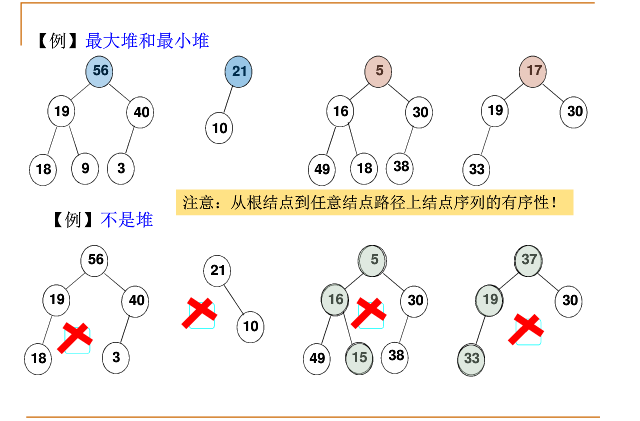
堆的两个特性

• 结构性：用数组表示的完全二叉树；
• 有序性：任一结点的关键字是其子树所有结点的最大值(最小值)
• 优先队列的完全二叉树表示
  
• 最大堆和最小堆示例
  

堆的抽象数据类型描述

类型名称：最大堆(MaxHeap)
数据对象集：完全二叉树，每个结点的元素值不小于其子结点的元素值
操作集：
1. MaxHeap Create(int MaxSize): 创建一个空的最大堆
2. Boolean IsFull(MaxHeap H): 判断最大堆H是否以满
3. Insert(MaxHeap H, ElementType item): 将元素item插入最大堆H
4. Boolean IsEmpty(Maxheap H): 判断最大堆H是否为空
5. ElementTyoe DeleteMax(MaxHeap H): 返回H中最大元素(高优先级)

最大堆的操作

1. 创建

typedef struct HeapStruct *MaxHeap;
struct HeapStruce {
      ElementType *Elements;
      int Size;
      int Capacity;
};

MaxHeap Create (int MaxSize) {
      MaxHeap H = malloc(sizeof(struct HeapStruct));
      H->Elements = malloc((MaxSize+1) * sizeof(ElementType));
      H->Size = 0;
      H->Capacity = MaxSize;
      H->Elements[0] = MaxData; //定义哨兵为最大堆中所有可能元素的值，便于以后更快操作
      return H;
}

2. 插入
   

• 将新增结点插入到从其父结点到根结点的有序序列中

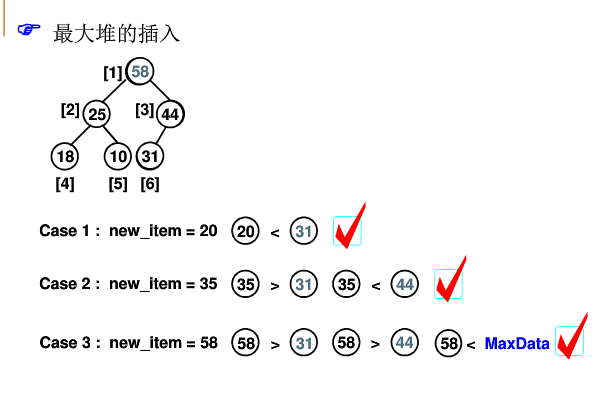
//O(log(N))
void Insert (MaxHeap H, ElementType item) {
      //将元素item插入最大堆H，其中H->Elements[0]已经定义为哨兵
      int i;
      if (IsFull(H)) {
            printf("最大堆已满");
            return ;
      }
      i = ++H->Size;           //i指向插入后堆中的最后一个元素的位置
      for ( ; H->Elements[i/2] < item; i/2)
            H->Elements[i] = H->Elements[i/2];  //向下过滤结点
      H->Elements[i] = item;                    //将item插入
}

3. 删除

• 取出根结点(最大值)元素，同时删除堆的一个结点

ElementType DeleteMax (MaxHeap H) {
//从最大堆H中取出键值为最大的元素，并删除一个结点
      int Parent, Child;
      ElementType MaxItem, temp;
      if (IsEmpty(H)) {
            printf("最大堆已为空");
            return ;
      }
      MaxItem = H->Elements[1]     //取出根结点最大值
      //用最大堆中最后一个元素从根结点开始向上过滤下层结点
      temp = H->Elemenets[H->Szie--];
      for (Parent = 1; Parent*2 <= H->Size; Parent = Child) {
            Child = Parent * 2;
            if (Chile != H->Size) && (H->Elements[Child] < H->Element[Child+1])
                  Child++;     //Child指向左右子结点的较大者
            if (temp >= H->Elements[Child])
                  break;
            else               //移动到temp元素到下一层
                  H->Elements[Patent] = H->Elements[Child];
      }
      H->Elements[Parent] = temp;
      return MaxItem;
}