本文目的
学习闫令琪老师的Games101课程的第六次作业过程中,不太理解getIntersection函数,因此查询资料学习如何判断射线是否与三角形相交。记录一下,原帖:https://www.ngui.cc/article/show-422266.html。
在计算机视觉中,经常需要判断一条射线是否与“三角形”相交。射线的起点o 是相机镜头O 在像平面的2D 点,射线的另外一点p 是“世界坐标系中的某个3D 点P 通过投影后在像平面上的2D 点”。“三角形”是3D 物体在像平面上“某个需求渲染表面的三角形小区域”。如果p 在三角形上,意味着相机可以看见3D 物体上的点P,该三角形需要被渲染。
那么,如何判断射线是否与三角形相交呢?本文就是来阐述该问题。
1、三角形ABC 内的点P 的性质
对于三角形ABC 内的任意一点P,学过线性代数和向量加法【两个向量相加等于两个向量组成的平行四边形的对角线向量】的就知道, 向量AP 、AB 、AC 线性相关。
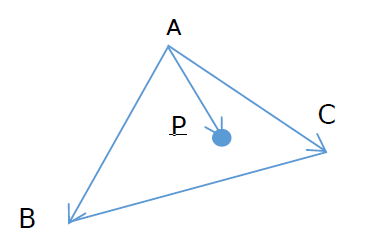
向量AP 、AB 、AC 线性相关且点P 在三角形ABC 之内,可以写为下面形式【P 在三角形内,意味这0 <= u, v <= 1, u+v <= 1 】:
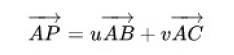
注意: 如果P 点不在三角形内, 那么是没法写为上面的向量相加的方程, 且满足0 <=u, v<= 1 和u+v <= 1 的约束条件的。线性相关,所以写成了线性组合的关系。
上面公式可以拆开写为:
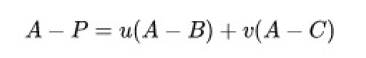
得到:
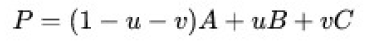
这也是点P 的表示方法:点P 可以表示为点A、B、C 分别乘以某个因子,然后相加。这里有约束条件: 0 <= u, v <= 1 且u+v <= 1 。
总结:如果点P 在三角形内,那么P 一定能写为P = (1 - u - v ) A + u B + v C 的形式。
重心坐标: 当把ABC 看成坐标系,始于A 点,基为: 向量AB 和向量AC 。这个坐标系叫做重心坐标系(barycentric,bary- 重的)。在重心坐标系中,有方程:
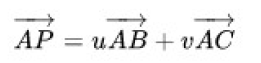
继续写:
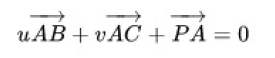

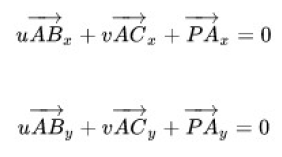
甚至我们还可以把它写成矩阵形式:

实际上,我们可以看作是在寻找向量(u, v, 1) 同时垂直于向量
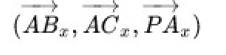
和向量
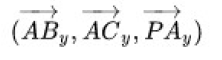
这不就是叉乘么?同时这给了我们一个有了P 点,求u 和v 的思路。
xvector = (B_x - A_x, C_x - A_x, A_x - P_x) yvector = (B_y - A_y, C_y - A_y, A_y - P_y) W = xvector 叉乘yvector ; 注意: 这里W 是向量[u, v, 1],W 在x- y- z 坐标系中的坐标值为[u, v, 1]
重点来了: 因为我们讨论的是二维的三角形, 如果W 的z 分量不等于1 则说明P 点不在三角形内。
因为我们的计算中涉及到浮点数,可能W 的z 分量不会一定等于1.0 。
令W 的三个分量是(a, b, c),我们代入原式子:
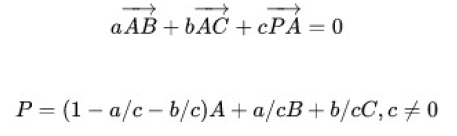
2、三角形Möller-Trumbore 算法(下文简称为M-T 算法)
Möller-Trumbore 算法的核心思想是一步到位的计算出光线是否与三角形相交,主要利用到的知识点是三角形的重心坐标。它是由Tomas Moller 和Ben Trumbore 于1997 年在一篇题名为“Fast, Minimum Storage Ray/Triangle Intersection”的论文中介绍。
传统的“求三角形与光线是否相交的算法”比较繁琐比较慢,而M-T 算法很直接很快。
2.1、传统求解射线是否与三角形相交的方法
首先看看用“循规蹈矩的笨方法”求一个三角形和光线相交的过程。
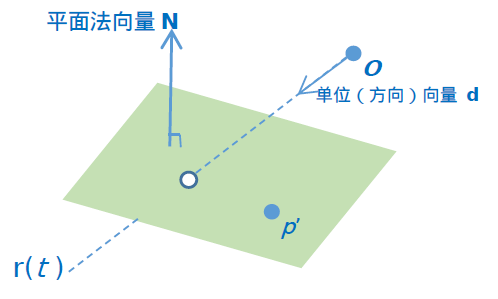
射线方程为: r ( t ) = O + t d , 0 ≤ t ≤∞ ; 这里的射线r ( t ) 其实是“有长度”其长度由t 决定, 射线的起点是O ,长度是“t 个单位向量d 的模长”。可以将t 理解为“时间或是尺度因子”。即:给定起点O ,方向向量d, 射线能射多远,就由t 决定。“射线是否与平面相交的问题,也就看看是否有一个具体的t1, 0 ≤ t 1 ≤∞ , 使得点p = r (t 1)在平面上。”
平面方程为: (p - p ’)·N = 0 , 即:给定一个法向量N, 平面上的任意向量(p - p’) 与N的内积等于0。也可以理解为:给定法向量N 和一点p ’, 那么满足(p -p ’)·N = 0 的任意点 p 就确定了一个平面,该平面过点p’,并且与向量N 垂直。
有了上面的射线方程和平面方程,那么,判断一条射线r (t )是否与平面相交的问题,就可以表示为对下面方程求解t ,如果t 在【0, +∞】内有解t1 ,那么就可以说射线r ( t )与平面相交。
假设p = r ( t ), 对下面方程求解t 。 把p理解成某个t时刻打到平面上的。
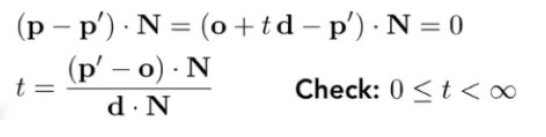
基于上面的分析,我们可以知道,传统上判断射线是否与三角形相交时,可以分为两步:
第一步: 判断射线是否与【三角形所在】平面相交。当光线r (t )与平面相交, 就有点p 满足(p - p ’)·N =0 , 同时p = o + t * d 。只有当(p - p ’)·N = 0 才能满足p 点在平面内。(p - p ’)这个向量垂直于法线方向。
第二步: 确定射线与平面相交后,再求得其交点p , 并判断该点是否在三角形内。
引出MT 算法:
有没有一种直接直接判断三角形是否与光线相交的方法呢?M-T 算法就是这个活的!
2.2、M-T 算法
我们已经知道,点P 可以写成三角形三个顶点乘上某个系数相加的形式:
P = a A + u B + v C; 其中1 <= a 且u, v >= 0 且a + u + v = 1
那么就可以写成:
o + t d = a A + u B + v C
由于a + u + v = 1 ,所以a = 1 - u - v ,所以,上式子可以继续写为:
o + t d = (1 - u - v ) A + u B + v C
=> o + t d = A - u A - v A + u B + v C
=> o + t d = A + (B - A)u + (C - A)v
=> o - A = -t d + (B-A) u + (C-A) v
这样就有了三个未知数t ,u ,v 和一个方程:
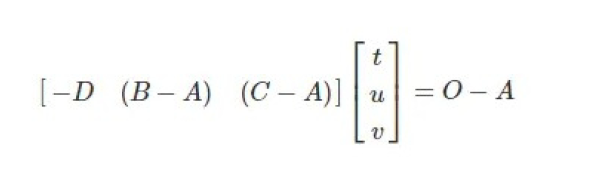
我们可以根据克莱姆法则(Cramer's rule)求解该问题,也就是:已知A、B、C,可以根据克莱姆法则得到D,然后根据上面方程求得t ,u ,v,如果t ,u ,v 满足下面条件,那么射线就与三角形相交。
条件1:求得的t 必须是一个大于0 的数。
条件2:求得的u 和v 必须是一非负的数且值小于等于1。
条件3:求得的v + u 必须是一个小于等于1 的数。
参考资料
https://docs.oakchina.cn/en/latest/
https://www.oakchina.cn/selection-guide/
https://www.ngui.cc/article/show-422266.html


 浙公网安备 33010602011771号
浙公网安备 33010602011771号