有趣计数题选做
1.[HEOI2013]SAO
题意实际上是让你求拓扑序数。
引用 \(\text{shaowice1984}\) 学长的一句话:“这题要是想拓扑图就凉了。”
我们可以先忽略边的限制直接建树,然后跑树形dp。
子树内的点对顺序到lca处统计贡献。
我们设 \(f[i][j]\) 表示 \(i\) 这个点处于拓扑序第 \(j\) 位的方案数。
那么对于 \(u\) 的子树 \(v\),如果 \(v\) 能放到 \(u\) 的前面,那么对 \(f[u][i+j]\) 的贡献有:
其中 \(v\in son_u\),我们枚举了 \(v\) 的子树有 \(j\) 个在 \(u\) 的前面。
那么更新后 \(u\) 前面的点有 \(i+j-1\) 个,我们选出了 \(i-1\) 属于 \(u\),那么这 \(i-1\) 个点排在 \(u\) 前面的方案是\(f[u][i]\)。
同理 \(u\) 的后面有 \(siz_u -i\) 个数。
那么我们可以通过限定 \(k\) 的范围来控制先后顺序,把 \(u\) 放在前面等价于 \(k\in[j+1,siz_v]\),我选的 \(k\) 在序列中一定大于 \(i+j-i\) 的位置。
同理,\(u\) 在后面就一定保证在小于等于 \(i+j-i\) 的位置。
发现最后一项可以前缀(后缀)和优化,复杂度 \(O(n^2)\) 。
2.[BJOI2012]最多的方案
不知道算不算计数,反正挺有意思的(
考虑斐波那契数列的增长速度很快,在 \(n\leqslant 10^{18}\) 时个数不会超过 \(100\) 。
那么我们可以先找出一个使用斐波那契数最少的方案,这个可以贪心实现。
可以证明,每种构造方案均是这个方案的子方案。
也就是说,可以对这个方案的斐波那契数进行拆分,构造其他方案。
我们设这个方案所用的斐波那契数下标为 \(\{a_1\dots a_m\}\),那么 \(\sum_{i=1}^mf_{a_i}=n\)。
设 \(dp_{i,0/1}\) 表示考虑到了 \(a_i\) ,即表示出了 \(\sum_{j=1}^if_{a_j}\) ,其中 \(f_{a_i}\) 有没有被分拆的方案总数。
如果不分拆,那么只考虑 \(i-1\) 即可。
那么转移有:
同理,分拆的话,需要用 \((a_{i-1},a_i)\) 或 \([a_{i-1},a_i)\) 间的数来凑出 \(a_i\)。
这其中任何一个数都可以在范围内被拆成两个数,边界要判断是否被拆。
我们发现每分拆一次范围里的数就会少 \(1\),再加上对边界的考虑,我们得到第一种情况的方案是 \(a_i-a_{i-1}-1\),第二种 \(a_i-a_{i-1}\)。
这样就可以转移了
3.[HAOI2012]道路
图上的简单计数。
首先要明确最短路图的概念:只有源点 \(S\) 和其与其他点的单源最短路形成的子图。
容易发现最短路图是无环的,在本题中是 \(dag\) 。
我们可以枚举每个点作为源点,跑出最短路。
那么一条边 \(u\rightarrow v\) 在这张图上的贡献可以如下统计:
其中 \(cnt\) 表示结束在某点的最短路数量,\(Cnt\) 表示从某点开始的最短路数。
前者可以在最短路图上拓扑排序求得。\(cnt_u=\sum_{u\in ver_v}cnt_v\)
后者可以利用拓扑序倒序推知。\(Cnt_u=\sum_{v\in ver_u}Cnt_v\)。
最后保证 \((u,v)\) 在最短路图上即可。
信仰跑 \(n\) 遍 \(SPFA\) 不会 \(TLE\)。
4.CF666C Codeword
\(\color{black}\text{s}\color{red}\text{hiroi}\) Orz。
显然,答案只与 \(|S|\) 有关,具有普适性。因此我们有一个 \(naive\) 的预处理dp做法。
设 \(f[i][j]\) 表示现在的串的前 \(j\) 位包含了 \(S\) 的前 \(i\) 位的方案数。
那么转移很显然,只要看当前位包不包含 \(S\) 的下一位即可。
这样做是 \(O(n^2)\) 的。仔细观察方程,发现它非常类似组合数的递推,或许我们可以想到更好的转移方式。
我们再考虑一下 \(f[i-1][j-1]\) 的实质:从前 \(j-1\) 位中选出 \(i-1\) 位填 \(S\) 中的字符,剩下的 “随便填”。
如果真的随便填的话,显而易见是会算重的,那么可以通过加一些约束来得到正确答案。
考虑重复的情况:当剩下的位“随便”填了 \(|S|\) 中的字符时,它在另一种方案中被选择。
思考匹配两个串的过程:对于两个相邻的 “匹配点”,我们钦定它们不能填后面那个 “匹配点” 的字符。
我们给这 \(\binom{j-1}{i-1}\) 种方案规定顺序:按匹配点从右向左排序。
这样,在匹配点左移的过程中,他所到的位置在之前的方案中并没有填它的字符,也就不会算重了。
所以 \(f[i-1][j-1]=\binom{j-1}{i-1}25^{j-i}\),我们找到了一种不依赖之前 \(i\) 来转移的方式。
这样下来,每个 \(i\) 之间是独立的,单次更新一个 \(i\) 是 \(O(n)\) 的。
题目保证 \(\sum|S|\leqslant 10^5\),那么不同的 \(|S|\) 只会有 \(\sqrt10^5\) 种。
直接暴力做就好,复杂度 \(O(n\sqrt n)\)。
5.CF1228E Another Filling the Grid
二项式反演。
我们设 \(g[i][j]\) 表示钦定 \(i\) 行 \(j\) 列不合法的方案数。
那么 \(g[i][j]=\binom n i\binom n j(k-1)^tk^{n^2-t}\)
其中 \(t\) 为不合法的格子数,二维前缀和有:\(t=n*i+n*j-i*j\)。
那么不合法的格子是不能填 \(1\) 的,有 \(k\) 种填法。同理剩下的有 \(k-1\) 种填法。
设 \(f[i][j]\) 表示恰好 \(i\) 行 \(j\) 列不合法的方案数。
则:
二项式反演,得:
我们的目标是 \(f[0][0]\),即 \(\sum_{x=i}^n\sum_{y=j}^n(-1)^{x+y}\binom x i\binom y jg[x][y]\)。
6.CF724F Uniformly Branched Trees
非常 有意思 的计数。
从重心考虑,钦定一棵树的重心为根,进行计数 \(dp\)。
这样子每棵子树的大小不超过 \(\frac n 2\),并且方便去重。
由于要考虑不同构的情况,所以我们按子树的大小从小向大计算。
我们设 \(f[i][j][k]\) 表示当前有 \(i\) 个节点的树,根节点的度为 \(j\),子树大小不超过 \(k\) 的方案数。
那么显然有转移:\(f[i][j][k]=f[i][j][k-1]\),不超过 \(k-1\) 的一定不超过 \(k\) 。
接下来我们就要考虑大小恰好为 \(k\) 的子树了。
枚举我们选了 \(t\) 棵大小为 \(k\) 的子树,那么剩下的方案数就是 \(f[i-tk][j-t][k-1]\),注意剩下的子树大小不能超过 \(k-1\)。
而这 \(t\) 棵树有不同的形态,我们知道大小为 \(k\),且合法的树的形态是 \(f[k][d-1][k-1]\)。
除去根节点,子树总大小为 \(k-1\),并且因为这棵树要作为子树,根节点的度有一条是连向 \(father\) 的。所以有 \(d-1\) 棵子树。
那么我们要从这么多种形态的树种选择 \(t\) 棵,同时这些树的形态可以重复,这就是一个可重组合,方案数为
在转移时还要乘上上面的组合数。
这样我们就处理完一个重心的问题了,但是还没有结束。因为当 \(n\) 为偶数时,可能这棵树有两个重心。
其他题解里对为什么会算重讲得不是很详细,这里我细说一下。
我们在考虑 树的同构 的时候,将子树的大小从小到大考虑,但这样真的考虑了所有情况吗?我们来看下面的图:
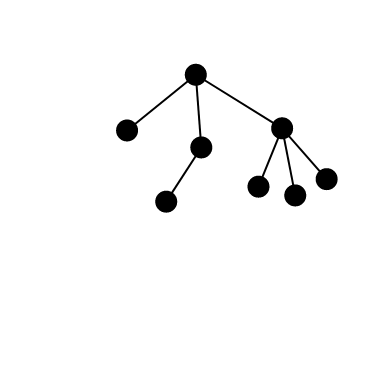
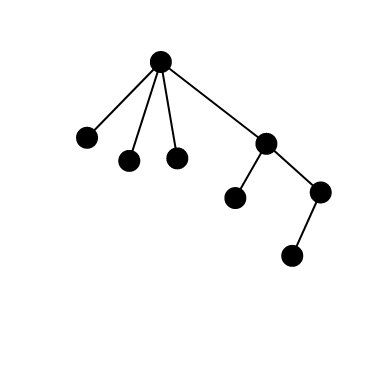
如上图,它们子树的大小的确是递增的,但是这两棵树却是同构的。
这是因为在两个重心分别当作根时,它与那些大小小于 \(\frac n 2\) 的子树共同成的树形态是不同的,即去掉重心之间连边形成的两棵树形态不同。这样就会被重复计数。
统计这种情况,可以将两个重心的连边看成点,它连接着两棵大小为 \(\frac n 2\) 的子树。
同上,大小为 \(\frac n 2\) 的树形态有 \(f[\frac n 2][d-1][\frac n2 -1]\) 种,我们要从这些形态里选出两种不重复的去重。
这样的方案数是:
统计答案时减掉就好了。
注意特判 \(n\leqslant2\) 的情况。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号