[HNOI2008]玩具装箱TOY

题目描述

P教授要去看奥运，但是他舍不下他的玩具，于是他决定把所有的玩具运到北京。他使用自己的压缩器进行压缩，其可以将任意物品变成一堆，再放到一种特殊的一维容器中。P教授有编号为1...N的N件玩具，第i件玩具经过压缩后变成一维长度为Ci.为了方便整理，P教授要求在一个一维容器中的玩具编号是连续的。同时如果一个一维容器中有多个玩具，那么两件玩具之间要加入一个单位长度的填充物，形式地说如果将第i件玩具到第j个玩具放到一个容器中，那么容器的长度将为 x=j-i+Sigma(Ck) i<=K<=j 制作容器的费用与容器的长度有关，根据教授研究，如果容器长度为x,其制作费用为(X-L)^2.其中L是一个常量。P教授不关心容器的数目，他可以制作出任意长度的容器，甚至超过L。但他希望费用最小.

输入输出格式

输入格式：

第一行输入两个整数N，L.接下来N行输入Ci.1<=N<=50000,1<=L,Ci<=10^7

输出格式：

输出最小费用

 

其实如果数据不大的话这个题挺简单的，但这个范围n^2肯定是过不了的，那怎么办呢，优化。推荐一篇论文：1D/1D动态规划优化；这里应用了决策单调性，就是类型1的解法；

状态转移方程式这样的：其中，可以O(1)计算w函数，这样算出来是n^2的时间复杂度；

通过简单的推算或证明，我们可以得出w函数满足决策单调性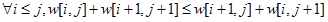，，那我们就可以按照套路进行优化；

用单调栈维护那些决策区间，每次决策从可能生效的那个决策区间二分，找到生效的那个点（在论文中称作“转折点”），然后修改这个决策区间和被二分的那个决策区间；

这样可以在最终的复杂度上加上一个log，变成O(nlogn)，这个题就可以过了；

下面上代码：

#include<iostream>
#include<cstdio>
#include<cmath>
#include<cstring>
#include<queue>
#include<set>
#include<algorithm>
#include<string>
#define ll long long
using namespace std;
const int inf=1e9;
const int MAXN=50005;
struct node{
    int l,r,p;
}q[MAXN];int n,L;
ll c[MAXN],f[MAXN],sum[MAXN];
int read(){
    int x=0,f=1;char ch=getchar();
    while(ch>'9'||ch<'0'){if(ch=='-') f=-f;ch=getchar();}
    while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();}
    return x*f;
}
ll sqr(ll x){return x*x;}
ll cal(ll j,ll i){return f[j]+sqr(sum[i]-sum[j]+i-j-1-L);}
int find(node t,int q){
    int l=t.l,r=t.r,mid;
    while(l<=r){
        int mid=(l+r)>>1;
        if(cal(q,mid)<cal(t.p,mid)) r=mid-1;
        else l=mid+1;
    } return l;
}
void dyna(){
    int h=1,t=0;
    q[++t]=(node){0,n,0};
    for(int i=1;i<=n;i++){
        if(i>q[h].r) h++;
        f[i]=cal(q[h].p,i);
        if(h>t||cal(i,n)<cal(q[t].p,n)){
            while(h<=t&&cal(i,q[t].l)<cal(q[t].p,q[t].l)) t--;
            if(h<=t){
                int tmp=find(q[t],i);
                q[t].r=tmp-1;
                q[++t]=(node){tmp,n,i};
            } else q[++t]=(node){i,n,i};
        }
    }
}
int main(){
    n=read();L=read();
    for(int i=1;i<=n;i++) c[i]=read();
    for(int i=1;i<=n;i++) sum[i]=sum[i-1]+c[i];
    dyna();printf("%lld\n",f[n]);return 0;
}