【二分图】特别接地气的讲解匈牙利算法

匈牙利算法是由匈牙利数学家Edmonds于1965年提出，因而得名。匈牙利算法是基于Hall定理中充分性证明的思想，它是部图匹配最常见的算法，该算法的核心就是寻找增广路径，它是一种用增广路径求二分图最大匹配的算法。

既然是解决二分图的最大匹配问题的算法，那么，就先来了解一下二分图是什么（来自度娘）：

二分图又称作二部图，是图论中的一种特殊模型。 设G=(V,E)是一个无向图，如果顶点V可分割为两个互不相交的子集(A,B)，并且图中的每条边（i，j）所关联的两个顶点i和j分别属于这两个不同的顶点集(i in A,j in B)，则称图G为一个二分图。

举个例子：下面就是一个二分图，我们可以发现，这个图上的顶点都被涂上了蓝（好像有点像紫色）或绿两种颜色，并且没有同色的相邻顶点，这种判断二分图的方法叫做染色法

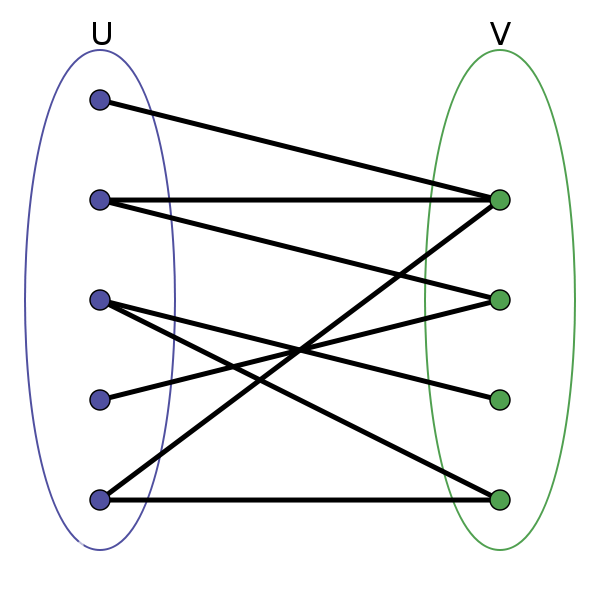
既然了解了二分图，那我们就可以开始学习匈牙利算法了。

但是，教科书上的专业语言真的让人很头大，要是看教科书，我可能这辈子都学不会匈牙利算法，但是我发现了一个很有趣的方法

假设你是一位光荣的新世纪媒人，在你的手上有N个剩男，M个剩女，每个人都可能对多名异性有好感，如果一对男女互有好感，那么你就可以把这一对撮合在一起，现在让我们无视掉所有的单相思，你拥有的大概就是下面这样一张关系图，每一条连线都表示互有好感。

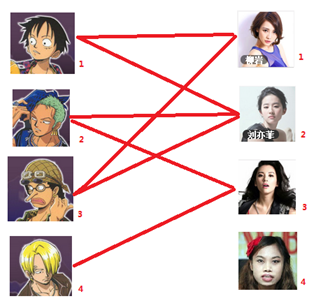
现在，你需要尽量多的撮合CP，用匈牙利算法，就是这样的：

一、先给1号男嘉宾找对象，你最先找到的便是1号女嘉宾，所以就先把他们连在一起

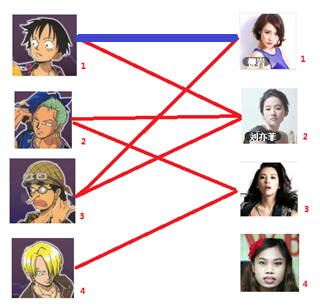
二、 接着，你要给2号男嘉宾找对象，就找到了2号女嘉宾，就把他们也连到一起

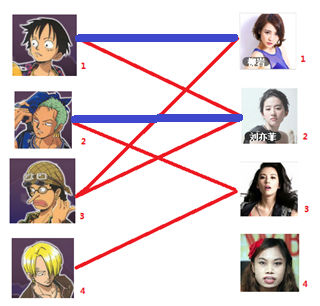
 三、接着，到了3号男嘉宾，可是1号女嘉宾已经名花有主了，那我们就尝试给1号男嘉宾另分配一个女嘉宾

 

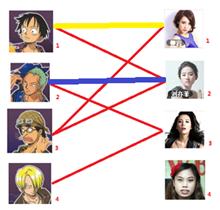
 与1号男嘉宾相连的第二个女生是2号女嘉宾，但是2号女嘉宾也有主了，我们再试着给2号男嘉宾重新找个妹子（同上）

 

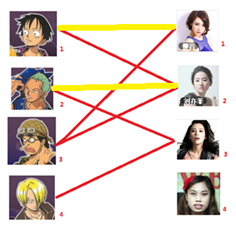
三、这个时候我们发现，2号男嘉宾还可以找3号女嘉宾，这样问题就解决了，我们就只需要：

 2号男嘉宾可以找3号女嘉宾                 1号男嘉宾可以找2号女嘉宾                3号男嘉宾可以找1号女嘉宾

 

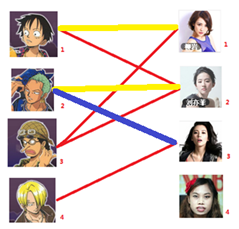
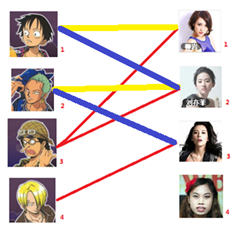
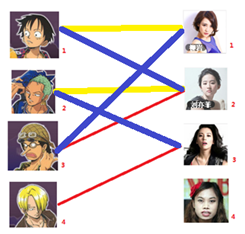
所以目前的结果就是这样：

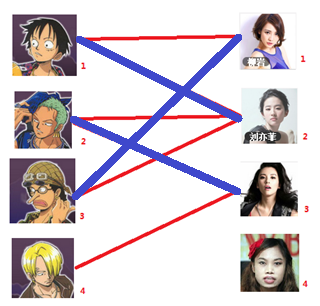
四、接下来是4号男嘉宾，很遗憾，按照第三步的方法我们没法给4号男嘉宾腾出来一个女嘉宾

 

所以匈牙利算法的基本原则便是:有机会就上，没机会创造机会也要上

模板如下：

bool dfs(int x){
    int i, j;
    for (j=1; j<=m; j++){                          //扫描每个妹子
        if (line[x][j] && !used[j]){               //如果有好感并且还没有标记过
            used[j]=1;
            if (girl[j] == 0 || dfs(girl[j])) { 　　//名花无主或者能腾出个位置来
                girl[j]=x;
                return true;
            }
        }
    }
    return false;
}

而主程序我们就只需要循环一下就好了：

for (i=1;i<=n;i++)
{
    memset(used,0,sizeof(used));    //在每一步中清空
    if （dfs(i)） ans+=1;
}