【有向图】强连通分量-Tarjan算法
好久没写博客了(都怪作业太多,绝对不是我玩的太嗨了)
所以今天要写的是一个高大上的东西:强连通
首先,是一些强连通相关的定义 //来自度娘
1.强连通图(Strongly Connected Graph)是指在有向图G中,如果对于每一对vi、vj,vi≠vj,从vi到vj和从vj到vi都存在路径,则称G是强连通图。
2.有向图的极大强连通子图,称为强连通分量(strongly connected components)。
当然,看定义是肯定看不懂的,所以,我举个栗子说明一下

我们以下图为例,这是一个特别经典的强连通图,三个被框起来的地方就分别是三个强连通分量
我们DFS一下,从一出发,我们从右至左遍历,所以路径便是1——>3——>5——>6,到了6,我们发现无路可走了,就回到5,而6不能到达任何一个点,所以它独自为一个强连通分量。同理,5也是一个强连通分量。而1——>3——>4——>1——>2,可以互相到达,所以这又是一个强连通分量。

Tarjan算法
接下来,就是一个在强连通中,常用的一个算法。
Tarjan算法是基于对图深度优先搜索的算法,每个强连通分量为搜索树中的一棵子树。搜索时,把当前搜索树中未处理的节点加入一个堆栈,回溯时可以判断栈顶到栈中的节点是否为一个强连通分量。
定义DFN(u)为节点u搜索的次序编号(时间戳),Low(u)为u或u的子树能够追溯到的最早的栈中节点的次序号。
当DFN(u)=Low(u)时,以u为根的搜索子树上所有节点是一个强连通分量。
接下来演示一下算法:
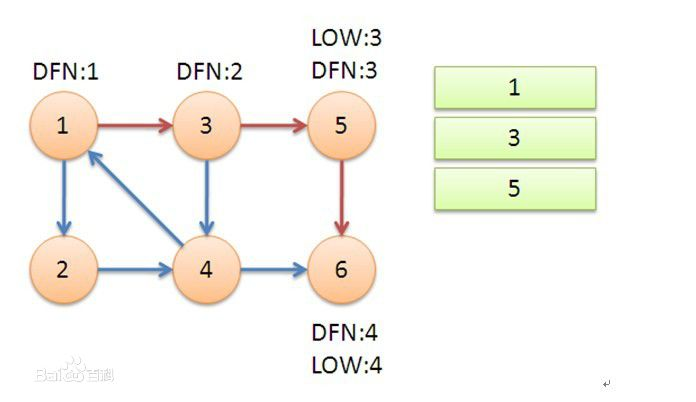
从1开始DFS,把遍历到的节点加入栈中。搜索到节点u=6时,DFN[6]=LOW[6],找到了一个强连通分量。退栈到u=v为止,{6}为一个强连通分量。

返回到5,发现DFN[5]=LOW[5],退栈后{5}为一个强连通分量。
继续回到1,最后访问2。访问边(2,4),4还在栈中,所以LOW[2]=DFN[4]=5。返回1后,发现DFN[1]=LOW[1],把栈中节点全部取出,组成一个连通分量{1,3,4,2}。
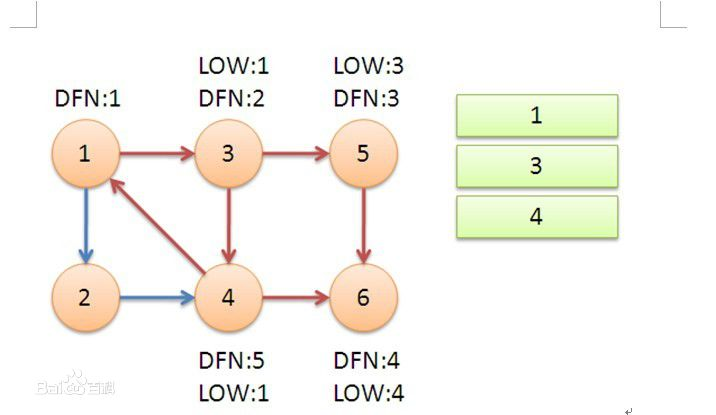
所以,三个强连通分量全部都找出来了。
模板如下:
1 void Tarjan(int u){ 2 dfn[u]=low[u]=++num; 3 st[++top]=u; 4 for (int i=fir[u]; i; i=nex[i]){ 5 int v=to[i]; 6 if (!dfn[v]){ 7 Tarjan(v); 8 low[u]=min(low[u],low[v]); 9 } 10 else if (!co[v]) 11 low[u]=min(low[u],dfn[v]); 12 } 13 if (low[u] == dfn[u]){ 14 co[u]=++col; 15 while (st[top]!=u){ 16 co[st[top]]=col; 17 --top; 18 } 19 --top; 20 } 21 }




