[***]HZOJ 跳房子
一道非常神仙的题.
算法一:对于20%的数据: 模拟,直接走K步,时间复杂度O(K)
算法二:对于40%的数据:走M*N步内必有一个循环节。直接走,找循环节,时间复杂度O(M*N)
正解大概有两种做法(我是第三种……)
1.利用分块思想,一行为一块。用一个数组记录第一列第i行走M步到达的位置jump[i]。在模拟过程中只要一行一行的走,不足一行再一步一步走,按行找循环节,时间复杂度O(M+N)。
更改操作:对于每个更改的单元格(x,y),我们回溯到第一列,找到第一列要更新的区间,更新jump[i] 。因为第一列到(x,y)的行是一个连续区间,在找的过程中,只需记录区间上下边界。复杂度为O(M+N)。
这个的查询比较容易,只是修改比较难搞,我研究了半天,证明了正确性和复杂度,又YY了一下代码实现,觉得细节太多代码又长想了想放弃了,目前xuefeng还在对拍中……这里只说一下修改:
结论1:如果第一列的点(i,1),(j,1)能到点(x,y),那么(i,1),(j,1)之间的点都会到(x,y),证明:路线不会交叉,自己YY一下就好啦。
于是设修改map[a][b]为e,那么对a,b左边的三个点分别向后搜索找到最后到的点,然后向前搜索找现在能到这这个点的一段,将这一段的jump都改为向后搜索找到的点。显然这三个点往前回溯找到的区间没有交叉两两之间没有间隙(因为路径不会交叉,手模一下就好啦),而之前能到(a,b)的点一定能到前面的三个点,所以修改(a,b)所影响的点都会考虑到,这样我们就证明了其正确性。然而在回溯时还有一个细节:如果对于每个点都向前分为三个点,那么时间复杂度无法保障,所以只能搜上下边界保证搜索的轨迹是两条线,但是这样对吗?大体是对的,不过有一个细节要考虑:
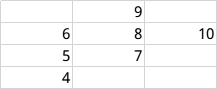
如图,设我们当前在处理10这个点,那么我们应该递归处理9和7而不会去处理8,但是这是7却不是最优的,显然走8才能找到下边界,所以要特判一种情况,当某个点无路可走时,跳的他上(下)面的点(有点难以理解,仔细想一下)。还有一个问题,这样搜索的点又会多不少,时间复杂度能保障吗?实际上是可以的,xuefeng开始觉得这样最坏是n×m的,但是仔细想想会发现,搜索的线路是一条折线,而这条折线的角度只能是45,于是复杂度最坏n+m。
还有一个细节要判断(我估计此时应该没人想打这个算法了……),就是三个点往前搜最后都无路可走的情况。
等旁边的xuefeng调完再放代码吧,不过和我讲的应该会有点(不少)出入……
(此处放代码)

1 #include<bits/stdc++.h> 2 #define N 2005 3 #define LL long long 4 #define Inf 0x3f3f3f3f 5 using namespace std; 6 int n,m,q,len,where_x,to_time; 7 int a[N][N],jump[N],vis[N]; 8 char s[10]; 9 int read(){ 10 int x=0,f=1;char ch=getchar(); 11 while(!isdigit(ch))f=(ch=='-')?-1:1,ch=getchar(); 12 while(isdigit(ch))x=x*10+ch-'0',ch=getchar(); 13 return x*f; 14 } 15 inline int _x(int x){ 16 return (x+n*2-1)%n+1; 17 } 18 inline int _y(int y){ 19 return (y+m*2-1)%m+1; 20 } 21 void get(int &x,int &y){//真 22 y=_y(y+1);x=_x(x); 23 int imax=x,xu=_x(x-1),xd=_x(x+1); 24 if(a[imax][y]<a[xu][y])imax=xu; 25 if(a[imax][y]<a[xd][y])imax=xd; 26 x=imax; 27 } 28 void _get(int &x,int y){//假 29 y=_y(y+1); 30 int imax=x,xu=_x(x-1),xd=_x(x+1); 31 if(a[_x(imax)][y]<a[xu][y])imax=x-1; 32 if(a[_x(imax)][y]<a[xd][y])imax=x+1; 33 x=imax; 34 } 35 36 void work(int l,int r){ 37 for(int i=l;i<=r;++i){ 38 int pos=i;int j=1; 39 do get(pos,j); 40 while(j!=1); 41 jump[i]=pos; 42 } 43 } 44 int L[N],R[N]; 45 void work_for(pair<int,int>x){ 46 L[x.second]=R[x.second]=x.first; 47 for(int i=x.second;i>=2;--i){ 48 if(L[i]>R[i])return;L[i-1]=Inf;R[i-1]=-Inf; 49 int e1=L[i]-1,e2=L[i],e3=L[i]+1; 50 _get(e1,i-1),_get(e2,i-1),_get(e3,i-1); 51 if(e1>=L[i]&&e1<=R[i])L[i-1]=L[i]-1; 52 else if(e2>=L[i]&&e2<=R[i])L[i-1]=L[i]; 53 else if(e3>=L[i]&&e3<=R[i])L[i-1]=L[i]+1; 54 55 e1=R[i]-1,e2=R[i],e3=R[i]+1; 56 _get(e1,i-1),_get(e2,i-1),_get(e3,i-1); 57 if(e3>=L[i]&&e3<=R[i])R[i-1]=R[i]+1; 58 else if(e2>=L[i]&&e2<=R[i])R[i-1]=R[i]; 59 else if(e1>=L[i]&&e1<=R[i])R[i-1]=R[i]-1; 60 } 61 pair<int,int>x1=x; 62 do get(x1.first,x1.second); 63 while(x1.second!=1); 64 for(int i=L[1];i<=R[1];++i)jump[_x(i)]=x1.first; 65 } 66 void Work(int x,int y){ 67 pair<int,int>e1,e2,e3; 68 e1.first=_x(x-1),e1.second=_y(y-1); 69 e2.first=x,e2.second=_y(y-1); 70 e3.first=_x(x+1),e3.second=_y(y-1); 71 work_for(e1);work_for(e2);work_for(e3); 72 } 73 void get_tarjan(int row){ 74 memset(vis,-1,sizeof vis); 75 for(int i=0;i<=n+2;++i){//花多少k到达 76 if(vis[row]!=-1){ 77 len=i-vis[row];//环长 78 where_x=row;//环开始的地方 79 to_time=vis[row];//开始时间 80 return; 81 } 82 vis[row]=i; 83 row=jump[row]; 84 } 85 } 86 int main(){ 87 //freopen("text.in","r",stdin); 88 //freopen("a.out","w",stdout); 89 scanf("%d%d",&n,&m); 90 for(int i=1;i<=n;++i)for(int j=1;j<=m;++j)scanf("%d",&a[i][j]); 91 work(1,n); 92 scanf("%d",&q); 93 int k,aa,b,e; 94 int row=1,col=1; 95 for(int i=1;i<=q;++i){ 96 scanf("%s",s); 97 if(s[0]=='m'){ 98 scanf("%d",&k); 99 while(col!=1&&k){k--;get(row,col);} 100 if(k>m){ 101 get_tarjan(row); 102 if(k>to_time*m){ 103 k-=to_time*m; 104 row=where_x; 105 k%=len*m; 106 } 107 } 108 while(col!=1&&k){k--;get(row,col);} 109 while(k>=m){k-=m;row=jump[row];} 110 while(k){k--;get(row,col);} 111 printf("%d %d\n",row,col); 112 } 113 else{ 114 scanf("%d%d%d",&aa,&b,&e);aa=_x(aa);b=_y(b);a[aa][b]=e; 115 Work(aa,b); 116 } 117 } 118 } 119 /* 120 3 6 121 204 889 21 921 229 601 122 465 187 937 481 241 147 123 882 201 8,581 301 457 829 124 20 125 change 126 3 3 581 127 change 128 1 1 951 129 move 130 46003169 131 move 132 93518379 133 move 134 44247980 135 move 136 20045342 137 change 138 1 1 661 139 move 140 37489600 141 move 142 95847680 143 move 144 74183070 145 move 146 290360 147 change 148 2 1 233 149 move 150 24935765 151 change 152 1 5 924 153 move 154 91540280 155 change 156 3 1 790 157 change 158 3 3 845 159 move 160 50868396 161 move 162 69816331 163 move 164 18735250 165 */ 166 /* 167 3 6 168 951 889 21 921 229 601 169 465 187 937 481 241 147 170 882 201 581 301 457 829 171 20 172 move 173 20045342 174 */ 175 /* 176 3 6 177 2 3 178 3 5 179 3 1 180 3 5 181 3 1 182 3 1 183 2 3 184 1 2 185 1 4 186 1 4 187 1 5 188 2 3 189 */
2.可以发现每走一步相当于一次置换,所以可以用线段树维护置换,置换满足结合律,查询可以使用快速幂,而修改只需要修改线段树的一条链。这个我也没打,具体看ex_face的blog
3.我自己YY的跑的超慢但是A掉的算法(其实是因为懒第一种不想打,笨第二种看不懂)。
题解中运用了循环节的思想,目的是将k模掉来降低复杂度,但是这样复杂度取决与循环节长度比较不稳定,那怎么办呢?可以沿用题解中jump数组的做法,而使用倍增,求出第一列每个点走$2^j*m$步到达的点,这样查询就是logk的,那修改呢?重新求倍增数组那个$n*log_m$是跑不了了,但是这样的复杂度是可以接受的,但是jump数组怎么搞呢?暴力m*n求的话肯定会死,所以沿用第二种做法中线段树的思想,每个节点维护一个jump数组,叶子节点jump[j]表示这列第j行走1步到达的行数,那么叶子节点的父亲就表示左边l列走2步到达的行数,上面的节点也一样,那么对于每次修改,我们对其对应的叶子节点Om暴力修改,然后递归处理一条链,总复杂度$n*log_m$,之后重新求倍增数组,总复杂度可以接受。

1 #include<iostream> 2 #include<cstdio> 3 #define LL long long 4 #define MAXN 2010 5 #define int LL 6 #define lo 30 7 #define re register 8 using namespace std; 9 int n,m,Q; 10 struct jum 11 { 12 int jump[MAXN]; 13 void init() 14 {for(int i=1;i<=n;i++)jump[i]=i;} 15 }tmp; 16 void move(re int &x,re int &y); 17 void mul(jum &a,jum &b,jum &c) 18 {for(int i=1;i<=n;i++)c.jump[i]=b.jump[a.jump[i]];} 19 struct tree 20 { 21 jum j; 22 int l,r; 23 #define l(x) tr[x].l 24 #define r(x) tr[x].r 25 #define ls(x) (x<<1) 26 #define rs(x) (ls(x)+1) 27 #define j(x) tr[x].j 28 }tr[MAXN*10]; 29 void build(int x,int l,int r) 30 { 31 l(x)=l,r(x)=r; 32 if(l==r) 33 { 34 int tem=l; 35 for(int i=1;i<=n;i++)move(j(x).jump[i]=i,tem=l); 36 return; 37 } 38 int mid=(l+r)>>1; 39 build(ls(x),l,mid); 40 build(rs(x),mid+1,r); 41 mul(j(ls(x)),j(rs(x)),j(x)); 42 } 43 void add(int x,int t) 44 { 45 if(l(x)==r(x)) 46 { 47 int tem=t; 48 for(int i=1;i<=n;i++)move(j(x).jump[i]=i,tem=t); 49 return; 50 } 51 int mid=(l(x)+r(x))>>1; 52 if(t<=mid)add(ls(x),t); 53 else add(rs(x),t); 54 mul(j(ls(x)),j(rs(x)),j(x)); 55 } 56 int nowi=1,nowj=1; 57 int map[MAXN][MAXN]; 58 char op[10];int x,a,b,e; 59 int ju[MAXN][lo+5]; 60 inline int read(); 61 signed main() 62 { 63 // freopen("jump4.in","r",stdin); 64 65 n=read(),m=read(); 66 for(int i=1;i<=n;i++) 67 for(int j=1;j<=m;j++) 68 map[i][j]=read(); 69 70 Q=read(); 71 build(1,1,m); 72 for(int i=1;i<=n;i++) 73 ju[i][0]=j(1).jump[i]; 74 for(re int i=1;i<=lo;i++) 75 for(int j=1;j<=n;j++) 76 ju[j][i]=ju[ju[j][i-1]][i-1]; 77 for(int i=1;i<=Q;i++) 78 { 79 scanf("%s",op); 80 if(op[0]=='m') 81 { 82 x=read(); 83 while(nowj!=1&&x){move(nowi,nowj),x--;} 84 for(int k=lo;k>=0;k--) 85 if(1ll*(1<<k)*m<=x) 86 {nowi=ju[nowi][k],x-=1ll*(1<<k)*m;} 87 while(x){move(nowi,nowj),x--;} 88 printf("%lld %lld\n",nowi,nowj); 89 } 90 else 91 { 92 a=read(),b=read(),e=read(); 93 map[a][b]=e; 94 if(b==1)add(1,m); 95 else add(1,b-1); 96 for(int j=1;j<=n;j++) 97 ju[j][0]=j(1).jump[j]; 98 for(re int j=1;j<=lo;j++) 99 for(int k=1;k<=n;k++) 100 ju[k][j]=ju[ju[k][j-1]][j-1]; 101 } 102 } 103 } 104 inline int read() 105 { 106 int s=0;char a=getchar(); 107 while(a<'0'||a>'9')a=getchar(); 108 while(a>='0'&&a<='9'){s=s*10+a-'0',a=getchar();} 109 return s; 110 } 111 void move(re int &x,re int &y) 112 { 113 int t1,t2,t3; 114 if(y!=m) 115 { 116 t1=(x==1?map[n][y+1]:map[x-1][y+1]), 117 t2=map[x][y+1], 118 t3=(x==n?map[1][y+1]:map[x+1][y+1]); 119 } 120 else 121 { 122 t1=(x==1?map[n][1]:map[x-1][1]), 123 t2=map[x][1], 124 t3=(x==n?map[1][1]:map[x+1][1]); 125 } 126 if(t1>t2&&t1>t3) x--,y++; 127 else if(t2>t1&&t2>t3)y++; 128 else x++,y++; 129 if(x==0)x=n; 130 if(x==n+1)x=1; 131 if(y==0)y=m; 132 if(y==m+1)y=1; 133 }
最后,附赠xuefeng的玄学乱搞骗到85分(不知道为啥我只能搞到80)的思路(以下纯属乱搞):
首先是20分的暴力一步一步地模拟(这个应该都会打吧),然后在输入k后加一句话:if(k>10*m)k%=10*m,k+=2*m;看似很选学,实际上是有点依据的,首先循环节肯定是m的整数倍,那为什么选10呢?借用wq学长的话:小了会WA大了会T。那加2*m又是为啥呢?因为在碰到循环节之前会走一个常数。

1 #include<bits/stdc++.h> 2 #define N 2005 3 #define LL long long 4 using namespace std; 5 int n,m,q; 6 int a[N][N]; 7 char s[6]; 8 inline int read(){ 9 LL x=0,f=1;char ch=getchar(); 10 while(!isdigit(ch))f=ch=='-'?-1:1,ch=getchar(); 11 while(isdigit(ch))x=x*10+ch-'0',ch=getchar(); 12 return x*f; 13 } 14 void get(int &x,int &y){ 15 y=y+1==m+1?1:y+1;int xu=x-1==0?n:x-1,xd=x+1==n+1?1:x+1; 16 if(a[x][y]<a[xu][y])x=xu;if(a[x][y]<a[xd][y])x=xd; 17 } 18 int main(){ 19 n=read(),m=read(); 20 for(int i=1;i<=n;++i)for(int j=1;j<=m;++j)a[i][j]=read(); 21 q=read();int k,A,b,e; 22 int row=1,col=1; 23 for(int i=1;i<=q;++i){ 24 scanf("%s",s); 25 if(s[0]=='m'){ 26 k=read(); 27 if(k>m*10)k%=m*10,k+=m*2; 28 while(k--)get(row,col); 29 printf("%d %d\n",row,col); 30 } 31 else{ 32 A=read(),b=read(),e=read(); 33 a[A][b]=e; 34 } 35 } 36 }



 ヾ(≧O≦)〃嗷~
ヾ(≧O≦)〃嗷~